Kinetic Model of an Ideal Gases Definition of

































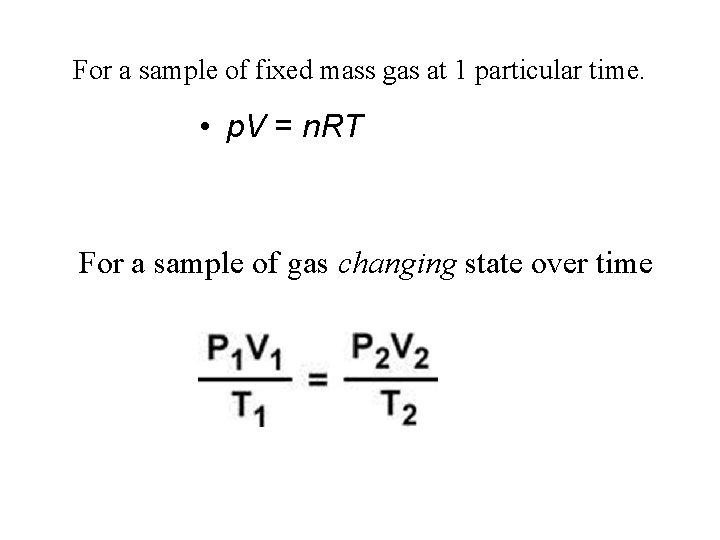
























- Slides: 72

Kinetic Model of an Ideal Gases Definition of Properties Pressure Volume

Ideal Gasses A state of matter where particles are so separated, that intermolecular forces are almost negligible. Particles have a higher kinetic energy than liquid, or solid. Not so much bond E.

Develop Assumptions from PHET Sim

Kinetic Model Ideal Gas Assumptions 1) Molecules are spheres 2) Molecules identical 3) Perfectly elastic collisions (no loss KE). 4) No intermolecular forces – constant v between collisions – straight line. 5) No molecular volume. 6) Follow Ideal Gas Law PV = n. RT.

Ideal Gasses Obey ideal Gas Law • PV = n. RT • • • P Pressure Pascals V in m 3. n – number of moles. R – gas constant 8. 31 J/K mol. T – Kelvin.

Pressure molecule in box • • • Is there acceleration? Fnet on molecule? By N 3 Walls of box P by N 3

Gas Molecules Exert Pressure on Container • There are collisions between gas molecules & the container walls. • Pressure due to Dp or impulse of particle = Ft when they bounce & changes p. (contact time considered instantaneous).

The Dp (m. Dv) causes an impulse on walls. F or P = Dp/t is a collision rate. Low P, less force (KE), lower collision rate. High P, more force (KE), higher collision rate.

Pressure • Force/Area. • Pascal = N/m 2. • 1 Atm = 101 k. Pa • So if you have 1 m 2 window, it has 101, 000 N pressing on it.

1: A 360 N child sits on a stool which weighs 41 N. The bottom of the stools legs touch the ground over an area of 19. 3 cm 2: Calculate the pressure in Pa. • 401 N/ 1. 93 x 10 -3 m 2 • 2. 1 x 105 Pa

2. A 150 -kg man stands on one foot on some ice. Given that his foot is about 9. 0 cm by 10. cm in rectangular cross-section, find the pressure on the ice. • • F = mg = 150(10) = 1500 N. Then find the area: A = LW = (. 09)(. 10) = 0. 009 m 2. p = F / A = 1500 /. 009 = 170000 N m-2 = 170000 Pa.

3. If the ice is thin enough that it will break under a pressure of 1. 0 105 Pa, what should be the area of a snowshoe that will just prevent him from breaking through when on one foot? • A=F/p= • 1500 / 100000 • 0. 015 m 2.

Kinetic Model of Gasses • Pressure, Volume, Temperature Relationships. • Pressure – force of collisions, rate of collisions, number of collisions.

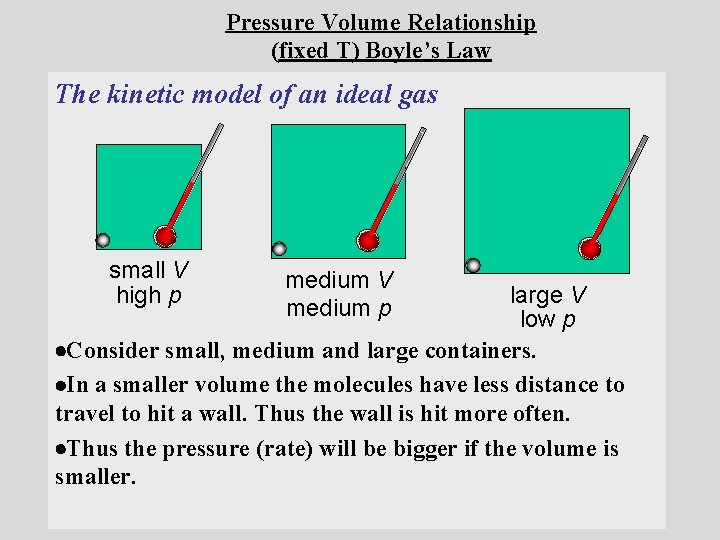
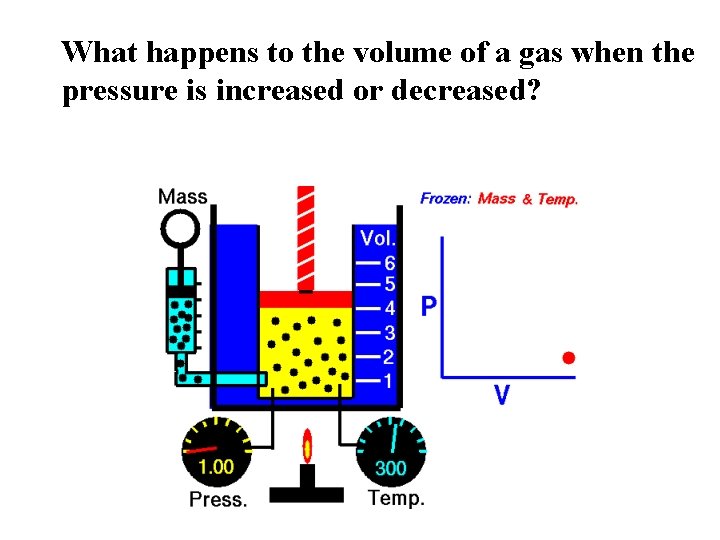
Pressure Volume Relationship (fixed T) Boyle’s Law The kinetic model of an ideal gas small V high p medium V medium p large V low p Consider small, medium and large containers. In a smaller volume the molecules have less distance to travel to hit a wall. Thus the wall is hit more often. Thus the pressure (rate) will be bigger if the volume is smaller.

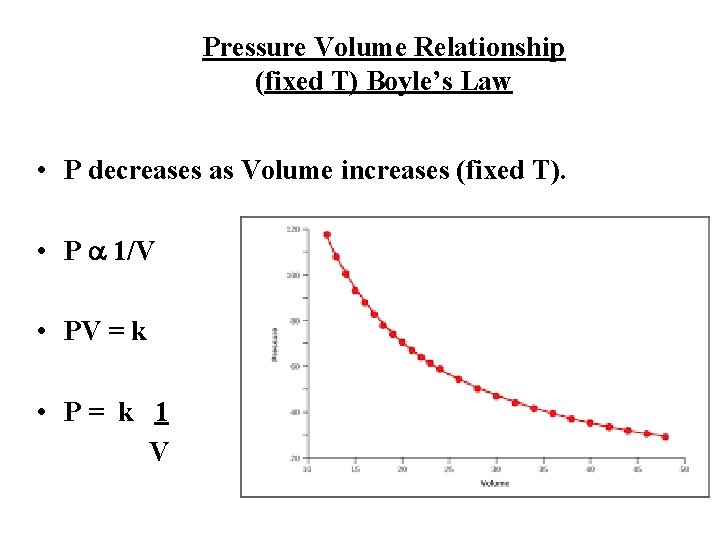
Pressure Volume Relationship (fixed T) Boyle’s Law • P decreases as Volume increases (fixed T). • P a 1/V • PV = k • P= k 1 V

Pressure Temperature Relationship fixed volume • As T goes up - molecular KE goes up. • Frequency of collisions go up. • Dp increases with increase Dv. Impulse Ft on wall increases.

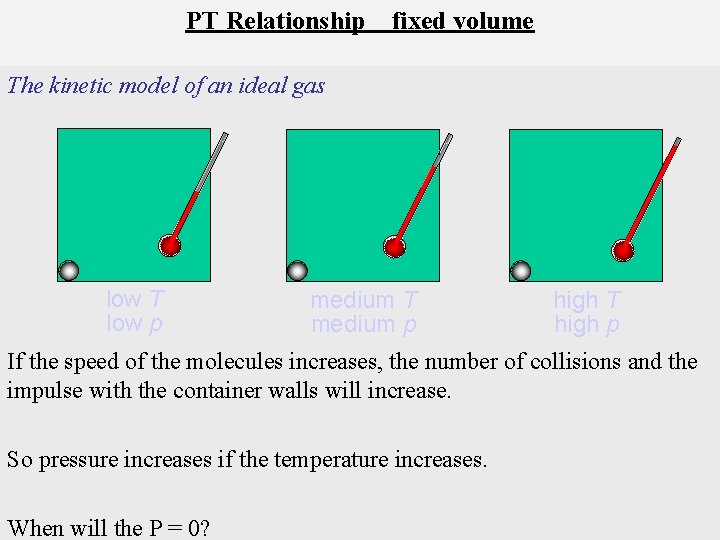
PT Relationship fixed volume The kinetic model of an ideal gas low T low p medium T medium p high T high p If the speed of the molecules increases, the number of collisions and the impulse with the container walls will increase. So pressure increases if the temperature increases. When will the P = 0?

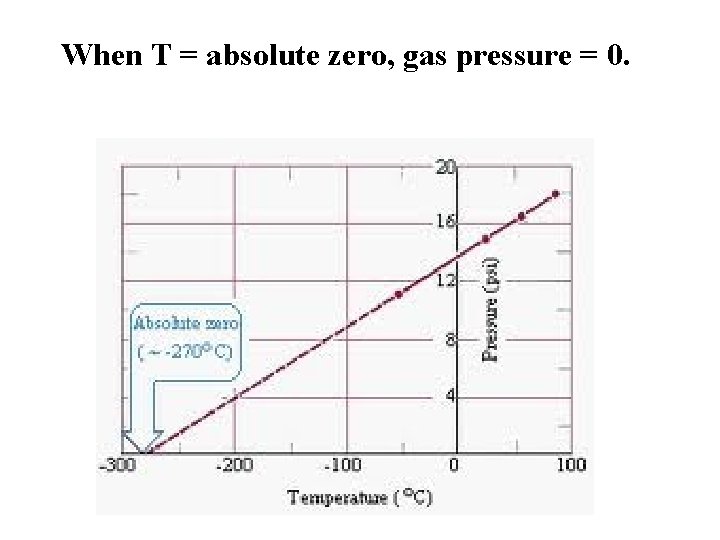
When T = absolute zero, gas pressure = 0.

Charles’ Law Temp Volume fixed pressure

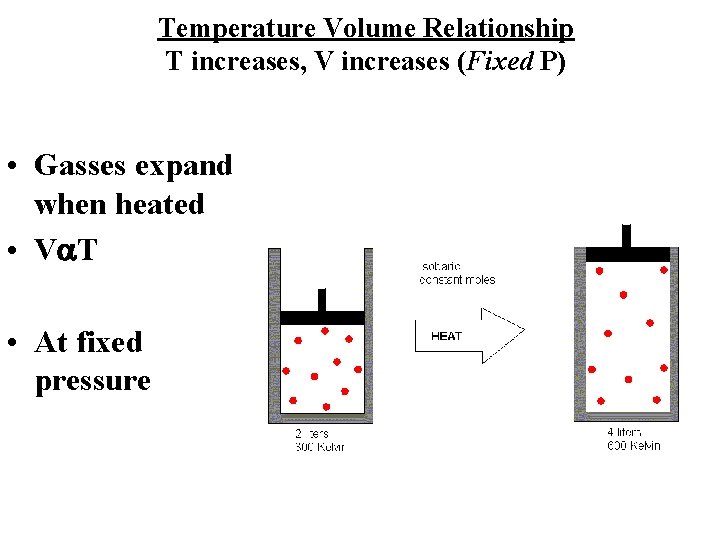
Temperature Volume Relationship T increases, V increases (Fixed P) • Gasses expand when heated • Va. T • At fixed pressure

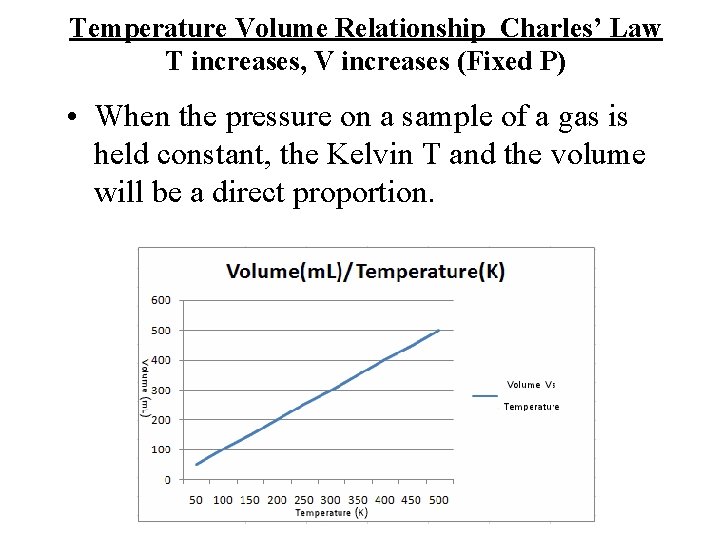
Temperature Volume Relationship Charles’ Law T increases, V increases (Fixed P) • When the pressure on a sample of a gas is held constant, the Kelvin T and the volume will be a direct proportion.

Work done

Work done on or by a gas and DT vary P Consider a syringe full of an ideal gas. If we make the volume less, the T will increase. The plunger exerts a force on the gas & displaces molecules, it does work on the gas. From the work-KE theorem - do work on the gas, its KE must increase. Its speed increases, its T increases. If the process is reversed the gas will do work, lose EK and cool.

KE Model and T Visualize • When you push the piston in to reduce the volume, some molecules are swatted giving them KE. Work is done on gas. • When a gas pushes the piston out, increasing the volume, it does work & the KE of the gas goes down.

Example IB Problem Temperature is a measure of the EK of the gas. Reducing the EK reduces the frequency of collisions.

Changing conditions over time For the same amount of gas molecules changing its condition the following holds true: 4. Calculate the % change in volume of a fixed mass of ideal gas when its pressure is increased by a factor of 2, and its T increases from 30 – 120 o. C. Use Kelvin Temp’s.

• Find ratio V 2/V 1. • 65 %

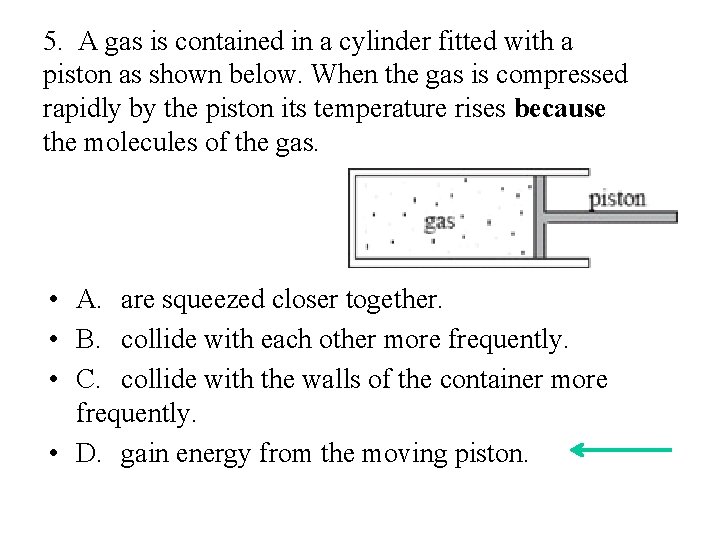
5. A gas is contained in a cylinder fitted with a piston as shown below. When the gas is compressed rapidly by the piston its temperature rises because the molecules of the gas. • A. are squeezed closer together. • B. collide with each other more frequently. • C. collide with the walls of the container more frequently. • D. gain energy from the moving piston.

How do we account for the mass or the amount of substance present?

• Hwk: Read Hamper (purple) pg 62 – 66. Be prepared to take a quick quiz on the reading tomorrow.

Avogadro’s number NA : Equal volumes of gas at STP have equal #of molecules. Mole is an amount. At STP 1 mol has Avogadro’s number NA of particles (atoms or molecules). NA = 6. 02 x 1023 molc/mol.

The mole and molar mass Recall from the periodic table of the elements that each element has certain weights associated with it (u). We define the mole of a homogeneous substance as follows: 1 mole is the number of atoms of an element that will have a mass in grams equal to its atomic weight.

EXAMPLE: Find the mass (in kg) of one mole of carbon. SOLUTION: From the periodic table we see that it is just 1 mole C = 12. 011 grams = 0. 012011 kg.

The mole and molar mass – not on sheet PRACTICE Not on sheet: What is the molar mass of oxygen? SOLUTION: It is 15. 9994 g, or if you prefer, (15. 9994 g)(1 kg / 1000 g) = 0. 015994 kg. PRACTICE: What is the molar mass of phosphorus in From the periodic table we see that the molar mass of phosphorus is grams. The molar mass in kilograms is 0. 030973762 kg. kilograms? 30. 973762

The mole and molar mass 7: Water is made up of 2 hydrogen atoms and 1 oxygen atom and has a molecular formula given by H 2 O. Find (a) the molar mass of water. . (b) how many moles of hydrogen and oxygen there are in 1 mole of water. SOLUTION: (a) H 2 O is 2(1. 0) + 1(16. 0) = 18. 0 g per mole. Thus the mass of 1 mole of H 2 O is 18. 01528 g. (b) Since each mole of H 2 O has 2 H and 1 O, there are 2 moles of H and 1 mole of O for each mole of water.

Topic 3: Thermal physics 3. 2 – Modeling a gas The mole and molar mass 7: Suppose we have 12. 25 g of water in a Dixie. TM Cup? How many moles of water does this amount to? SOLUTION: We determined that H 2 O is 18. 01528 g per mole. Thus (12. 25 g)(1 mol / 18. 01528 g) = 0. 6800 mol. FYI significant figures!

The Avogadro constant A mole of any substance has 6. 02 1023 particles. NA = 6. 02 1023 molecules. the Avogadro constant 8: How many atoms of P are there in 31. 0 g of it? SOLUTION: There are NA = 6. 02 1023 atoms of P in 31. 0 g of it.

Topic 3: Thermal physics 3. 2 – Modeling a gas The Avogadro constant NA = 6. 02 1023 molecules. the Avogadro constant To find the number of atoms in a sample, convert to moles, 1 mol = 6. 02 1023 molecules. 8. How many P atoms of P are there in 145. 8 g of it? SOLUTION: Start with the given: (145. 8 g)(1 mol / 30. 984 g)(6. 02 1023 atoms / 1 mol) = 2. 83 1024 atoms of P.

9: A sample of carbon has 1. 28 1024 atoms as counted by Marvin the Paranoid Android. C = 12. 011 u. a) How many moles is this? b) What is its mass in grams? SOLUTION: a) (1. 28 1024 atoms)(1 mol / 6. 02 1023 atoms) = 2. 13 mol. b) (2. 13 mol)(12. 011 g / mol) = 25. 5 g of C.

Topic 3: Thermal physics Equation of state for an ideal gas Ideal Gas Law. p. V = n. RT R = 8. 31 J / mol·K is the universal gas constant equation of state of an ideal gas p (pressure), V (volume), n (number of moles), and T (temperature) are called the 4 state variables. p is measured in Pascals or Nm-2. V is measured in m 3. T is measured in K. n = moles
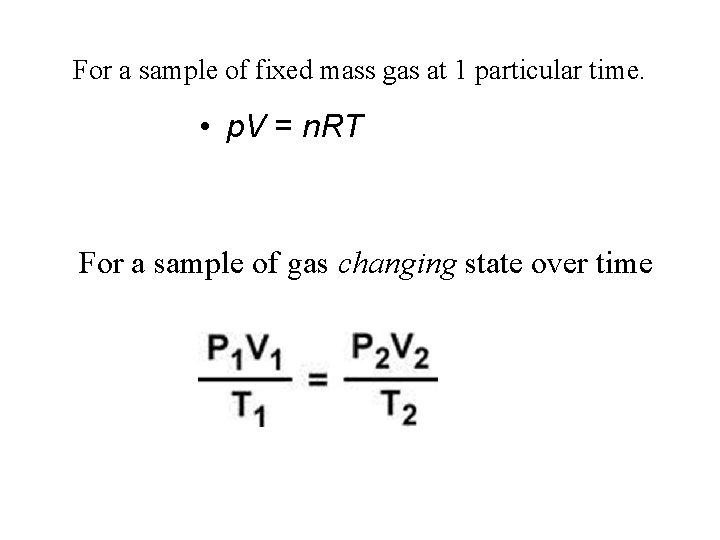
For a sample of fixed mass gas at 1 particular time. • p. V = n. RT For a sample of gas changing state over time

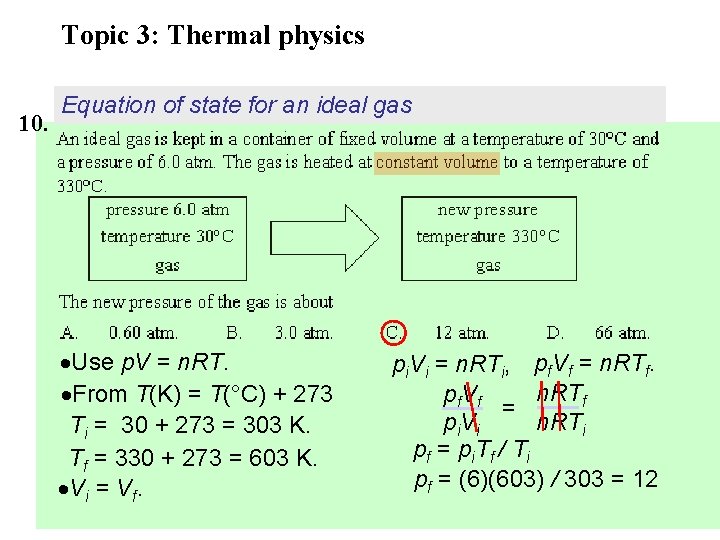
Topic 3: Thermal physics 10. Equation of state for an ideal gas Use p. V = n. RT. From T(K) = T(°C) + 273 Ti = 30 + 273 = 303 K. Tf = 330 + 273 = 603 K. Vi = Vf. pi. Vi = n. RTi, pf. Vf = n. RTf pf V f = n. RTi p i. V i p f = p i. T f / T i pf = (6)(603) / 303 = 12

Topic 3: Thermal physics 3. 2 – Modeling a gas Equation of state for an ideal gas For an ideal gas use p. V = n. RT. WANTED: n, the number of moles. GIVEN: p = 20 106 Pa, V = 2. 0 10 -2 m 3. From T(K) = T(°C) + 273 T(K) = 17 + 273 = 290 K. Then n = p. V / (RT) n = (20 106)(2 10 -2) / [ (8. 31)(290) ] n = 170 mol.

Topic 3: Thermal physics 11. Equation of state for an ideal gas Use n = N / NA where NA = 6. 02 1023 atoms / mol. Then N = n NA. 23 N = 170 mol 6. 02 10 atoms mol 26 N = 1. 0 10 atoms.

Ideal Gasses Recall the properties of an ideal gas: • • • Billions of tiny identical spherical molecules. Random motion. Each molecule zero volume. Elastic Collisions No intermolecular forces (PE) Individual forces on walls of container can be averaged over area to produce constant pressure.

Differences between real and ideal gases Real gases are often polyatomic (N 2, O 2, H 2 O, NH 4, etc. ) and thus not spherical. Ideal gases cannot be liquefied, but real gases have intermolecular forces and non-zero volume, so they can be liquefied. Real gases act like ideal gasses at low P and high volume. Intermolecular attractions minimized.

Topic 3: Thermal physics 3. 2 – Modeling a gas Differences between real and ideal gases

Volume vs. Temperature • What causes DT with changing volume? • Phet Gas Molecules

Motion of individual Molecules • Diffusion. • https: //www. youtube. com/watch? v=VY 0 m. ZUDvb. H 4&app=desktop • Brownian Motion. • Collisions between particles • https: //www. youtube. com/watch? v=4 m 5 Jn. JBq 2 AU

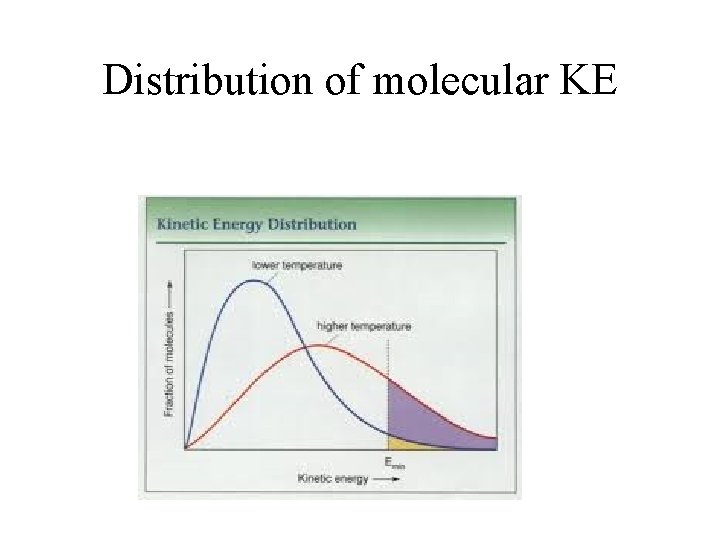
3. 2 – Modeling ideal gas KE Average kinetic/internal energy of an ideal gas Since ideal gases have no intermolecular forces, their internal energy is stored completely as KE. The individual molecules making up an ideal gas all travel at different speeds:

Distribution of molecular KE

Average EK of an ideal gas molecule is: EK of each ideal depends on mass and temperature. EK = (3/2) k. BT or 3 RT / 2 NA R = 8. 31 J / mol·K k. B is the Boltzmann constant.

EXAMPLE 1: 1) 2. 50 moles of hydrogen gas is contained in a fixed volume of 1. 25 m 3 at a temperature of 175 C. • a) What is the average kinetic energy of each atom? • b) What is the total internal energy of the gas?

SOLUTION: • T(K) = 175 + 273 = 448 K. • a) EK = (3/2) k. BT = (3/2)(1. 38 10 -23)(448) = 9. 27 10 -21 J. • b) From n = N / NA we get N = n. NA. • N = (2. 50 mol)(6. 02 1023 atoms / mol) = 1. 51 1024 atm. • EK = NEK = (1. 51 1024)(9. 27 10 -21 J) = 14000 J.

• EX 2: 2. 50 moles of hydrogen gas is contained in a fixed volume of 1. 25 m 3 at a temperature of 175 C. • c) What is the pressure of the gas at this temperature?

• SOLUTION: T(K) = 175 + 273 = 448 K. • c) Use p. V = n. RT: • p = n. RT / V • = 2. 50 8. 31 448 / 1. 25 • = 7450 Pa.

Particulate Nature of Matter and Changes of State 4 min. ok but not great. • https: //www. youtube. com/watch? v=ndw 9 X YA 4 i. F 0 Crash course ideal gasses 10 min https: //www. youtube. com/watch? v=Bx. US 1 K 7 xu 30

Hwk Packet

• Hwk DO Homer pg 113 #8 -11.

Eliminated from IB 2009

1. Why does blowing into a balloon increase its volume? • Blowing air into the balloon increases the # of air molecules, increasing the rate of collision inside the balloon, and increasing the pressure on the balloon wall.

Gas Laws Extra slides

Pressure Law At constant volume, Pa. T The ratio P is a constant T


What happens to the volume of a gas when the temperature decreases or increases?

What happens to the volume of a gas when the pressure is increased or decreased?

If temperature and pressure remain constant. . . What would happen to the volume of a gas if the number of moles (amount of molecules) is increased?

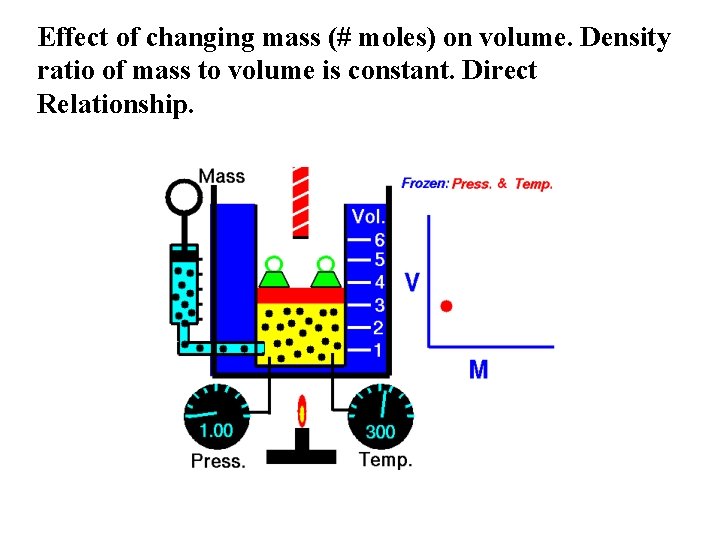
Effect of changing mass (# moles) on volume. Density ratio of mass to volume is constant. Direct Relationship.

What would happen to pressure of a gas as mass/moles increased?

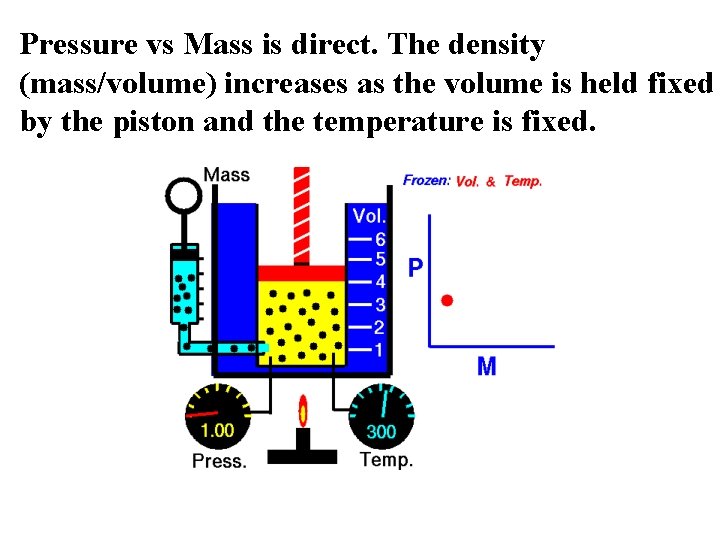
Pressure vs Mass is direct. The density (mass/volume) increases as the volume is held fixed by the piston and the temperature is fixed.

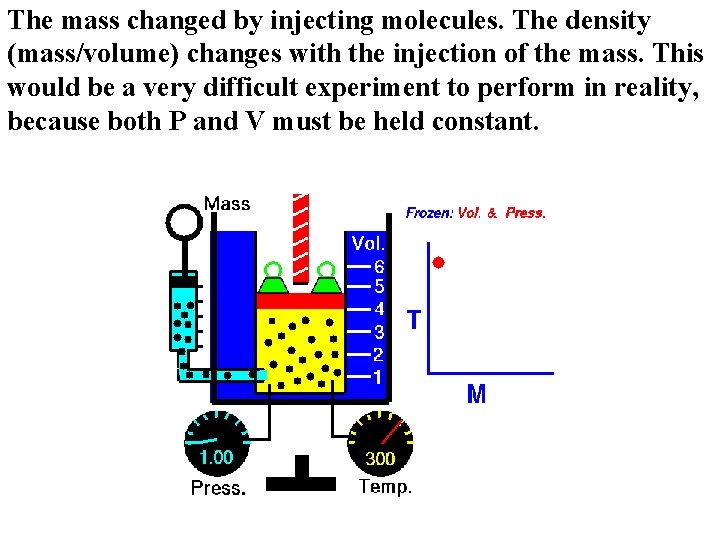
The mass changed by injecting molecules. The density (mass/volume) changes with the injection of the mass. This would be a very difficult experiment to perform in reality, because both P and V must be held constant.

To find # moles, n, in substance given the mass of substance. n = m M m = mass in g M = molar mass #g/mol from periodic table. 1 mole of any gas has fixed volume. At STP the volume is 22. 4 dm 3 or 22. 4 L.