Kinetic Energy AP Physics 1 thanks to Gabe

Kinetic Energy AP Physics 1 (thanks to Gabe Kessler, OCHS!)

End Slide Kinetic Energy KE = 1/2 mv 2 DKE = KEf – KEo = 1/2 mvf 2 – 1/2 mvo 2 Kinetic Energy is the energy stored in the motion of an object. A change in Kinetic Energy will also mean a change in speed (magnitude of velocity).

End Slide A man with a mass of 88 kg is running at 18. 0 m/s. What is his Kinetic Energy? KE = 1/2 mv 2 = 1/2(88)(18. 02) = 14300 J

End Slide A plane has a mass of 180, 000 kg and 1. 41 x 108 J of Kinetic Energy. What is the plane’s speed? KE = 1/2 mv 2 1. 41 x 108 = 1/2(180, 000)(v 2) 1. 41 x 108 = 90, 000 v 2 90, 000 v 2 = 15700 v = 125 m/s

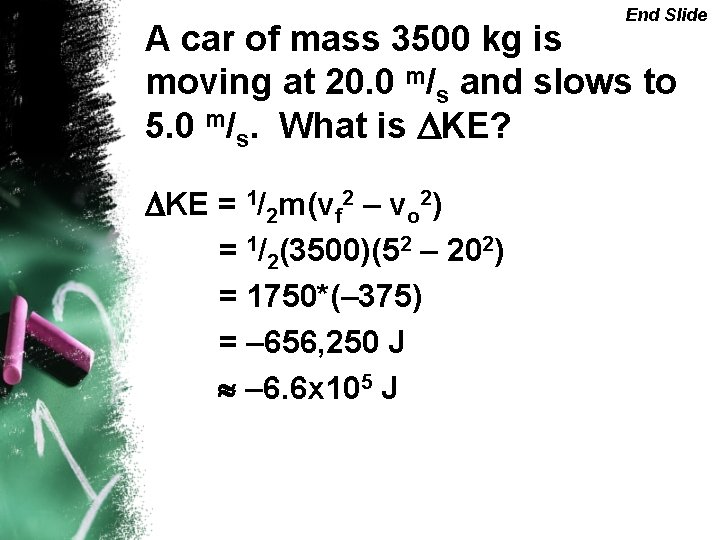
End Slide A car of mass 3500 kg is moving at 20. 0 m/s and slows to 5. 0 m/s. What is DKE? DKE = 1/2 m(vf 2 – vo 2) = 1/2(3500)(52 – 202) = 1750*(– 375) = – 656, 250 J » – 6. 6 x 105 J

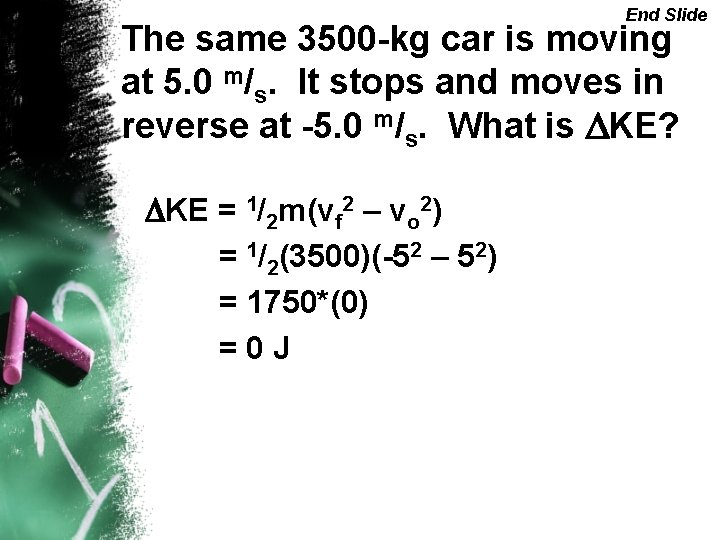
End Slide The same 3500 -kg car is moving at 5. 0 m/s. It stops and moves in reverse at -5. 0 m/s. What is DKE? DKE = 1/2 m(vf 2 – vo 2) = 1/2(3500)(-52 – 52) = 1750*(0) =0 J

End Slide Elastic Collision • For all collisions, momentum is conserved. • If Kinetic Energy is conserved (DKE = 0), then the collision is said to be elastic. • If Kinetic Energy is not conserved (DKE ¹ 0), then the collision is inelastic. • Realize that no collision is ever really perfectly elastic; however, some are close enough

End Slide Is this collision elastic? • Car 1 with a mass of 1200 kg moving at 25. 0 m/s strikes Car 2 with half of Car 1’s mass while it’s sitting still. Car 2 flies off at 30. 0 m/s while Car 1 moves at 10. 0 m/s. DKE 1 = 1/2 m 1(vf 12 – vo 12) = 1/2(1200)(102 – 252) = -315, 000 J DKE 2 = 1/2 m 2(vf 22 – vo 22) = 1/2(600)(302 – 02) = 270, 000 J DKE 1+DKE 2 = -315, 000+270, 000 = -45, 000 J

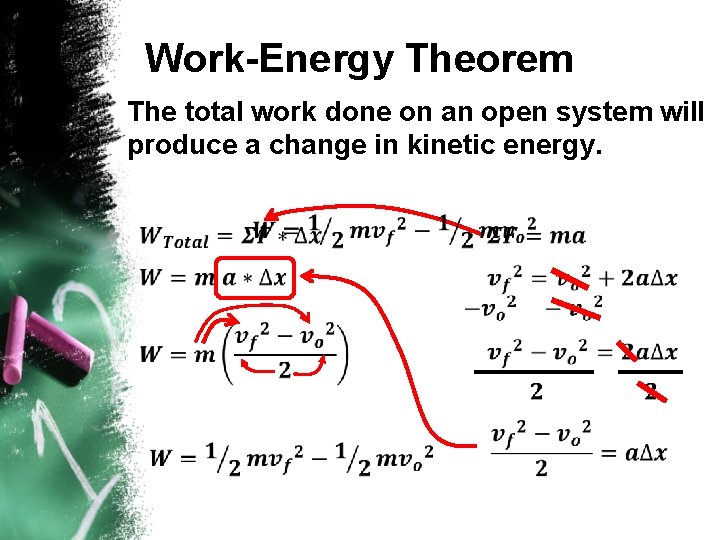
Work-Energy Theorem The total work done on an open system will produce a change in kinetic energy.

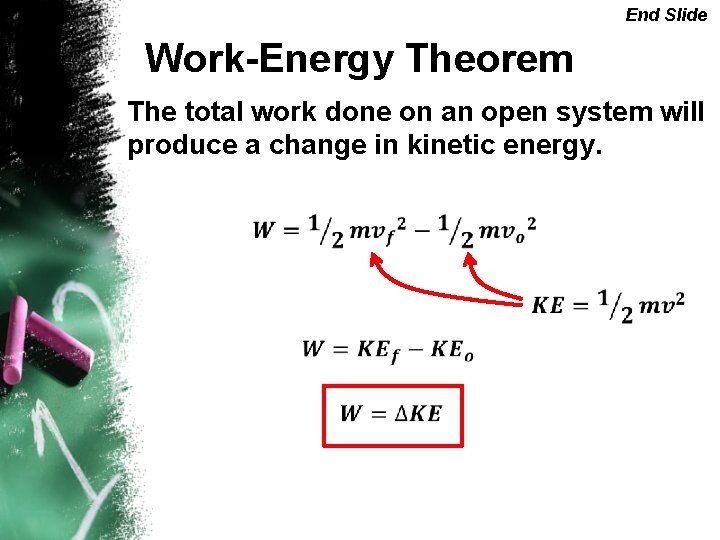
End Slide Work-Energy Theorem The total work done on an open system will produce a change in kinetic energy.

End Slide A horizontal force of 3250 N is applied to a 110 -kg mass initially at rest for a horizontal distance of 0. 15 m. What is the final velocity of the mass? W = DKE F*Dx = 1/2 m(vf 2 – vo 2) (3250)(0. 15) = 1/2(110) (vf 2 – 02) 487. 5 J = 55 vf 2 = 8. 86 m 2/s 2 vf = 2. 98 m/s

End Slide A 105 -g hockey puck is sliding across the ice at 1. 3 m/s. A player exerts a constant 4. 50 -N force to give the puck a velocity of 3. 8 m/s. For what distance did the player apply the force to the puck? W = DKE Þ F*Dx = 1/2 m(vf 2 – vo 2) 4. 50 Dx = 1/2(0. 105)(3. 82 – 1. 32) 4. 50 Dx = 0. 0525*(12. 75) 4. 50 Dx = 0. 6694 J Dx = 0. 149 m

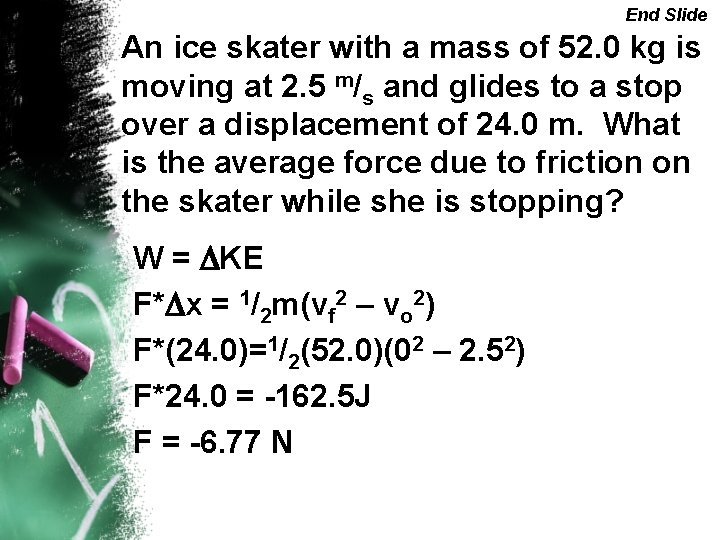
End Slide An ice skater with a mass of 52. 0 kg is moving at 2. 5 m/s and glides to a stop over a displacement of 24. 0 m. What is the average force due to friction on the skater while she is stopping? W = DKE F*Dx = 1/2 m(vf 2 – vo 2) F*(24. 0)=1/2(52. 0)(02 – 2. 52) F*24. 0 = -162. 5 J F = -6. 77 N