Kinematyka Panta rhei Heraklit 500 lat p n





![Przypadek jednowymiarowy: przyspieszenie chwilowe miarą nachylenia stycznej do wykresu prędkości od czasu V [m/s] Przypadek jednowymiarowy: przyspieszenie chwilowe miarą nachylenia stycznej do wykresu prędkości od czasu V [m/s]](https://slidetodoc.com/presentation_image_h2/45557c946e89678bb417e3bd2e57096e/image-20.jpg)
![Ruch jednostajnie przyspieszony [m/s] v. K v 0 t [s] Ruch jednostajnie przyspieszony [m/s] v. K v 0 t [s]](https://slidetodoc.com/presentation_image_h2/45557c946e89678bb417e3bd2e57096e/image-21.jpg)


- Slides: 24

Kinematyka Panta rhei (Heraklit 500 lat p. n. e. )

Ruch najpowszechniejszą obserwacją - przemieszczanie się - transformacja (panta rei) Kinematyka – opis i klasyfikacja ruchów (przemieszczeń)

Ruch jest względny

(delta) – czyli zmiana • Gdyby „zamrozić czas” nie byłoby żadnej zmiany!!! • Dlatego ∆ to zawsze zmiana, która zaszła w jakimś czasie • Jeśli ten czas jest bardzo, bardzo krótki – to deltę grecką zastępujemy literką d

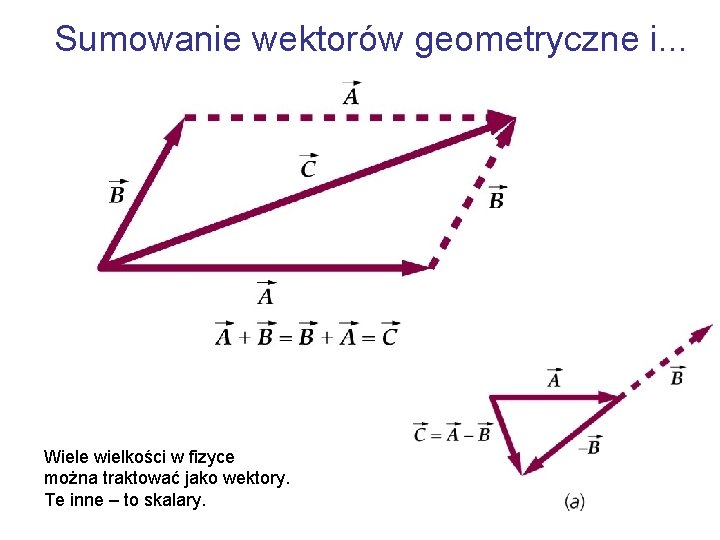
Sumowanie wektorów geometryczne i. . . Wiele wielkości w fizyce można traktować jako wektory. Te inne – to skalary.

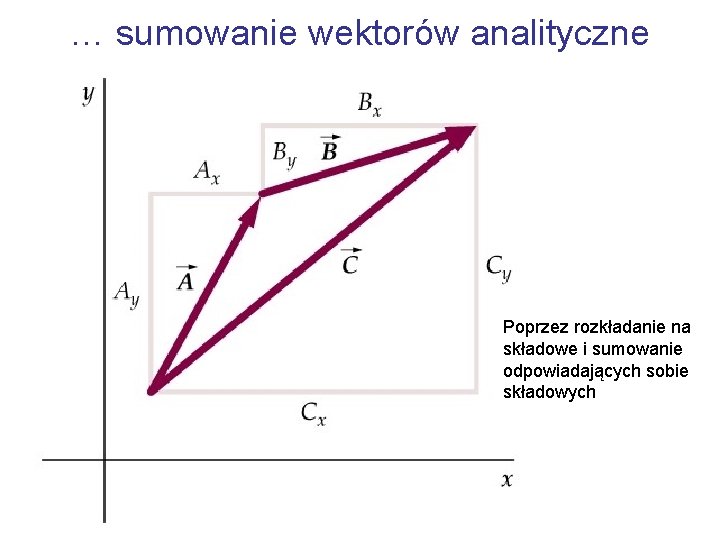
… sumowanie wektorów analityczne Poprzez rozkładanie na składowe i sumowanie odpowiadających sobie składowych

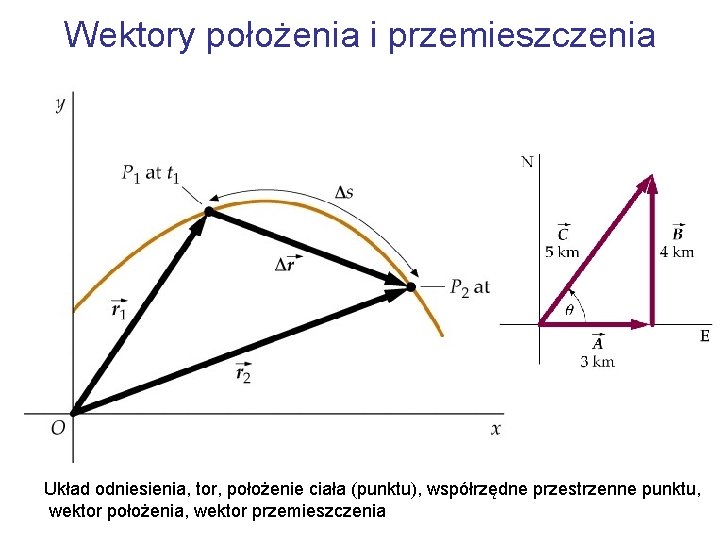
Wektory położenia i przemieszczenia Układ odniesienia, tor, położenie ciała (punktu), współrzędne przestrzenne punktu, wektor położenia, wektor przemieszczenia

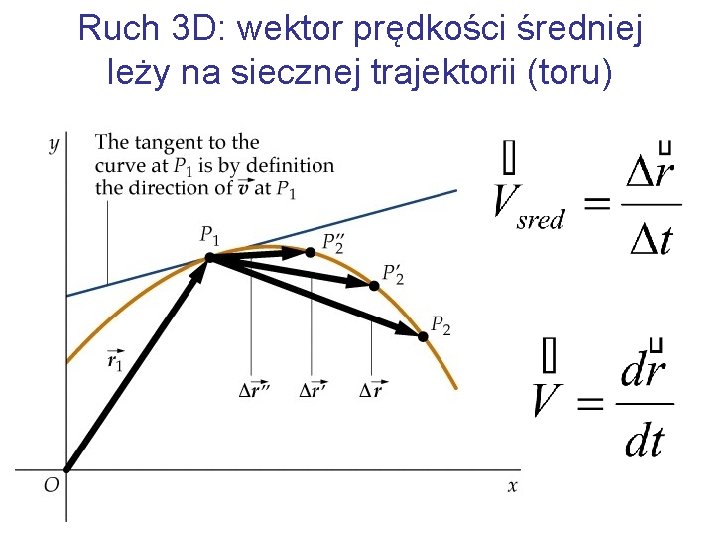
Ruch 3 D: wektor prędkości średniej leży na siecznej trajektorii (toru)

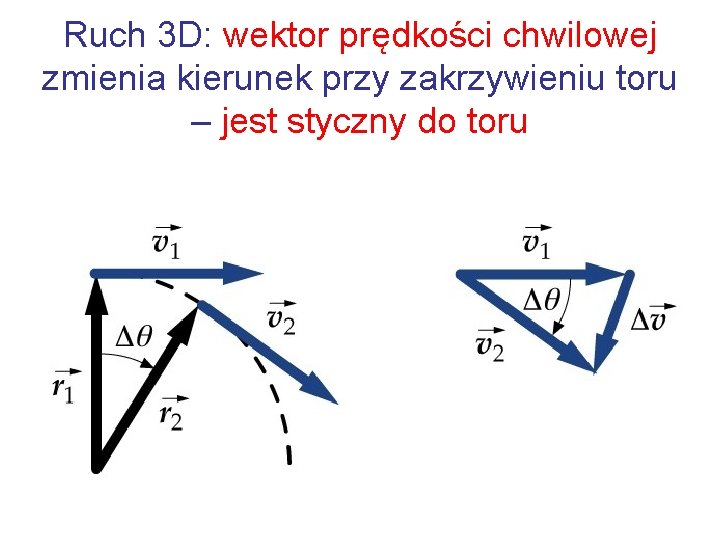
Ruch 3 D: wektor prędkości chwilowej zmienia kierunek przy zakrzywieniu toru – jest styczny do toru

Przypadek jednowymiarowy ≠ ruch po prostej Przypadek jednowymiarowy = ruch, w którym interesuje nas jedynie przebyta odległość • Nie ma potrzeby zajmować się wtedy wektorem prędkości • Mówiąc prędkość mamy wtedy na myśli wartość wektora prędkości czyli szybkość • Velocity – prędkość wektorowa, a czasem wartość prędkości • Speed – szybkość, tylko skalar

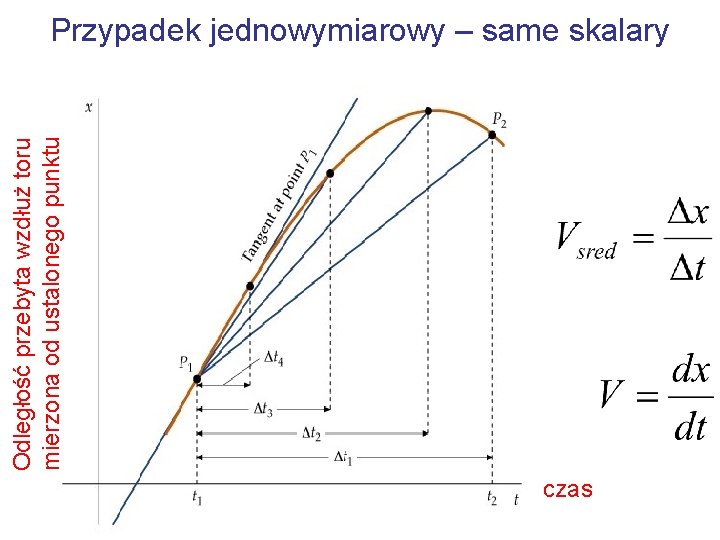
Odległość przebyta wzdłuż toru mierzona od ustalonego punktu Przypadek jednowymiarowy – same skalary czas

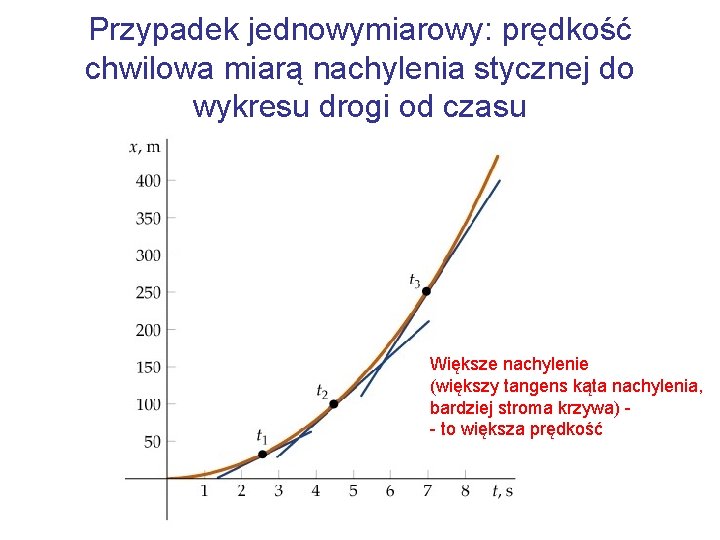
Przypadek jednowymiarowy: prędkość chwilowa miarą nachylenia stycznej do wykresu drogi od czasu Większe nachylenie (większy tangens kąta nachylenia, bardziej stroma krzywa) - to większa prędkość

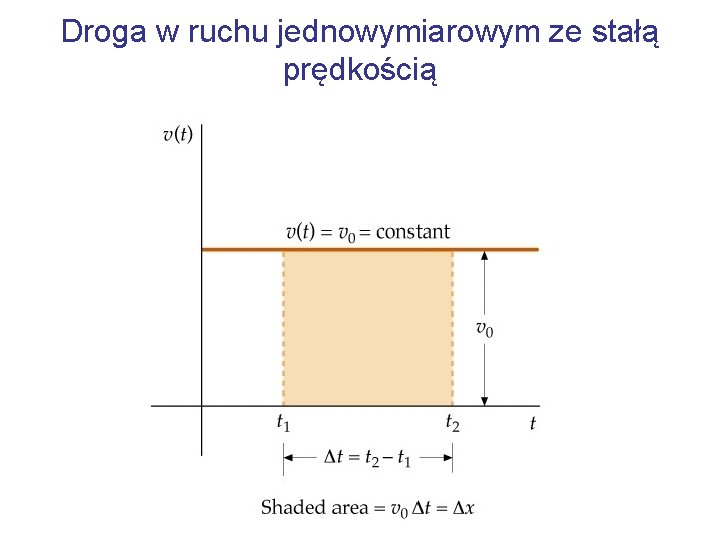
Droga w ruchu jednowymiarowym ze stałą prędkością

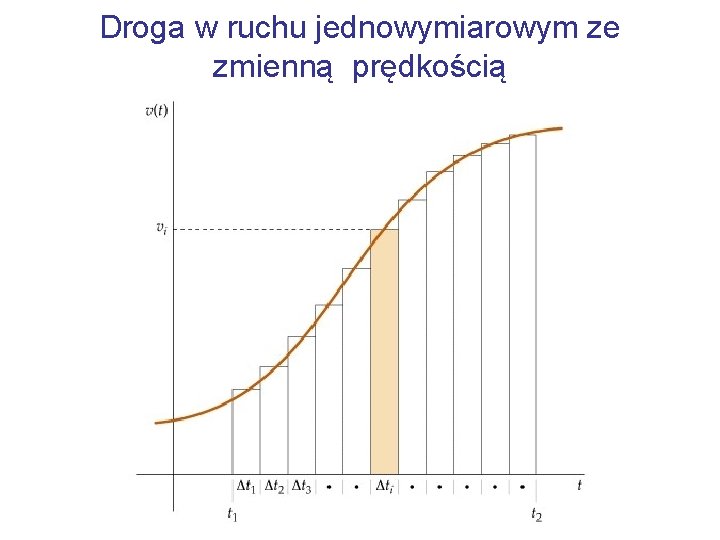
Droga w ruchu jednowymiarowym ze zmienną prędkością

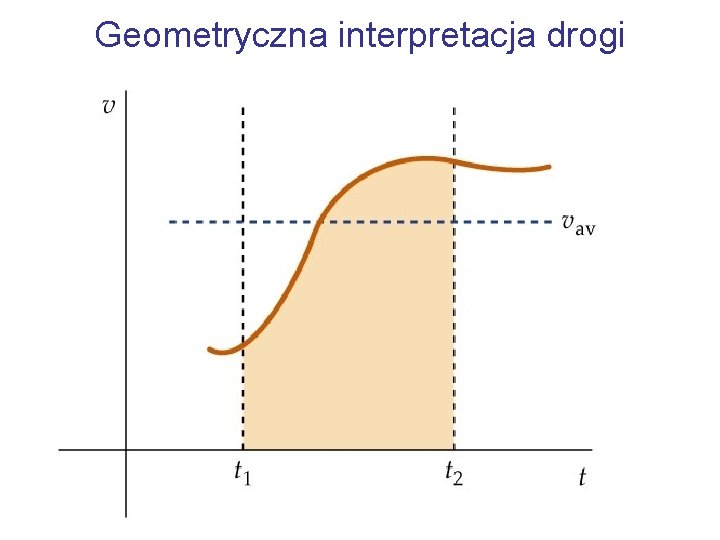
Geometryczna interpretacja drogi

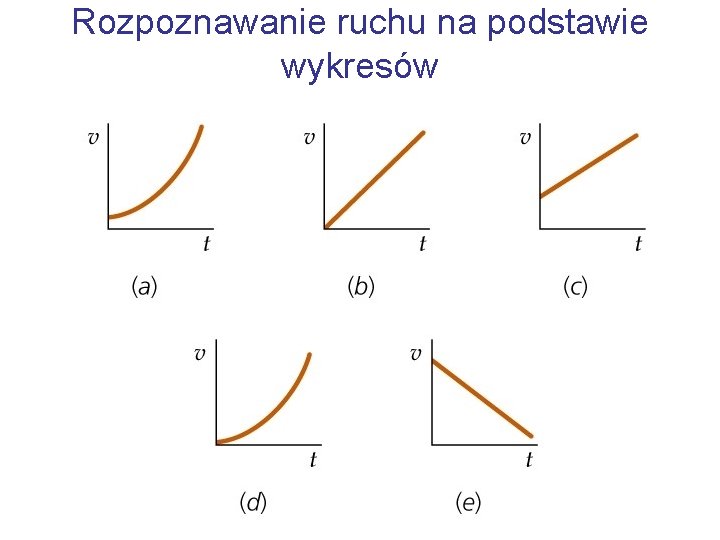
Rozpoznawanie ruchu na podstawie wykresów

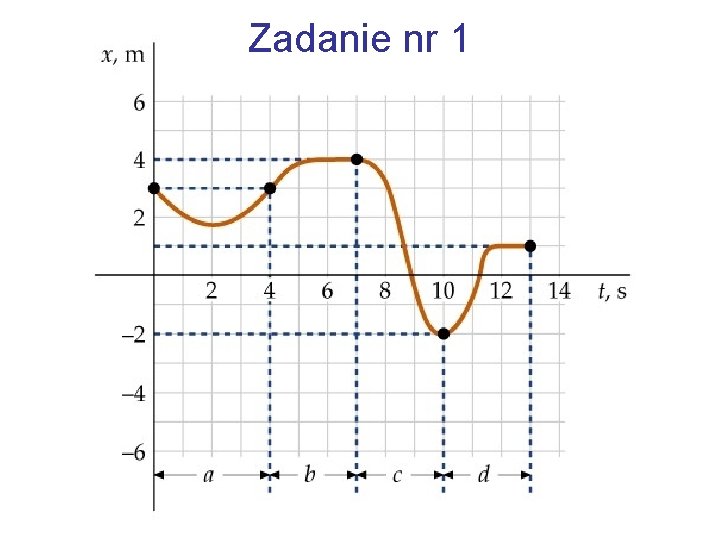
Zadanie nr 1

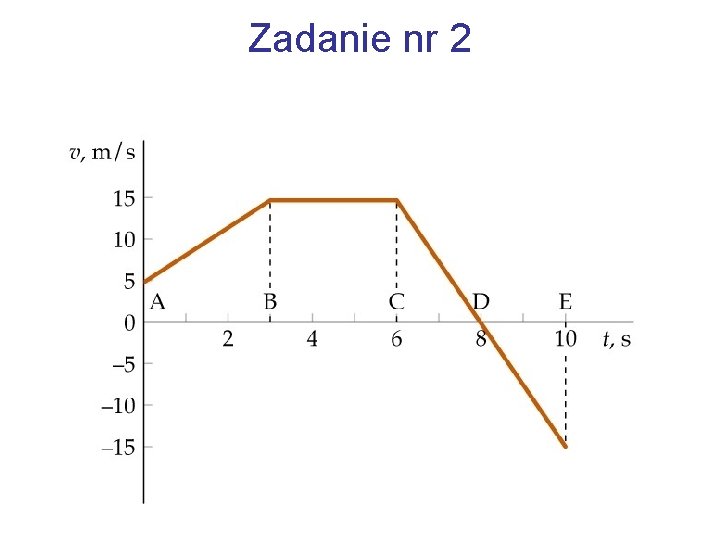
Zadanie nr 2

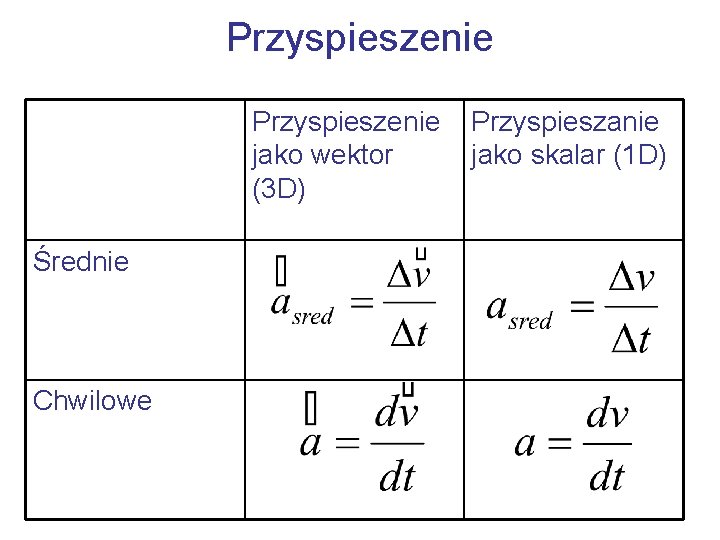
Przyspieszenie jako wektor (3 D) Średnie Chwilowe Przyspieszanie jako skalar (1 D)
![Przypadek jednowymiarowy przyspieszenie chwilowe miarą nachylenia stycznej do wykresu prędkości od czasu V ms Przypadek jednowymiarowy: przyspieszenie chwilowe miarą nachylenia stycznej do wykresu prędkości od czasu V [m/s]](https://slidetodoc.com/presentation_image_h2/45557c946e89678bb417e3bd2e57096e/image-20.jpg)
Przypadek jednowymiarowy: przyspieszenie chwilowe miarą nachylenia stycznej do wykresu prędkości od czasu V [m/s] Większe nachylenie (większy tangens kąta nachylenia, bardziej stroma krzywa) - to większe przyspieszenie
![Ruch jednostajnie przyspieszony ms v K v 0 t s Ruch jednostajnie przyspieszony [m/s] v. K v 0 t [s]](https://slidetodoc.com/presentation_image_h2/45557c946e89678bb417e3bd2e57096e/image-21.jpg)
Ruch jednostajnie przyspieszony [m/s] v. K v 0 t [s]

Najważniejszy wzór dla ruchu jednostajnie przyspieszonego Droga: s (albo x)

Jedna z jego konsekwencji… • Drogi przebyte w kolejnych sekundach (jeśli v 0 było równe zeru) mają się do siebie jak kolejne liczby nieparzyste

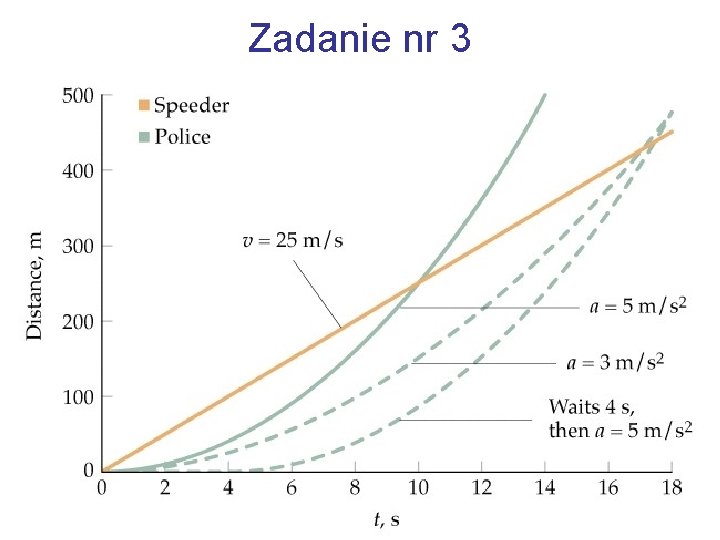
Zadanie nr 3