Kinematics n The 3 Kinematic equations There are

Kinematics n

The 3 Kinematic equations There are 3 major kinematic equations than can be used to describe the motion in DETAIL. All are used when the acceleration is CONSTANT.

Kinematics for the VERTICAL Direction All 3 kinematics can be used to analyze one dimensional motion in either the X direction OR the y direction.

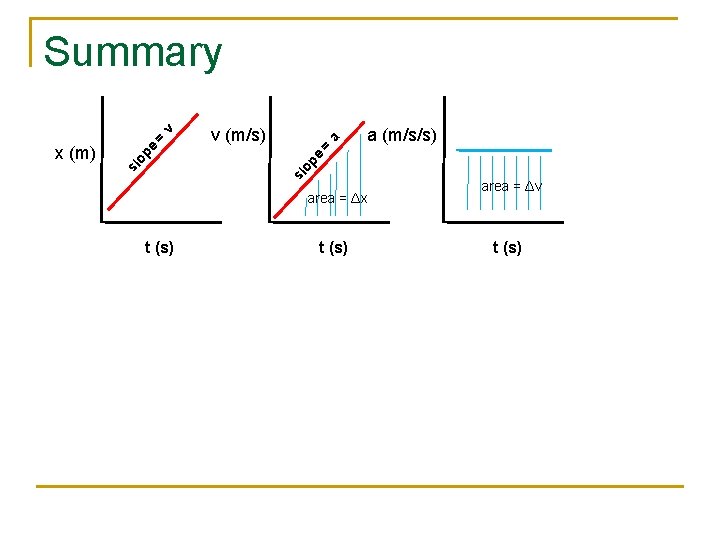
a (m/s/s) = a v (m/s) sl op e e op sl x (m) = v Summary area = Δx t (s) area = Δv t (s)

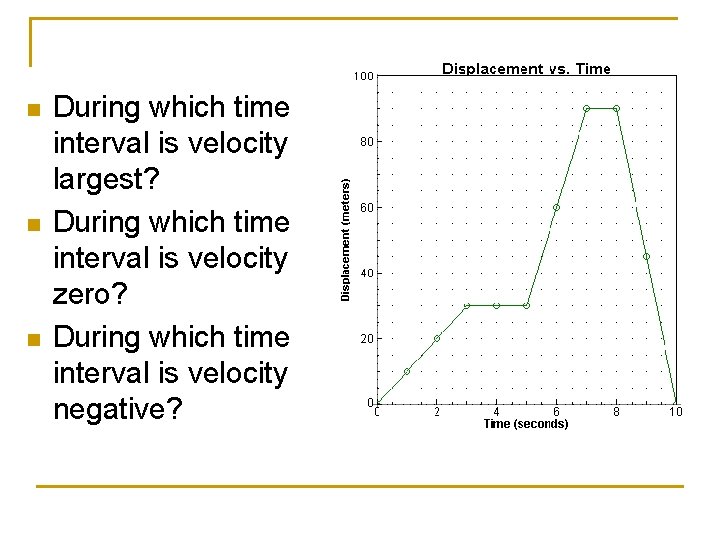
n n n During which time interval is velocity largest? During which time interval is velocity zero? During which time interval is velocity negative?

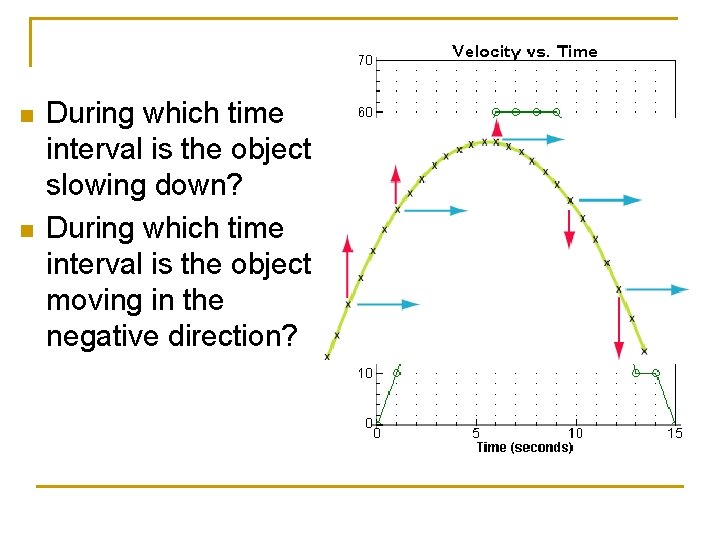
n n During which time interval is the object slowing down? During which time interval is the object moving in the negative direction?

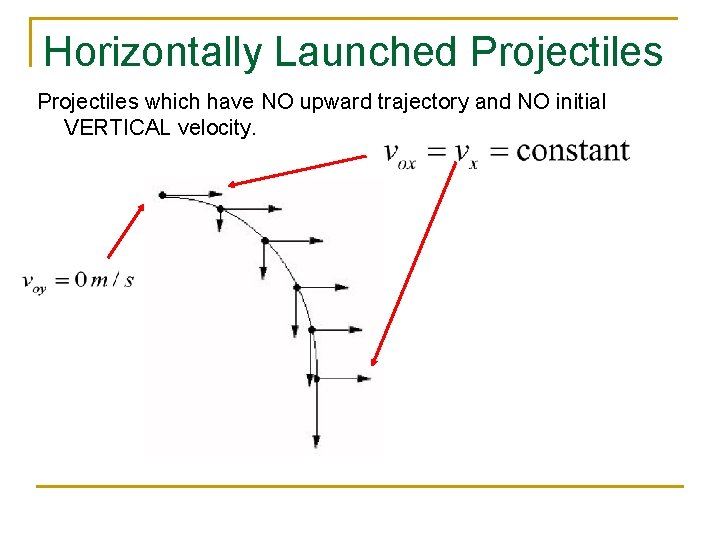
Horizontally Launched Projectiles which have NO upward trajectory and NO initial VERTICAL velocity.

Horizontally Launched Projectiles To analyze a projectile in 2 dimensions we need 2 equations. One for the “x” direction and one for the “y” direction. And for this we use kinematic #2. Remember, the velocity is CONSTANT horizontally, so that means the acceleration is ZERO! Remember that since the projectile is launched horizontally, the INITIAL VERTICAL VELOCITY is equal to ZERO.

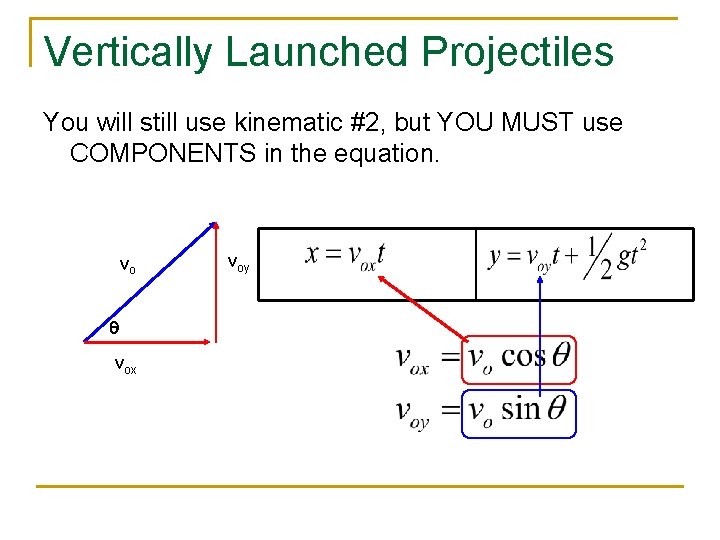
Vertically Launched Projectiles You will still use kinematic #2, but YOU MUST use COMPONENTS in the equation. vo q vox voy

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (a) How long is the ball in the air? (b) How far away does it land? (c) How high does it travel? /s m 0 0. v 2 = o q = 53

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (a) How long is the ball in the air? 3. 26 s What I know What I want to know vox=12. 04 m/s t = ? voy=15. 97 m/s x = ? y = 0 ymax=? g = - 9. 8 m/s/s

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (b) How far away does it land? What I know What I want to know vox=12. 04 m/s t = 3. 26 s voy=15. 97 m/s x = ? y = 0 ymax=? g = - 9. 8 m/s/s 39. 24 m

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (c) How high does it travel? What I know What I want to know vox=12. 04 m/s t = 3. 26 s voy=15. 97 m/s x = 39. 24 m y = 0 ymax=? g = - 9. 8 m/s/s CUT YOUR TIME IN HALF! 13. 01 m

Newton’s First Law – The Law of Inertia INERTIA – a quantity of matter, also called MASS. Italian for “LAZY”. Unit for MASS = kilogram. Weight or Force due to Gravity is how your MASS is effected by gravity. NOTE: MASS and WEIGHT are NOT the same thing. MASS never changes When an object moves to a different planet. What is the weight of an 85. 3 -kg person on earth? On Mars=3. 2 m/s/s)?

Newton’s First Law An object in motion remains in motion in a straight line and at a constant speed OR an object at rest remains at rest, UNLESS acted upon by an EXTERNAL (unbalanced) Force.

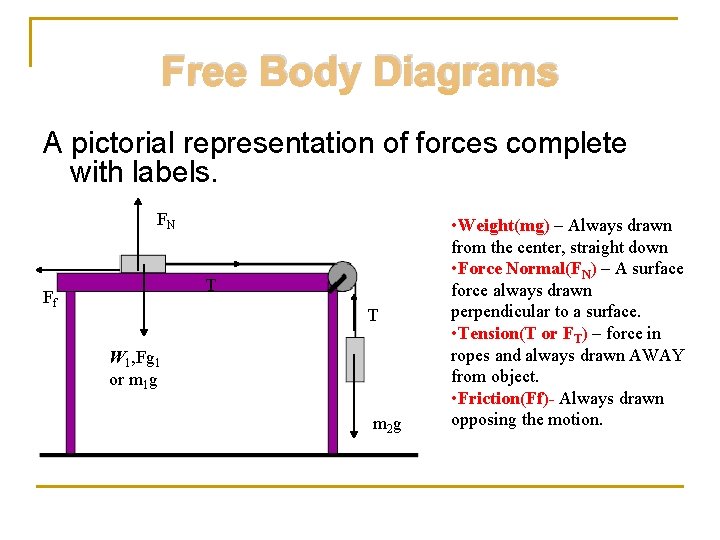
Free Body Diagrams A pictorial representation of forces complete with labels. FN T Ff T W 1, Fg 1 or m 1 g m 2 g • Weight(mg) – Always drawn from the center, straight down • Force Normal(FN) – A surface force always drawn perpendicular to a surface. • Tension(T or FT) – force in ropes and always drawn AWAY from object. • Friction(Ff)- Always drawn opposing the motion.

Newton’s Second Law The acceleration of an object is directly proportional to the NET FORCE and inversely proportional to the mass. Tips: • Draw an FBD • Resolve vectors into components • Write equations of motion by adding and subtracting vectors to find the NET FORCE. Always write larger force – smaller force. • Solve for any unknowns

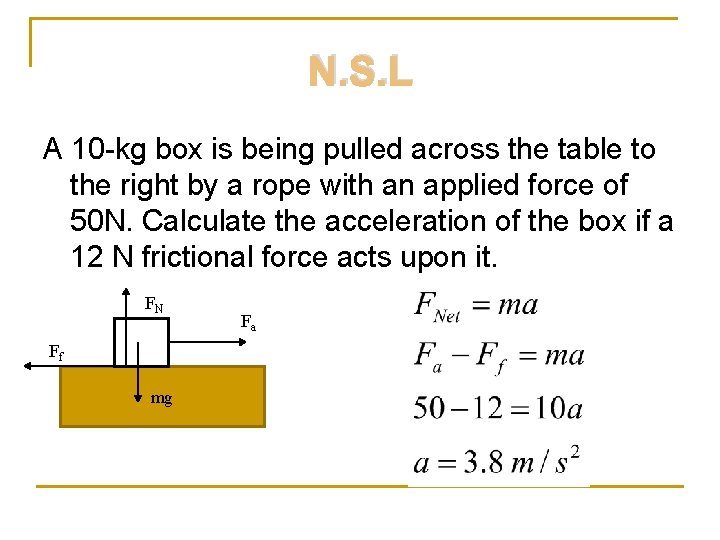
N. S. L A 10 -kg box is being pulled across the table to the right by a rope with an applied force of 50 N. Calculate the acceleration of the box if a 12 N frictional force acts upon it. FN Ff mg Fa

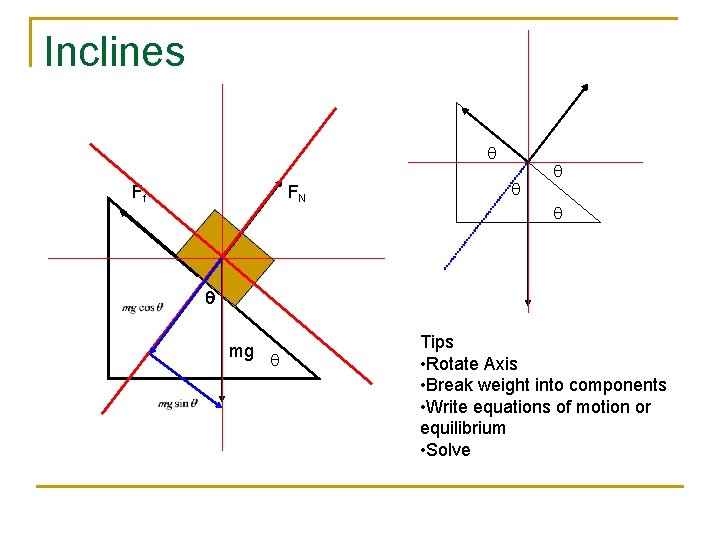
Inclines q Ff FN q q mg q Tips • Rotate Axis • Break weight into components • Write equations of motion or equilibrium • Solve

Newton’s Third Law “For every action there is an EQUAL and OPPOSITE reaction. n n This law focuses on action/reaction pairs (forces) They NEVER cancel out All you do is SWITCH the wording! • PERSON on WALL • WALL on PERSON

Work Done by a Force Work can be found by W = F*d*cosϴ Work is also equal to the change in energy n Measured in joules n n

Power n n