Kinematics Motion in a straight line The diagram

Definition Distance from a given position with an associated sign is called Displacement. Units

Acceleration 3 m/s 13 m/s A B In the diagram above let’s say that

30 m/s A 6 m/s B In the diagram above let’s say that a

Here we can write down the formula for acceleration as Acceleration = Here we

With u = the initial velocity v = the final velocity t = time

Example A car accelerates from a velocity of 16 m/s to a velocity of

Example Initially, a particle P is moving with uniform acceleration 6 m/s 2 has

Example A body moves along a straight line from A to B with Uniform

Example The displacement from its original position of a particle moving with uniform acceleration

Example A car decelerates from a velocity of 36 m/s. The magnitude of the

Example A stone slides in a straight line across a horizontal sheet of ice.

Slides: 12

Download presentation

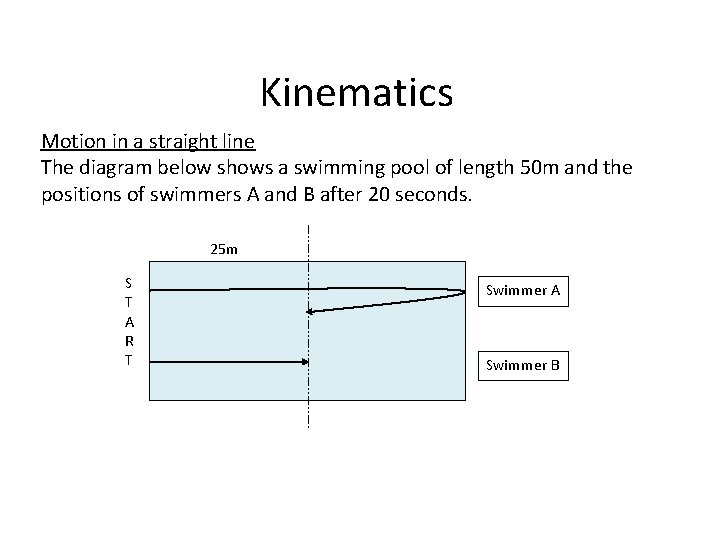
Kinematics Motion in a straight line The diagram below shows a swimming pool of length 50 m and the positions of swimmers A and B after 20 seconds. 25 m S T A R T Swimmer A Swimmer B

Definition Distance from a given position with an associated sign is called Displacement. Units are always m. Definition The Velocity of a body has a magnitude (size) and an associated sign. Units are always m/s or written ms-1 The above workings make use of the following triangle of formulae for Distance, speed, time. D S T

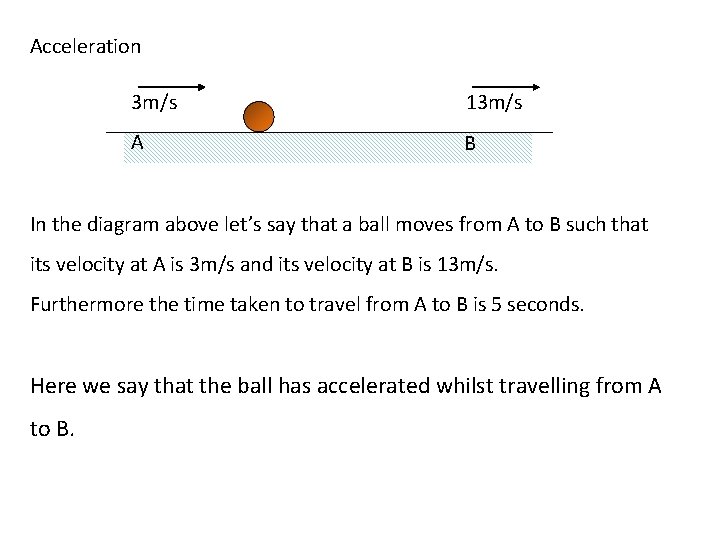
Acceleration 3 m/s 13 m/s A B In the diagram above let’s say that a ball moves from A to B such that its velocity at A is 3 m/s and its velocity at B is 13 m/s. Furthermore the time taken to travel from A to B is 5 seconds. Here we say that the ball has accelerated whilst travelling from A to B.

30 m/s A 6 m/s B In the diagram above let’s say that a ball moves from A to B such that its velocity at A is 30 m/s and its velocity at B is 6 m/s. Furthermore the time taken to travel from A to B is 6 seconds. Here we say that the ball has decelerated whilst travelling from A to B.

Here we can write down the formula for acceleration as Acceleration = Here we have the basics of the formulae required in kinematics a um/s vm/s A t=0 B t s

With u = the initial velocity v = the final velocity t = time taken s = displacement a = acceleration (constant) Then we may use the following formulae to solve any number of problems!

Example A car accelerates from a velocity of 16 m/s to a velocity of 40 m/s in a distance of 500 m. Calculate the acceleration of the car.

Example Initially, a particle P is moving with uniform acceleration 6 m/s 2 has a velocity at the point O of 3 m/s. Find its velocity after 2 s and its displacement from O after 4 s.

Example A body moves along a straight line from A to B with Uniform acceleration �m/s 2. The time taken is 12 seconds and the velocity at B is 25 m/s. Find (i) The velocity at A (ii) The distance AB.

Example The displacement from its original position of a particle moving with uniform acceleration is 6 m after 2 s and 20 m after 4 s. Find the displacement 6 s after the start of the motion.

Example A car decelerates from a velocity of 36 m/s. The magnitude of the deceleration is 3 m/s 2. Calculate the time required to cover a distance of 162 m.

Example A stone slides in a straight line across a horizontal sheet of ice. It passes point A with velocity 14 m/s, and point B 2�seconds later where AB = 30. Retardation is uniform. Calculate a) The velocity at B b) The retardation c) The time and displacement from A at which the stone comes to rest.