Kinematics Graphical Analysis of Motion Kinematics Frame of

Kinematics: Graphical Analysis of Motion

Kinematics Frame of Reference The object or background used to determine motion and its direction. The frame of reference is assumed/defined to be at rest. Everything around us has motion (you, the wall, the air, etc). There is no matter that we know of that doesn’t have some type of motion associated with it.

Kinematics All objects move relative to some frame of reference. I’m moving relative to a moving car. The earth is moving relative to the sun. Two cars passing each other are moving relative to the ground and each other.

Kinematics The study of motion requires three basic measurements: 1. a. Distance (d): How far it is from one position to another. Measured in units of length – meters (m), feet (ft), miles (mi), etc. b. Displacement (d): the straight line distance between an object’s initial and final positions. i. Units are the same as distance.

Kinematics 2. Direction: How the position changes relative to the starting point. north, east; (+), (–); up, down, left, right; 30 o, 160 o; etc. 3. Time (t): Event duration (start to finish). Irreversible and is measured in seconds (s), minutes (min), hours (hr), etc.

Kinematics Scalars vs Vectors Scalars represent only magnitude. ($20, 35 kg, 150 mph, etc. ) Vectors represent magnitude and direction (150 mph north, 30 m southeast, etc. ) Vectors are represented by arrows. The arrow’s length represents magnitude. Where the arrow is pointed represents direction.

Kinematics How Fast (Speed vs Velocity)? Speed (Scalar Quantity) (v) – Rate at which a distance is covered. Calculated by dividing the distance by the time interval (v = d / t). The units are: any distance over any time. 1. Instantaneous Speed – the speed measured at a specific point (instant – speedometer). 2. Average Speed – the total distance covered divided the total time of the event; what most people mean when they say “speed”.

Kinematics Velocity (Vector Quantity) (v) – the speed and direction of the motion. 1. Velocity = change in position (displacement (Δ x)). Δ = “change in” or “final – initial” and x = position. For an object to have velocity, the initial and final positions must be different. Velocity is found by dividing displacement by the time interval (v = d / t). 2. Instantaneous Velocity is measured at a specific point (instant – speedometer).

Kinematics Acceleration (vector quantity) (a): the rate of change in velocity during a time interval (how quickly speed changes) 1. Acceleration is found by dividing the change in velocity by the time interval (a = Δ v / t). The units are velocity over time or distance over time squared (a = d / t 2). An object must do one of these three to accelerate: speed up, slow down, or change direction.

Kinematics An increase in speed is acceleration. A decrease in speed is deceleration (a negative acceleration). In scientific language, both of these are considered accelerations. Distance and speed are scalar quantities. Displacement, velocity and acceleration are vector quantities.

Kinematics is the study of how an object moves. It is not concerned with why an object moves or what causes the object’s motion. Kinematics consists of two parts. 1. The Graphical Analysis of Motion 2. The Solving of Kinematics Problems

Kinematics – Part One (Graphical Analysis of Motion) Motion can be described using four quantities – time, displacement, velocity, and acceleration. Pictures of these quantities are called graphs. The relationships between these quantities will be studied by looking at these graphs.

Kinematics – Part One (Graphical Analysis of Motion) The relationships between these quantities will then be studied through formulas. 1. These formulas will be used to solve problems (Part Two – Solving of Kinematics Problems)

Graphical Analysis of Motion There are three different types of graphs in the study of different types of motion. 1. The position time graph (position on the y axis, time on the x axis) 2. The velocity time graph (velocity on the y axis, time on the x axis) 3. The acceleration time graph (acceleration on the y axis, time on the x axis) These three graphs are analyzed together for each kind of motion to be studied.

Graphical Analysis of Motion Facts about these graphs you must know (very important). 1. slope of position time graph = velocity 2. slope of velocity time graph = acceleration 3. area under velocity time graph = displacement 4. area under acceleration time graph = change in velocity 5. only constant acceleration (horizontal straight lines on the AT graph) in this course

Graphical Analysis of Motion These types of motion will be analyzed as to how they occur in relation to a motion detector as demonstrated in lab. 1. No motion, standing still 2. Motion toward the motion detector 3. Motion away from the motion detector

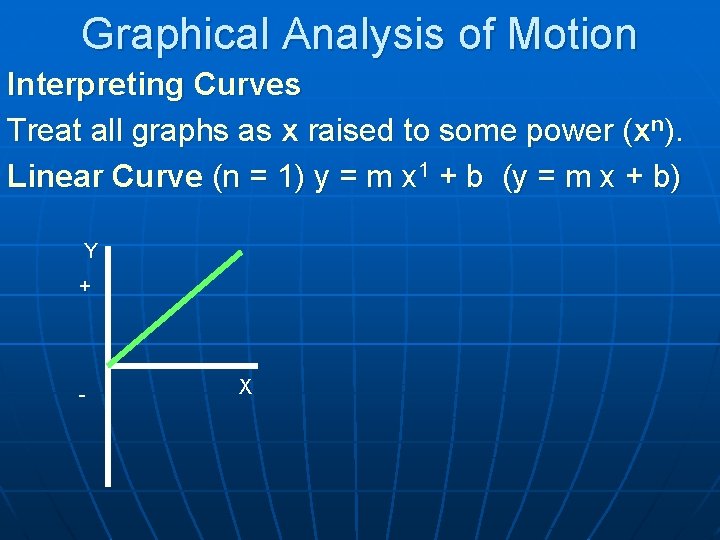
Graphical Analysis of Motion Interpreting Curves Treat all graphs as x raised to some power (xn). Linear Curve (n = 1) y = m x 1 + b (y = m x + b) Y + - X

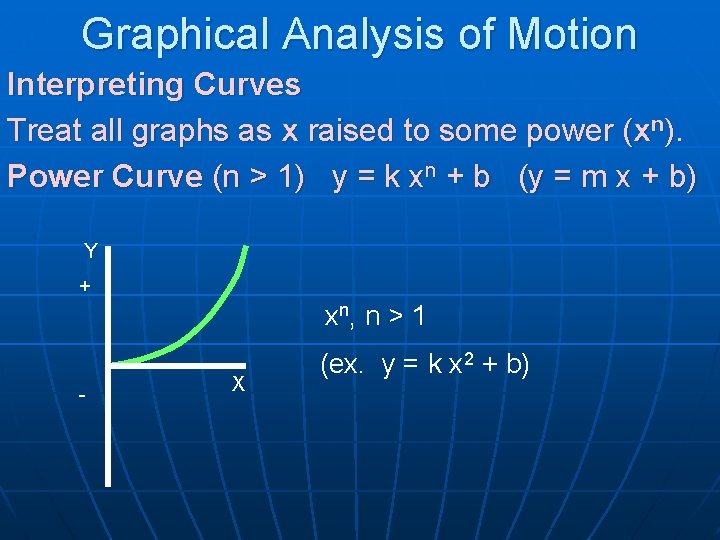
Graphical Analysis of Motion Interpreting Curves Treat all graphs as x raised to some power (xn). Power Curve (n > 1) y = k xn + b (y = m x + b) Y + xn, n > 1 - X (ex. y = k x 2 + b)

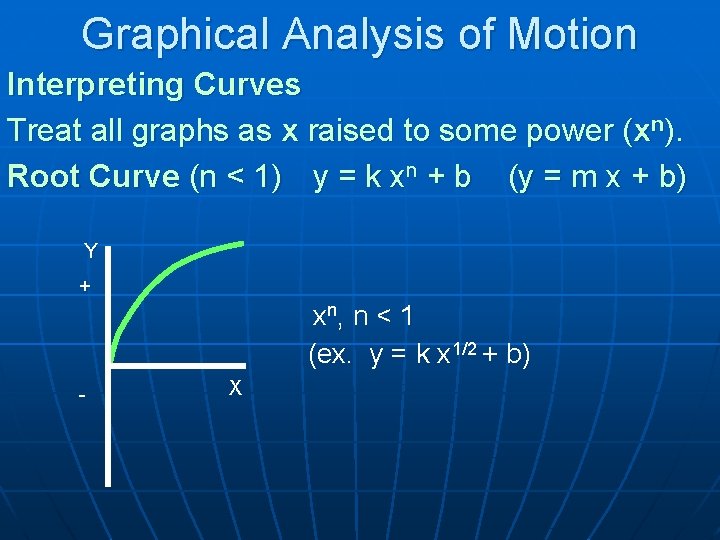
Graphical Analysis of Motion Interpreting Curves Treat all graphs as x raised to some power (xn). Root Curve (n < 1) y = k xn + b (y = m x + b) Y + xn, n < 1 (ex. y = k x 1/2 + b) - X

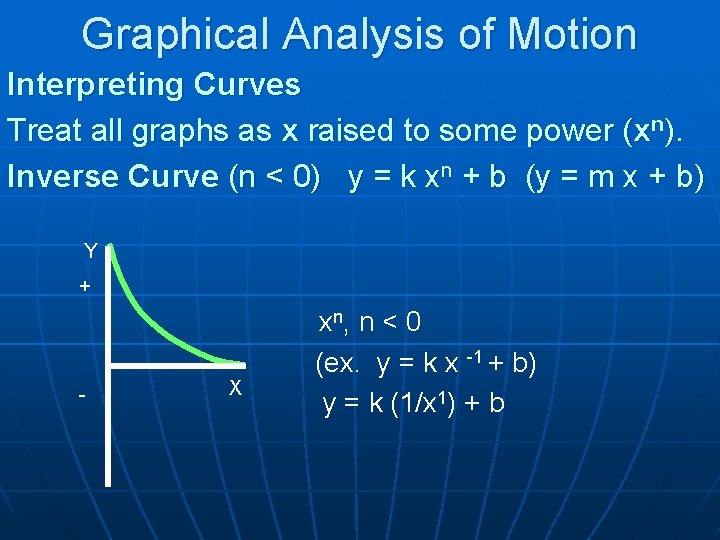
Graphical Analysis of Motion Interpreting Curves Treat all graphs as x raised to some power (xn). Inverse Curve (n < 0) y = k xn + b (y = m x + b) Y + - X xn, n < 0 (ex. y = k x -1 + b) y = k (1/x 1) + b

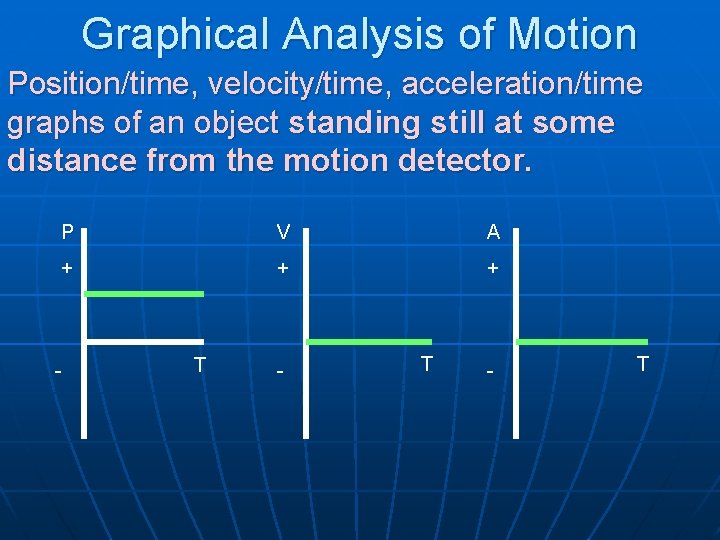
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object standing still at some distance from the motion detector. P V A + + + - T - T

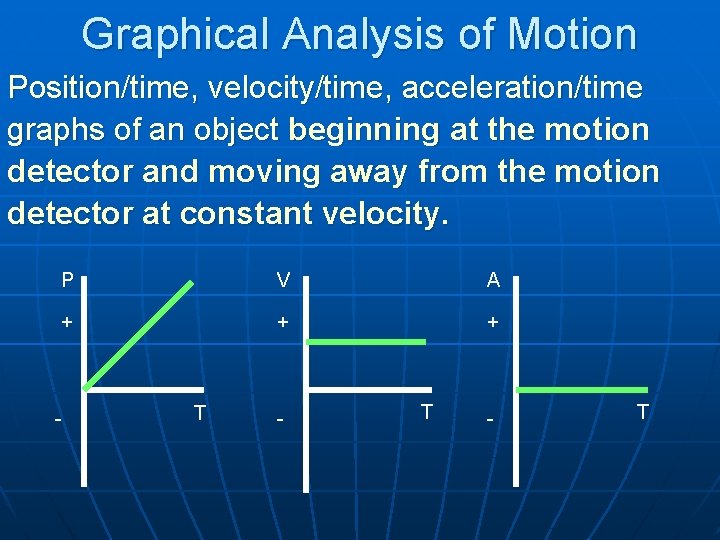
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object beginning at the motion detector and moving away from the motion detector at constant velocity. P V A + + + - T - T

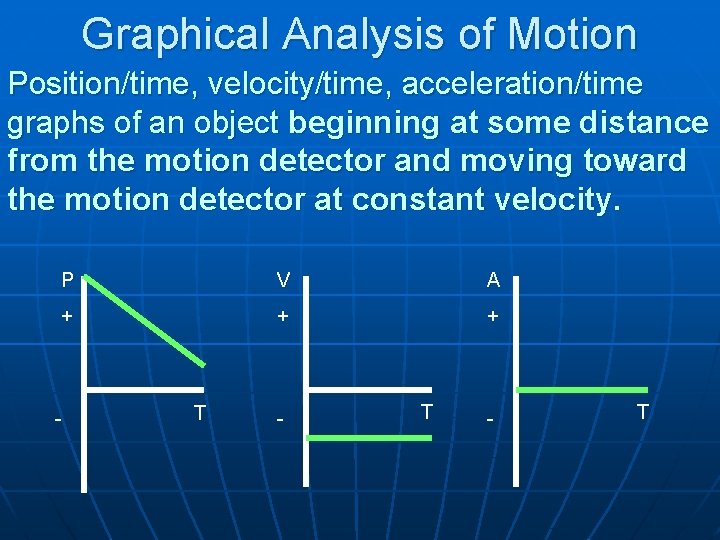
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object beginning at some distance from the motion detector and moving toward the motion detector at constant velocity. P V A + + + - T - T

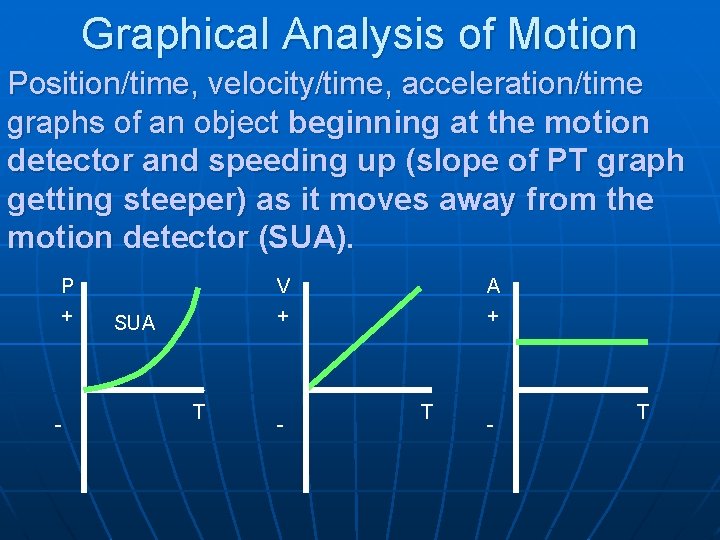
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object beginning at the motion detector and speeding up (slope of PT graph getting steeper) as it moves away from the motion detector (SUA). P + - V + SUA T - A + T - T

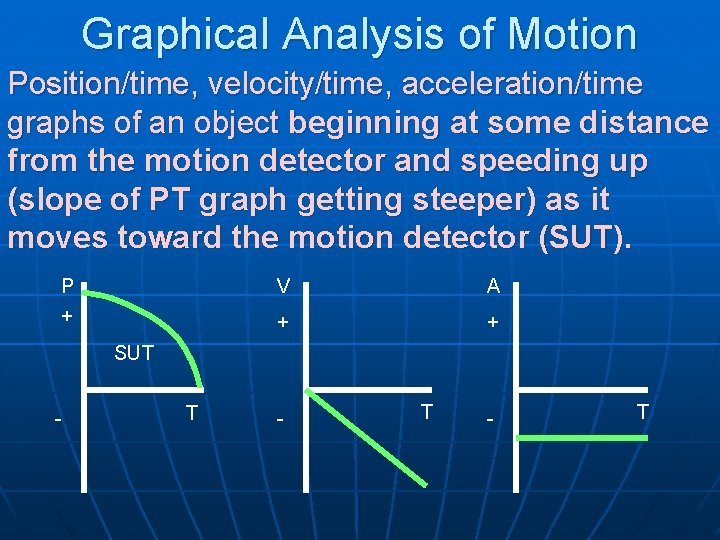
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object beginning at some distance from the motion detector and speeding up (slope of PT graph getting steeper) as it moves toward the motion detector (SUT). P + V A + + SUT - T - T

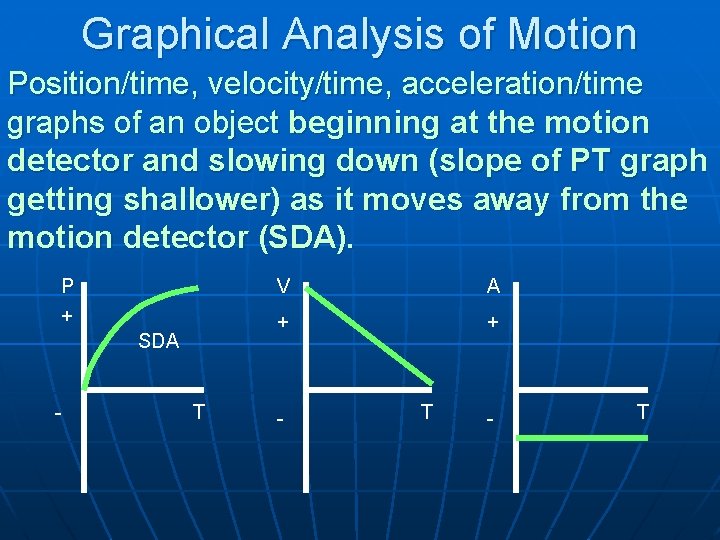
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object beginning at the motion detector and slowing down (slope of PT graph getting shallower) as it moves away from the motion detector (SDA). P + SDA - T V A + + - T

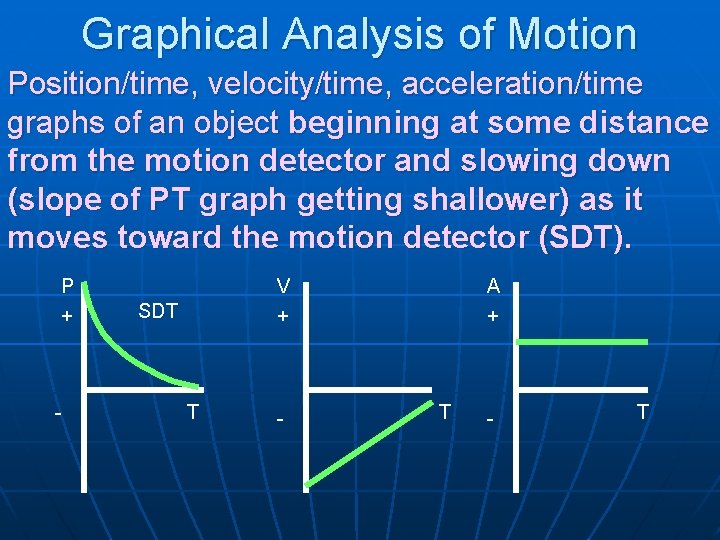
Graphical Analysis of Motion Position/time, velocity/time, acceleration/time graphs of an object beginning at some distance from the motion detector and slowing down (slope of PT graph getting shallower) as it moves toward the motion detector (SDT). P + - V + SDT T - A + T - T

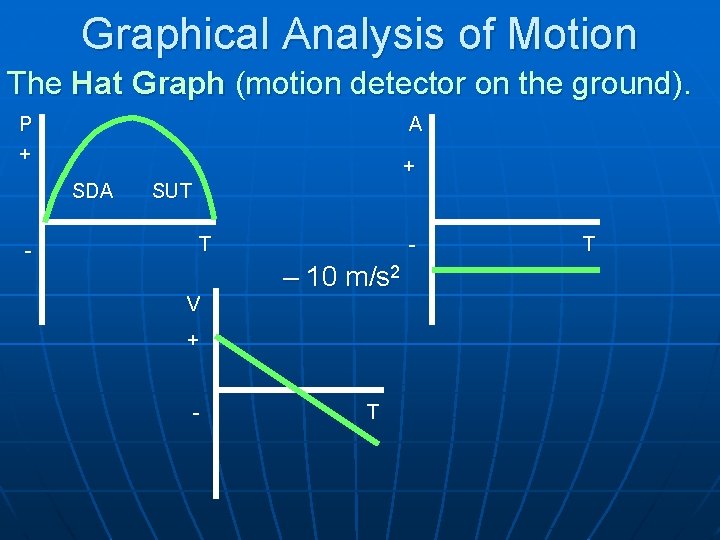
Graphical Analysis of Motion 1. An object is thrown straight up into the air and the motion detector is on the ground. The only force acting on it is gravity if you neglect air resistance. A. There will be two parts to this graph because the object is first moving straight up then moving straight down. B. The affectionate name of the PT graph of this motion is the hat graph.

Graphical Analysis of Motion The Hat Graph (motion detector on the ground). P + A + SDA - SUT T V - – 10 m/s 2 + - T T

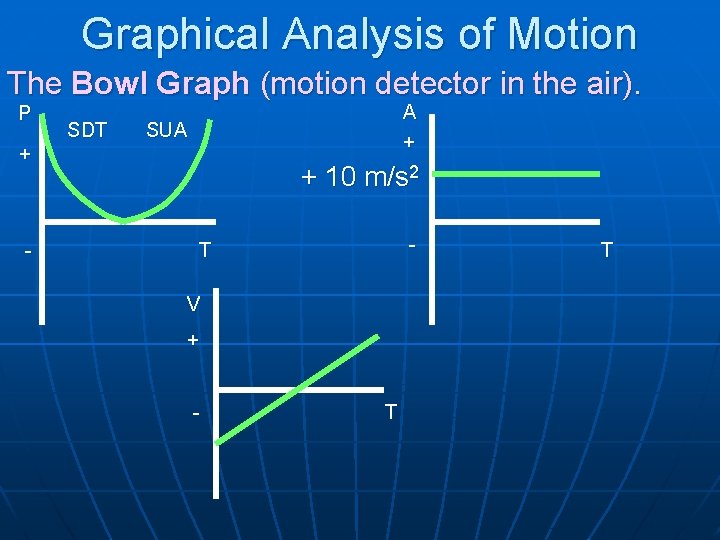
Graphical Analysis of Motion 2. An object is thrown straight up into the air and the motion detector is up in the air. The only force acting on it is gravity if you neglect air resistance. A. There will be two parts to this graph because the object is first moving straight up then moving straight down. B. The affectionate name of the PT graph of this motion is the bowl graph.

Graphical Analysis of Motion The Bowl Graph (motion detector in the air). P SDT A + SUA + - + 10 m/s 2 - T V + - T T

Kinematics – Part Two Solving Kinematics Problems The following constant acceleration equations are derived from the motion graphs. All the derived equations can be simplified if the problem deals with motion that starts from rest (vi = 0). 1. vf = vi + a t becomes: vf = a t 2. d = vi t + ½ a t 2 becomes: d = ½ a t 2 3. vf 2 = vi 2 + 2 a d becomes: vf 2 = 2 a d Another important equation is as follows: 4. d = ½ (vf + vi)

Kinematics – Part Two Solving Kinematics Problems All objects, no matter what their mass, density, or shape fall to the earth from a given release point with the same free-fall acceleration, g. Free fall means falling in a vacuum, so that the frictional resistance and buoyant effect of the air do not affect the objects motion. This quantity, g, is called the acceleration due to gravity.

Kinematics – Part Two Solving Kinematics Problems The direction of g at any point determines the direction of the vertical at that point – what is meant by “down. ” The magnitude of g varies from point to point on the earth’s surface. Its average value is about – 10 m/s 2 (about 32 ft/s 2). This value will be used for the problems in this unit.

Kinematics – Part Two Solving Kinematics Problems For problems with freely falling objects, a coordinate system is implemented. If the object is moving upward ___. 1. d (distance/displacement) is positive (+) 2. v (velocity) is positive (+) 3. a (acceleration) is negative (–) – 10 m (on the earth at sea level) s 2

Kinematics – Part Two Solving Kinematics Problems If the object is moving downward ___. 1. d (distance/displacement) is negative (–) 2. v (velocity) is negative (–) 3. a (acceleration) is negative (–) – 10 m (on the earth at sea level) s 2 (speeding up in the (– ( ) direction)

Graphing Motion With Numbers Remember these rules. 1. Slope of position time graph = velocity. 2. Slope of velocity time graph = acceleration. 3. Area under velocity time graph = displacement.

Kinematics: Two Dimensional Motion

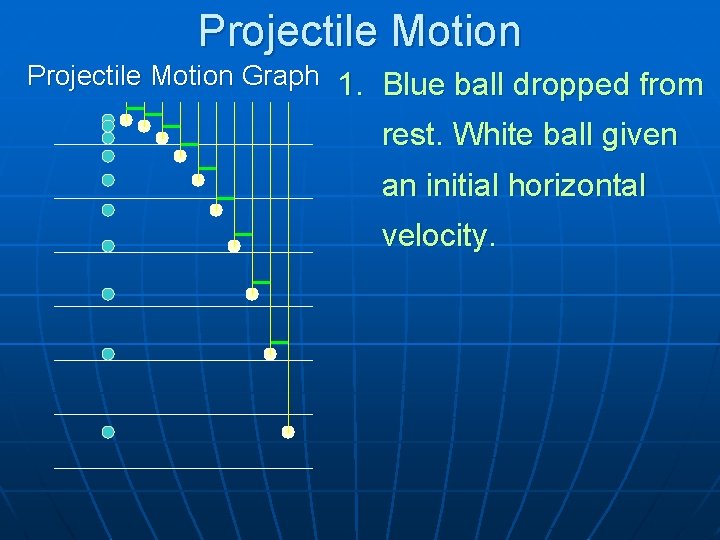
Projectile Motion 1. Objects thrown into the air and influenced by gravity only (neglecting air friction) are called projectiles (i. e. footballs, arrows, baseballs, bullets, etc). 2. Projectile (curved) motion is considered free fall motion with an initial horizontal velocity. 3. During their flight, projectiles follow true parabolic paths (if there is no air resistance).

Projectile Motion Graph 1. Blue ball dropped from rest. White ball given an initial horizontal velocity.

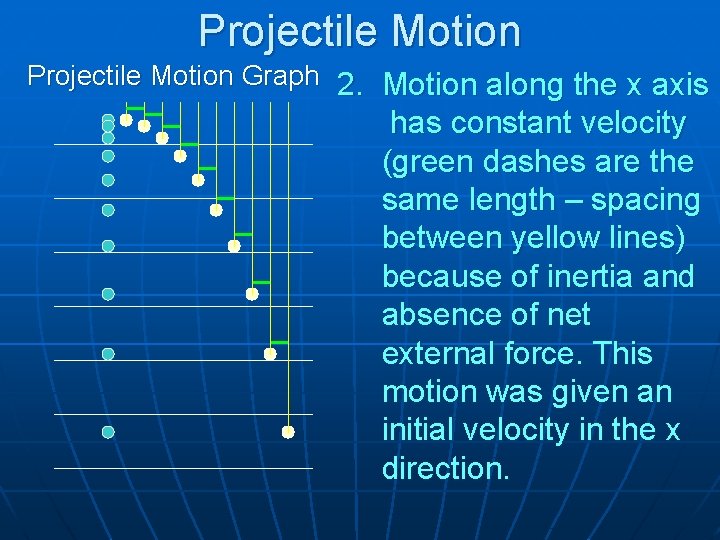
Projectile Motion Graph 2. Motion along the x axis has constant velocity (green dashes are the same length – spacing between yellow lines) because of inertia and absence of net external force. This motion was given an initial velocity in the x direction.

Projectile Motion Graph 3. The motion (for both balls) along the y axis have a constant acceleration (due to the constant force of Earth pulling on the object and giving it weight. This motion (for both balls) was begun at rest in the y direction.

Projectile Motion 4. The constant acceleration (y direction motion) and the constant velocity (x direction motion) of the white ball give its trajectory a parabolic shape.

Projectile Motion 5. As shown in the previous projectile motion graph, notice that the blue and the white balls are still falling at the same rate even though the white ball was given an initial horizontal velocity. The horizontal white lines are evenly spaced time constants (i. e. 1 sec, 2 sec, etc. ).

Projectile Motion 6. The x axis motion and the y axis motion are both acting simultaneous to each other and are independent of each other.

Projectile Motion 7. As shown in the previous projectile motion graph, a projectile launched horizontally and one dropped from the same height at the same time will hit the ground at the same time but not at the same place. 8. Equation for the horizontal motion of a projectile: dx = v x t

Projectile Motion 9. Equations for vertical motion of a projectile that falls from rest: (a = g, viy = 0) A. vyf = a t B. vyf 2 = 2 a dy C. dy = ½ a t 2

Projectile Motion If you want to find the velocity at any time in flight of either ball, find the vector sum of the x and y components of the velocity at that point. Then use the Pythagorean Theorem to find the magnitude of the velocity and the tangent function to find the direction of the velocity. The blue ball will have no x component.

Projectile Motion 1. Projectiles can also be launched at an angle (θ) above the horizontal. These kinds of problems fall into two categories. A. The point where they land can be level with the point where they were launched. B. The point where they land can be either higher or lower than the point where they were launched.

Projectile Motion The landing site of the projectile shown in the following slides, launched at an angle (θ) above the horizontal (blue lines) is level with its launch site. Remember that the path of a projectile launched at an angle above the horizontal is not a graph of position versus time.

Projectile Motion 1. The horizontal velocity is the same throughout the flight, as indicated by the green arrows. 2. Vertical velocity decreases as object goes up and increases as object goes down (yellow arrows). The resultant of the horizontal and vertical components of velocity are tangent to the curve of flight (resultant vector on # 8). 2 1 θ 3 4 5 6 7 8 9

Projectile Motion 3. When the projectile is at the same height, whether it’s going up or down, its vertical velocity is the same in magnitude but opposite in direction. This is indicated by the lengths of the yellow arrows. A. vy of 1, same mag. - opposite dir. as vy of 9. B. vy of 2, same mag. - opposite dir. as vy of 8. C. vy of 3, same mag. - opposite dir. as vy of 7. D. vy of 4, same mag. - opposite dir. as vy of 6. (mag. = magnitude, dir. = direction)

Projectile Motion 4. Notice with position number 5, there is no y component of velocity (vy) (no yellow arrow). A. For this reason, the top of the flight path (apex) is the point where the total velocity (vertical and horizontal components added together) is the least for a projectile launched at an angle above the horizontal.

Projectile Motion 5. Since the final landing site is level with the initial launch site, the final vertical velocity (vyf) is equal in magnitude and opposite in direction to the initial vertical velocity (vyi) (yellow arrows).

Projectile Motion Initial velocity (vi) of a projectile launched at an angle is split up into horizontal (vix) and vertical (viy) components. vi viy θ 1. vix = vi (cos θ) 2. viy = vi (sin θ) vix Substitute equations 1 and 2 into kinematics equations to obtain equations that can be used to analyze the motion of a projectile launched at an angle.

Projectile Motion The kinematics equations mentioned in the previous slide are as follows: 1. vix = vi (cos θ) = constant 2. dx = vi (cos θ) t 3. vyf = vi (sin θ) + a t 4. vyf 2 = vi 2 (sin θ)2 + 2 a dy 5. dy = vi (sin θ) t + ½ a t 2 (x direction, a = 0) (y direction, a ≠ 0)