KINEMATICS ANALYSIS OF ROBOTS Part 5 Kinematics Analysis

KINEMATICS ANALYSIS OF ROBOTS (Part 5)

Kinematics Analysis of Robots V This lecture continues the discussion on the analysis of the forward and inverse kinematics of robots. After this lecture, the student should be able to: • Solve problems of robot forward and inverse kinematics analysis using transformation matrices
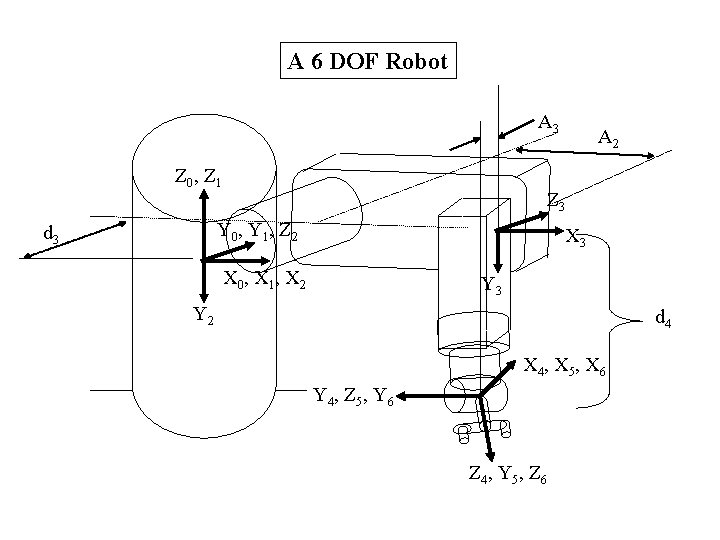
A 6 DOF Robot A 3 Z 0 , Z 1 Z 3 Y 0 , Y 1 , Z 2 d 3 A 2 X 3 X 0 , X 1 , X 2 Y 3 Y 2 d 4 X 4 , X 5 , X 6 Y 4 , Z 5 , Y 6 Z 4 , Y 5 , Z 6
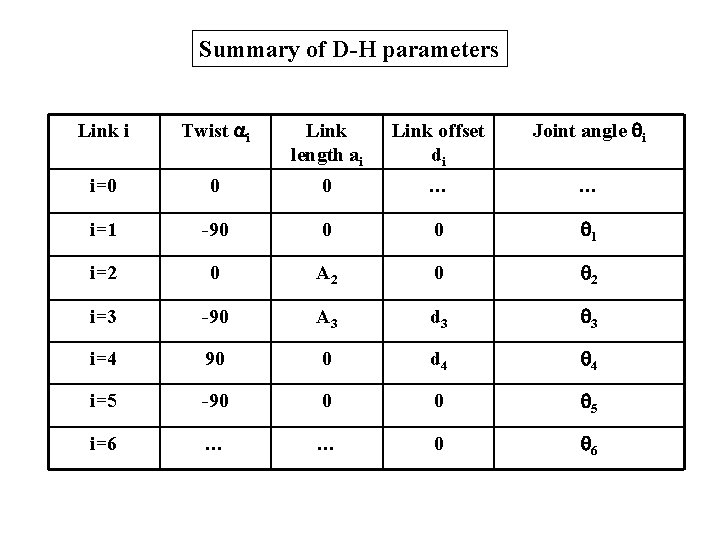
Summary of D-H parameters Link i Twist i Link length ai Link offset di Joint angle i i=0 0 0 … … i=1 -90 0 0 1 i=2 0 A 2 0 2 i=3 -90 A 3 d 3 3 i=4 90 0 d 4 4 i=5 -90 0 0 5 i=6 … … 0 6

Transformation matrices

Transformation matrices

Transformation matrices
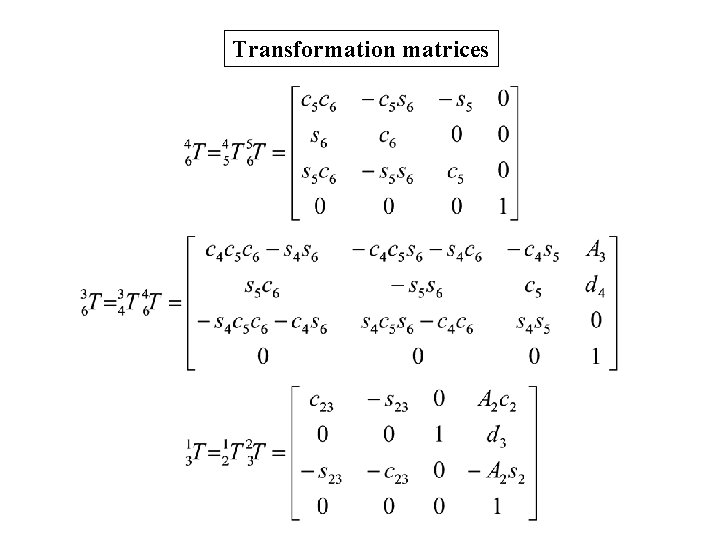
Transformation matrices

Transformation matrices

Transformation matrices

Transformation matrices

Forward Kinematics Given all the joint angles ( 1, 2, 3, 4, 5, and 6) we can use the overall transformation matrix to solve for the position and orientation of frame {6}. The orientation of frame {6} w. r. t. frame {0} is defined by the rotational matrix: The translation of the origin of frame {6} w. r. t. frame {0} is defined by the vector

Inverse Kinematics We are now given the desired orientation and position of frame {6}, i. e. We now want to solve for all the joint angles ( 1, 2, 3, 4, 5, and 6)

Inverse Kinematics We are now given the desired orientation and position of frame {6}, i. e. We now want to solve for all the joint angles ( 1, 2, 3, 4, 5, and 6). First, we get the following:
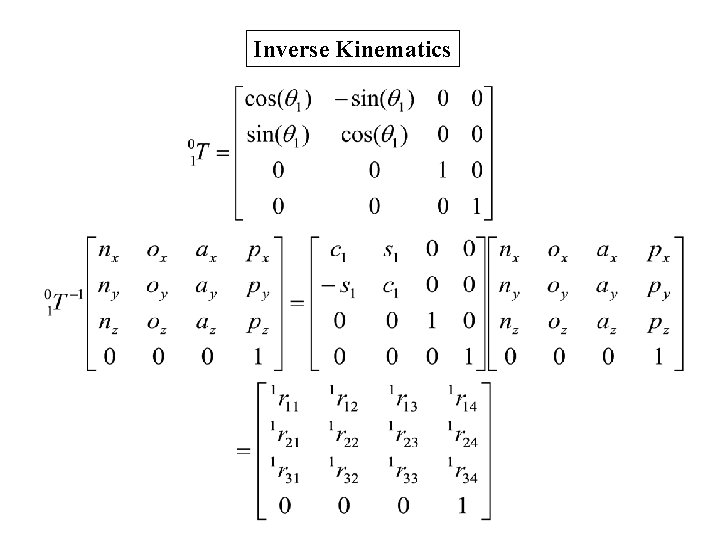
Inverse Kinematics

Inverse Kinematics Equate elements (2, 4) from both sides: Let Therefore where

Inverse Kinematics Equate elements (1, 4), (2, 4) and (3, 4) from both sides: Square all equations and add them to get:
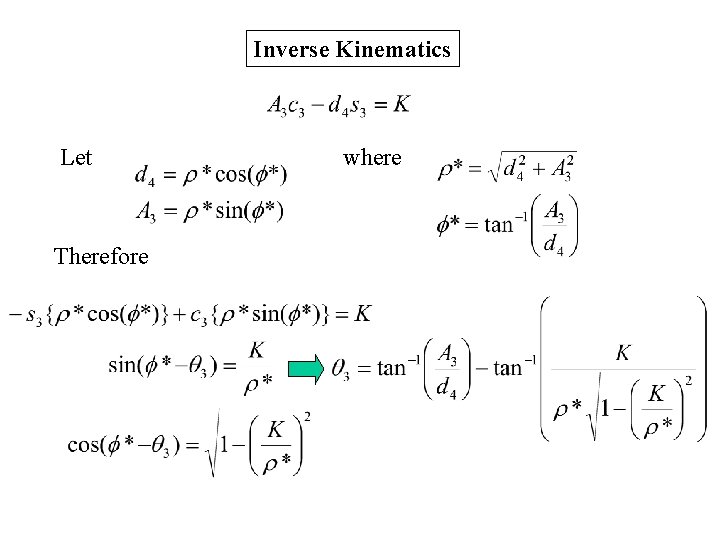
Inverse Kinematics Let Therefore where

Inverse Kinematics

Inverse Kinematics

Inverse Kinematics

Inverse Kinematics Equate elements (1, 4) and (2, 4) from both sides: Rearranging: We can solve for ( 2+ 3) from the above two equations:

Inverse Kinematics Equate elements (1, 3) and (3, 3) from both sides: Provided s 5 0

Inverse Kinematics

Inverse Kinematics Equate elements (1, 3) and (3, 3) from both sides:

Inverse Kinematics To find 6, we use Equate elements (1, 1) and (3, 1) from both sides:

Inverse Kinematics Given the orientation and position of frame {6}, i. e. given all the joint angles ( 1, 2, 3, 4, 5, and 6) can be found.

Summary This lecture continues the discussion on the analysis of the forward and inverse kinematics of robots. The following were covered: • Robot forward and inverse kinematics analysis using transformation matrices
- Slides: 28