Kinematic Graphs Graphically exploring derivatives and integrals 12292021

Kinematic Graphs Graphically exploring derivatives and integrals 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 1

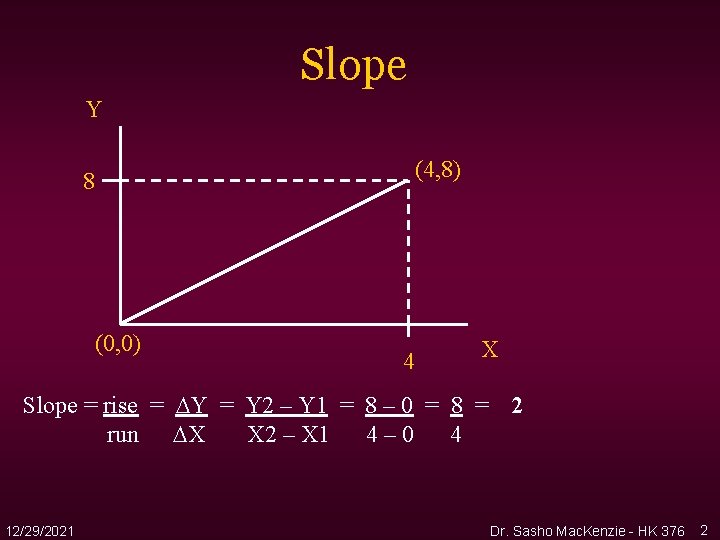
Slope Y (4, 8) 8 (0, 0) 4 X Slope = rise = Y 2 – Y 1 = 8 – 0 = 8 = run X X 2 – X 1 4– 0 4 12/29/2021 2 Dr. Sasho Mac. Kenzie - HK 376 2

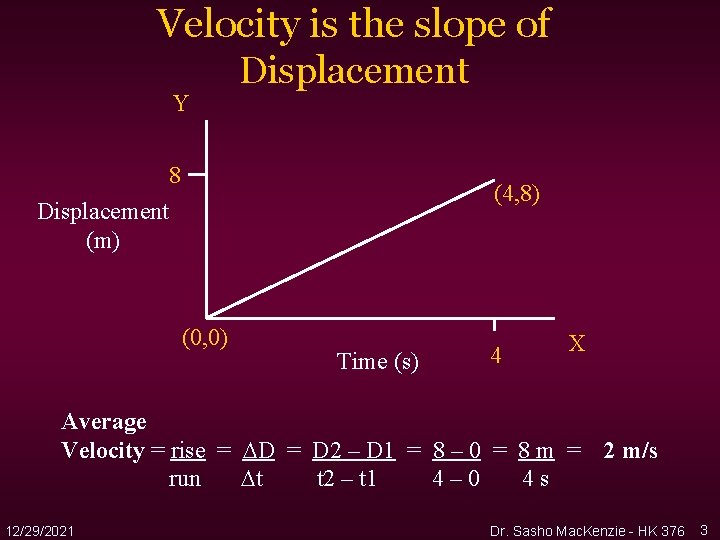
Velocity is the slope of Y Displacement 8 (4, 8) Displacement (m) (0, 0) Time (s) 4 X Average Velocity = rise = D 2 – D 1 = 8 – 0 = 8 m = run t t 2 – t 1 4– 0 4 s 12/29/2021 2 m/s Dr. Sasho Mac. Kenzie - HK 376 3

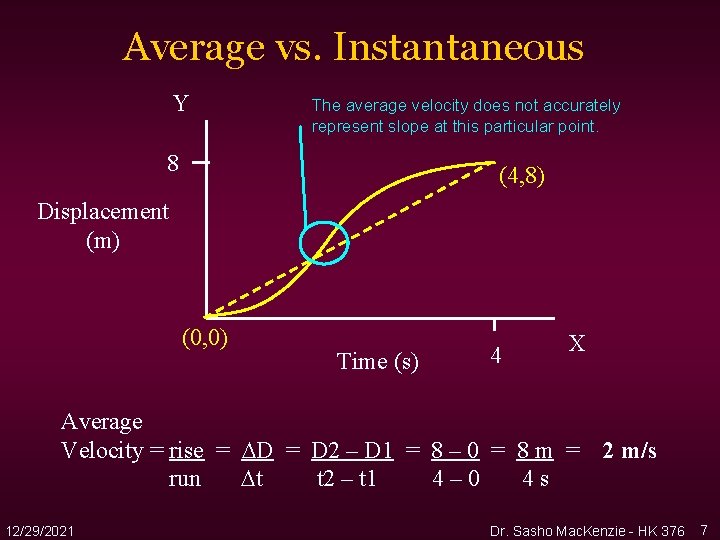
1. The displacement graph on the previous slide was a straight line, therefore the slope was 2 at every instant. 2. Which means the velocity at any instant is equal to the average velocity. 3. However if the graph was not straight the instantaneous velocity could not be determined from the average velocity 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 4

Instantaneous Velocity • The average velocity over an infinitely small time period. • Determined using Calculus • The derivative of displacement • The slope of the displacement curve 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 5

Instantaneous Acceleration • The average acceleration over an infinitely small time period. • Determined using Calculus • The derivative of velocity • The slope of the velocity curve 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 6

Average vs. Instantaneous Y The average velocity does not accurately represent slope at this particular point. 8 (4, 8) Displacement (m) (0, 0) Time (s) 4 X Average Velocity = rise = D 2 – D 1 = 8 – 0 = 8 m = run t t 2 – t 1 4– 0 4 s 12/29/2021 2 m/s Dr. Sasho Mac. Kenzie - HK 376 7

Derivative • The slope of the graph at a single point. • Slope of the line tangent to the curve. • The limiting value of D/ t as t approaches zero. 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 8

Infinitely small time period (dt) • Tangent line • Instantaneous Velocity Displacement dt t 3 t 2 t 1 Time 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 9

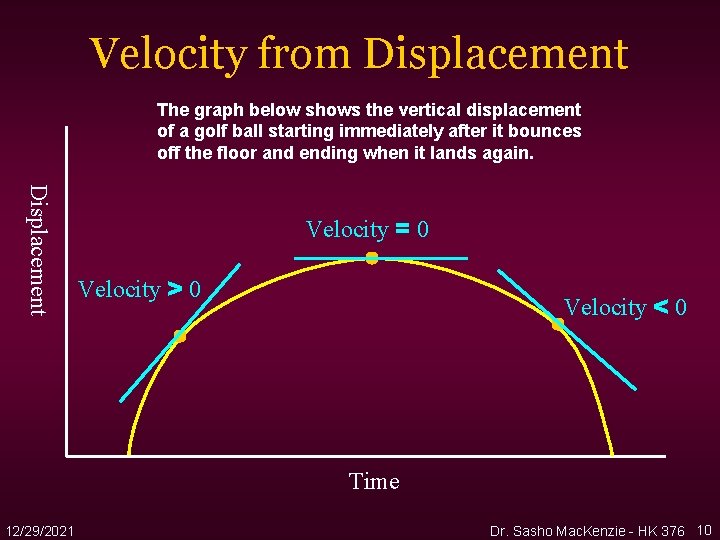
Velocity from Displacement The graph below shows the vertical displacement of a golf ball starting immediately after it bounces off the floor and ending when it lands again. Displacement Velocity = 0 Velocity > 0 Velocity < 0 Time 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 10

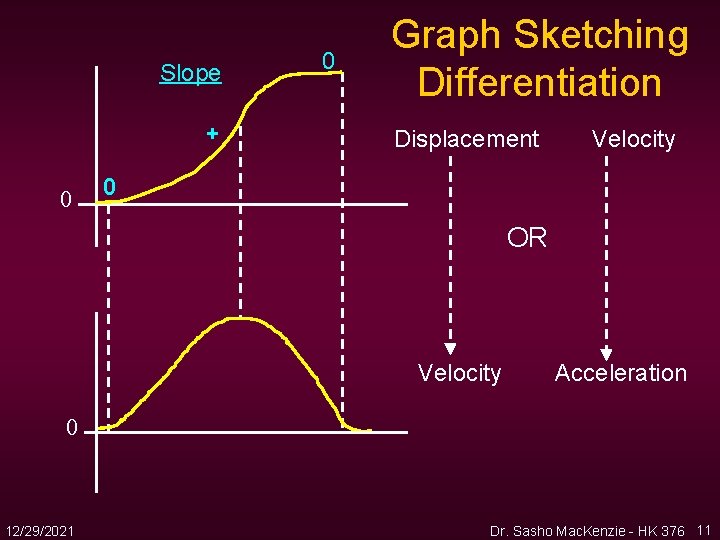
Slope + 0 0 Graph Sketching Differentiation Displacement Velocity 0 OR Velocity Acceleration 0 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 11

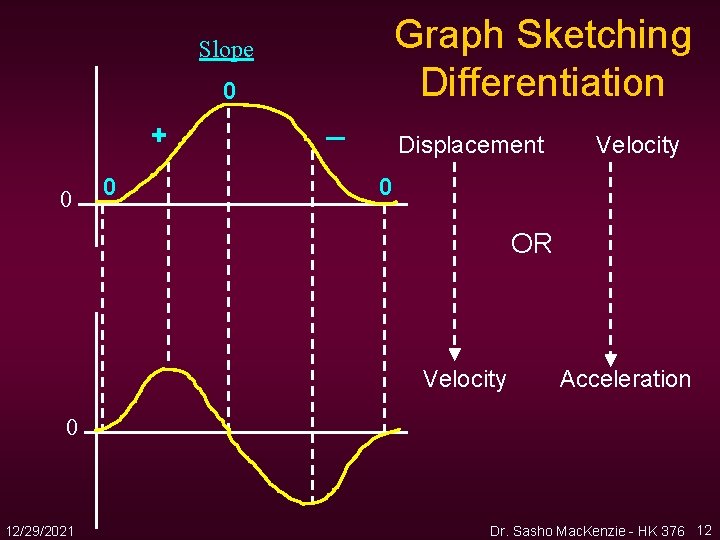
Graph Sketching Differentiation Slope 0 + 0 0 _ Displacement Velocity 0 OR Velocity Acceleration 0 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 12

Going the other way: area under the curve Y (2, 4) 4 (0, 0) 2 X Area under curve = Height x Base = Y x X = 4 x 2 = 8 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 13

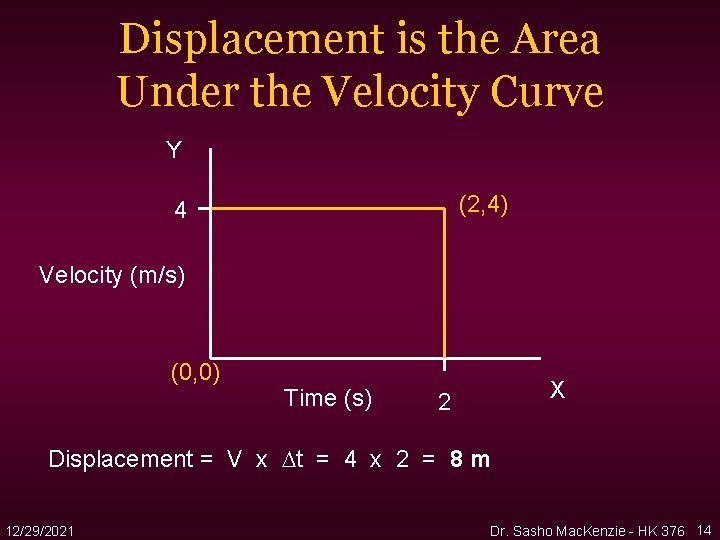
Displacement is the Area Under the Velocity Curve Y (2, 4) 4 Velocity (m/s) (0, 0) Time (s) X 2 Displacement = V x t = 4 x 2 = 8 m 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 14

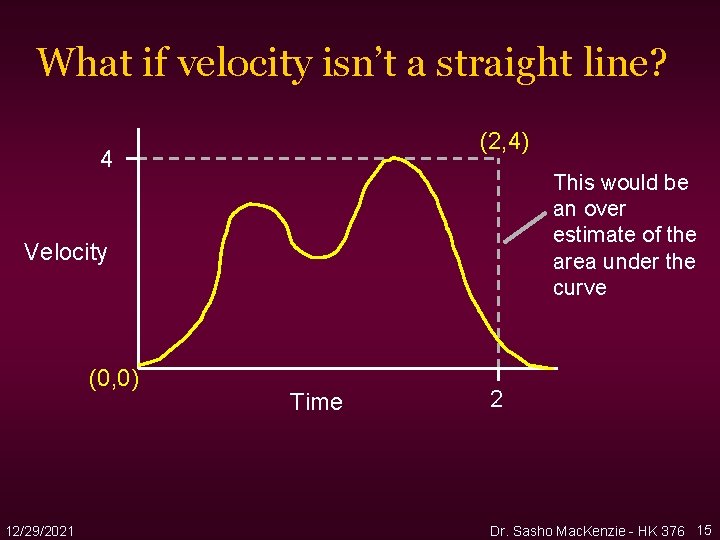
What if velocity isn’t a straight line? (2, 4) 4 This would be an over estimate of the area under the curve Velocity (0, 0) 12/29/2021 Time 2 Dr. Sasho Mac. Kenzie - HK 376 15

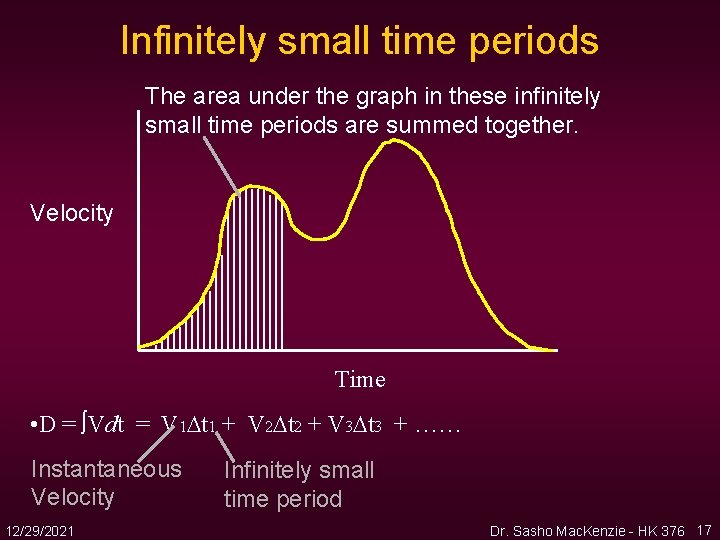
Integration • Finding the area under a curve. • Uses infinitely small time periods. • All the areas under the infinitely small time periods are then summed together. • D = Vdt = V t 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 16

Infinitely small time periods The area under the graph in these infinitely small time periods are summed together. Velocity Time • D = Vdt = V 1 t 1 + V 2 t 2 + V 3 t 3 + …… Instantaneous Velocity 12/29/2021 Infinitely small time period Dr. Sasho Mac. Kenzie - HK 376 17

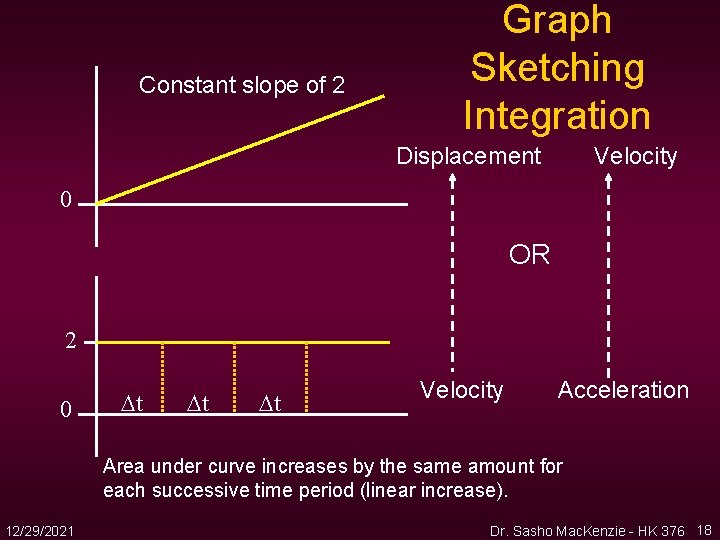
Constant slope of 2 Graph Sketching Integration Displacement Velocity 0 OR 2 0 t t t Velocity Acceleration Area under curve increases by the same amount for each successive time period (linear increase). 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 18

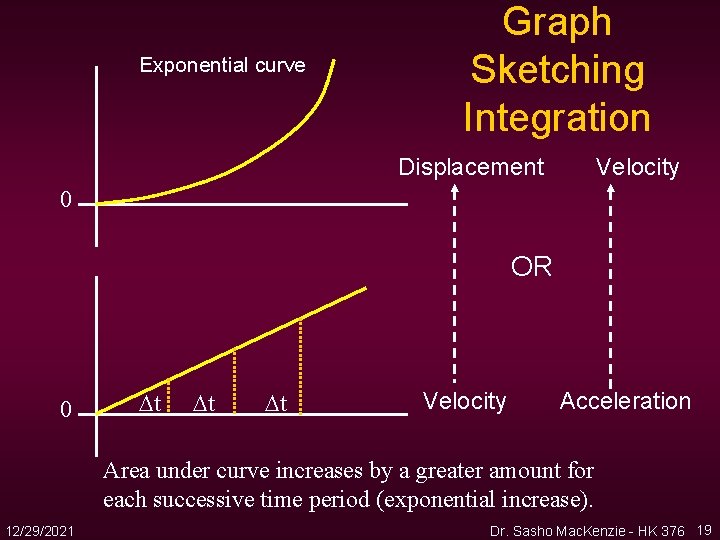
Exponential curve Graph Sketching Integration Displacement Velocity 0 OR 0 t t t Velocity Acceleration Area under curve increases by a greater amount for each successive time period (exponential increase). 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 19

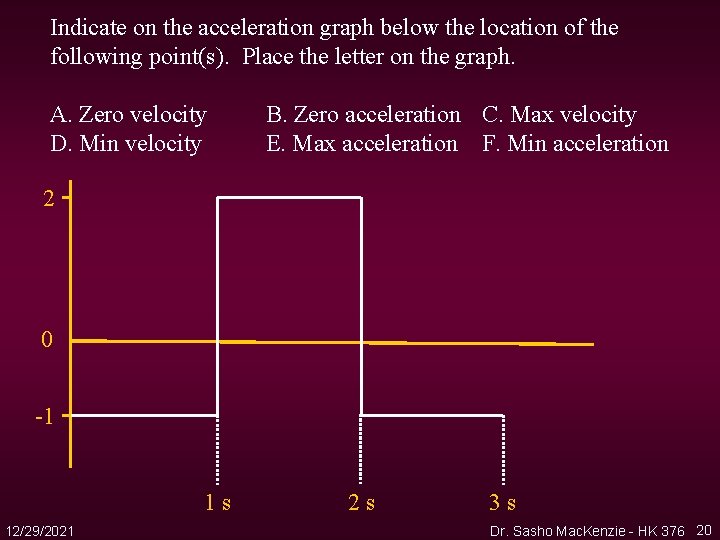
Indicate on the acceleration graph below the location of the following point(s). Place the letter on the graph. A. Zero velocity D. Min velocity B. Zero acceleration C. Max velocity E. Max acceleration F. Min acceleration 2 0 -1 1 s 12/29/2021 2 s 3 s Dr. Sasho Mac. Kenzie - HK 376 20

Indicate on the velocity graph below the location of the following point(s). Place the letter on the graph. A. Zero velocity D. Min velocity G. Max displacement B. Zero acceleration E. Max acceleration H. Min displacement C. Max velocity F. Min acceleration 0 12/29/2021 Dr. Sasho Mac. Kenzie - HK 376 21