Kim tra bi c Kim tra bi c

Kiểm tra bài cũ
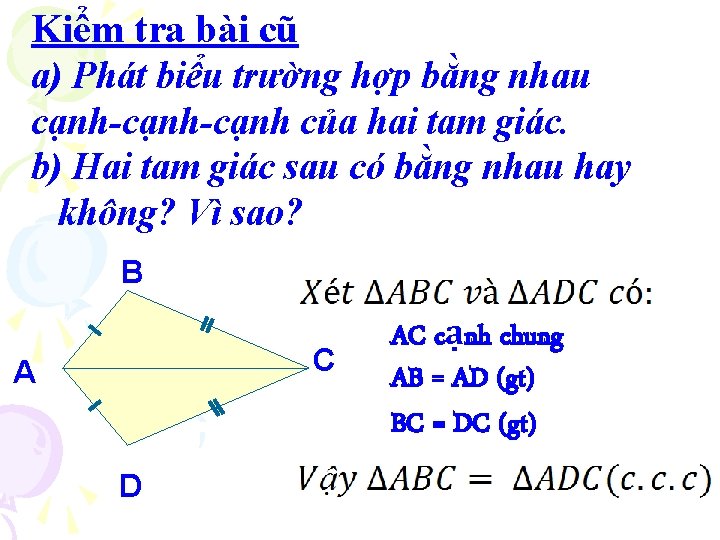
Kiểm tra bài cũ a) Phát biểu trường hợp bằng nhau cạnh-cạnh của hai tam giác. b) Hai tam giác sau có bằng nhau hay không? Vì sao? B C A D AC cạnh chung AB = AD (gt) BC = DC (gt)
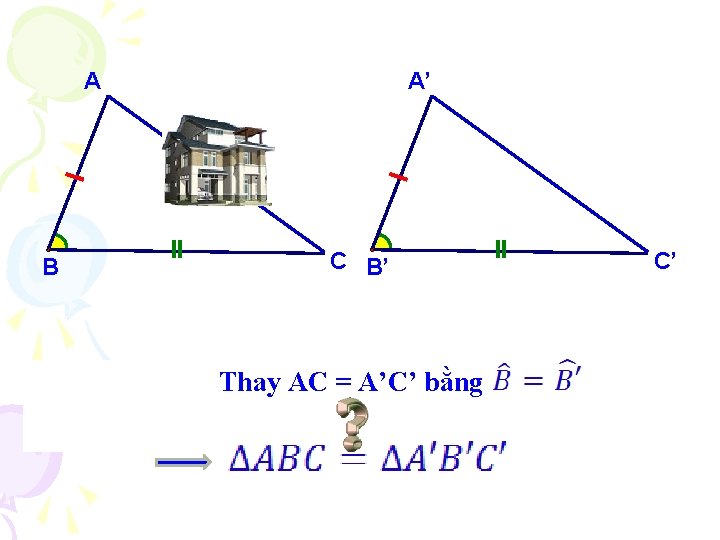
A B A’ C B’ Thay AC = A’C’ bằng C’

Tiết 25 § 4. TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC: CẠNH – GÓC – CẠNH
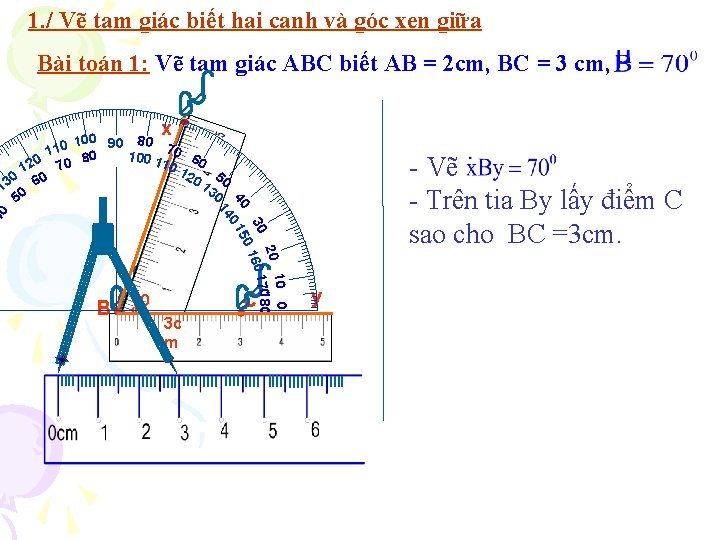
1. / Vẽ tam giác biết hai cạnh và góc xen giữa Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, x 40 B 70 0 3 c m 10 0 20 180 30 160 170 0 40 0 15 14 100 90 80 77 110 80 100 1 00 60 0 10 70 12 12 0 0 0 1 50 13 0 6 30 5 C - Vẽ - Trên tia By lấy điểm C sao cho BC =3 cm. y
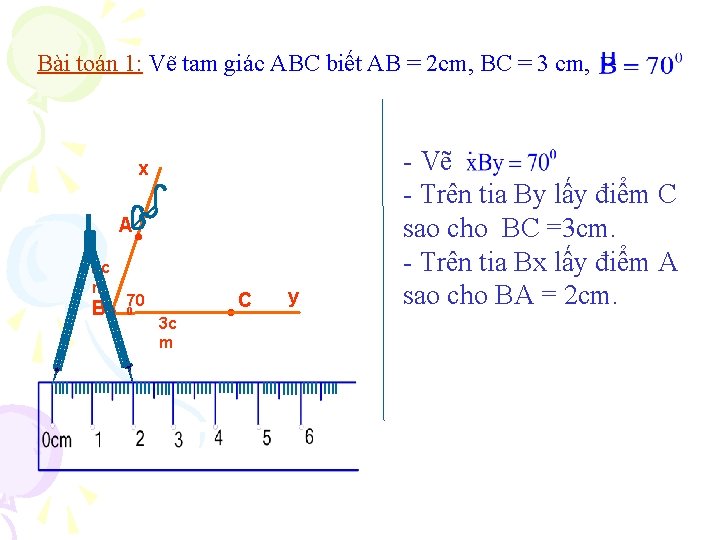
Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, x A 2 c m B C 70 0 3 c m y - Vẽ - Trên tia By lấy điểm C sao cho BC =3 cm. - Trên tia Bx lấy điểm A sao cho BA = 2 cm.
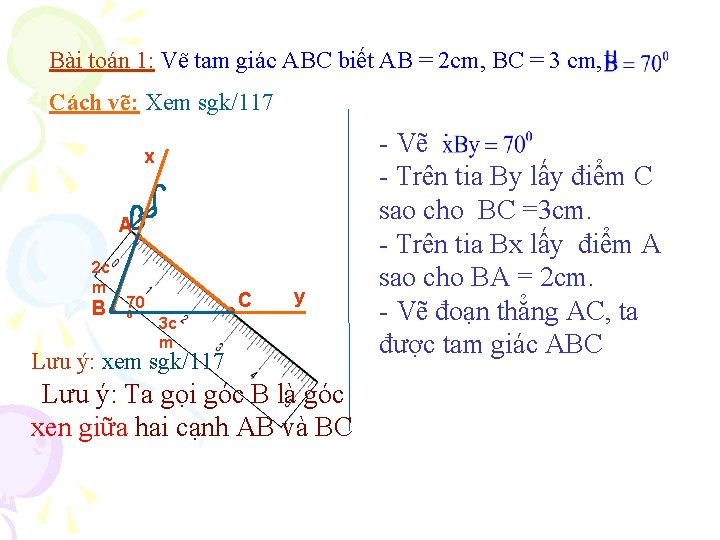
Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, Cách vẽ: Xem sgk/117 x A 2 c m B C 70 0 y 3 c m Lưu ý: xem sgk/117 Lưu ý: Ta gọi góc B là góc xen giữa hai cạnh AB và BC - Vẽ - Trên tia By lấy điểm C sao cho BC =3 cm. - Trên tia Bx lấy điểm A sao cho BA = 2 cm. - Vẽ đoạn thẳng AC, ta được tam giác ABC
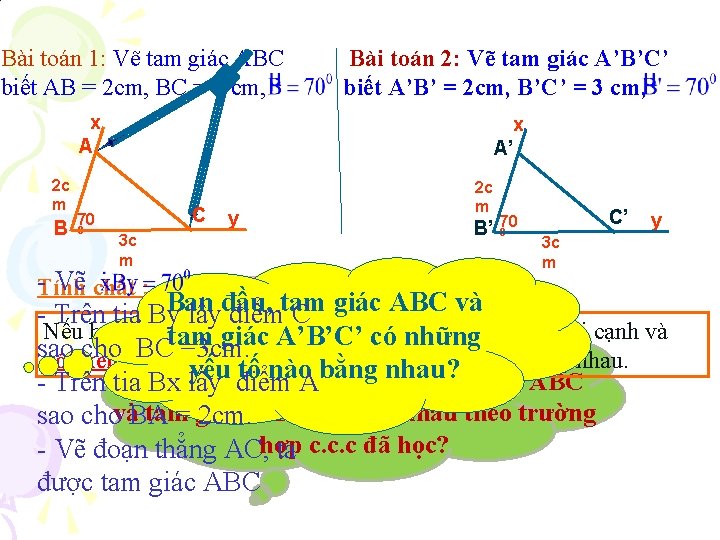
Bài toán 1: Vẽ tam giác ABC biết AB = 2 cm, BC = 3 cm, Bài toán 2: Vẽ tam giác A’B’C’ biết A’B’ = 2 cm, B’C’ = 3 cm, x A 2 c m B x A’ C 70 0 3 c m y 2 c m B’ C’ 70 0 3 c m y -Tính Vẽ chất : Ban tam Hãy đogiác và so. ABC sánh và = A’C’ - Trên tia By lấyđầu, điểm CAC Nếu hai cạnhtam và góc xen. A’B’C’ giữavới của. A’C’ tamnhững giác này bằng hai cạnh và giác có AC sao BC của =3 cm. góc cho xen giữa tam giác kia thì hai tam giác đó bằng nhau. yếu tố nào bằng nhau? Cần điều kiện - Trên tia Bxthêm lấy điểm A nào để tam giác ABC tam sao chovàBA = giác 2 cm. A’B’C’ bằng nhau theo trường - Vẽ đoạn thẳng AC, hợp ta c. c. c đã học? được tam giác ABC
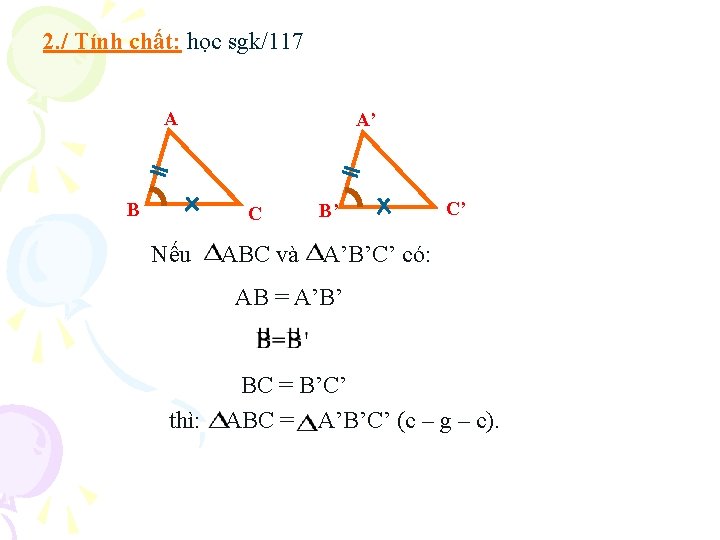
2. / Tính chất: học sgk/117 A B A’ C Nếu ABC và B’ C’ A’B’C’ có: AB = A’B’ BC = B’C’ thì: ABC = A’B’C’ (c – g – c).
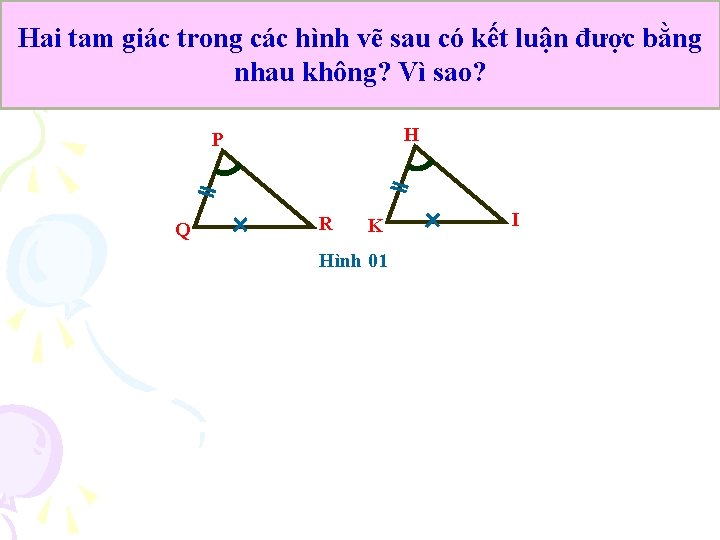
Hai tam giác trong các hình vẽ sau có kết luận được bằng nhau không? Vì sao? H P Q R K Hình 01 I
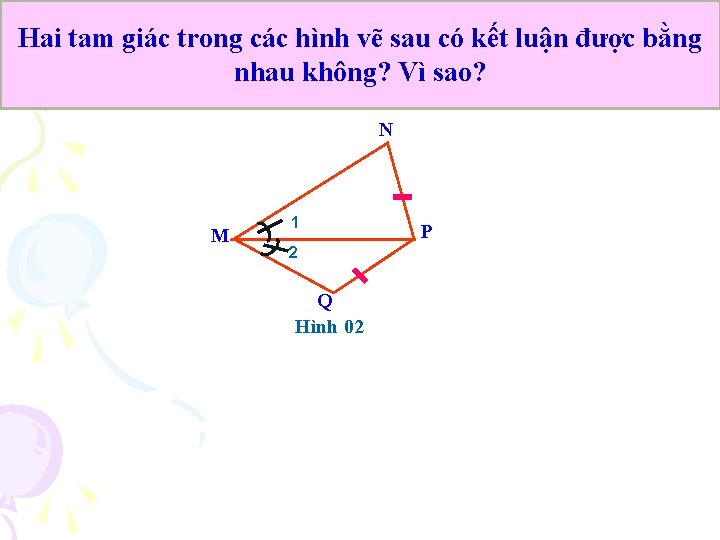
Hai tam giác trong các hình vẽ sau có kết luận được bằng nhau không? Vì sao? N M 1 2 Q Hình 02 P
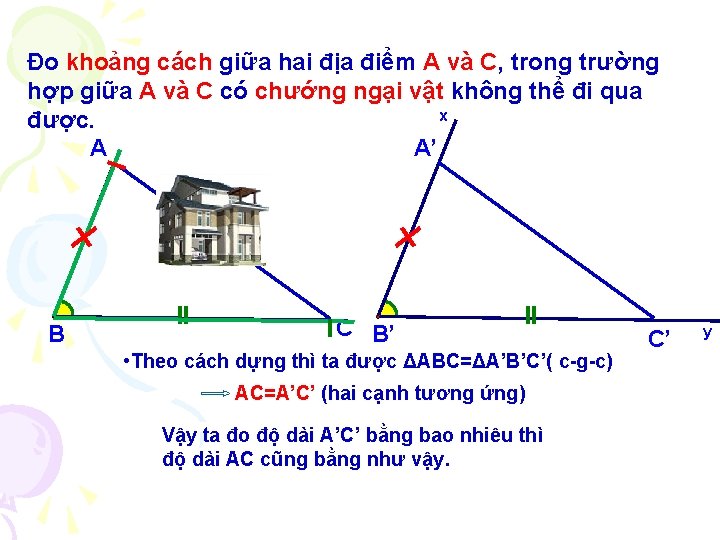
Đo khoảng cách giữa hai địa điểm A và C, trong trường hợp giữa A và C có chướng ngại vật không thể đi qua x được. A A’ B C B’ • Theo cách dựng thì ta được ΔABC=ΔA’B’C’( c-g-c) AC=A’C’ (hai cạnh tương ứng) Vậy ta đo độ dài A’C’ bằng bao nhiêu thì độ dài AC cũng bằng như vậy. C’ y
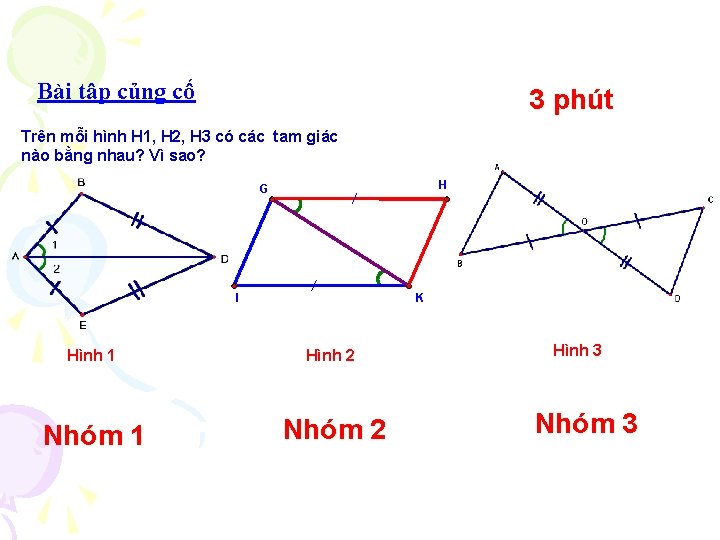
Bài tập củng cố 3 phút Trên mỗi hình H 1, H 2, H 3 có các tam giác nào bằng nhau? Vì sao? H G I Hình 1 Nhóm 1 K Hình 2 Nhóm 2 Hình 3 Nhóm 3
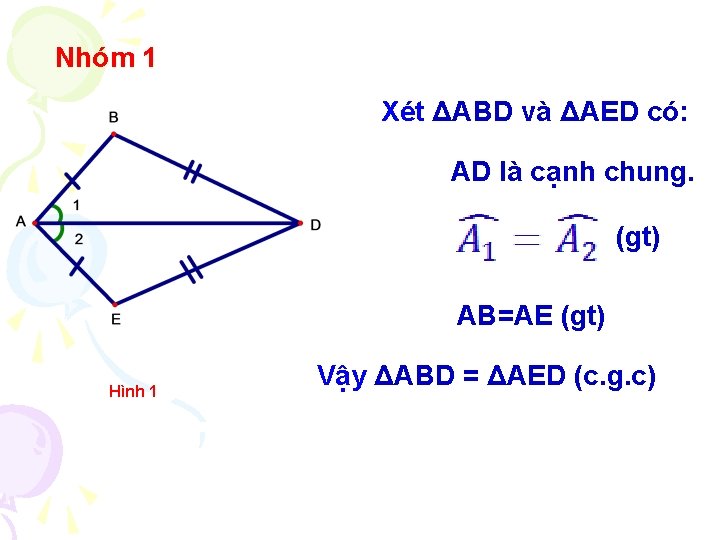
Nhóm 1 Xét ΔABD và ΔAED có: AD là cạnh chung. (gt) AB=AE (gt) Hình 1 Vậy ΔABD = ΔAED (c. g. c)
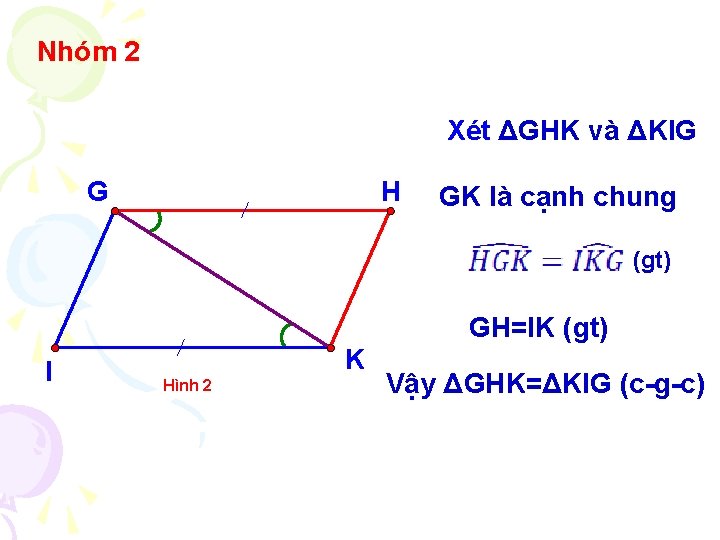
Nhóm 2 Xét ΔGHK và ΔKIG G H GK là cạnh chung (gt) GH=IK (gt) I K Hình 2 Vậy ΔGHK=ΔKIG (c-g-c)
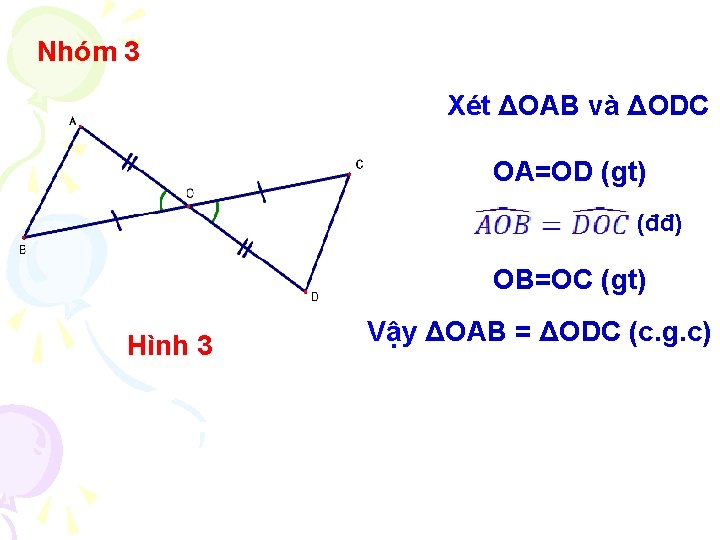
Nhóm 3 Xét ΔOAB và ΔODC OA=OD (gt) (đđ) OB=OC (gt) Hình 3 Vậy ΔOAB = ΔODC (c. g. c)
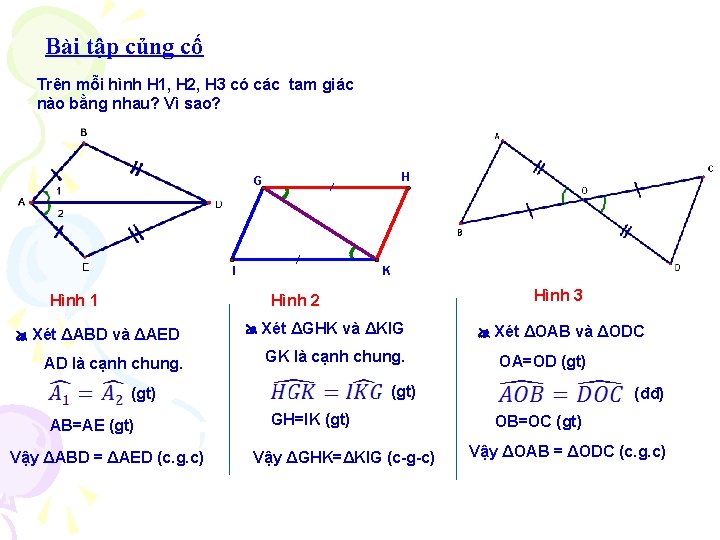
Bài tập củng cố Trên mỗi hình H 1, H 2, H 3 có các tam giác nào bằng nhau? Vì sao? H G I Hình 1 K Hình 3 Hình 2 Xét ΔABD và ΔAED Xét ΔGHK và ΔKIG AD là cạnh chung. GK là cạnh chung. Vậy ΔABD = ΔAED (c. g. c) OA=OD (gt) AB=AE (gt) Xét ΔOAB và ΔODC GH=IK (gt) Vậy ΔGHK=ΔKIG (c-g-c) (đđ) OB=OC (gt) Vậy ΔOAB = ΔODC (c. g. c)
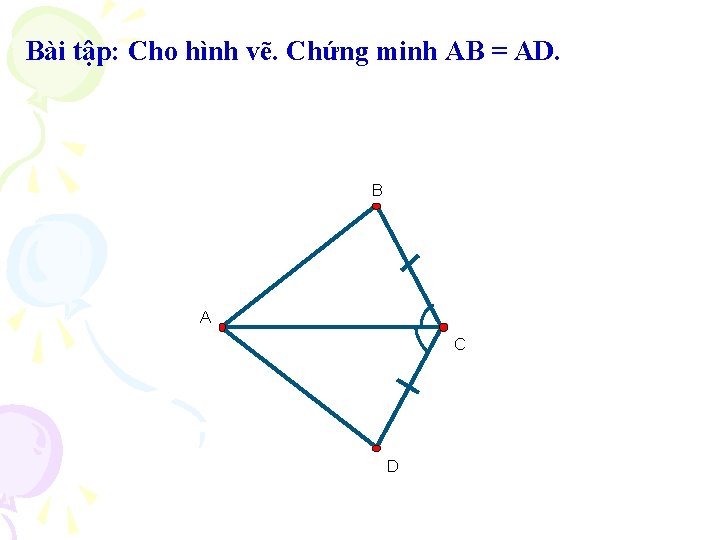
Bài tập: Cho hình vẽ. Chứng minh AB = AD. B A C D
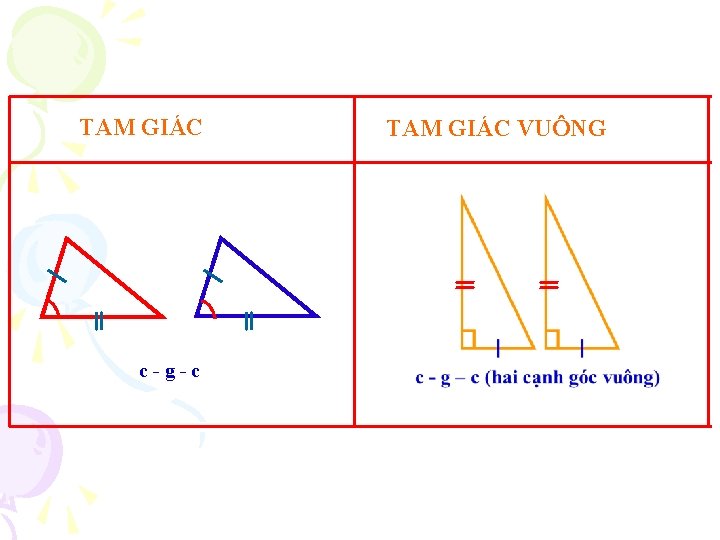
TAM GIÁC c-g-c TAM GIÁC VUÔNG

HƯỚNG DẪN VỀ NHÀ - Học thuộc tính chất về trường hợp bằng nhau thứ hai của tam giác và hệ quả trường hợp bằng nhau của hai tam giác vuông. - Làm bài tập 24, 26, 27 sgk/118 -119.
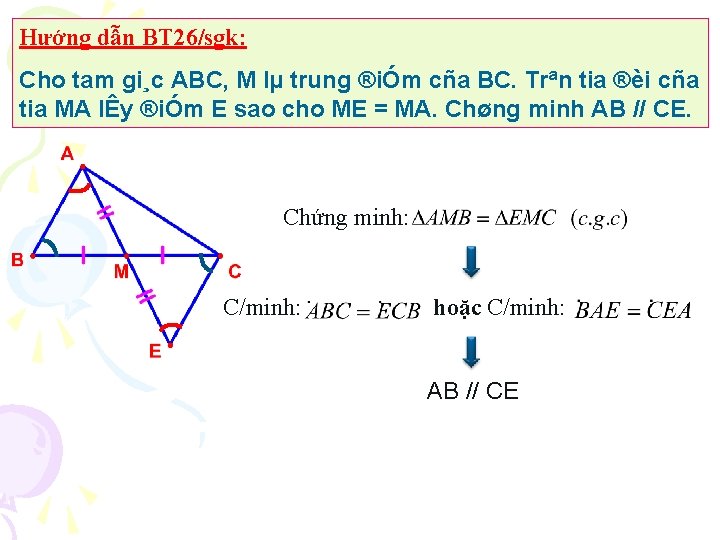
Hướng dẫn BT 26/sgk: Cho tam gi¸c ABC, M lµ trung ®iÓm cña BC. Trªn tia ®èi cña tia MA lÊy ®iÓm E sao cho ME = MA. Chøng minh AB // CE. Chứng minh: C/minh: hoặc C/minh: AB // CE
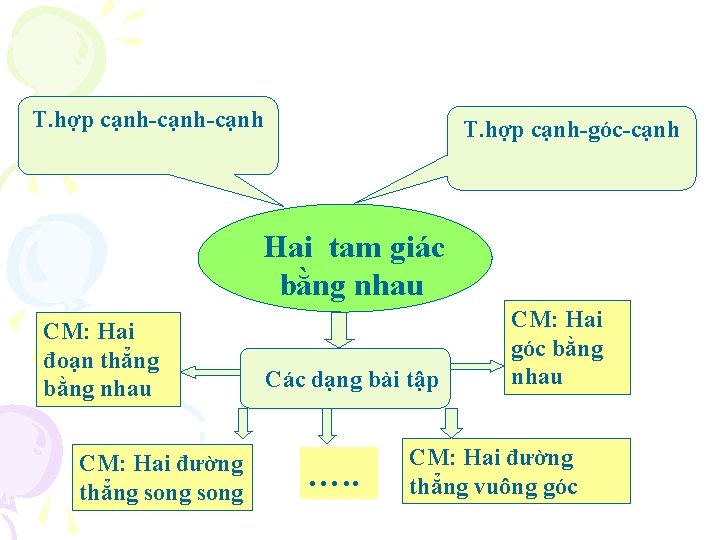
T. hợp cạnh-cạnh T. hợp cạnh-góc-cạnh Hai tam giác bằng nhau CM: Hai đoạn thẳng bằng nhau CM: Hai đường thẳng song Các dạng bài tập …. . CM: Hai góc bằng nhau CM: Hai đường thẳng vuông góc
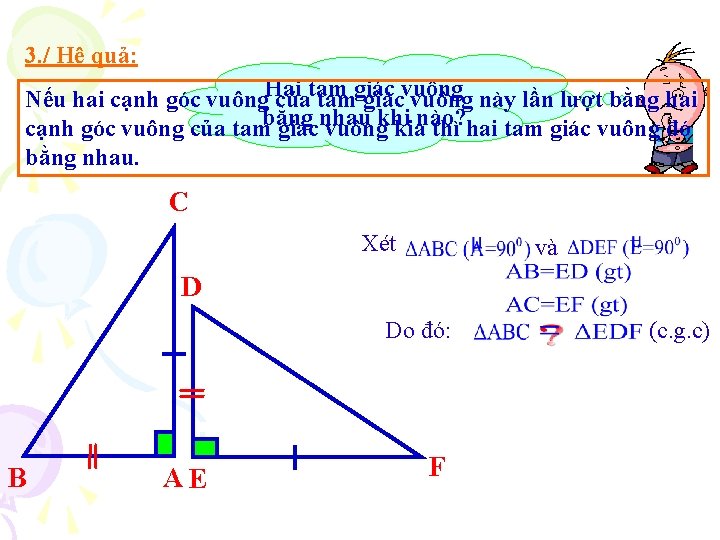
3. / Hệ quả: Nếu hai cạnh góc vuông. Hai củatam tamgiácvuông này lần lượt bằng hai cạnh góc vuông của tambằng giácnhau vuôngkhi kianào? thì hai tam giác vuông đó bằng nhau. C Xét và D Do đó: B AE F (c. g. c)



- Slides: 26