KIM TRA BI C HS 1 Phn tch


KIỂM TRA BÀI CŨ HS 1. Phân tích đa thức HS 2. Tính nhanh giá trị của sau thành nhân tử x 3 + 2 x 2 + x Đáp án x 3 + 2 x 2 + x biểu thức 872 + 732 -272 -132 Đáp án = x(x 2 + 2 x + 1) = x(x + 1)2 C¸ch 1: 872 + 732 -272 -132 = (872 – 272) +(732 – 132) = (87+27)(87 -27)+(73 -13)(73+13) = 114. 60 + 60. 86 = 60. (114 + 86) = 60. 200 = 12000

Tiết 11 PH N TÍCH ĐA THỨC THÀNH NH N TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ 1. Ví dụ 1 Phân tích đa thức sau thành nhân tử x 2 – 3 x + xy – 3 y - Các hạng tử có nhân. Giải tử chung hay không? )+ ( ) x 2 –-3 x 3 x + xy -3 y = ( - Làm thế nào để=xuất x(x –hiện 3) +nhân y(x tử - 3)chung? = (x – 3) (x + y)

Tiết 11 PH N TÍCH ĐA THỨC THÀNH NH N TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ 1. Ví dụ 2 Phân tích đa thức sau thành nhân tử x 2 – 2 xy + y 2 – 9 Giải - Các hạng tử 2 có nhân tử chung hay không? 2 -2 xy x – 2 xy ++y y --99 = ( ) = (x – y)2 - 32 - Làm thế nào để xuất hiện nhân tử chung? = (x –y – 3) (x –y + 3)

Tiết 11 PH N TÍCH ĐA THỨC THÀNH NH N TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ 1. Ví dụ 3 Phân tích đa thức sau thành nhân tử 2 xy + 3 z + 6 y + xz Giải )+( ) 2 xy + 3 z + 6 y + xz = ( = 2 y(x + 3) + z(x + 3) = (x + 3) (2 y + z) Cách làm như các ví dụ trên được gọi là phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử.

Tiết 11 PH N TÍCH ĐA THỨC THÀNH NH N TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ Xuất hiện nhân tử chung của ? . Em hiểu như thế nào là nhóm phân tích đa thức thành các Nhãm thÝch nhân tử bằng phương pháp nhóm hạng tử? hîp Xuất hiện hằng đẳng thức

Tiết 11 PH N TÍCH ĐA THỨC THÀNH NH N TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ 1. Ví dụ 2. Áp dụng ? 1 Tính nhanh 15. 64 + 25. 100 + 36. 15 60. 100 Giải 15. 64 + 25. 100 + 36. 15 60. 100 = (15. 64 + 36. 15) + (25. 100 + 60. 100) = 15. (64 + 36) + 100. (25 + 60) = 15. 100 + 100. 85 = 100. (15 + 85) = 100 = 10000

Tiết 11 PH N TÍCH ĐA THỨC THÀNH NH N TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ 1. Ví dụ 2. Áp dụng

? 2) Khi th¶o luËn nhãm mét b¹n ra ®Ò: H·y ph©n tÝch ®a thøc x 4 9 x 3 + x 2 9 x thµnh nh©n tö C¸c b¹n lµm nh sau: Th¸i: x 4 9 x 3 + x 2 9 x = x. (x 3 9 x 2 + x 9) Hµ: x 4 9 x 3 + x 2 9 x = ( x 4 9 x 3) + (x 2 9 x) = x 3. ( x 9) + x. (x 9) = ( x 9). (x 3 + x) An: x 4 9 x 3 + x 2 9 x = (x 4 + x 2) (9 x 3 + 9 x) = x 2. (x 2 + 1) 9 x. (x 2 + 1) = ( x 2 + 1). (x 2 9 x) = x. (x 9). (x 2 +1) H·y nªu ý kiÕn cña em vÒ lêi gi¶i cña c¸c b¹n? §¸p ¸n: C¶ ba b¹n ®Òu lµm ®óng, nh ngb¹n An lµm ®óng nhÊt cßn b¹n Th¸i vµ b¹n Hµ ph©n tÝch ch ahÕt

Bµi cña b¹n Th¸i ® îc gi¶i tiÕp nh sau: x 4 9 x 3 + x 2 9 x = x. (x 3 x 2 + x 9) =x. [(x 3 9 x 2) + (x 9)] = x. [x 2(x 9) + (x 9)] = x. (x 9). (x 2 +1) Bµi cña b¹n Hµ ® îc gi¶i tiÕp nh sau: x 4 9 x 3 + x 2 9 x = ( x 4 9 x 3) + (x 2 9 x) = x 3. ( x 9) + x. (x 9) = ( x 9). (x 3 + x) = ( x 9). x(x 2 + 1) = x. ( x 9). (x 2 + 1)

3) LuyÖn tËp: Bµi 47 c: Ph©n tÝch ®a thøc sau thµnh nh©n tö: §¸p ¸n: 3 x 2 3 xy 5 x + 5 y = (3 x 2 3 xy) (5 x 5 y) = 3 x(x y) 5(x y) = (x y). (3 x 5)
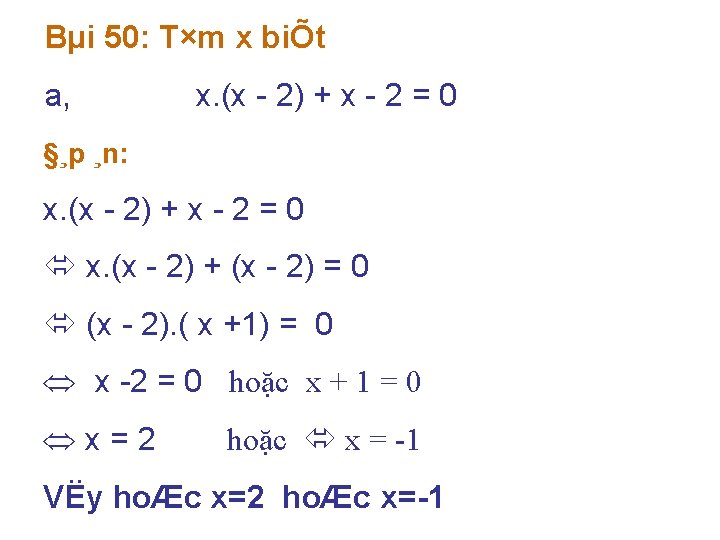
Bµi 50: T×m x biÕt a, x. (x 2) + x 2 = 0 §¸p ¸n: x. (x 2) + x 2 = 0 x. (x 2) + (x 2) = 0 (x 2). ( x +1) = 0 x 2 = 0 hoặc x + 1 = 0 x=2 hoặc x = -1 VËy hoÆc x=2 hoÆc x= 1

THỂ LỆ : Có 4 bông hoa với màu sắc khác nhau được ghi số (Từ số 1 đến số 4). Mỗi đội hãy chọn cho mình một bông hoa bất kì. Yêu cầu trả lời trong vòng 30 giây. Mỗi câu trả lời đúng được 10 điểm. Điểm được tính cho đồng đội.

2 1 3 4

H íngdÉn häc ë nhµ • ¤n tËp 3 ph ¬ngph¸p ph©n tÝch ®a thøc thµnh nh©n tö ®· häc • Bµi tËp vÒ nhµ: 48; 49; 50 b (SGK), 31, 32 ( SBT)

Back Phân tích đa thức thành nhân tử x 2 – xy + x – y Vì: x 2 – xy + x y a/ (x – y)(x + 1) = (x 2 – xy) + (x – y) b/ (x – y)(x 1) = x(x – y) + (x – y) c/ (x – y)(x + y) = (x – y)(x + 1) 46 28 14 19 26 23 27 13 12 11 10 18 17 16 15 22 21 20 25 24 30 29 4 3 2 1 0 9 8 7 6 5

Back Phân tích đa thức thành nhân tử xz + yz – 5(x + y) Vì: xz + yz – 5(x + y) a/ (x+ y)(z + 5) = (xz + yz) – 5(x + y) b/ (x + y)(x – z) = z(x + y) – 5(x + y) c/ (x + y)( z – 5) = (x + y)(z – 5) 46 28 14 19 26 23 27 13 12 11 10 18 17 16 15 22 21 20 25 24 30 29 4 3 2 1 0 9 8 7 6 5

Back Phân tích đa thức thành nhân tử: Vì: 3 x 2 – 3 xy – 5 x + 5 y a/ (x – y)(3 x – 5) = (3 x 2 – 3 xy) – (5 x – 5 y) b/ (x – y)(3 x + 5) = 3 x(x – y) – 5(x – y) c/ (x – y)(x – 5) = (x – y)(3 x – 5) 46 28 14 19 26 23 27 13 12 11 10 18 17 16 15 22 21 20 25 24 30 29 4 3 2 1 0 9 8 7 6 5

Back Phân tích đa thức thành nhân tử x 2 + 4 x + 4 – y 2 Vì: a/ (x +2)(x – 4) b/(x + 2 + y)(x +2 y) c/ x(x + 2) x 2 + 4 x + 4 – y 2 = (x 2 + 4 x + 4) – y 2 = (x + 2)2 – y 2 = (x +2 + y)(x + 2 – y) 46 28 14 19 26 23 27 13 12 11 10 18 17 16 15 22 21 20 25 24 30 29 4 3 2 1 0 9 8 7 6 5

- Slides: 20