KIM Kim tra TRA bi cBI C Mun

KIỂM Kiểm tra. TRA bài cũBÀI CŨ Muốn tìm bội của một số khác 0 ta làm thế nào? 12 là bội chung nhỏ nhất Tìm B(4); B(6); BC(4; 6). của 4 và 6. Giải: B(4) = {0; 0 4; 8; 12 12; 16; 20; 24 24; 28; 32; 36 36; ………. . } B(6) = {0; 0 6; 12 12; 18; 24 24; 30; 36 36; ………………. } BC(4; 6) = {0; 12 12; 24; 36; ………. } Số 12 là số nhỏ nhất khác 0 trong tập hợp các bội chung của 4 và 6.

Ví dụ 1: 1. Béi chung nhá nhÊt Bài tập: Tìm: Ví dụ 1: Tìm tập hợp các bội chung của 4 và 6 Béi chung nhá nhÊt cña hai B(4)={0; 4; 8; 12; 16; 20; 24; 28; 32; a/BCNN(8, 1) hay nhiÒu sè lµ sè nhá nhÊt 36; …} B(6)0=trong {0; 6; 12; 18; 24; 30; kh¸c tËp hîp béi 36; …} chung Có cách nào tìm b/ BCNN(4, 6, 1) BC(4; {0; 12; 24; 36; …. . } cña c¸c 6) sè=®ã. Giải BCNN của hai hay Kí hiệu bội chung nhỏ nhất của a/ B(8) ={0; 8; 16; 24; 32; …} Kí hiệu : BCNN(4; 6) =12 B(1) ={0; 1; 2; 3; 4; 5; 6; 7; 8; 9; …} hai số a và b là : BCNN(a; b) nhiều số mà không uan. . . } NhËn xÐt : TÊt c¸c béi chung BC(8; 1) = {0; 8; Q 24; hệ ? cần liệt. BCNN(8; kê bội 1) = 8 cña 4 vµ 6 ( lµ 0, 12, 24 , 36, …) B(4)các = {0; số 4; 8; 12; 16; 20; 24; …. } ®Òu lµ béi chung b/ của B(6) = {0; 6; 12; 18; 24; 30; …. } cña BCNN (4, 6 ). Chó ý : Mọi số tự nhiên đều là hay bội B(1) không? = của 1. Do đó: Với mọi số tự nhiên a ={0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; . . } và b (khác 0) ta có: B(4; 6; 1) = {0; 12; 24; …. } BCNN( a, 1) = a BCNN(a, b, 1) = BCNN (a , BCNN(4; 6; 1) =12 = BCNN(4; 6) b)

1. Bội chung nhỏ nhất: 2. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố: Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau: Bước 1: Phân tích mỗi số ra thừa số nguyên tố. Bước 2: Chọn ra các thừa số nguyên tố chung và riêng. Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm. Ví dụ 2: Tìm BCNN (8; 18; 30) Bước 1: Phân tích mỗi số ra thừa số nguyên tố. 8 = 23 18 = 2. 32 30 = 2. 3. 5 Bước 3: Chọn ra các thừa số nguyên tố chung và riêng 2; 3; 5 Bước 3: Lập tích các thừa số đã chọn, Mỗi thừa số lấy với số mũ lớn nhất của nó. BCNN (8; 18; 30) =. . 5 = 360

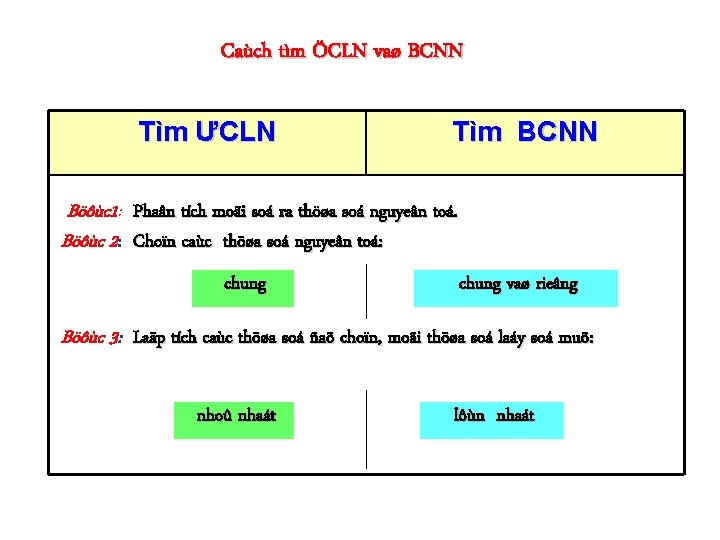
Caùch tìm ÖCLN vaø BCNN Tìm ƯCLN Tìm BCNN Böôùc 1: Phaân tích moãi soá ra thöøa soá nguyeân toá. Böôùc 2: Choïn caùc thöøa soá nguyeân toá: chung vaø rieâng Böôùc 3: Laäp tích caùc thöøa soá ñaõ choïn, moãi thöøa soá laáy soá muõ: nhoû nhaát lôùn nhaát

1. Béi chung nhá nhÊt a/ BCNN 12)phân tích 2. Tìm BCNN bằng(8; cách : các số ra thừa số nguyên tố: Tìm: b/ BCNN(5; 7; 8) c/ BCNN(12; 16; 48) 1/ Nếu các số đã cho từng đôi một Giải nguyên tố cùng nhau thì BCNN a/ 8 = 23 của chúng là tích của các số đó. 2. 3 12 = 2 Ví dụ: BCNN(5; 7; 8) = 5. 7. 8 = 280 BCNN(8; 12 ) = 23. 3 = 24 b/ 5 = 5 7=7 2/ Trong các số đã cho, nếu số lớn 8 = 23 nhất là bội của các số còn lại thì BCNN(5; 7; 8 )=23. 5. 7=8. 5. 7 BCNN của chúng là số lớn nhất =c/280 12 = ấy. 2216. 3 = Ví dụ: BCNN(12; 16; 48) = 48. . 3 48 = BCNN(12; 14; 48) =. 3 = 48

Béi chung nhá nhÊt cña hai hay nhiÒu sè lµ sè nhá nhÊt 1. Bội 0 chung kh¸c trongnhỏ tËpnhất: hîp béi chung cña c¸c sè ®ã. Kí hiệu bội chung nhỏ nhất của hai số a và b là : BCNN(a; b) Chú ý: BCNN( a , 1) = a BCNN( a, b , 1) = 2 BCNN. Tìm bội ( a , chung b) nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố: Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước : Bước 1: Phân tích mỗi số ra thừa số nguyên tố. Bước 2: Chọn ra các thừa số nguyên tố chung và riêng. Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm. Chú ý: 1/ Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó. 2/ Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của chúng là số lớn nhất ấy.

BÀI TẬP 1/ Tìm BCNN cña : a) 60 vµ 280 c) 13 vµ 15 b) 40 ; 28 ; 140 d/ 24; 40 ; 168 81 7 6 5 4 3 1 18 20 2 28 0 10 42 13 16 36 38 40 45 1 12 14 21 25 24 27 35 34 33 32 31 30 37 44 43 9 15 17 19 22 26 29 39 41 3 Giải a) 60 vµ 280 60 = 22. 3. 5 280 = 2; 3. 5. 7 BCNN(60, 280) = 23. 3. 5. 7 = 840 b) 40 ; 28 ; 140 40 = 23. 5 28 = 22. 7 140 = 22. 5. 7 BCNN(40; 28; 140) 2=3. 5. 7 = 8. 5. 7 = 280 c) 13 vµ 15 BCNN(13; 15) =13. 15 = 195 d/ 30; 150 BCNN( 30; 150) = 150

BOÄI CHUNG NHOÛ NHAÁT ? . Ñoïc soá em choïn ñeå ñöôïc keát quaû ñuùng : Trong dòp thi ñua laäp thaønh tích chaøo möøng 20 – 11 ñeå ñoäng vieân caùc hoïc sinh coù thaønh tích cao trong hoïc taäp, coâ giaùo ñaõ mua moät soá quyeån vôû vaø döï ñònh chia ñeàu ra caùc phaàn thöôûng. Haõy tính soá quyeån vôû coâ giaùo ñaõ mua, bieát raèng ñoù laø moät soá töï nhieân nhoû nhaát khaùc 0 maø khi chia laøm 2 phaàn thöôûng, RÊttiÕcb¹n b¹ntr¶ tr¶lêi lêisai sairåi RÊt tiÕc 4 phaàn thöôûng, 5 phaàn thöôûng ñeàub¹n vöøa ñuû. råi !! ! 10 12 60 Chóc mõng b¹n ®· cã c©u tr¶ lêi ®óng ! Soá quyeån vôû coâ giaùo ñaõ mua laø : …. …… ………quyeån 20 20

- Xem muïc “III. Caùch tìm boäi chung thoâng qua tìm BCNN “ - Hoïc lyù thuyeát nhö sgk vaø laøm baøi taäp: 149(b) , 150 (a, b), 151 SGK trang 59.

Tạm biệt quyù thaày giaùo, coâ giaùo cuøng caùc em hoïc sinh. Xin chân thành cảm ơn !