kili Aalar kili Arama Aalar H Qunun sunumlarndan

İkili Ağaçlar İkili Arama Ağaçları H. Qu’nun sunumlarından tercüme edilerek uyarlanmıştır.

Ağaçlar * Bağlantılı listedeki erişim zamanı lineerdir. Çoğu işlemlerin (operasyon) (arama, ekleme, silme) çalışma zamanını daha aza indiren (O(log N) gibi) başka bir veri yapısı var mıdır? n

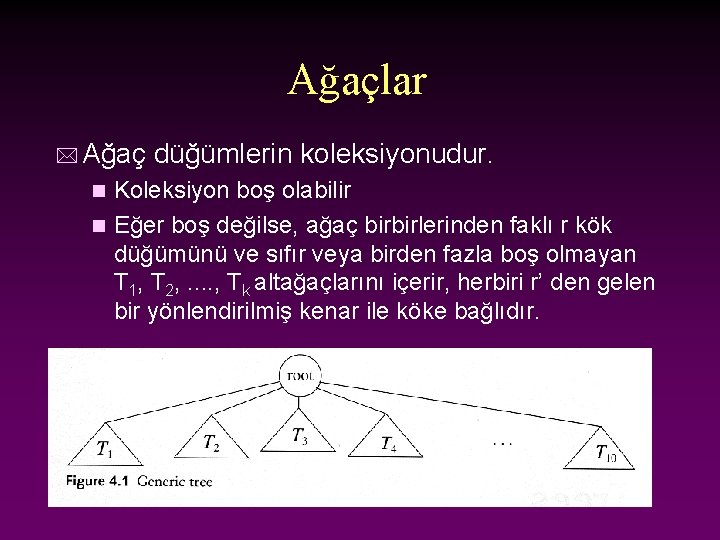
Ağaçlar * Ağaç düğümlerin koleksiyonudur. Koleksiyon boş olabilir n Eğer boş değilse, ağaç birbirlerinden faklı r kök düğümünü ve sıfır veya birden fazla boş olmayan T 1, T 2, . . , Tk altağaçlarını içerir, herbiri r’ den gelen bir yönlendirilmiş kenar ile köke bağlıdır. n

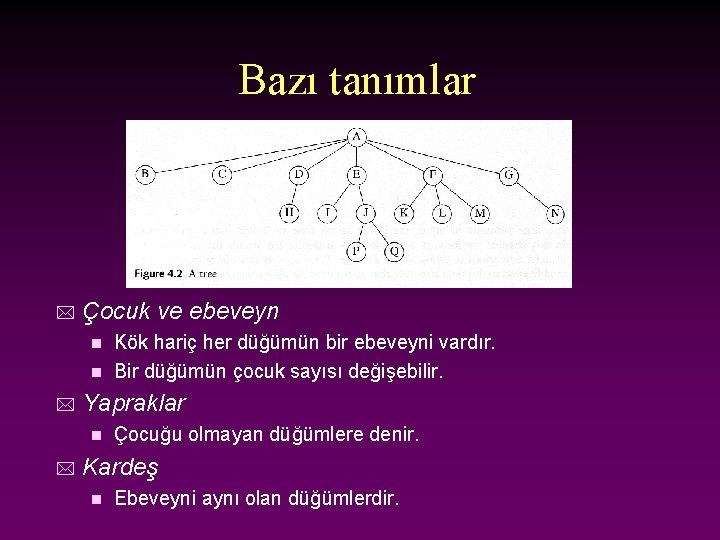
Bazı tanımlar * Çocuk ve ebeveyn Kök hariç her düğümün bir ebeveyni vardır. n Bir düğümün çocuk sayısı değişebilir. n * Yapraklar n * Çocuğu olmayan düğümlere denir. Kardeş n Ebeveyni aynı olan düğümlerdir.

Bazı Tanımlar Patika – yol - Path * Uzunluk - Length * n * Bir yoldaki kenar sayısı Bir düğümün derinliği Kökten düğüme olan tekil yolun uzunluğu n Bir ağacın derinliği en derinde bulunan yaprağın derinliğine eşittir. n * Bir düğümün yüksekliği Düğümden bir yaprağa olan en uzun yola denir. n Bütün yapraklar yükseklik 0 ‘ da bulunur n Bir ağacın yüksekliği kökün yüksekliğine eğittir. n * Ata (veya dede) ve torun

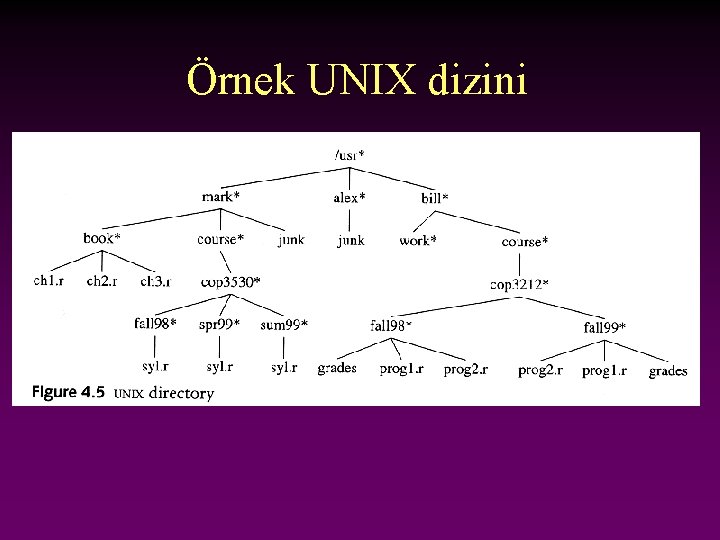
Örnek UNIX dizini

İkili Ağaçlar * Bu ağaçta hiçbir düğümün ikiden fazla çocuğu olamaz * Ortalama bir ikili ağacın derinliği N ‘den küçüktür, en kötü durumda bile derinlik N-1 olabilir.

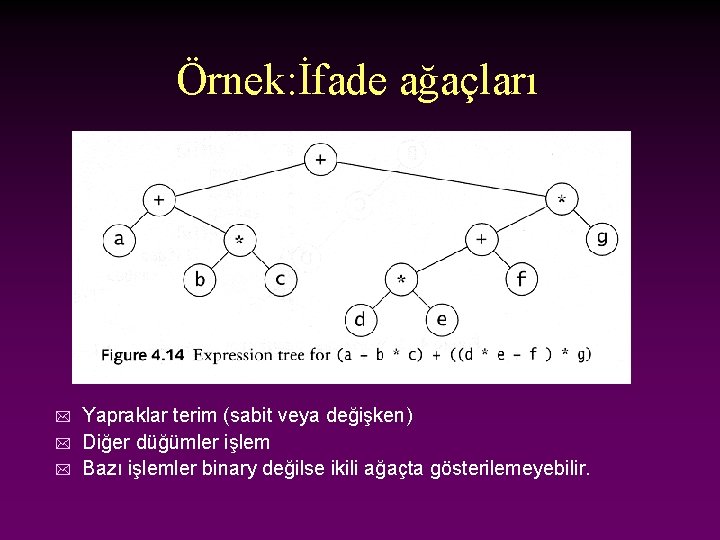
Örnek: İfade ağaçları * * * Yapraklar terim (sabit veya değişken) Diğer düğümler işlem Bazı işlemler binary değilse ikili ağaçta gösterilemeyebilir.

İfade Ağacından Eşitlik Çıkarma * * * Mümkün olduğunca alttan yukarı doğru eşitlik oluşturulur. Her alt ağaç bir parantez içidir. Ara işlem 1 (Eksinin sol tarafı) 3*7 (alt ağaç) n 4 + (3*7) (alt ağaç) n Eksinin sol tarafı tamamlandı. n * Ara işlem 2 (Eksinin sağ tarafı) 3 + 4 (alt ağaç) n 5 / (3 + 4) (alt ağaç) n Eksinin sağ tarafı tamamlandı. n * Ara işlem 3 (Kökün sol tarafı) (4+(3*7)) - (5/(3+4)) (alt ağaç) n Artının sol tarafı tamamlandı n * * Ara işlem 4 (Kökün sağ tarafında sayı var. ) Eşitliğin son hali * * (4+(3*7)) - (5/(3 + 4))) + 6 Bazı parantezleri kaldırabiliriz (4+3*7) – (5/(3+4)) + 6 veya n 4+3*7 – (5/(3+4)) + 6 n Kaynak: http: //cs. middlesexcc. edu/~schatz/csc 236/handouts/Trees. html

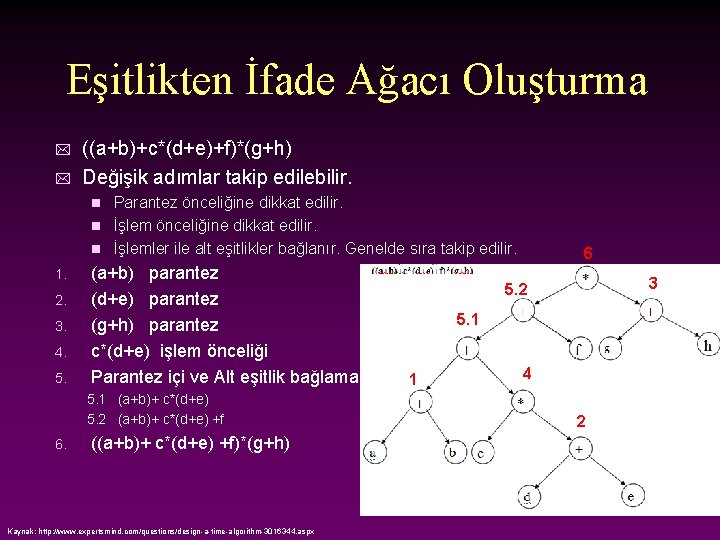
Eşitlikten İfade Ağacı Oluşturma * * ((a+b)+c*(d+e)+f)*(g+h) Değişik adımlar takip edilebilir. Parantez önceliğine dikkat edilir. n İşlemler ile alt eşitlikler bağlanır. Genelde sıra takip edilir. n 1. 2. 3. 4. 5. (a+b) parantez (d+e) parantez (g+h) parantez c*(d+e) işlem önceliği Parantez içi ve Alt eşitlik bağlama 5. 1 (a+b)+ c*(d+e) 5. 2 (a+b)+ c*(d+e) +f 6. ((a+b)+ c*(d+e) +f)*(g+h) Kaynak: http: //www. expertsmind. com/questions/design-a-time-algorithm-3016344. aspx 6 3 5. 2 5. 1 1 4 2

Ağaç Gezme (Tree Traversal) * Bir ağaçtaki verileri belli bir düzende yazmak için kullanılır. * Önce-kök Gezme (Pre-order traversal) Kökteki veriyi yaz n Sol altağaçtaki verileri iteratif olarak yaz n Sağ altağaçtaki verileri iteratif olarak yaz n

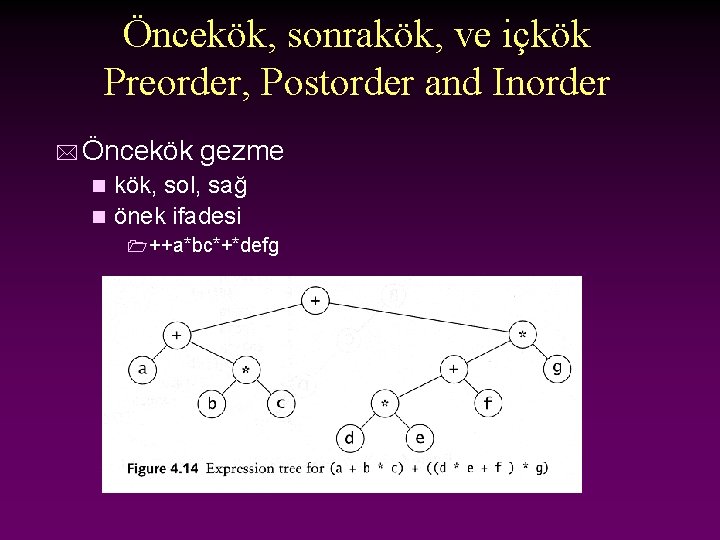
Öncekök, sonrakök, ve içkök Preorder, Postorder and Inorder * Öncekök gezme kök, sol, sağ n önek ifadesi n 1++a*bc*+*defg

Öncekök, sonrakök ve içkök * Sonrakök gezme Sol, sağ, kök n Sonek ifadesi n 1 abc*+de*f+g*+ * İçkök gezme Sol, kök, sağ n İçek ifadesi n 1 a+b*c+d*e+f*g

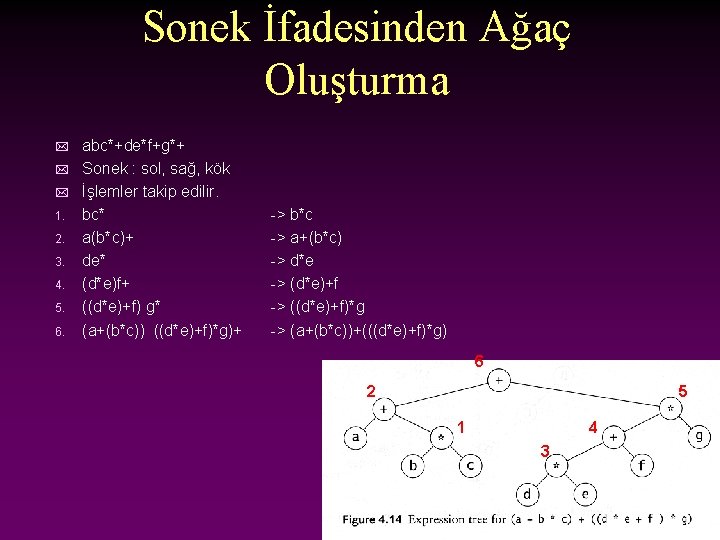
Sonek İfadesinden Ağaç Oluşturma * * * 1. 2. 3. 4. 5. 6. abc*+de*f+g*+ Sonek : sol, sağ, kök İşlemler takip edilir. bc* a(b*c)+ de* (d*e)f+ ((d*e)+f) g* (a+(b*c)) ((d*e)+f)*g)+ -> b*c -> a+(b*c) -> d*e -> (d*e)+f -> ((d*e)+f)*g -> (a+(b*c))+(((d*e)+f)*g) 6 2 5 1 4 3

* Öncekök

* sonrakök

Öncekök, sonrakök ve içkök

İkili Ağaçlar * İkili ağaç SVY üzerindeki muhtemel işlemler parent - ebeveyn n left_child, right_child - sol_çocuk, sağ_çocuk n Sibling - kardeş n root, etc - kök n * Gerçekleştirmesi n İkili ağaçta en fazla iki çocuk olduğu için, bunlar için pointer kullanabiliriz.

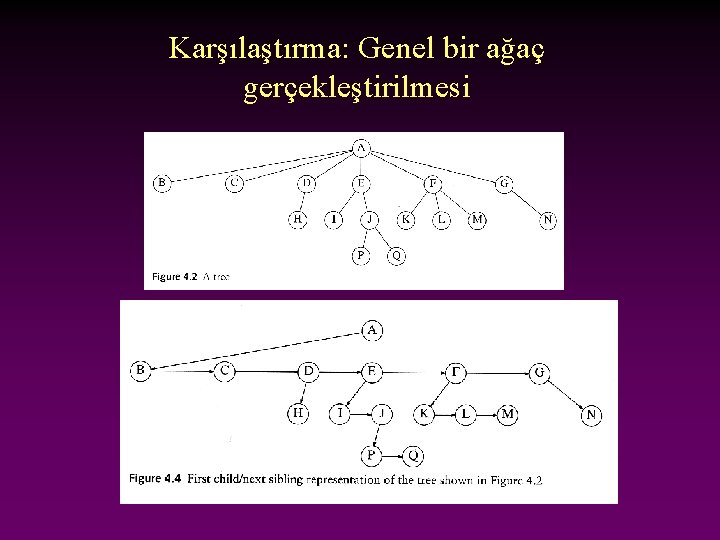
Karşılaştırma: Genel bir ağaç gerçekleştirilmesi

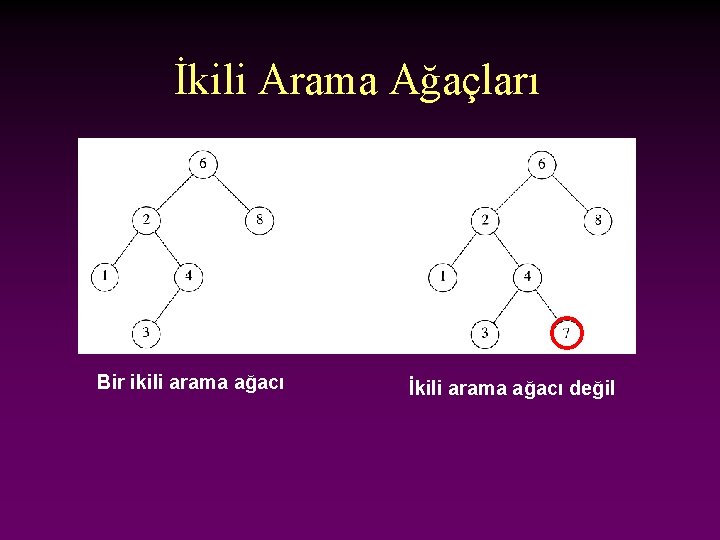
İkili Arama Ağacı * Anahtarları düğümler içinde depolar; böylece arama, ekleme ve silme etkili bir şekilde yapılabilir. İkili arama ağaç özelliği n Herbir X düğümü için, solundaki altağaçtaki (subtree) anahtarlar X düğümünde bulunan değerden daha küçüktür, ve sağındaki ağaçtaki anahtarlar X düğümünde bulunan değerden daha büyüktür.

İkili Arama Ağaçları Bir ikili arama ağacı İkili arama ağacı değil

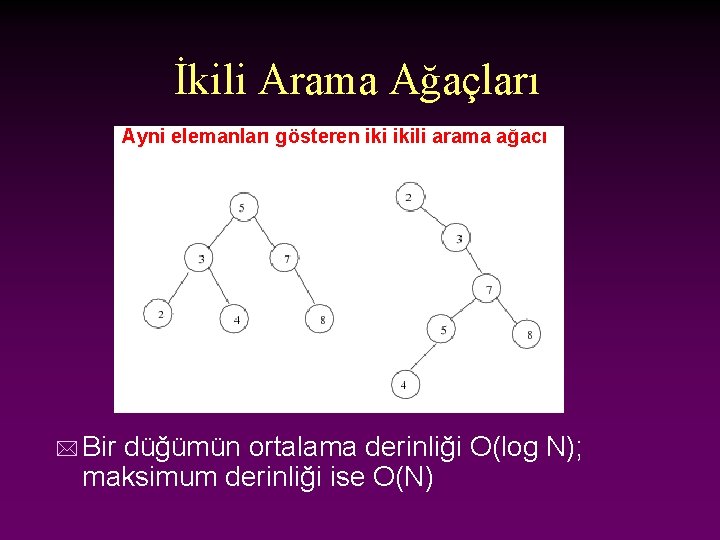
İkili Arama Ağaçları Ayni elemanları gösteren ikili arama ağacı * Bir düğümün ortalama derinliği O(log N); maksimum derinliği ise O(N)

Gerçekleştirme

İAA Arama * Eğer 15’i arıyorsak arama işlemi biter. * Eğer aranan anahtar < 15 ise, sol altağaçta aramaya devam edilir. * Eğer aranan anahtar > 15 ise, sağ altağaçta aramaya devam edilir.

Arama (Bul - Find) * Find X: X anahtarını bulunduran düğümün pointer ini dönder veya eğer böyle bir düğüm yok ise NULL dönder. * Zaman Karmaşıklığı n O(ağaç yüksekliği)

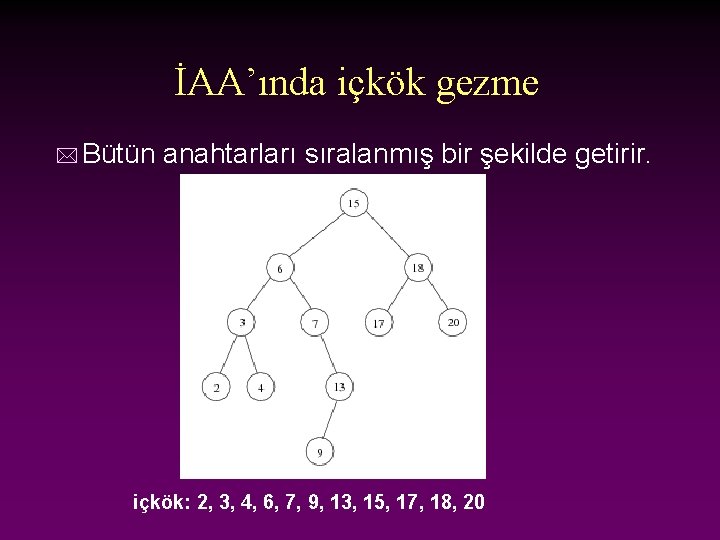
İAA’ında içkök gezme * Bütün anahtarları sıralanmış bir şekilde getirir. içkök: 2, 3, 4, 6, 7, 9, 13, 15, 17, 18, 20

find. Min/ find. Max Ağaçtaki en küçük elemanı içeren düğümü dönderir. * Kökten başla ve sol çocuk var olduğu sürece sola git. Durma noktasındaki eleman en küçük elemandır. * find. Max için de mantık benzer şekildedir. * Zaman karmaşıklığı = O(ağaç yüksekliği) *

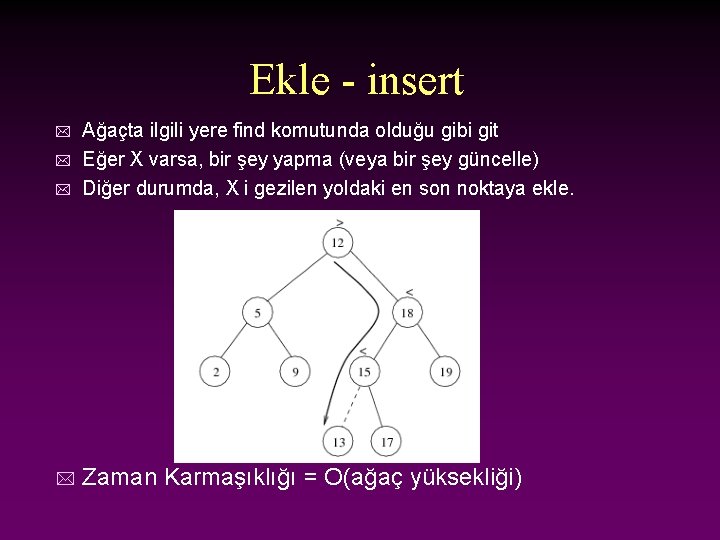
Ekle - insert * Ağaçta ilgili yere find komutunda olduğu gibi git Eğer X varsa, bir şey yapma (veya bir şey güncelle) Diğer durumda, X i gezilen yoldaki en son noktaya ekle. * Zaman Karmaşıklığı = O(ağaç yüksekliği) * *

Sil - delete * Bir düğüm silindiği zaman, silinen düğümün çocuklarına nasıl yerleştireceğimizi düşünmemiş gerekir. n Bu işlem arama ağacı (search tree) özelliğinin korunması için gereklidir.

Sil Üç durum vardır: (1) düğüm yaprak ise n sil (2) düğümün tek çocuğu varsa n Ebeveynden bir çocuğa bir pointer ata

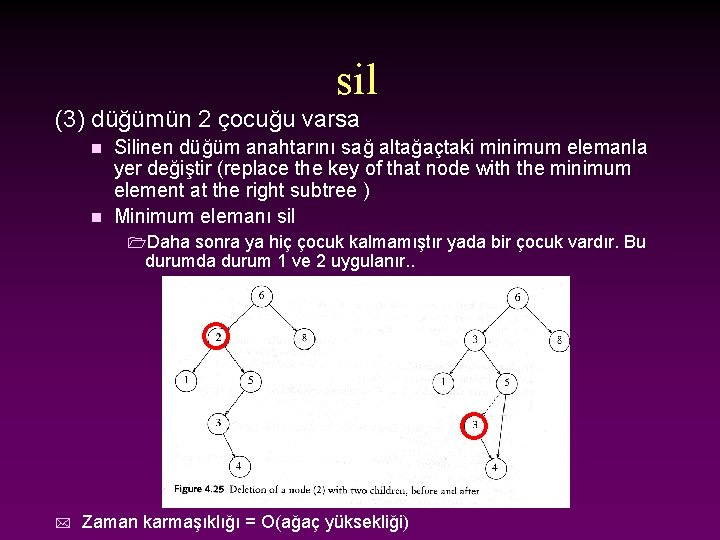
sil (3) düğümün 2 çocuğu varsa Silinen düğüm anahtarını sağ altağaçtaki minimum elemanla yer değiştir (replace the key of that node with the minimum element at the right subtree ) n Minimum elemanı sil n 1 Daha sonra ya hiç çocuk kalmamıştır yada bir çocuk vardır. Bu durumda durum 1 ve 2 uygulanır. . * Zaman karmaşıklığı = O(ağaç yüksekliği)

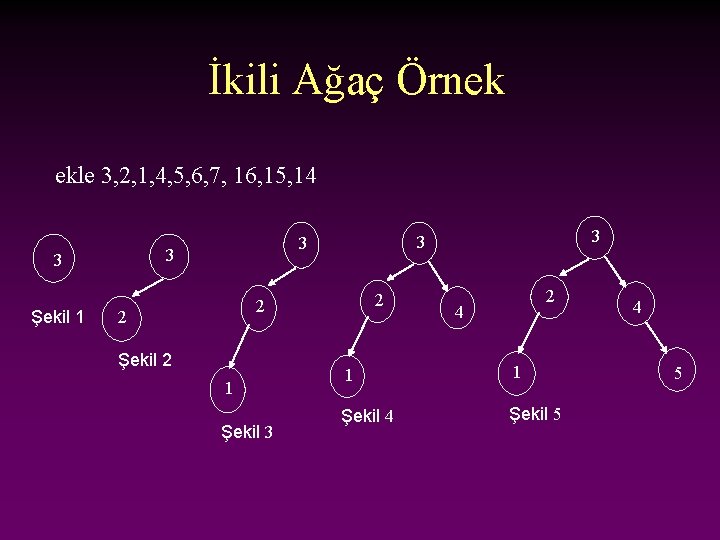
İkili Ağaç Örnek ekle 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 3 Şekil 1 2 2 2 Şekil 2 1 Şekil 3 3 2 4 1 1 Şekil 4 Şekil 5 4 5

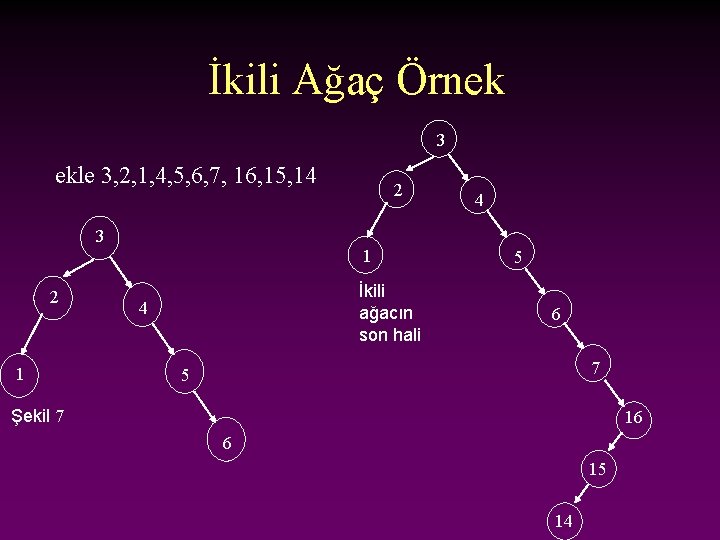
İkili Ağaç Örnek 3 ekle 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 2 1 İkili ağacın son hali 4 4 5 6 7 5 Şekil 7 16 6 15 14

İkili Ağaç Ödev * 18, 5, 15, 3, 12, 9, 6, 8, 4, 13