Key Stage 2 Maths What and how do

Key Stage 2 Maths What and how do we teach it?

Aims of the meeting tonight To help you to understand more of what we do in maths at Key Stage 2 n To enable you to support your child more confidently in maths n To give you more information about what we teach and how we teach maths at Key Stage 2 n

By the end of Key stage 2 we hope that children will…. n n n n n Develop a reliable, accurate method to calculate in all 4 operations Be able to record their working in a compact way Apply basic maths skills to calculations Apply the maths they know to new situations Make links between different areas of maths Develop their own strategies for problem solving, choosing the maths they need to use and how they will record their working. Key stage 2 maths moves from using concrete apparatus to more abstract working and formal recording To do this successfully, children need a firm grasp of basic mental maths skills and the concept of the number system. The key to a good understanding of written methods of calculations is based on mental strategies.

Basic skills in maths n n n Use of the number line and 100 square Counting – forwards, backwards, different steps, decimals Complements Crossing over ‘boundaries’ Multiplication facts and linked division facts Use of money, finding change Time Doubling halving Multiplying and dividing by 10, 1000 Use of calculator Measures – conversion and practical reading of scales

Using number lines “The number line is a powerful and sophisticated linear model of the number system. It embodies all learning styles; visual, auditory and kinaesthetic. It evolves into an internalised mental representation which can be used when children are able to dispense with the actual line. ” Numeracy Team 2002 n

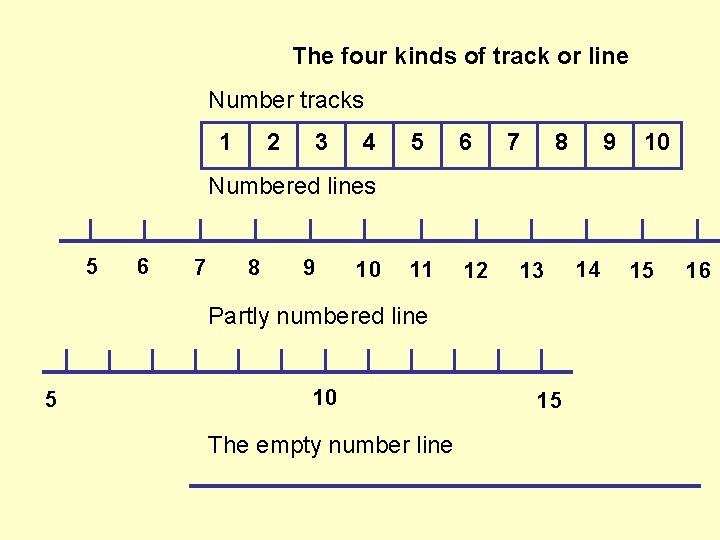
The four kinds of track or line Number tracks 1 2 3 4 5 6 11 12 7 8 9 10 Numbered lines 5 6 7 8 9 10 13 Partly numbered line 5 10 The empty number line 15 14 15 16

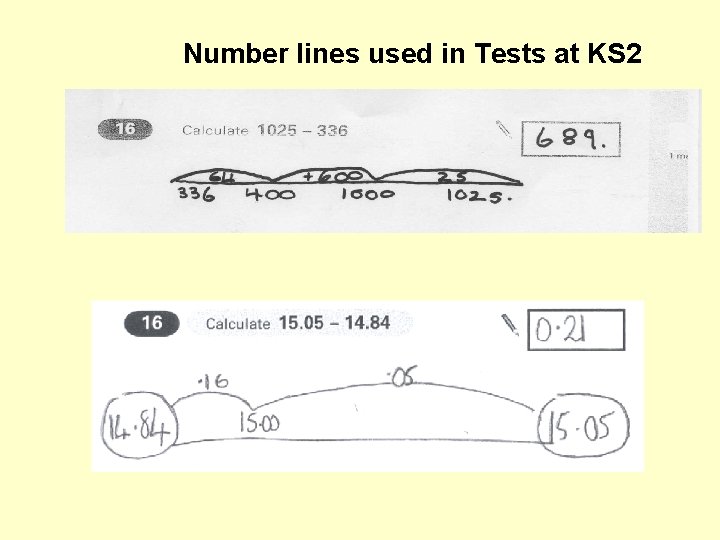
Number lines used in Tests at KS 2

Time lines I started walking at 08: 45 and finished at 12: 25. How long did my walk take me?

Written methods for the 4 operations n n The key to a good understanding of written methods of calculations is based on mental strategies. Each of the four operations builds on mental skills which provide the foundation for jottings and informal written methods of recording. These skills lead on to more formal written methods. The transition between stages depends on a child’s understanding of the method. Not all children will be ready to move on to the next stage at the same time and should not be hurried until they have a secure understanding of the method.

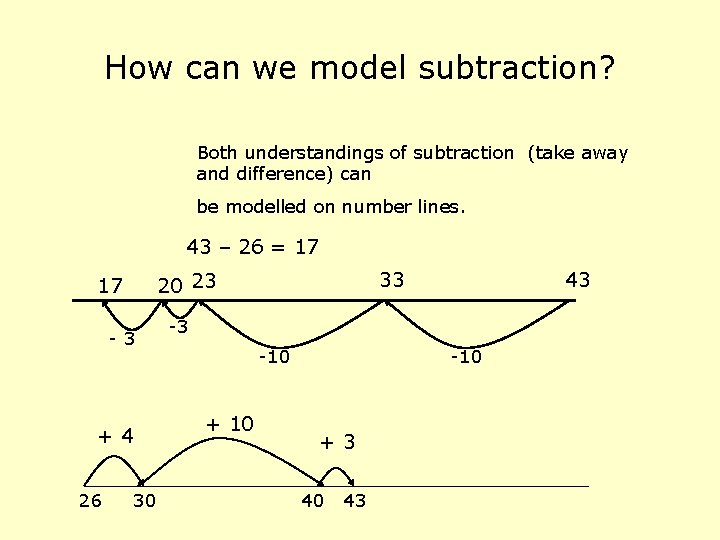
Subtraction 43 – 26 This calculation can be modelled two ways.

How can we model subtraction? Both understandings of subtraction (take away and difference) can be modelled on number lines. 43 – 26 = 17 -3 +4 26 33 20 23 17 30 43 -3 -10 + 10 -10 +3 40 43

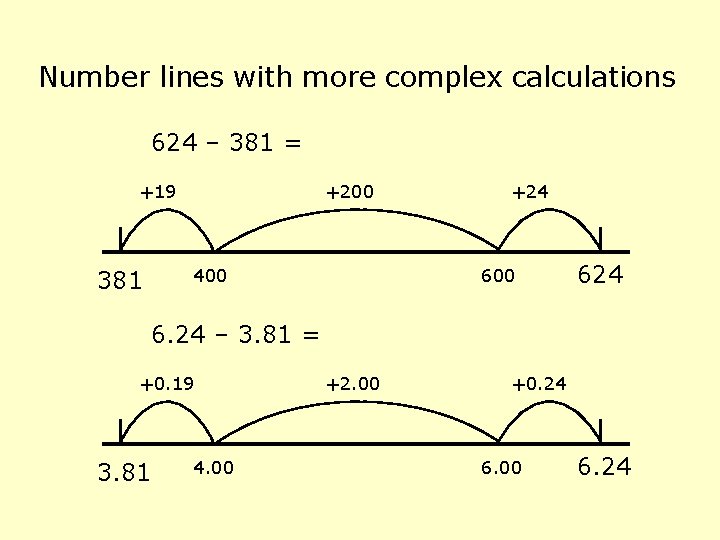
Number lines with more complex calculations 624 – 381 = +19 +200 400 381 +24 600 624 6. 24 – 3. 81 = +0. 19 3. 81 4. 00 +2. 00 +0. 24 6. 00 6. 24

Complementary addition vertically Complementary addition can also be represented vertically. 624 – 381 43 - 26 4 (30) 10 (40) 3 (43) 17 19 (400) 200 (600) 24 (624) 243

Multiplication Arrays are important because they provide a good visual image of the calculation that links closely to the concept of repeated addition. 4 x 2=8 2 x 4=8

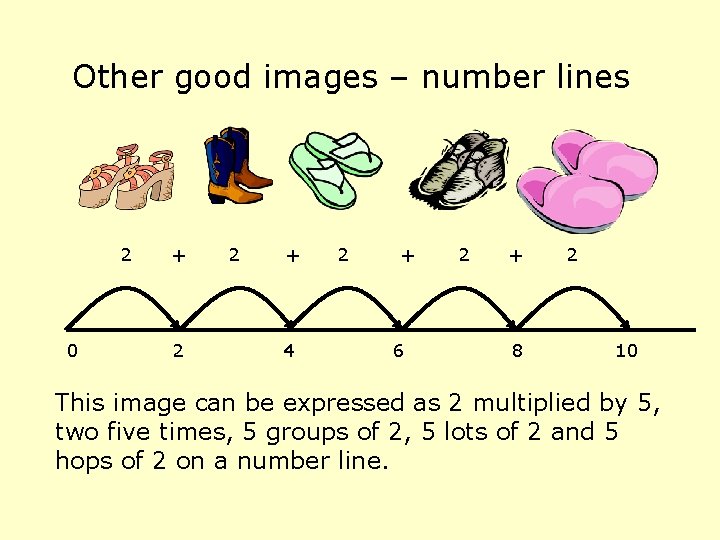
Other good images – number lines 2 0 + 2 2 + 4 2 + 6 2 + 8 2 10 This image can be expressed as 2 multiplied by 5, two five times, 5 groups of 2, 5 lots of 2 and 5 hops of 2 on a number line.

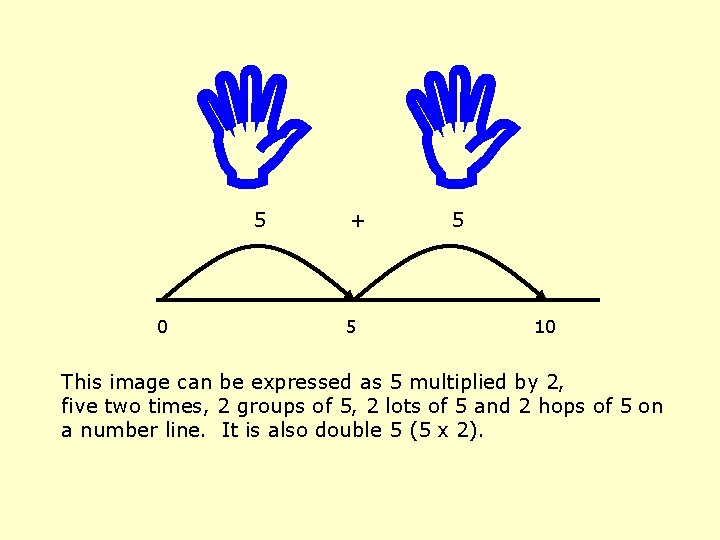
5 0 + 5 5 10 This image can be expressed as 5 multiplied by 2, five two times, 2 groups of 5, 2 lots of 5 and 2 hops of 5 on a number line. It is also double 5 (5 x 2).

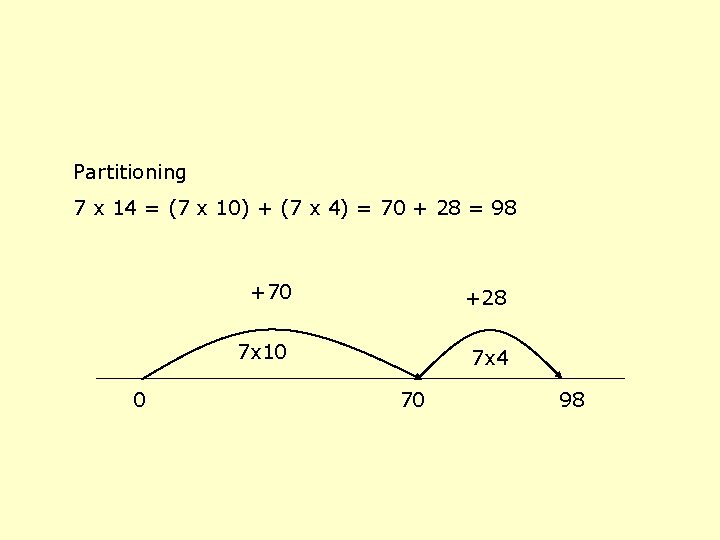
Partitioning 7 x 14 = (7 x 10) + (7 x 4) = 70 + 28 = 98 0 +70 +28 7 x 10 7 x 4 70 98

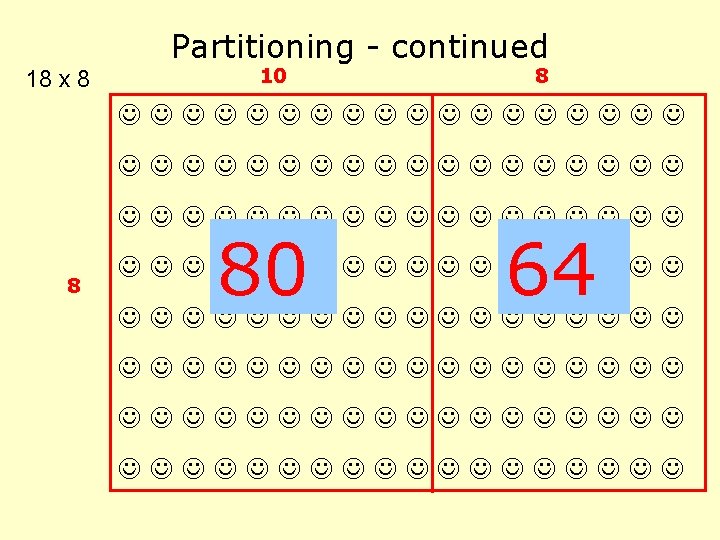
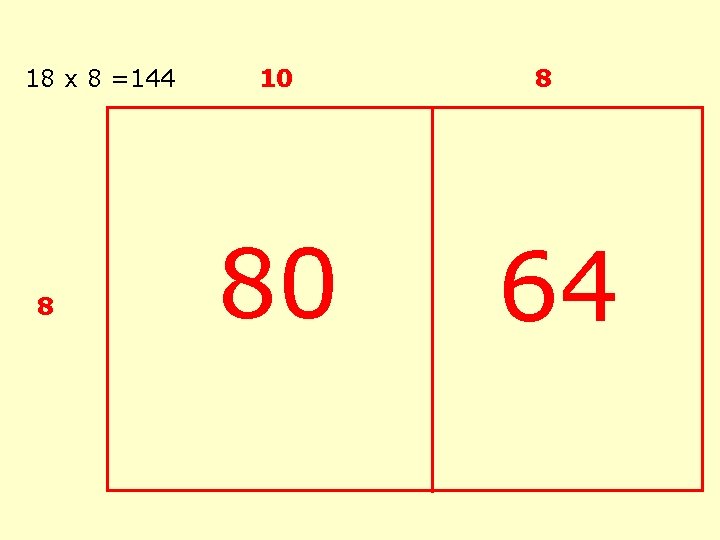
Partitioning - continued 18 x 8 10 8 8 80 64

18 x 8 =144 8 10 80 8 64

Grid method of multiplication 38 x 27 20 30 8 600 160 7 210 810 56 + 216 = + 266 1026

Skills needed to be able to carry out the grid method of multiplication when multiplying 2 twodigit numbers. • partition numbers into tens and units/ones • recall multiplication facts • multiply by ten • multiply by multiples of ten • add together two and three-digit numbers • decide whether the answer is sensible

Multiplying by 10 It is important that multiplying by 10 is not thought of as a case of ‘adding zeros’. It in an inappropriate expression because adding zero actually leaves a number unchanged and the ‘add a zero rule’ fails when, for example, 0. 2 is multiplied by 10 (‘adding a zero’ results in 0. 20). Children need to understand that when you multiply by 10 the digits move one place to the left, leaving an empty space which is filled by zero (a place holder).

Multiplication facts Children will struggle with multiplication if they can’t recall multiplication facts. Knowing a multiplication table is much more than being able to recite it in order. It also means children should be able to respond quickly to oral or written questions phrased in a variety of ways, e. g. • What are six fives? • What is 3 times five? • 5 multiplied by 3 is… • How many fives in 35? • What would I multiply by five to get 30?

Division In Year 3 and 4 children need to know that: • 16 2 does not equal 2 16 • division reverses multiplication (the inverse) – this allows them to solve division calculations by using multiplication strategies (18 3 by counting the hops of 3 to 18) • there will be remainders for some division calculations (to be expressed as wholenumber remainders). • relate division and fractions • use a written method for division (chunking).

Teaching chunking - number line 72 ÷ 5 = Grouping - How many 5’s are there in 72? Adding groups of 5 5 x 10 or 5 x 4 or 10 groups of 5 0 5 10 15 20 25 30 4 groups of 5 35 40 45 50 55 60 65 70 72

Teaching chunking - vertical 5 x 1 =5 5 x 2 = 10 5 x 5 = 25 5 x 10 = 50 72 5 = 72 50 (5 x 10) 22 20 2 Answer: 14 remainder 2 (5 x 4)

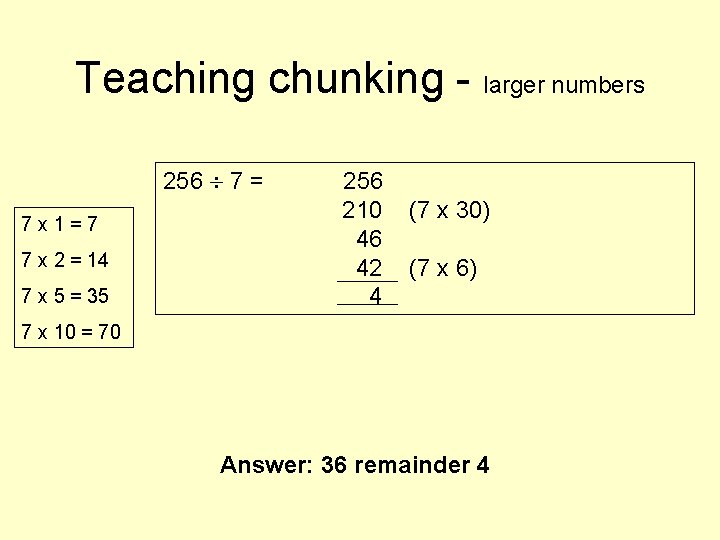
Teaching chunking - larger numbers 256 7 = 7 x 1=7 7 x 2 = 14 7 x 5 = 35 256 210 46 42 4 (7 x 30) (7 x 6) 7 x 10 = 70 Answer: 36 remainder 4

Real Life Problems To make a box pieces of wood 135 mm long have to be cut from a 2. 5 m length. How many lengths of wood can be cut? Train fares cost £ 14. 50. I have £ 52. How many people can I take on the journey?

Teach do we teach maths in school? Abacus Maths scheme n Real life problems n Maths in context – links made with topics n Open ended investigations n Maths during CIL n

How can you help at home? n n Use information on our school website for ideas for support. Refer to the calculation policy on the website Support children with their homework – ask them to explain what they are doing and how Reinforce the basic skills mentioned earlier – these will often be reflected in the targets set by teachers

Any Questions? n Please spend some time looking at the resources around the hall – and have a go at some of the problems!