KETERGANTUNGAN FUNGSIONAL KEY UJI LOSSLES JOIN DECOMPOSITION dekomposisi

KETERGANTUNGAN FUNGSIONAL KEY UJI LOSSLES JOIN DECOMPOSITION

dekomposisi relasi § Dekomposisi : memecah relasi/tabel menjadi relasi/tabel yang lebih kecil untuk mendapatkan skema yang tidak mengandung anomali dan redundansi § Diketahui skema relasi R. Gugus relasi {R 1, R 2, , …, Rn} disebut Dekomposisi dari R jika : R 1 R 2 … Rn = R § Artinya {R 1, R 2, …, Rn} dekomposisi dari R jika setiap atribut dalam R muncul paling sedikit di salah satu Ri untuk 1 i n 2

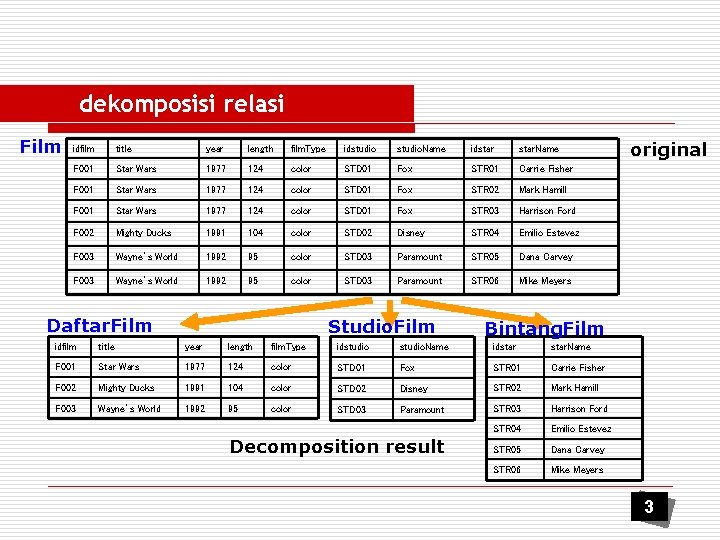
dekomposisi relasi Film idfilm title year length film. Type idstudio. Name idstar. Name F 001 Star Wars 1977 124 color STD 01 Fox STR 01 Carrie Fisher F 001 Star Wars 1977 124 color STD 01 Fox STR 02 Mark Hamill F 001 Star Wars 1977 124 color STD 01 Fox STR 03 Harrison Ford F 002 Mighty Ducks 1991 104 color STD 02 Disney STR 04 Emilio Estevez F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 05 Dana Carvey F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 06 Mike Meyers Daftar. Film Studio. Film Bintang. Film idfilm title year length film. Type idstudio. Name idstar. Name F 001 Star Wars 1977 124 color STD 01 Fox STR 01 Carrie Fisher F 002 Mighty Ducks 1991 104 color STD 02 Disney STR 02 Mark Hamill F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 03 Harrison Ford STR 04 Emilio Estevez STR 05 Dana Carvey STR 06 Mike Meyers Decomposition result original 3

dekomposisi relasi § Dekomposisi relasi R menjadi gugus relasi {R 1, R 2, …, Rn} yang tidak menyebabkan hilangnya informasi disebut Lossless-Join Decomposition. § Dekomposisi relasi R menjadi gugus relasi {R 1, R 2, …, Rn} yang menyebabkan hilangnya informasi disebut Lossy-Join Decomposition. Lossless Join digunakan untuk menjamin keutuhan data untuk operasi gabungan (join) dan merupakan fokus dalam desain basis data relasional 4

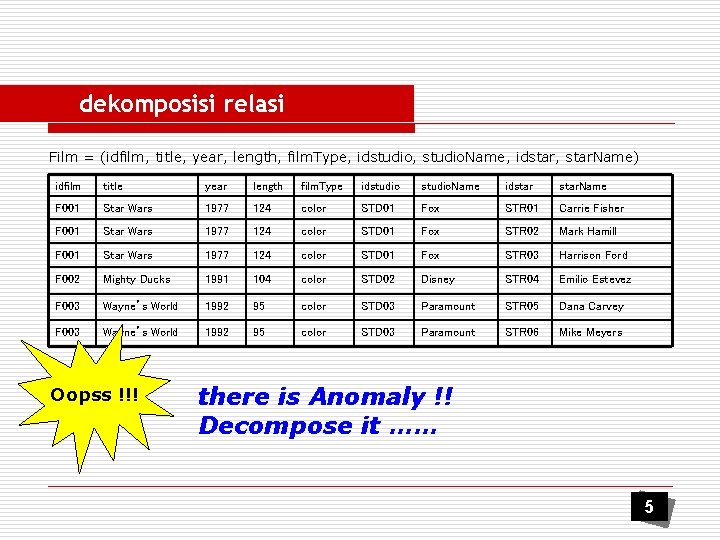
dekomposisi relasi Film = (idfilm, title, year, length, film. Type, idstudio, studio. Name, idstar, star. Name) idfilm title year length film. Type idstudio. Name idstar. Name F 001 Star Wars 1977 124 color STD 01 Fox STR 01 Carrie Fisher F 001 Star Wars 1977 124 color STD 01 Fox STR 02 Mark Hamill F 001 Star Wars 1977 124 color STD 01 Fox STR 03 Harrison Ford F 002 Mighty Ducks 1991 104 color STD 02 Disney STR 04 Emilio Estevez F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 05 Dana Carvey F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 06 Mike Meyers Oopss !!! there is Anomaly !! Decompose it …… 5

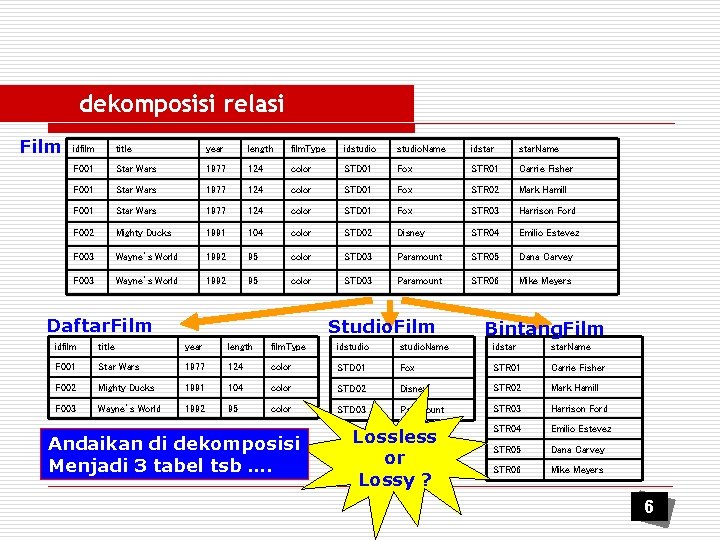
dekomposisi relasi Film idfilm title year length film. Type idstudio. Name idstar. Name F 001 Star Wars 1977 124 color STD 01 Fox STR 01 Carrie Fisher F 001 Star Wars 1977 124 color STD 01 Fox STR 02 Mark Hamill F 001 Star Wars 1977 124 color STD 01 Fox STR 03 Harrison Ford F 002 Mighty Ducks 1991 104 color STD 02 Disney STR 04 Emilio Estevez F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 05 Dana Carvey F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 06 Mike Meyers Daftar. Film Studio. Film Bintang. Film idfilm title year length film. Type idstudio. Name idstar. Name F 001 Star Wars 1977 124 color STD 01 Fox STR 01 Carrie Fisher F 002 Mighty Ducks 1991 104 color STD 02 Disney STR 02 Mark Hamill F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 03 Harrison Ford STR 04 Emilio Estevez STR 05 Dana Carvey STR 06 Mike Meyers Andaikan di dekomposisi Menjadi 3 tabel tsb …. Lossless or Lossy ? 6

dekomposisi relasi Dengan ke-3 tabel hasil dekomposisi, misal ditanyakan informasi : “Di studio manakah Star Wars dibuat ? ” Pasti kita akan membutuhkan tabel Daftar. Film dan Studio. Film. Tapi dapatkah kita diperoleh informasi yang kita inginkan dari kedua skema relasi tersebut ? Tampaknya : TIDAK. Karena kita harus melakukan operasi gabungan terlebih dahulu dari Ke-2 tabel. Misal kita lakukan operasi “cross product” antara Daftar_Film dan Studio. Film. Daftar. Film Studio. Film 7

Kehilangan LOSSY Informasi !! DECOMPOSITION dekomposisi relasi Daftar. Film idfilm title F 001 Studio. Film year length film. Type idstudio. Name Star Wars 1977 124 color STD 01 Fox F 001 Star Wars 1977 124 color STD 02 Disney F 001 Star Wars 1977 124 color STD 03 Paramount F 002 Mighty Ducks 1991 104 color STD 01 Fox F 002 Mighty Ducks 1991 104 color STD 02 Disney F 002 Mighty Ducks 1991 104 color STD 03 Paramount F 003 Wayne’s World 1992 95 color STD 01 Fox F 003 Wayne’s World 1992 95 color STD 02 Disney F 003 Wayne’s World 1992 95 color STD 03 Paramount Ternyata kita tidak mendapatkan informasi yang dibutuhkan, karena film Star Wars dibuat oleh 3 studio (Fox, Disney, Paramount) 8

functional dependencies (FD) § Functional Dependencies (FD) / Ketergantungan Fungsional (KF) digunakan untuk menggambarkan atau mendeskripsikan bentuk normal atas suatu relasi § FD adalah batasan terhadap gugus relasi yang berlaku. Diperoleh berdasarkan hubungan antar atribut data. § Kegunaan FD : 1. Untuk memeriksa keabsahan apakah semua relasi sesuai dengan ketergantungan fungsional yang diberikan 2. Untuk menetapkan batasan gugus relasi yang berlaku 3. Untuk menentukan kunci relasi 4. Untuk melakukan normalisasi atas suatu tabel relasional 9

functional dependencies (FD) definisi Misalkan R adalah suatu skema relasional, atribut x R dan y R maka x dikatakan secara fungsional menentukan y (atau y bergantung secara fungsional pada x), ditulis x y pada R, jika : 1. Semua tupel ti [x], 1 i n adalah unik/tunggal 2. Semua pasangan tupel dimana ti [x] = tj [x], i j, terjadi juga ti [y] = tj [y] dengan kata lain : Untuk setiap nilai x terdapat hanya satu nilai y (x menentukan secara tunggal nilai y). Jadi apabila terdapat 2 tuple t 1 dan t 2 mempunyai nilai atribut x yang sama, maka juga akan mempunyai nilai atribut y yang sama. t 1[x] = t 2 [x] t 1[y] = t 2 [y] pada skema relasi R 10

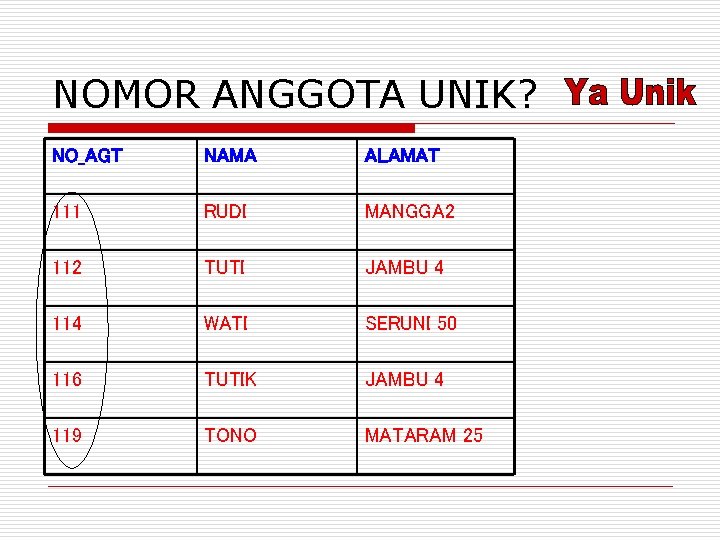
NOMOR ANGGOTA UNIK? NO_AGT NAMA ALAMAT 111 RUDI MANGGA 2 112 TUTI JAMBU 4 114 WATI SERUNI 50 116 TUTIK JAMBU 4 119 TONO MATARAM 25

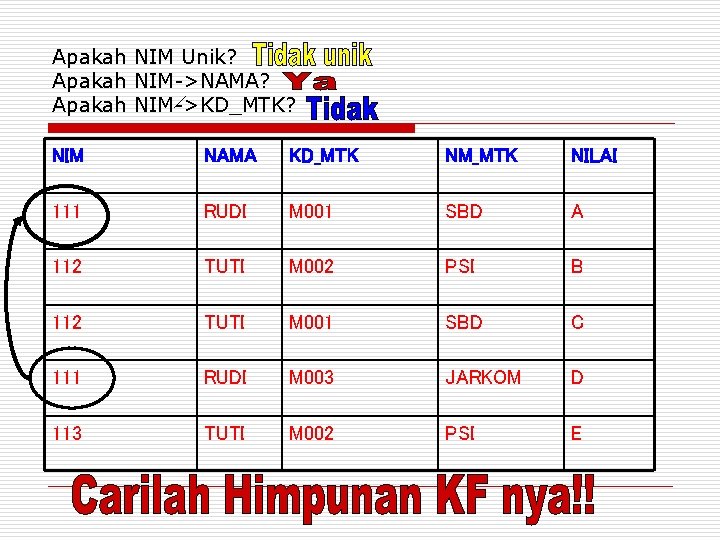
Apakah NIM Unik? Apakah NIM->NAMA? Apakah NIM->KD_MTK? NIM NAMA KD_MTK NM_MTK NILAI 111 RUDI M 001 SBD A 112 TUTI M 002 PSI B 112 TUTI M 001 SBD C 111 RUDI M 003 JARKOM D 113 TUTI M 002 PSI E

HIMPUNAN KF o NIM-> NAMA o KD_MTK -> NM_MTK o NIM, KD_MTK -> NILAI

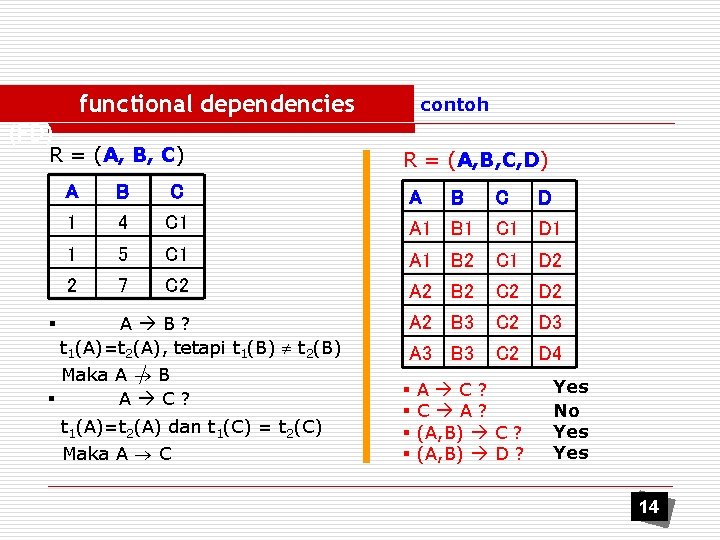
functional dependencies contoh (FD) R = (A, B, C) § R = (A, B, C, D) A B C A 1 4 C 1 A 1 B 1 C 1 D 1 1 5 C 1 A 1 B 2 C 1 D 2 2 7 C 2 A 2 B 2 C 2 D 2 A 2 B 3 C 2 D 3 A 3 B 3 C 2 D 4 A B? t 1(A)=t 2(A), tetapi t 1(B) t 2(B) Maka A B § A C? t 1(A)=t 2(A) dan t 1(C) = t 2(C) Maka A C § § B C A C? C A? (A, B) C ? (A, B) D ? D Yes No Yes 14

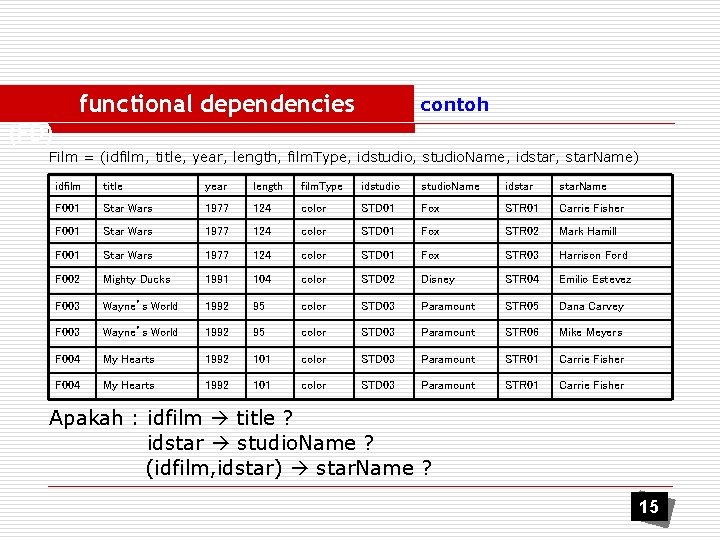
functional dependencies contoh (FD) Film = (idfilm, title, year, length, film. Type, idstudio, studio. Name, idstar, star. Name) idfilm title year length film. Type idstudio. Name idstar. Name F 001 Star Wars 1977 124 color STD 01 Fox STR 01 Carrie Fisher F 001 Star Wars 1977 124 color STD 01 Fox STR 02 Mark Hamill F 001 Star Wars 1977 124 color STD 01 Fox STR 03 Harrison Ford F 002 Mighty Ducks 1991 104 color STD 02 Disney STR 04 Emilio Estevez F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 05 Dana Carvey F 003 Wayne’s World 1992 95 color STD 03 Paramount STR 06 Mike Meyers F 004 My Hearts 1992 101 color STD 03 Paramount STR 01 Carrie Fisher Apakah : idfilm title ? idstar studio. Name ? (idfilm, idstar) star. Name ? 15

functional dependencies (FD) § FD dirumuskan berdasarkan batasan dari dunia nyata suatu atribut. Contoh : - Nomor Induk mahasiswa menentukan Nama. Mahasiswa NIM Nama. Mhs - Kode Matakuliah menentukan Nama Mata Kuliah dan SKS Kode. MK (Nama. MK, SKS) - NIM dan Kode Mata Kuliah menentukan Nilai Matakuliah (NIM, Kode. MK) Nilai. MK 16

FD TRIVIAL § Suatu FD : x y disebut trivial jika y x Contoh : X X X, Y Y X, Y, Z X, Z X, Y, Z 17

Armstrong’s Rule Diketahui A 1. Reflexive Dari A 2 Jika y x maka x y Diketahui A 2. Augmentation Dari A 3 Jika x y maka (x, z) (y, z) A 3. Transitive Jika x y dan y z maka x z A 4. Decomposition Jika x (y, z) maka x y dan x z A 5. Union Jika x y dan x z maka x (y, z) A 6. Pseudotranstivity Jika x y dan (z, y) w maka (x, z) w x y (x, z) (y, z) (z, y) w (x, z) w 18

Manfaat FD pada dekomposisi Untuk : 1. Lossless Join Decomposition Mendapatkan dekomposisi yang tidak kehilangan data/informasi 2. No Redundancy Mendapatkkan skema relasi yang tidak mengandung redundansi 3. Dependency Preservation Terjaminnya pemeliharaan ketergantungan sehingga dapat mengatasi masalah update anomali 19

uji lossless-join decomposition Misal diketahui skema relasi R didekomposisi menjadi gugus relasi {R 1, R 2, R 3, R 4, …, Rn}, maka dekomposisi ini disebut Lossless Join Decomposition jika kondisi R 1 R 2 R 3 … Rn Ri dipenuhi sekurang-kurangnya untuk 1 nilai i, dimana 1 i n. Dengan kata lain, jika diketahui skema relasi R didekomposisi menjadi gugus relasi {R 1, R 2}, maka dekomposisi ini disebut Lossless Join Decomposition jika dipenuhi salah satu kondisi : § R 1 R 2 R 1 atau § R 1 R 2 Langkah-2 Uji Lossless-joint Decomposition : 1. Uji Dekomposisi R 1 R 2 … Rn = R 2. Uji Lossless-join Menggunakan sifat ketergantungan fungsional 20

uji lossless-join decomposition contoh Diketahui skema relasi R=(A, B, C, D, E, F, G, H) didekomposisi menjadi : R 1=(A, B, C, D, G) dan R 2=(B, D, E, F, H). FD pada R yang berlaku adalah : (1) B A, G (2) E D, H (3) A E, C (4) D F Ujilah apakah dekomposisi {R 1, R 2} tersebut lossless atau lossy ? 1. Uji Dekomposisi R 1 R 2 = (A, B, C, D, G) (B, D, E, F, H) = (A, B, C, D, E, F, G, H) =R. : . Terbukti bahwa {R 1, R 2} adalah dekomposisi dari R. 21

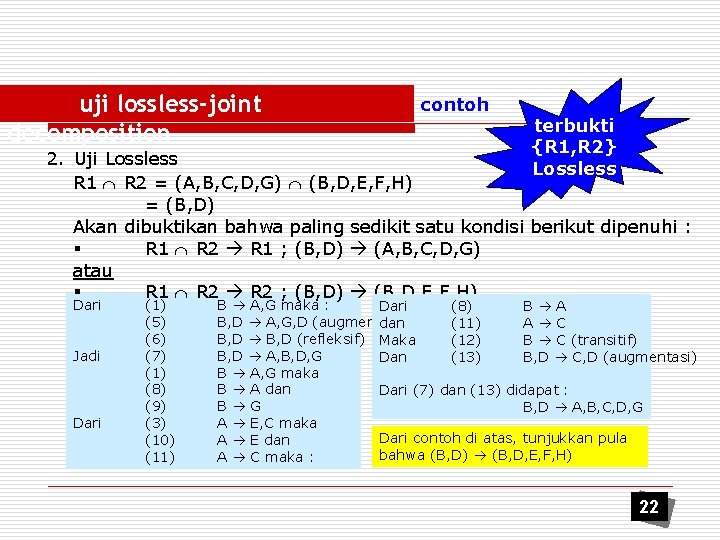
uji lossless-joint decomposition contoh terbukti {R 1, R 2} Lossless 2. Uji Lossless R 1 R 2 = (A, B, C, D, G) (B, D, E, F, H) = (B, D) Akan dibuktikan bahwa paling sedikit satu kondisi berikut dipenuhi : § R 1 R 2 R 1 ; (B, D) (A, B, C, D, G) atau § R 1 R 2 ; (B, D) (B, D, E, F, H) Dari Jadi Dari (1) (5) (6) (7) (1) (8) (9) (3) (10) (11) B A, G maka : Dari (8) B A B, D A, G, D (augmentasi) dan (11) A C B, D (refleksif) Maka (12) B C (transitif) B, D A, B, D, G Dan (13) B, D C, D (augmentasi) B A, G maka B A dan Dari (7) dan (13) didapat : B G B, D A, B, C, D, G A E, C maka Dari contoh di atas, tunjukkan pula A E dan bahwa (B, D) (B, D, E, F, H) A C maka : 22

functional dependencies Closure FD (F+) (FD) § Misal F adalah gugus ketergantungan fungsional pada skema relasi R, maka semua FD yang mungkin dapat diturunkan dari F dengan hukum -hukum FD disebut : Closure dari F, ditulis F+. § Armstrong’s rule dapat dimanfaatkan untuk menentukan F + Contoh : Diketahui R = (A, B, C, D) F = { A B, B C, A C, C D} maka : § A D sebab A C dan C D, dari sifat transitif (A 3) didapat A D § B D sebab B C dan C D, dari sifat transitif (A 3) didapat B D Sehingga {A B, B C, A C, C D, A D, B D} F+. Kita dapat menurunkan anggota-anggota F+ yang lain berdasarkan FD yang diketahui menggunakan Armstong’s rule. Closure FD (F+) berguna untuk Uji Dependency Preservation 23

uji dependency preservation Misal skema relasi R dengan himpunan ketergantungan fungsional F didekomposisi menjadi R 1, R 2, R 3, …, Rn. Dan F 1, F 2, F 3, …, Fn adalah himpunan ketergantungan fungsional yang berlaku di R 1, R 2, R 3, …, Rn maka dekomposisi tersebut dikatakan memenuhi sifat Dependency Preservation apabila berlaku : (F 1 F 2 F 3 … Fn)+ = F+ Dependency Preservation (Pemeliharaan Ketergantungan) merupakan kriteria yang menjamin keutuhan relasi ketika suatu relasi didekomposisi menjadi beberapa tabel. Sehingga diharapkan tidak terjadi inkonsistensi atau anomali ketika dilakukan update data. 24

uji dependency preservation Contoh : Diketahui skema relasi R=(A, B, C) dengan FD : A B ; B C Didekomposisi menjadi R 1=(A, B) dan R 2=(B, C) a. Apakah dekomposisi tsb Lossless-Joint ? b. Apakah dekomposisi tsb memenuhi Dependency Preservation ? a. R 1 R 2 = (A, B) (B, C) = (A, B, C) = R R 1 R 2 = (A, B) (B, C) = B Lossless jika B (A, B) atau B (B, C). Karena diketahui B C maka BB BC atau B BC (Augmentasi). Jadi dekomposisi tsb Lossless. 25

uji dependency preservation b. closure R=(A, B, C) dan F = {A B, B C}. Karena A B dan B C maka A C. Maka dapat dibentuk F+={A B, B C, A C}. R 1=(A, B) dan F 1={A B}. Karena hanya A B yang berlaku di R 1. R 2=(B, C) dan F 2={B C}. Karena hanya B C yang berlaku di R 2. § § F 1 F 2 = {A B, B C}. Karena A B dan B C maka A C. Sehingga (F 1 F 2 )+={A B, B C, A C}=F+ Ujilah dekomposisinya apakah Lossless dan Dependency Preservat Apabila R di atas didekoposisi menjadi R 1=(A, B) dan R 2=(A, C). Jadi dekomposisi tsb memenuhi Dependency Preservation. Bagaimana bila R 1=(A, B) dan R 2=(B, C) tetapi FD : B C, AC B 26

soal latihan Ujilah dekomposisi dari skema relasi R, apakah lossless atau lossy ? 1. R = (A, B, C, D, E, F, G, H) didekomposisi menjadi : R 1 = (A, B, C, D, E) dan R 2 = (C, D, F, G, H) dengan FD : C (A, B, D) ; F (G, H) ; D (E, F) 2. R = (A, B, C, D, E) didekomposisi menjadi : R 1 = (A, B, C, D) dan R 2 = (C, D, E) dengan FD : A B ; (C, D) E ; B D ; E A 3. R = (X, Y, Z, W, U, V) didekomposisi menjadi : R 1 = (X, Y, Z, W) dan R 2 = (W, U, V) dengan FD : W X; X Z 4. R = (A, B, C, D, E, F) didekomposisi menjadi : R 1 = (A, B, C), R 2 = (A, D, F) dan R 3 = (E, D) dengan FD : A (B, C) ; D (F, A) Ujilah pula dependency preservation nya untuk masing-masing soal tsb. 27

KEYS 28

atribut kunci (key) § § § Kunci (key) adalah kolom/atribut atau kombinasi kolom/atribut yang dapat digunakan untuk mengidentifikasi baris dalam tabel (entitas) secara unik. Penentuan Key suatu tabel didasarkan pada sifat “determinasi”. Determinan : gugus atribut dimana satu atau lebih atribut lain tergantung secara fungsional. “A determinan B” artinya apabila nilai atribut A akan menentukan nilai-nilai atribut B. “A determinan B” dapat dituliskan sebagai suatu ketergantungan fungsional A B. Jika A menentukan B, C dan D maka dituliskan A B, C, D. Contoh : Relasi Mahasiswa=(NIM, Nama, Agama, Tgl. Lhr) Bila nilai NIM seorang mahasiswa diketahui maka dapat digunakan untuk melihat nilai-nilai atribut Nama, Agama dan Tanggal Lahirnya. Dituliskan NIM Nama, Agama, Tgl. Lhr 29

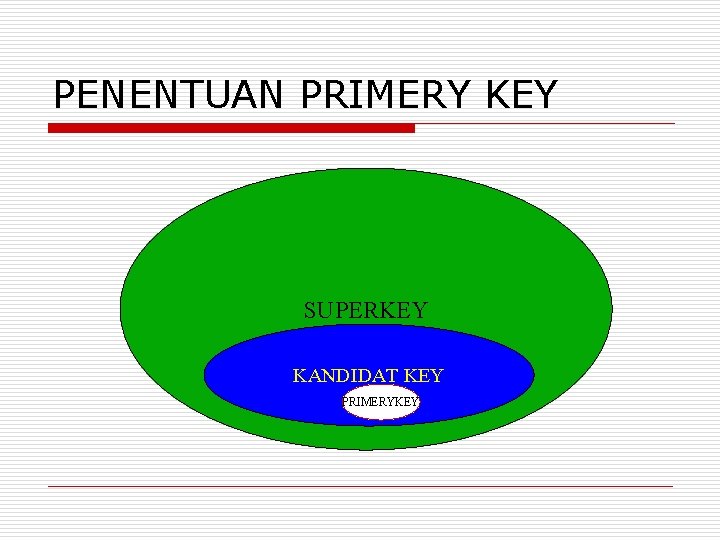
superkey Superkey (key) : gugus atribut entitas yang dapat digunakan untuk mengidentifikasikan entitas/obyek secara unik. satu atau lebih atribut yang membedakan setiap baris secara unik. Misal R skema relasi, dan K adalah satu atau lebih atribut dari R dimana K R maka K disebut Superkey jika dan hanya jika K R. Catatan : Suatu skema relasi dapat memiliki lebih dari 1 superkey. Bila K adalah superkey maka semua atribut gabungan yang mengandung K juga merupakan superkey Contoh : Relasi Sopir=(No. KTP, No. SIM, Nama, Alamat). Alternatif superkey : § No. KTP superkey ; No. KTP Sopir § No. SIM superkey ; No. SIM Sopir § (No. KTP, No. SIM) superkey ; (No. KTP, No. SIM) Sopir § (No. KTP, Nama) superkey ; (No. KTP, Nama) Sopir § (No. KTP, No. SIM, Nama) superkey ; (No. SKTP, No. SIM, Nama) Sopir § (No. KTP, No. SIM, Nama, Alamat) dengan sendirinya juga superkey § Nama bukan superkey. Demikian juga (Nama, Alamat) juga bukan superkey 30

candidate key § Candidate Key : - Superkey dengan jumlah atribut minimal - Superkey tanpa redundansi (tidak memuat subset superkey yang lain) K adalah Candidate Key dari skema relasi R jika dan hanya jika : K R dan tidak terdapat K dengan R Contoh : Skema relasi Sopir=(No. KTP, No. SIM, Nama, Alamat). Alternatif superkey : § No. KTP superkey ; No. KTP Sopir § No. SIM superkey ; No. SIM Sopir § (No. KTP, No. SIM) superkey ; (No. KTP, No. SIM) Sopir § (No. KTP, Nama) superkey ; (No. KTP, Nama) Sopir § (No. KTP, No. SIM, Nama) superkey ; (No. SKTP, No. SIM, Nama) Sopir § (No. KTP, No. SIM, Nama, Alamat) dengan sendirinya juga superkey Sebagai Candidate Key nya adalah No. KTP atau No. SIM 31

primary key Primary Key adalah candidate key yang dipilih untuk digunakan sebagai kunci identitas tabel secara unik (kunci indeks tabel) dan tidak boleh bernilai NULL. Dasar pemilihan Candidate Key sebagai Primary Key : § Key tsb menjamin keunikan baris data § Key tsb bersifat natural atau universal (lazim dipakai sebagai acuan) § Key tsb mudah dan ringkas untuk dipakai sebagai acuan § Contoh : Skema relasi Sopir=(No. KTP, No. SIM, Nama, Alamat). Alternatif superkey : § No. KTP superkey ; No. KTP Sopir § No. SIM superkey ; No. SIM Sopir § (No. KTP, No. SIM) superkey ; (No. KTP, No. SIM) Sopir § (No. KTP, Nama) superkey ; (No. KTP, Nama) Sopir § (No. KTP, No. SIM, Nama) superkey ; (No. SKTP, No. SIM, Nama) Sopir § (No. KTP, No. SIM, Nama, Alamat) dengan sendirinya juga superkey Sebagai Candidate Key nya adalah No. KTP atau No. SIM Maka No. SIM lebih baik dipilih sebagai Primary Key untuk skema relasi Sopir 32

secondary key § § Secondary Key adalah atribut (atau kombinasinya), yang digunakan sebagai perantara untuk mendapatkan kembali data asal. Biasanya dipakai pada pencarian data (data retrieval). Contoh : Skema relasi Sopir=(No. KTP, No. SIM, Nama, Alamat) dengan No. SIM sebagai Primary Key. Walaupun atribut ini lazim dipakai sebagai identitas seorang Sopir, tapi apakah seorang sopir dijamin hapal nomor SIM nya ketika misalnya ada transaksi yang berkaitan dengan penggunaan identitas No SIM ? . Untuk memudahkan proses pencarian data sopir tersebut maka dapat digunakan atribut lain yang lebih mudah diingat misalnya “nama” dan/atau “alamat”. Penggunaan secondary key ini tentu saja tidak menjamin ditemukannya data uang unik, karena memang tidak ditujukan untuk kepentingan keunikan data. Tetapi sebagai alternatif atau fasilitas untuk membantu mengidentifikasi data. Analogikan ketika kita lupa akan ID atau password account email kita. Fasilitas apa yang bisa kita manfaatkan ? 33

PENENTUAN PRIMERY KEY SUPERKEY KANDIDAT KEY PRIMERYKEY

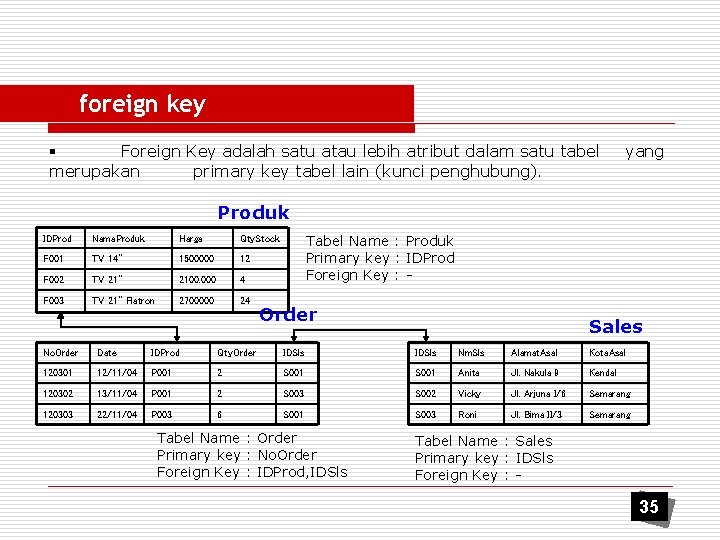
foreign key § Foreign Key adalah satu atau lebih atribut dalam satu tabel merupakan primary key tabel lain (kunci penghubung). yang Produk IDProd Nama. Produk Harga Qty. Stock F 001 TV 14” 1500000 12 F 002 TV 21” 2100. 000 4 F 003 TV 21” Flatron 2700000 24 Tabel Name : Produk Primary key : IDProd Foreign Key : - Order Sales No. Order Date IDProd Qty. Order IDSls Nm. Sls Alamat. Asal Kota. Asal 120301 12/11/04 P 001 2 S 001 Anita Jl. Nakula 9 Kendal 120302 13/11/04 P 001 2 S 003 S 002 Vicky Jl. Arjuna I/6 Semarang 120303 22/11/04 P 003 6 S 001 S 003 Roni Jl. Bima II/3 Semarang Tabel Name : Order Primary key : No. Order Foreign Key : IDProd, IDSls Tabel Name : Sales Primary key : IDSls Foreign Key : - 35

HUBUNGAN ANTARA SUPERKEY DENGAN KETERGANTUNGAN FUNGSIONAL Definisi: R adalah skema relasi , K disebut superkey dari R jika K R, dimana K R. Contoh: R{NIM, NAMA, ALAMAT} NIM adalah superkey karena NIM R NIM, NAMA adalah superkey karena NIM, NAMA R NAMA adalah bukan superkey karena NAMA R

hubungan FD dengan key Amstrong’s rule dapat digunakan untuk menurunkan superkey tabel, berdasarkan 1 atau lebih superkey yang diketahui Rule 1 : Apabila diketahui FD yang memuat semua atribut pada tabel, maka atribut-atribut yang terdapat pada ruas kiri dari FD adalah superkey Contoh : Diketahui tabel R = (W, X, Y, Z) dan FD : XY WZ maka XY superkey Sebab : XY WZ maka XY (refleksif) XY XYWZ (union) XY R Karena XY R maka XY superkey. Jadi ruas kiri dari FD merupakan superkey. 37

hubungan FD dengan key Rule 2 : Atribut yang secara fungsional menentukan superkey dari tabel maka atribut tersebut juga merupakan superkey Contoh : Diketahui W superkey dari tabel R = (W, X, Y, Z) dan FD : Z W maka Z superkey Sebab : Z W dan W WXYZ (karena W superkey), maka Z WXYZ (transitif) Z R Karena Z R maka Z superkey 38

hubungan FD dengan key R = (A, B, C, D) A B C D A 1 B 1 C 1 D 1 A 1 B 2 C 1 D 2 A 2 B 2 C 2 D 2 A 2 B 3 C 2 D 3 A 3 B 3 C 2 D 4 § Apakah (A, B) superkey dari R ? Akan dibuktikan apakah (A, B) R. Jika Ya maka (A, B) superkey dari R. Karena semua tupel ti[A, B] untuk 1 i 5 adalah unik, t 1[A, B]=(A 1, B 1) t 2[A, B]=(A 1, B 2) t 3[A, B]=(A 2, B 2) t 4[A, B]=(A 2, B 3) t 5[A, B]=(A 3, B 3) Maka (A, B) (A, B, C, D) atau (A, B) R Jadi (A, B) superkey dari R § Apakah A superkey dari R ? Bukan, sebab A R. Mengapa ? 39

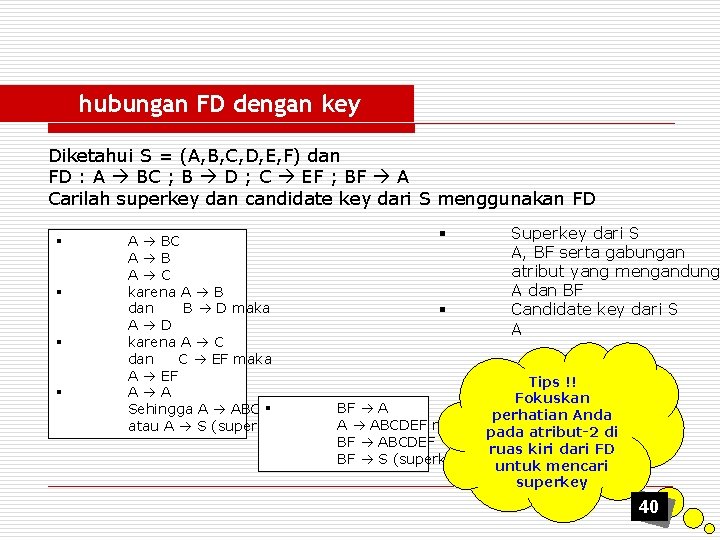
hubungan FD dengan key Diketahui S = (A, B, C, D, E, F) dan FD : A BC ; B D ; C EF ; BF A Carilah superkey dan candidate key dari S menggunakan FD § § A BC A B A C karena A B dan B D maka A D karena A C dan C EF maka A EF A A § Sehingga A ABCDEF atau A S (superkey) § § BF A A ABCDEF maka BF ABCDEF BF S (superkey) Superkey dari S A, BF serta gabungan atribut yang mengandung A dan BF Candidate key dari S A Tips !! Fokuskan perhatian Anda pada atribut-2 di ruas kiri dari FD untuk mencari superkey 40

hubungan FD dengan key Latihan : 1. Diberikan R(A, B, C, D) dengan FD : A B, A C dan A D Apakah A candidate key dari R ? 2. Diberikan R(A, B, C, D) dengan FD : A B a. Apakah ACD superkey dari R b. Apakah A candidate key dari R 3. Diberikan R(A, B, C, D, E, F) dengan FD : C (AB); B (DE); E F; A BC a. Carilah superkey dari R b. Carilah candidate key dari R 4. Diberikan R(A, B, C, D, E) dengan FD : A (BC); (CD) E; B D; E A a. Carilah superkey dari R b. Carilah candidate key dari R 5. Diberikan R(A, B, C) dengan FD : A B; B C; C A Apakah A merupakan satu-satunya candidate key dari R 41

End Session Today Tomorrow We’ll Discuss About Normalization …… 42