Kerr festival Kerr Festival 2004 Christchurch 2004 Reflection


















- Slides: 27

Kerr festival Kerr Festival 2004 Christchurch 2004

Reflection from horizon of black holes Michael Kuchiev School of Physics, UNSW Kerr Festival 2004 Christchurch

Plan: • Reflection on the horizon • Escape effect from under the horizon, information extraction • Conclusion RH and EE do exist Kerr Festival 2004 Christchurch

Black holes Impossible What is lost indeed (Что упало то пропало ) (Except for Hawking effect) And here Escape is Perfect prison possible ! What happens here ? Reflection ! Kerr Festival 2004 Christchurch

Schwarzschild black hole: Kerr Festival 2004 Christchurch

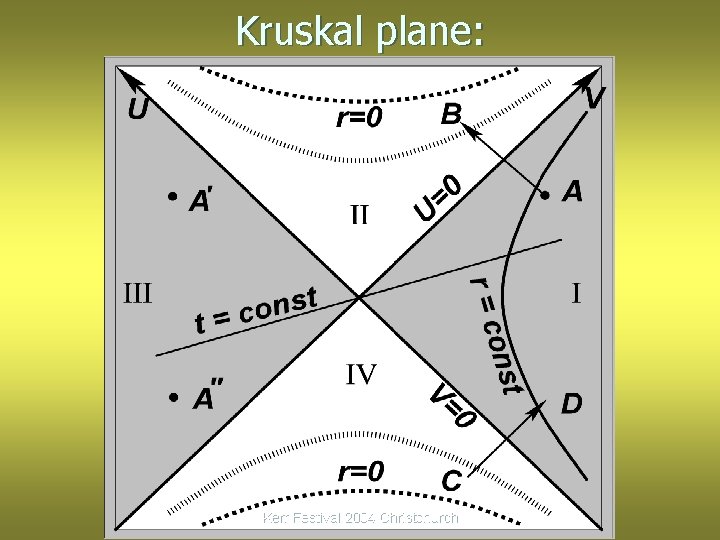
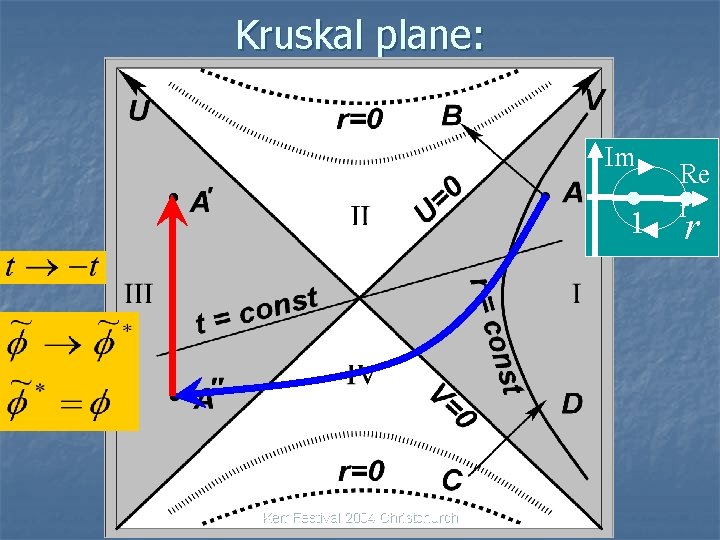
Kruskal plane: Kerr Festival 2004 Christchurch

Hawking radiation: The event horizon of a (Schwarzschild) black hole has a finite temperature Kerr Festival 2004 Christchurch

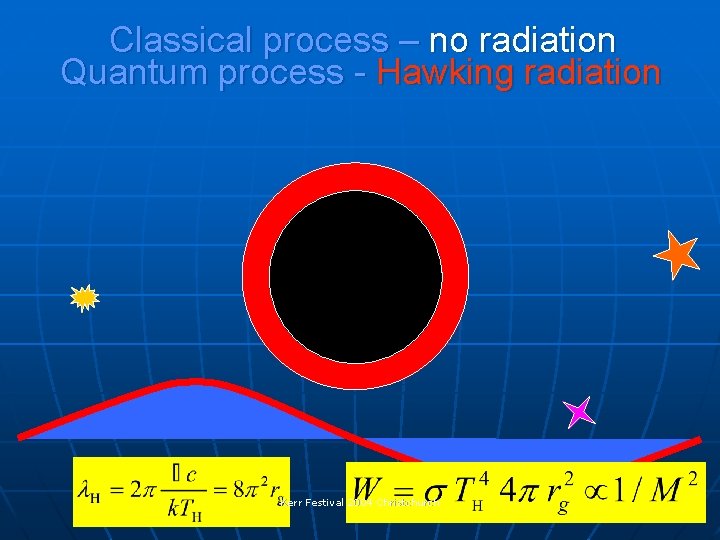
Classical process – no radiation Quantum process - Hawking radiation Kerr Festival 2004 Christchurch

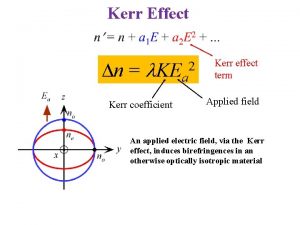
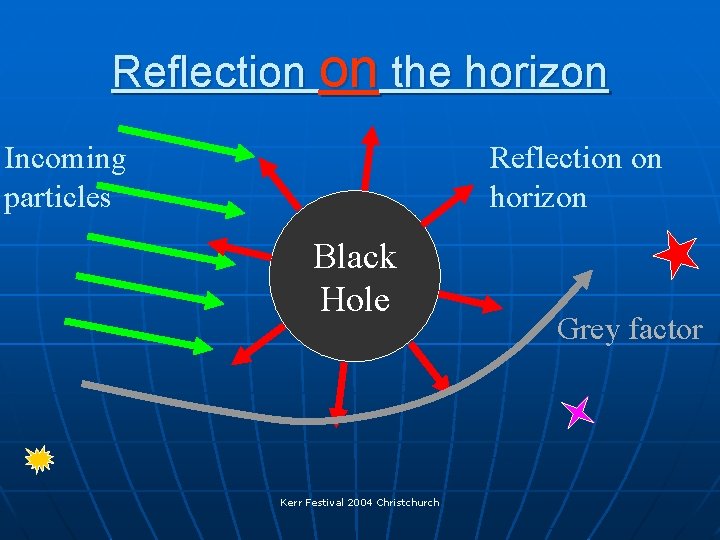
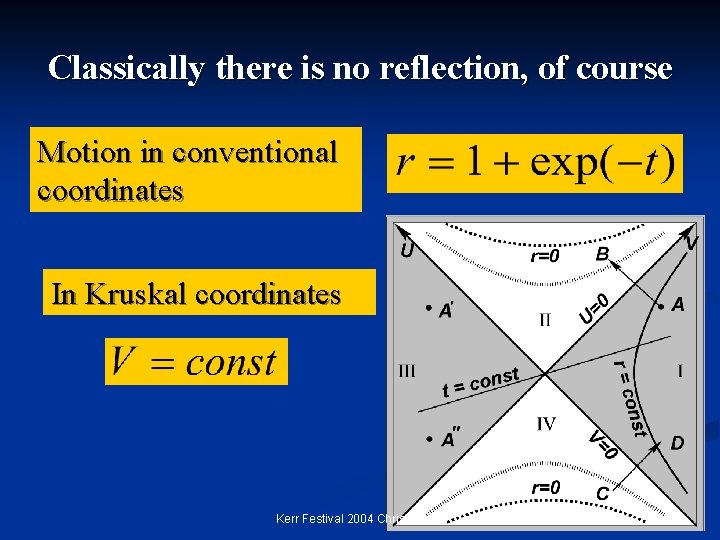
New effect – reflection on horizon • Classically there is no reflection on the horizon. • Conventionally this fact is taken as a proof that the incoming particle inevitably goes inside a black hole (and stays thereafter). • Quantum treatment reveals that there is a probability for the incoming particle to bounce from the horizon back, into the outside world. Kerr Festival 2004 Christchurch

Reflection on the horizon Incoming particles Reflection on horizon Black Hole Kerr Festival 2004 Christchurch Grey factor

Consider Schwarzschild black hole: Kerr Festival 2004 Christchurch

Klein-Gordon equation for scalar massless particle, s- wave Kerr Festival 2004 Christchurch

Boundary condition on the horizon: Here R is the reflection coefficient. • R=0 is the conventional assumption. • |R|>0 means that there is the reflection. Question: HOW to find R ? Kerr Festival 2004 Christchurch

Classically there is no reflection, of course Motion in conventional coordinates In Kruskal coordinates Kerr Festival 2004 Christchurch

How to verify that |R>0 ? Idea: use analytical properties of the wave function. Im r Consider complex plane r Re r 1 r Kerr Festival 2004 Christchurch

Analytical continuation gives: Im 1 This is fundamentally important, verified below Kerr Festival 2004 Christchurch Re r r

Miracle: there is the reflection on the horizon ! Probability of reflection on the horizon: Kerr Festival 2004 Christchurch

For Kerr black holes When black holes behave as reflectors ! Kerr Festival 2004 Christchurch

Kruskal plane: Im 1 Kerr Festival 2004 Christchurch Re r r

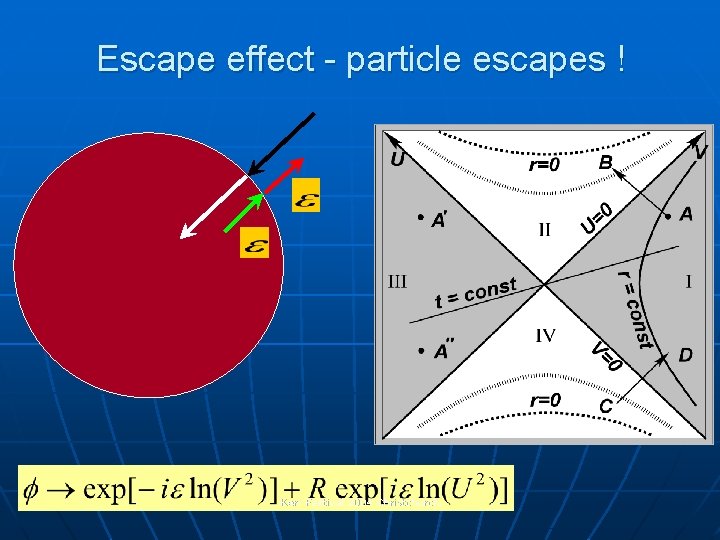
Escape effect - particle escapes ! Kerr Festival 2004 Christchurch

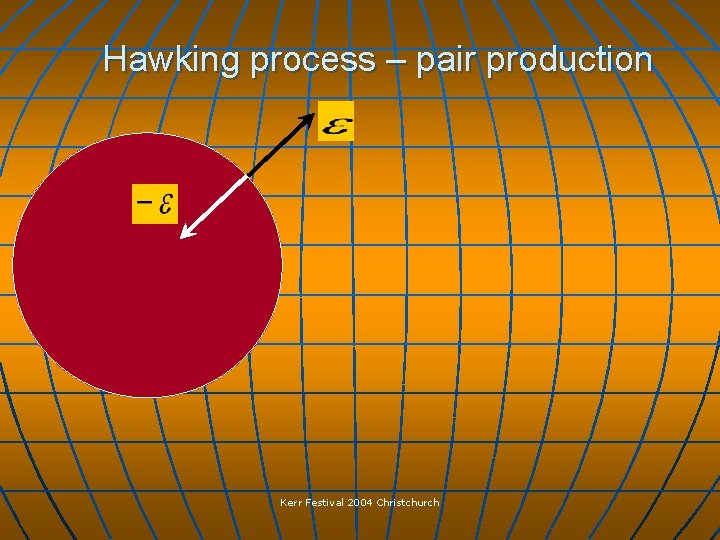
Hawking process – pair production Kerr Festival 2004 Christchurch

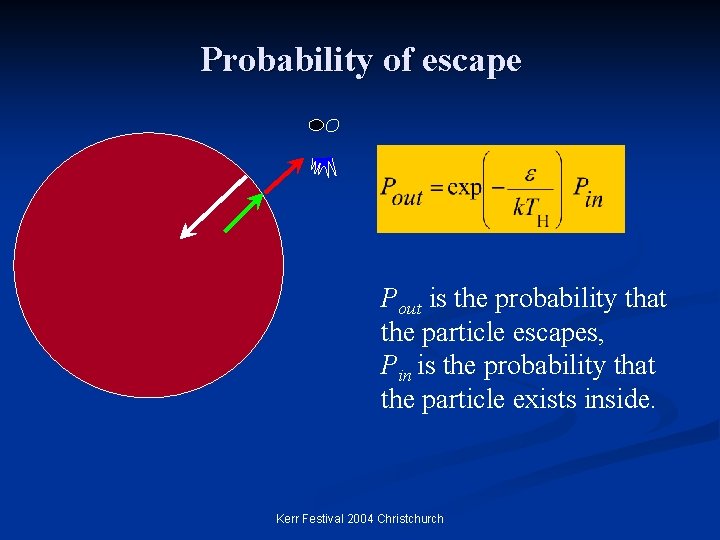
Probability of escape Pout is the probability that the particle escapes, Pin is the probability that the particle exists inside. Kerr Festival 2004 Christchurch

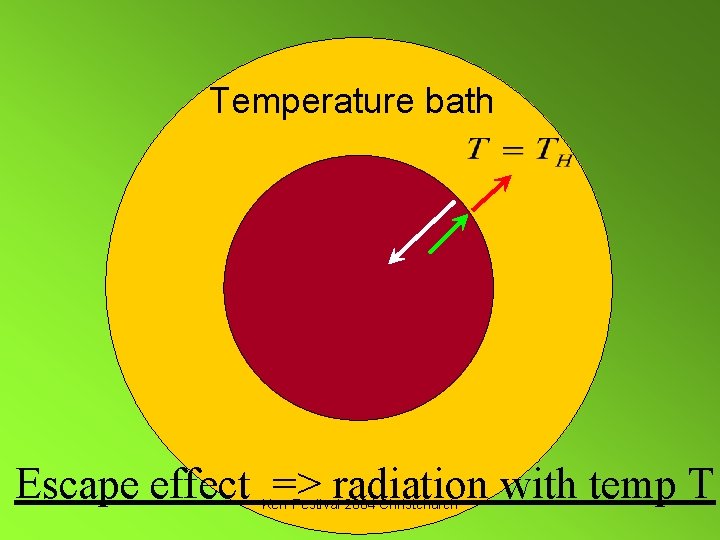
Temperature bath Escape effect => radiation with temp T Kerr Festival 2004 Christchurch

No bath Radiation due to escape effect still exists. However, the information goes out ! Kerr Festival 2004 Christchurch

Conclusions: • • The horizon reflects particles A particle can escape The information can be retrieved from under the horizon A number of fundamental issues related to black holes are to be affected: • • Black holes at early stages of the universe Primordial black holes – interaction with matter Entropy of black holes Etc, there is a long way to go Kerr Festival 2004 Christchurch

Acknowledgments l. Roy Kerr, thank you for the solution and the birthday party l. Some results presented were obtained in collaboration with Victor Flambaum. l. Support of the Australian Research Council is acknowledged. l. Resources and slides from Internet were used. l. Kerr Patience of the listeners is much Festival 2004 Christchurch

References: • • • M. Yu. Kuchiev, Europhys. Lett. 65, 445 (2004). M. Yu. Kuchiev, Phys. Rev. D 69, 124031 (2004). M. Yu. Kuchiev, gr-qc/0310008. M. Yu. Kuchiev and V. V. Flambaum, Scattering of scalar particles by black holes, Phys. Rev. D 69, 124031 (2004) M. Yu. Kuchiev and V. V. Flambaum, Phys. Rev D 70, 044022 (2004) M. Yu. Kuchiev, V. V. Flambaum, gr-qc/0407077 Kerr Festival 2004 Christchurch
 Marijane meaker
Marijane meaker Steve kerr madeleine kerr
Steve kerr madeleine kerr Christchurch bay sediment cell
Christchurch bay sediment cell Backflow christchurch
Backflow christchurch Meniscus lens ray diagram
Meniscus lens ray diagram Mappa di kerr cos'è
Mappa di kerr cos'è K flexofile
K flexofile Trapano traduzione
Trapano traduzione Ruth groff
Ruth groff Histerotomia tipo beck
Histerotomia tipo beck Mappa di kerr castoldi
Mappa di kerr castoldi Ripe database download
Ripe database download Mappa di kerr
Mappa di kerr Kerr lake regional water system
Kerr lake regional water system Mappa di kerr
Mappa di kerr Muller munro kerr
Muller munro kerr Repertorio orm
Repertorio orm Peter truong
Peter truong Dr ashley kerr
Dr ashley kerr Model leiningerové
Model leiningerové Kerr environmental services
Kerr environmental services Kerr modulator
Kerr modulator Hashcat wpa
Hashcat wpa Kerr vs kronig incision
Kerr vs kronig incision Charmaine kerr
Charmaine kerr Gary kerr omaha
Gary kerr omaha Metaparadigma leininger
Metaparadigma leininger Turbo intake manifold design
Turbo intake manifold design