Kernelized Value Function Approximation for Reinforcement Learning Gavin

Kernelized Value Function Approximation for Reinforcement Learning Gavin Taylor and Ronald Parr Duke University

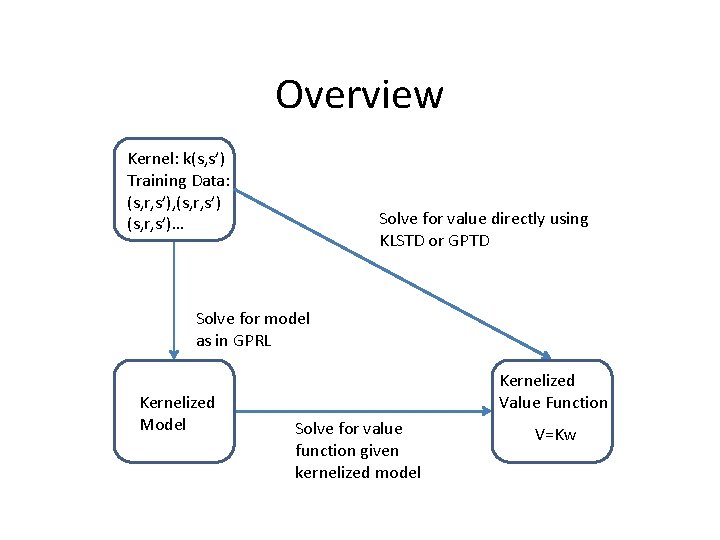
Overview Kernel: k(s, s’) Training Data: (s, r, s’), (s, r, s’)… Solve for value directly using KLSTD or GPTD Solve for model as in GPRL Kernelized Model Kernelized Value Function Solve for value function given kernelized model V=Kw

Overview - Contributions • Construct new model-based VFA • Equate novel VFA with previous work • Decompose Bellman Error into reward and transition error • Use decomposition to understand VFA Samples Model VFA Bellman Error reward error transition error

Outline • Motivation, Notation, and Framework • Kernel-Based Models – Model-Based VFA – Interpretation of Previous Work • Bellman Error Decomposition • Experimental Results and Conclusions

Markov Reward Processes • M=(S, P, R, ) • Value: V(s)=expected, discounted sum of rewards from state s • Bellman equation: • Bellman equation in matrix notation:

Kernels • Properties: – Symmetric function between two points: – PSD K-matrix • Uses: – Dot-product in high-dimensional space (kernel trick) – Gain expressiveness • Risks: – Overfitting – High computational cost

Outline • Motivation, Notation, and Framework • Kernel-Based Models – Model-Based VFA – Interpretation of Previous Work • Bellman Error Decomposition • Experimental Results and Conclusions

Kernelized Regression • Apply kernel trick to least-squares regression • t: target values • K: kernel matrix, where • k(x): column vector, where • : regularization matrix

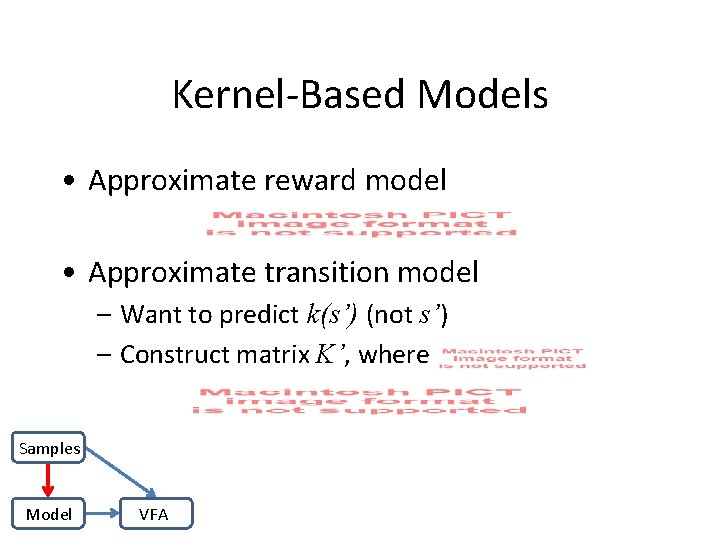
Kernel-Based Models • Approximate reward model • Approximate transition model – Want to predict k(s’) (not s’) – Construct matrix K’, where Samples Model VFA

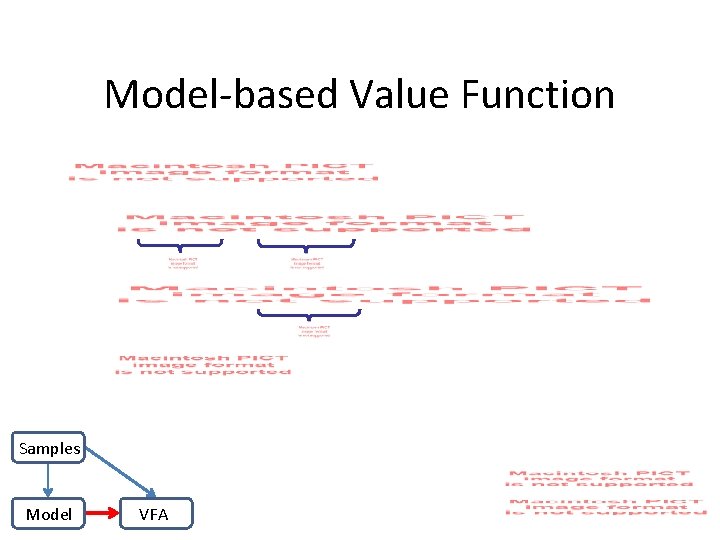
Model-based Value Function Samples Model VFA

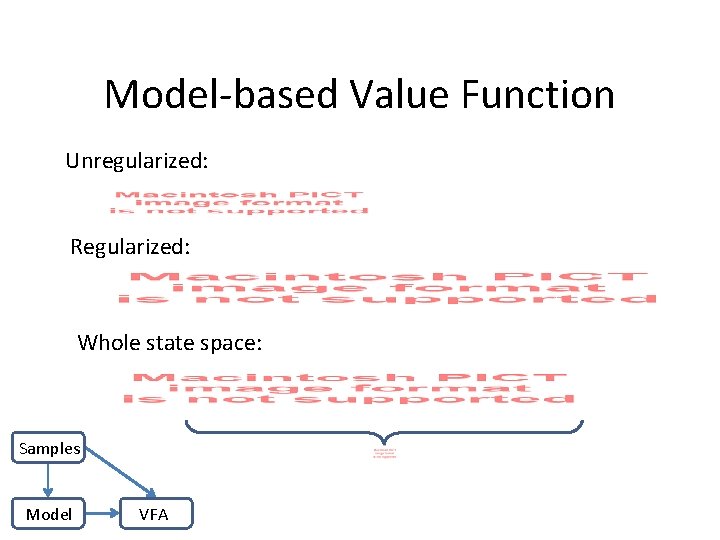
Model-based Value Function Unregularized: Regularized: Whole state space: Samples Model VFA

Previous Work • Kernel Least-Squares Temporal Difference Learning (KLSTD) [Xu et. al. , 2005] – Rederive LSTD, replacing dot products with kernels – No regularization • Gaussian Process Temporal Difference Learning (GPTD) [Engel, et al. , 2005] – Model value directly with a GP • Gaussian Processes in Reinforcement Learning (GPRL) [Rasmussen and Kuss, 2004] Samples Model – Model transitions and value with GPs – Deterministic reward VFA

Equivalency Method Value Function Model-based Equivalent KLSTD GPRL Modelbased [T&P `09] Samples : GPTD noise parameter Model VFA : GPRL regularization parameter

Outline • Motivation, Notation, and Framework • Kernel-Based Models – Model-Based VFA – Interpretation of Previous Work • Bellman Error Decomposition • Experimental Results and Conclusions

Model Error • Error in reward approximation: • Error in transition approximation: : expected next kernel values : approximate next kernel values

Bellman Error a linear combination of reward and transition errors reward error transition error

Outline • Motivation, Notation, and Framework • Kernel-Based Models – Model-Based VFA – Interpretation of Previous Work • Bellman Error Decomposition • Experimental Results and Conclusions

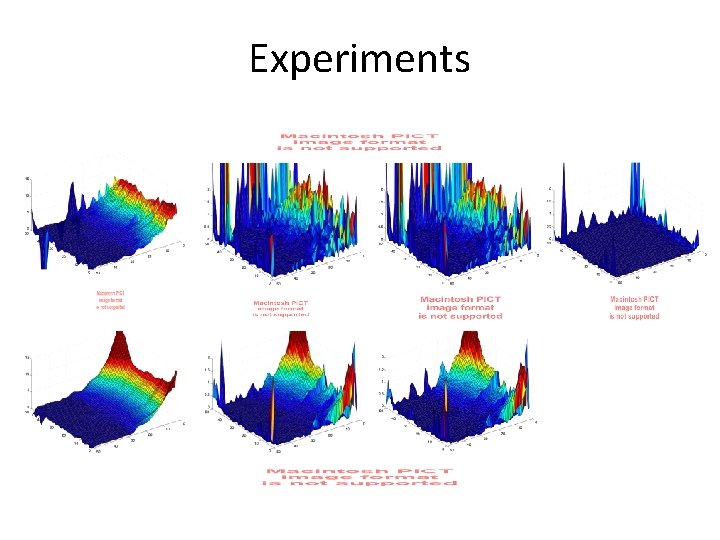
Experiments • Version of two room problem [Mahadevan & Maggioni, 2006] • Use Bellman Error decomposition to tune regularization parameters REWARD

Experiments

Conclusion • Novel, model-based view of kernelized RL built around kernel regression • Previous work differs from model-based view only in approach to regularization • Bellman Error can be decomposed into transition and reward error • Transition and reward error can be used to tune parameters

Thank you!

What about policy improvement? • Wrap policy iteration around kernelized VFA – Example: KLSPI – Bellman error decomposition will be policy dependent – Choice of regularization parameters may be policy dependent • Our results do not apply to SARSA variants of kernelized RL, e. g. , GPSARSA

What’s left? • Kernel selection – Kernel selection (not just parameter tuning) – Varying kernel parameters across states – Combining kernels (See Kolter & Ng ‘ 09) • Computation costs in large problems – K is O(#samples) – Inverting K is expensive – Role of sparsification, interaction w/regularization

Comparing model-based approaches • Transition model – GPRL: models s’ as a GP – T&P: approximates k(s’) given k(s) • Reward model – GPRL: deterministic reward – T&P: reward approximated with regularized, kernelized regression

Don’t you have to know the model? • For our experiments & graphs: Reward, transition errors calculated with true R, K’ • In practice: Cross-validation could be used to tune parameters to minimize reward and transition errors

Why is the GPTD regularization term asymmetric? • GPTD is equivalent to T&P when • Can be viewed as propagating the regularizer through the transition model – – Is this a good idea? – Our contribution: Tools to evaluate this question

What about Variances? • Variances can play an important role in Bayesian interpretations of kernelized RL – Can guide exploration – Can ground regularization parameters • Our analysis focuses on the mean • Variances a valid topic for future work

Does this apply to the recent work of Farahmand et al. ? • Not directly • All methods assume (s, r, s’) data • Farahmand et al. include next states (s’’) in their kernel, i. e. , k(s’’, s) and k(s’’, s’) • Previous work, and ours, includes only s’ in the kernel: k(s’, s)

How is This Different from Parr et al. ICML 2008? • Parr et al. considers linear fixed point solutions, not kernelized methods • Equivalence between linear fixed point methods was fairly well understood already • Our contribution: – We provide a unifying view of previous kernel-based methods – We extend the equivalence between model-based and direct methods to the kernelized case