Kernel adaptive filtering Lecture slides for EEL 6502

Kernel adaptive filtering Lecture slides for EEL 6502 Spring 2011 Sohan Seth

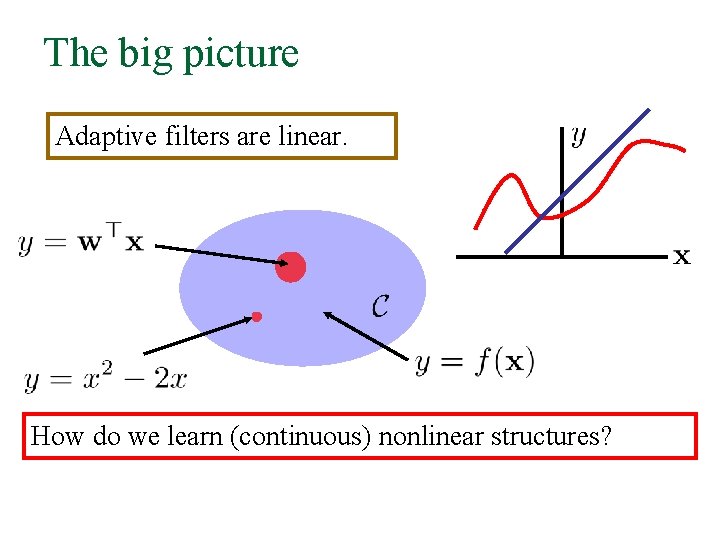
The big picture Adaptive filters are linear. How do we learn (continuous) nonlinear structures?

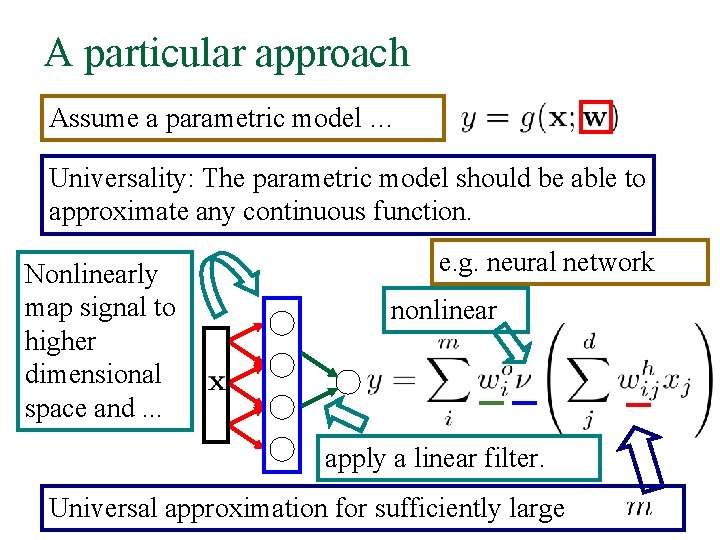
A particular approach Assume a parametric model … Universality: The parametric model should be able to approximate any continuous function. Nonlinearly map signal to higher dimensional space and. . . e. g. neural network nonlinear apply a linear filter. Universal approximation for sufficiently large

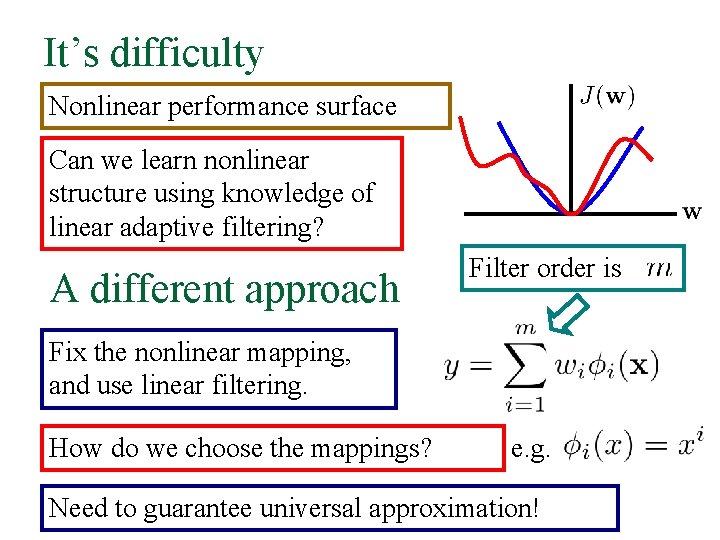
It’s difficulty Nonlinear performance surface Can we learn nonlinear structure using knowledge of linear adaptive filtering? A different approach Filter order is Fix the nonlinear mapping, and use linear filtering. How do we choose the mappings? e. g. Need to guarantee universal approximation!

A ‘trick’y solution Top-down design Optimal filter exists in the span of input data *** Output is a projection e. g Mapping is infinite dimensional. Only the inner product matters, not the mapping

Inner product and pd kernel are equivalent Inner product space: Linear space with inner product 1. Symmetry, Positive definite (pd) kernel 2. Linearity, e. g. or, 3. Positive definiteness is an inner product in some space Use pd kernel to implicitly construct nonlinear mapping

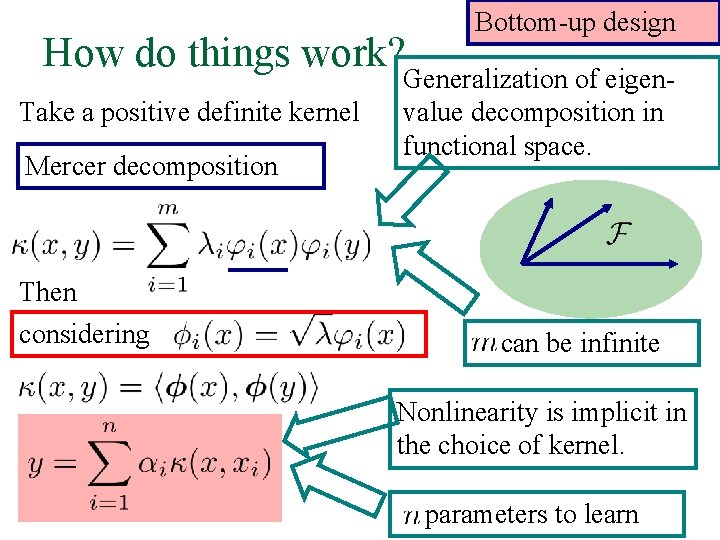
How do things work? Take a positive definite kernel Mercer decomposition Then considering Bottom-up design Generalization of eigenvalue decomposition in functional space. can be infinite Nonlinearity is implicit in the choice of kernel. parameters to learn

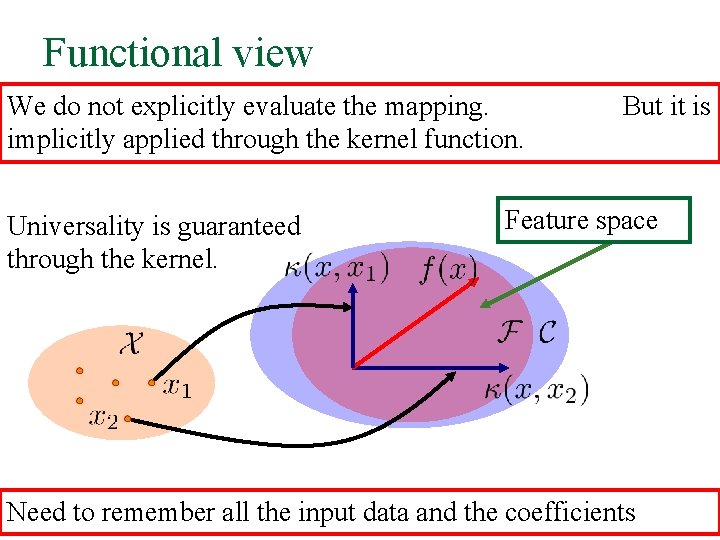
Functional view We do not explicitly evaluate the mapping. implicitly applied through the kernel function. Universality is guaranteed through the kernel. But it is Feature space Need to remember all the input data and the coefficients

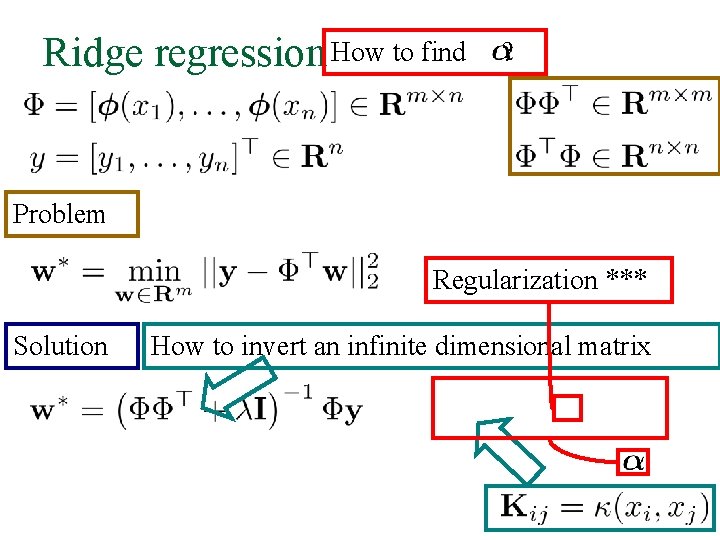
Ridge regression How to find ? Problem Regularization *** Solution How to invert an infinite dimensional matrix

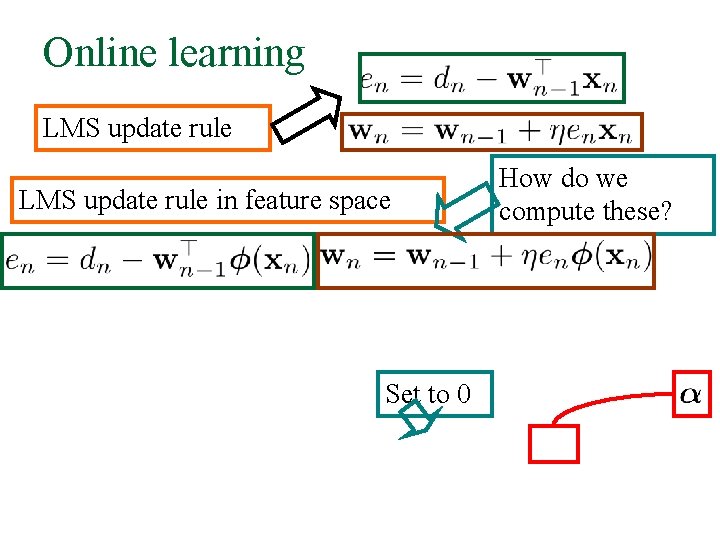
Online learning LMS update rule in feature space Set to 0 How do we compute these?

Kernel-LMS Initialize 1. Need to choose a kernel 2. Need to select step size 3. Need to store 4. No regularization *** Iterate for 5. time complexity for each iteration Unkwown is the largest eigenvalue of

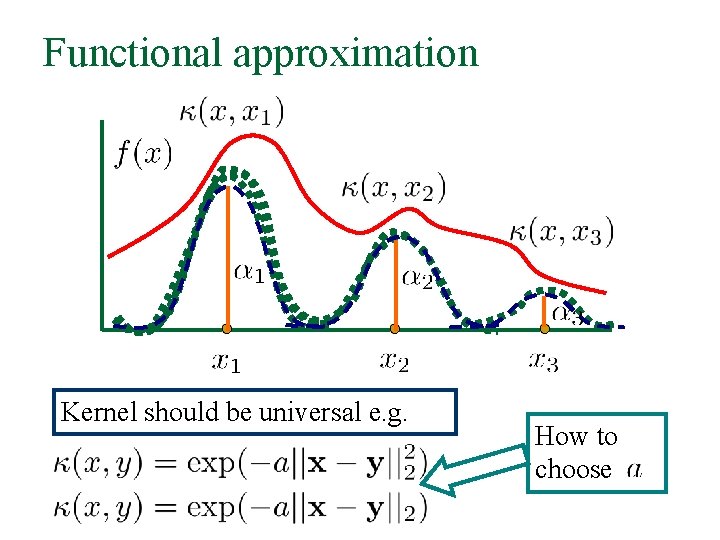
Functional approximation Kernel should be universal e. g. How to choose

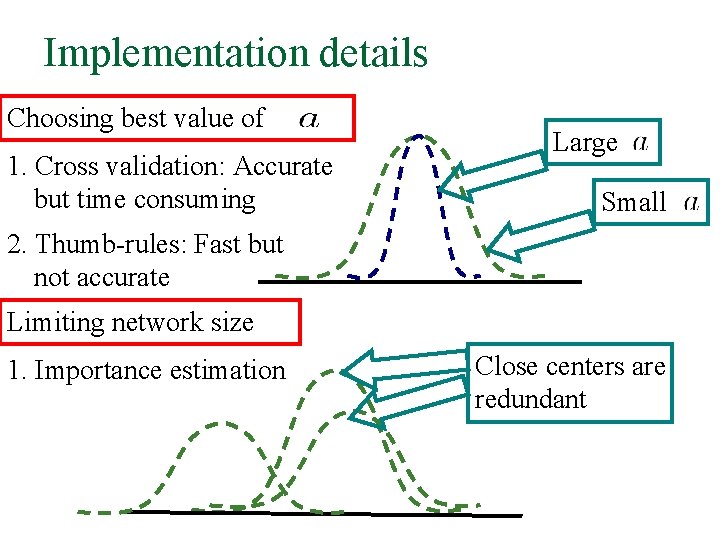
Implementation details Choosing best value of 1. Cross validation: Accurate but time consuming Large Small 2. Thumb-rules: Fast but not accurate Limiting network size 1. Importance estimation Close centers are redundant

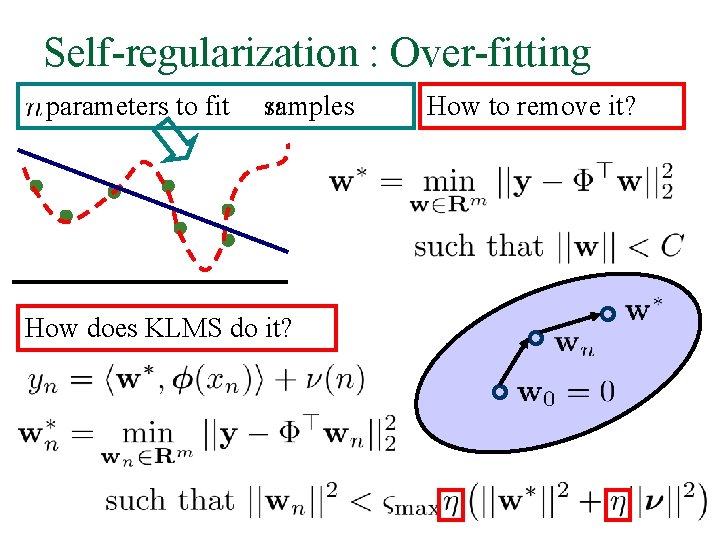
Self-regularization : Over-fitting parameters to fit samples How does KLMS do it? How to remove it?

Ill-posed-ness appears due to small singular values in the autocorrelation matrix while taking inverse How to remove it? Weight the inverse of the small singular values Tikhonov regularization Solve e. g.

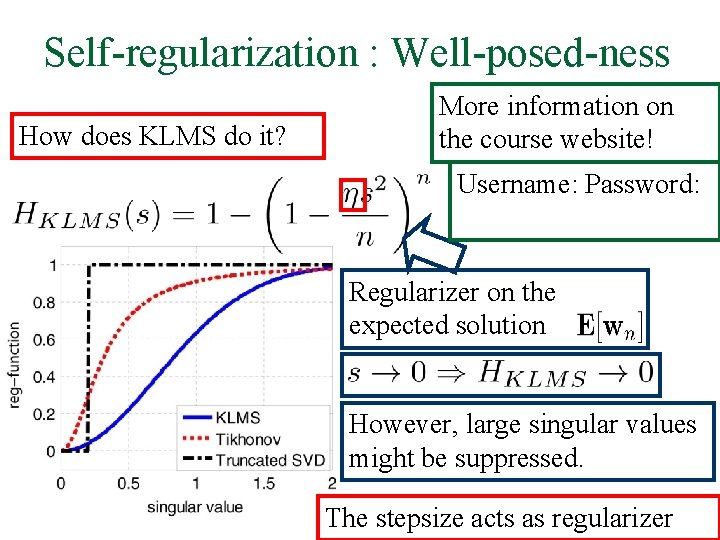
Self-regularization : Well-posed-ness How does KLMS do it? More information on the course website! Username: Password: Regularizer on the expected solution However, large singular values might be suppressed. The stepsize acts as regularizer