KDTrees CMSC 420 Goodbye Comparables The K in

KD-Trees CMSC 420

Goodbye Comparables! •

The ‘K’ in KD-Tree • KD-Trees were invented by Dr. Jon Bentley • The phrase “KD- Trees” is kind of a misnomer • K is really a strictly positive integer, with K = 1 being a classic BST with all of its good and bad characteristics. • But the term “KD-Tree” prevails instead of 2 D – Tree, 3 D – Tree, etc. • As K grows larger, some operations become more expensive.

Speaking of operations… •

KD-Trees: intuition • No matter what K is, the KD-Tree will always look like a binary tree. • That is, a tree with fanout exactly two. • Levels of the tree will be associated with a different dimension! • • Root level with x coordinate. Children of root with y coordinate. Grandchildren of root with z coordinate …. • Levels “wrap around” dimensions: after K levels, we fall back to x, then to y and so on.
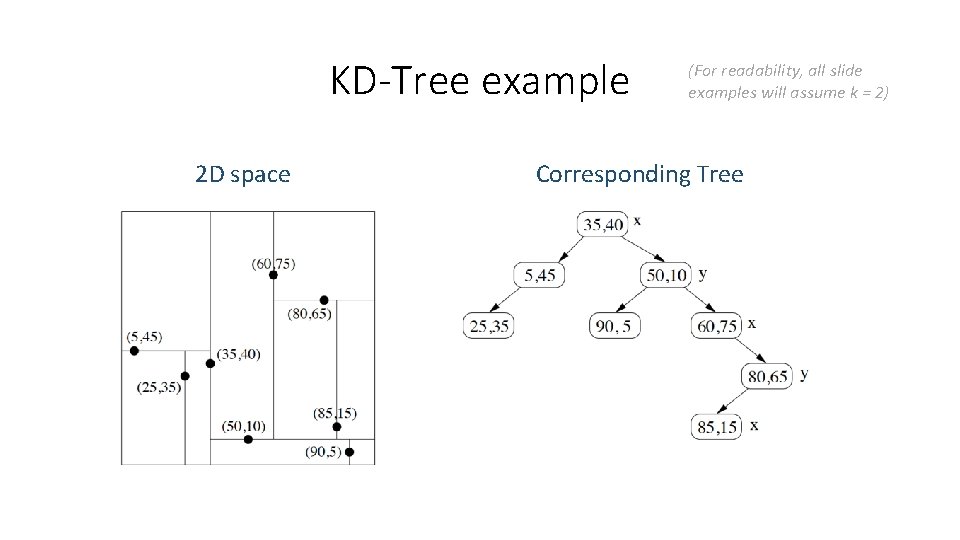
KD-Tree example 2 D space (For readability, all slide examples will assume k = 2) Corresponding Tree
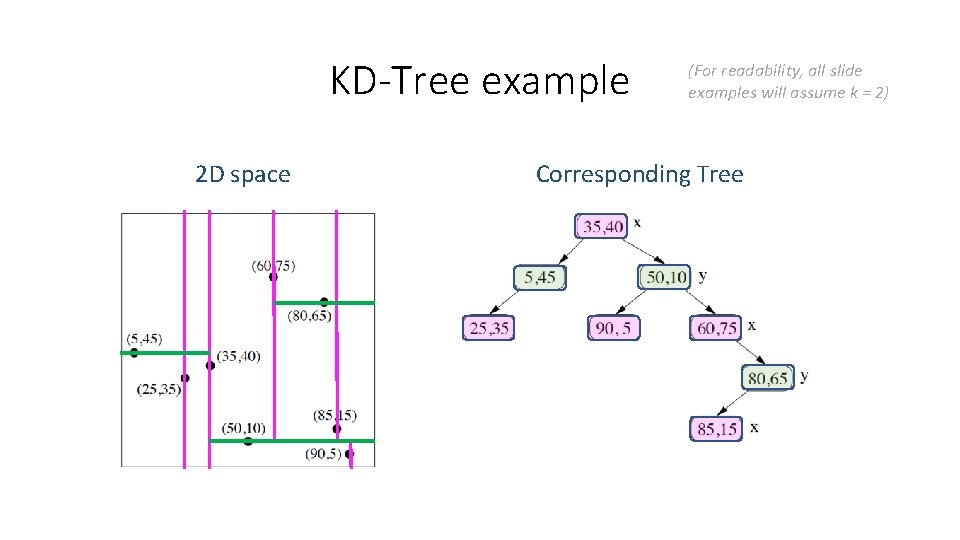
KD-Tree example 2 D space (For readability, all slide examples will assume k = 2) Corresponding Tree

Insertion • When we insert, we have to be careful: a) To alternate our dimensions! b) To obey the BST property; nodes whose current dimension value is bigger than or equal to the current node’s current dimension value should be inserted into the right subtree, and vice versa. • Note that this isn’t saying anything about duplicate keys!
Insertion Examples 2 D space Corresponding Tree root null
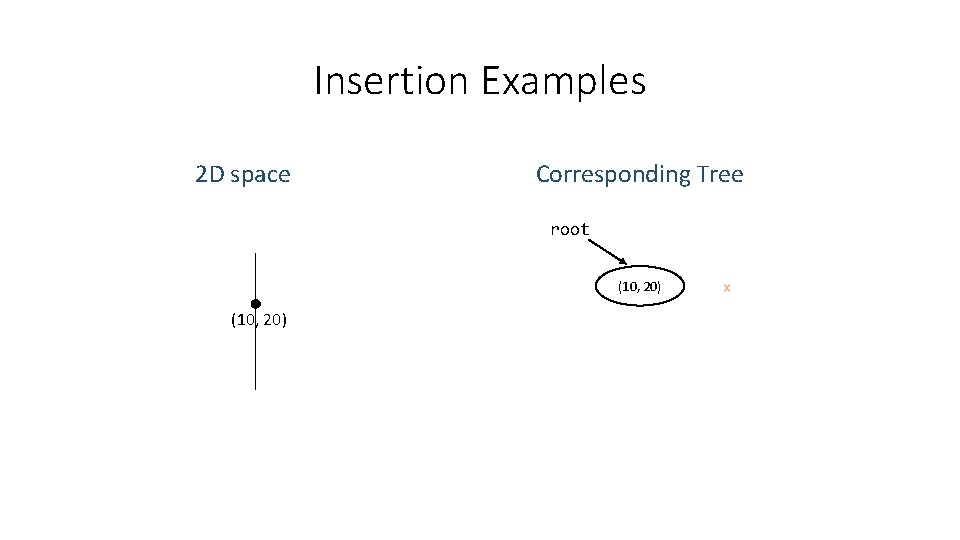
Insertion Examples 2 D space Corresponding Tree root (10, 20) x

Insertion Examples Corresponding Tree 2 D space root (10, 20) 5 < 10 x (10, 20) (5, 10) y
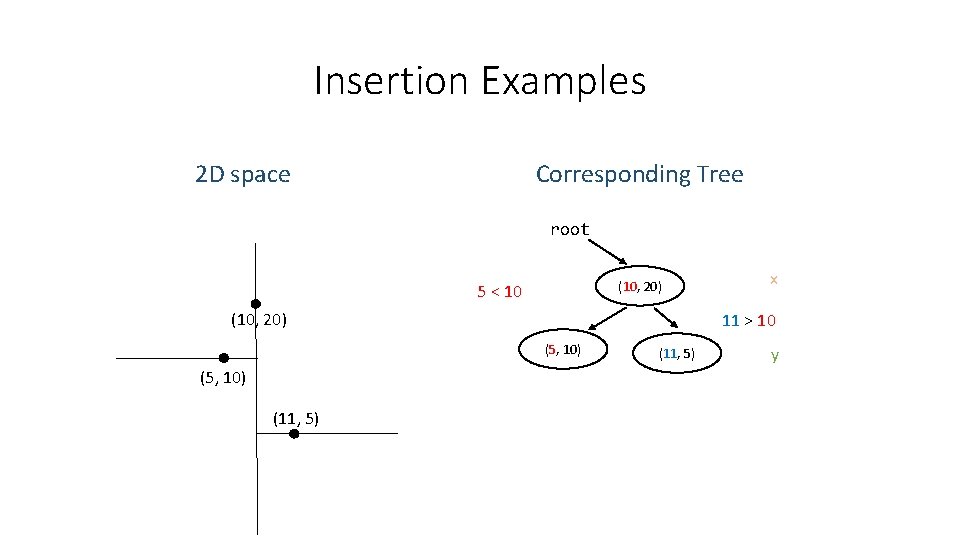
Insertion Examples Corresponding Tree 2 D space root (10, 20) 5 < 10 (10, 20) 11 > 10 (5, 10) (11, 5) x (11, 5) y
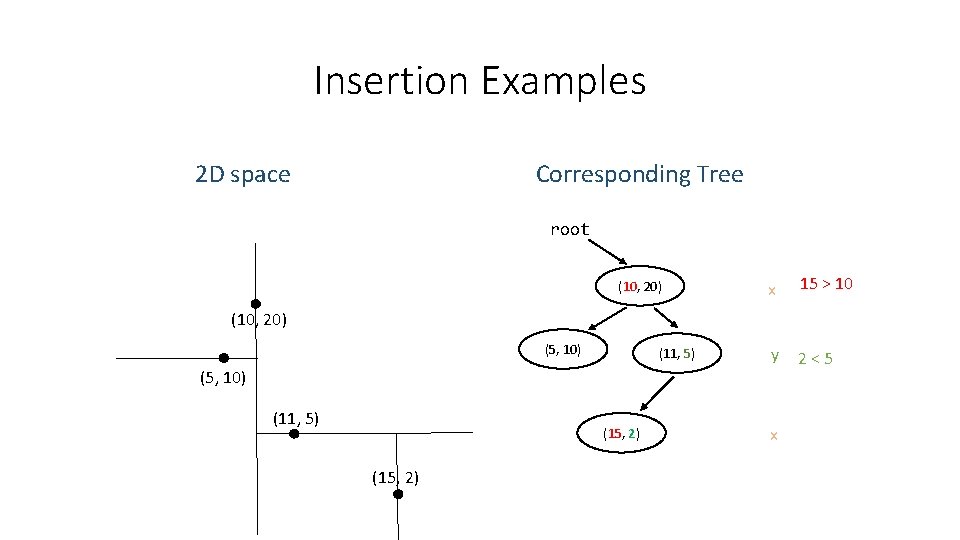
Insertion Examples Corresponding Tree 2 D space root (10, 20) x 15 > 10 y 2 < 5 (10, 20) (5, 10) (11, 5) (15, 2) x
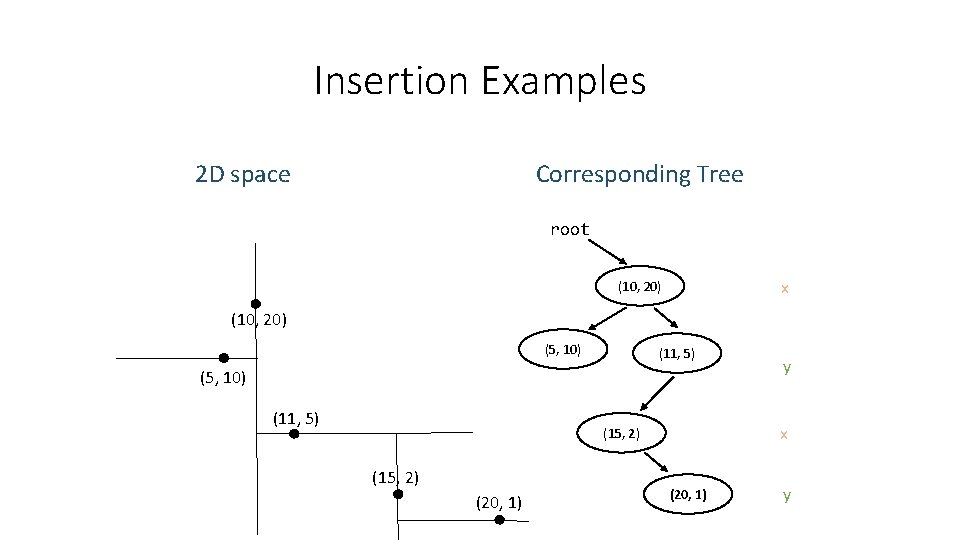
Insertion Examples Corresponding Tree 2 D space root x (10, 20) (5, 10) (11, 5) x (15, 2) (20, 1) y
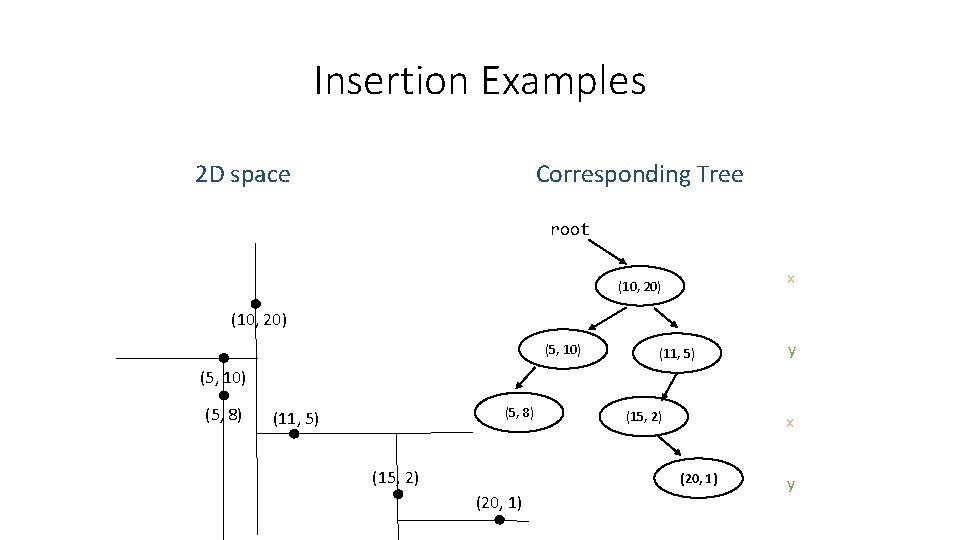
Insertion Examples Corresponding Tree 2 D space root x (10, 20) (5, 10) (11, 5) y (5, 10) (5, 8) (11, 5) (15, 2) x (20, 1) y

Let’s write some code! •

Let’s write some code! private int dimensions; private class Node { Node(KDPoint p){. . . } KDPoint get. Point(){. . . } } public void insert(KDPoint p){ root = insert(root, p, 0); // ‘ 0’ stands for ‘x’ } private Node insert(Node curr, KDPoint p, int curr. Dim){ /* Fill this in for me please! */ }

Let’s write some code! private int dimensions; private class Node { Node(KDPoint p){. . . } KDPoint get. Point(){. . . } } public void insert(KDPoint p){ } root = insert(root, p, 0); // ‘ 0’ stands for ‘x’ private Node insert(Node curr, KDPoint p, int curr. Dim){ if(curr == null) return new Node(p); int next. Dim = (curr. Dim + 1) % dimensions; // Precompute for clarity if(p. get(curr. Dim) >= curr. get. Point(). get(curr. Dim)) // Go right curr. right = insert(curr. right, p, next. Dim); else // Input point’s current dimension value smaller, go Left curr. left = insert(curr. left, p, next. Dim); }

Let’s write some code! private int dimensions; private class Node { Node(KDPoint p){. . . } KDPoint get. Point(){. . . } } public void insert(KDPoint p){ } root = insert(root, p, 0); // ‘ 0’ stands for ‘x’ Depending on how you design your private components, this implementation can, more or less, be used verbatim in your project! private Node insert(Node curr, KDPoint p, int curr. Dim){ if(curr == null) return new Node(p); int next. Dim = (curr. Dim + 1) % dimensions; // Precompute for clarity if(p. get(curr. Dim) >= curr. get. Point(). get(curr. Dim)) // Go right curr. right = insert(curr. right, p, next. Dim); else // Input point’s current dimension value smaller, go Left curr. left = insert(curr. left, p, next. Dim); return curr; }

Deletion • Remember the BST cases: 1. Left and right child null? Return null (node gets erased) 2. Left child non-null and right child null? Replace node with left subtree. 3. Right child non-null? Exchange node’s key with that of the inorder successor node, and recursively delete that key from your right subtree. • This won’t fly in KD-Trees, for two reasons: • In case 2, replacing the node with the left subtree changes the semantics of every one of the left subtree’s nodes’ dimension splitting! • In case 3, the notion of an “inorder successor” is now hazy at best (remember, we’ve moved away from Comparables!)

Deletion • Remember the BST cases: 1. Left and right child null? Return null (node gets erased) 2. Left child non-null and right child null? Replace node with left subtree. 3. Right child non-null? Exchange node’s key with that of the inorder successor node, and recursively delete that key from your right subtree. • This won’t fly in KD-Trees, for two reasons: • In case 2, replacing the node with the left subtree changes the semantics of every one of the left subtree’s nodes’ dimension splitting! • In case 3, the notion of an “inorder successor” is now hazy at best (remember, we’ve moved away from Comparables!) • So what can we do?
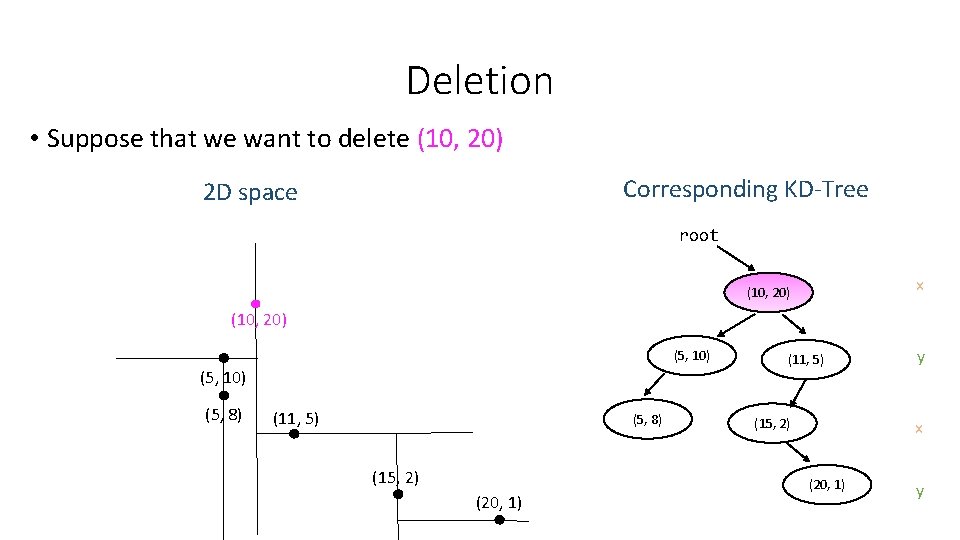
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space root x (10, 20) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) (11, 5) (15, 2) y x (20, 1) y
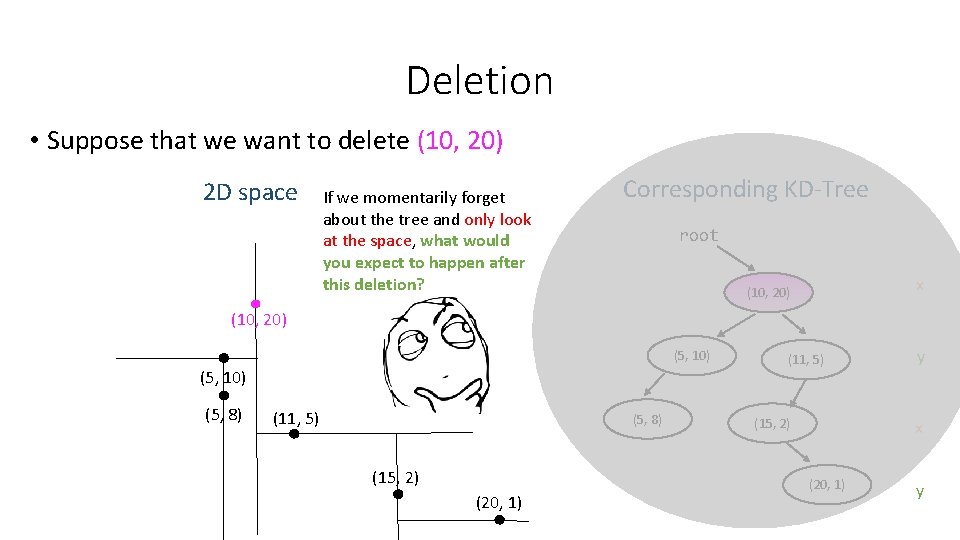
Deletion • Suppose that we want to delete (10, 20) 2 D space If we momentarily forget about the tree and only look at the space, what would you expect to happen after this deletion? Corresponding KD-Tree root x (10, 20) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) (11, 5) (15, 2) y x (20, 1) y
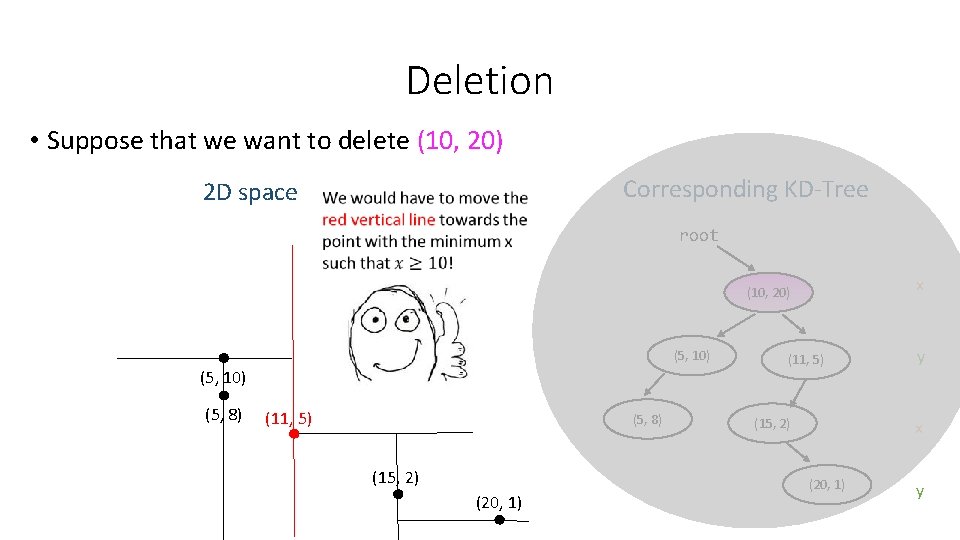
Deletion • Suppose that we want to delete (10, 20) 2 D space Corresponding KD-Tree root x (10, 20) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) (11, 5) (15, 2) y x (20, 1) y
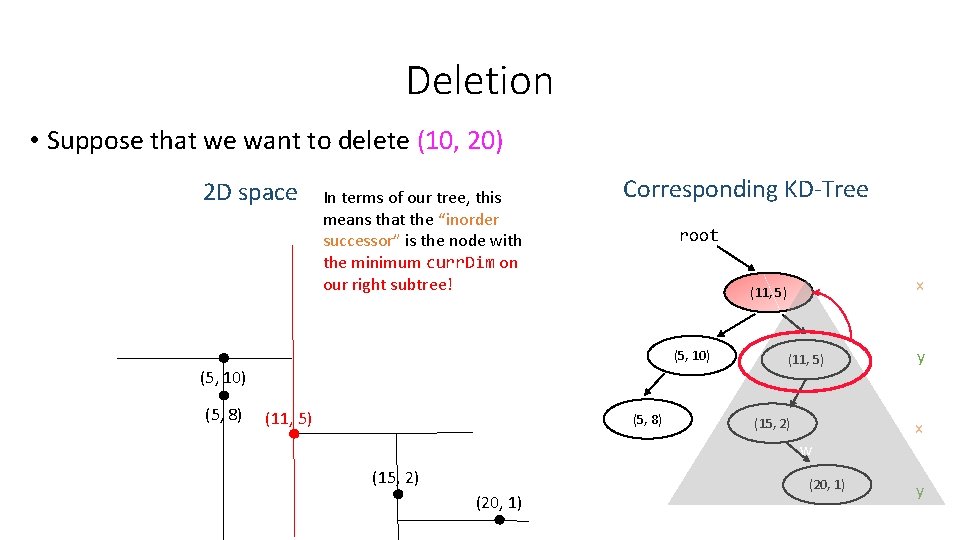
Deletion • Suppose that we want to delete (10, 20) 2 D space In terms of our tree, this means that the “inorder successor” is the node with the minimum curr. Dim on our right subtree! Corresponding KD-Tree root (5, 10) (5, 8) (11, 5) x (11, 5) (5, 8) (11, 5) (15, 2) w (15, 2) (20, 1) y x y
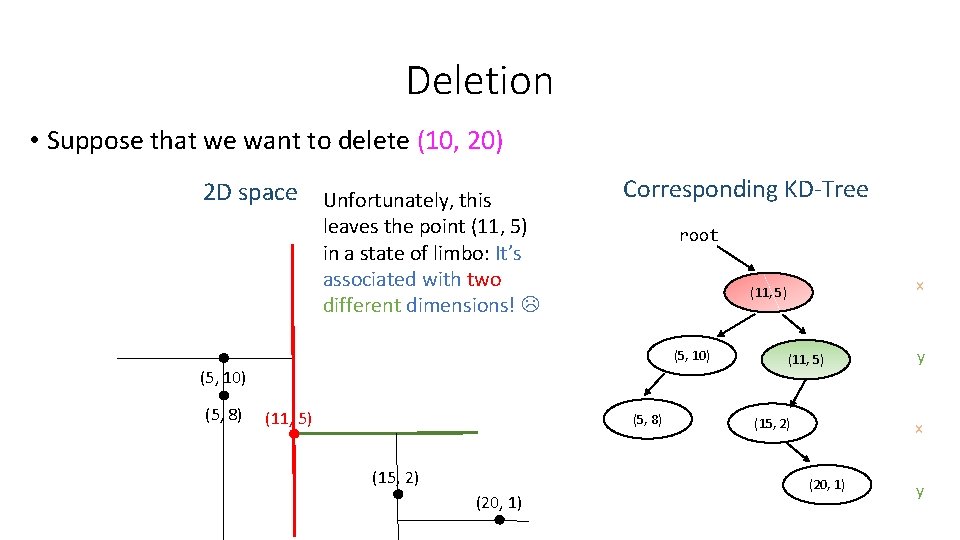
Deletion • Suppose that we want to delete (10, 20) 2 D space Unfortunately, this Corresponding KD-Tree leaves the point (11, 5) in a state of limbo: It’s associated with two different dimensions! root (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) x (11, 5) (15, 2) y x (20, 1) y
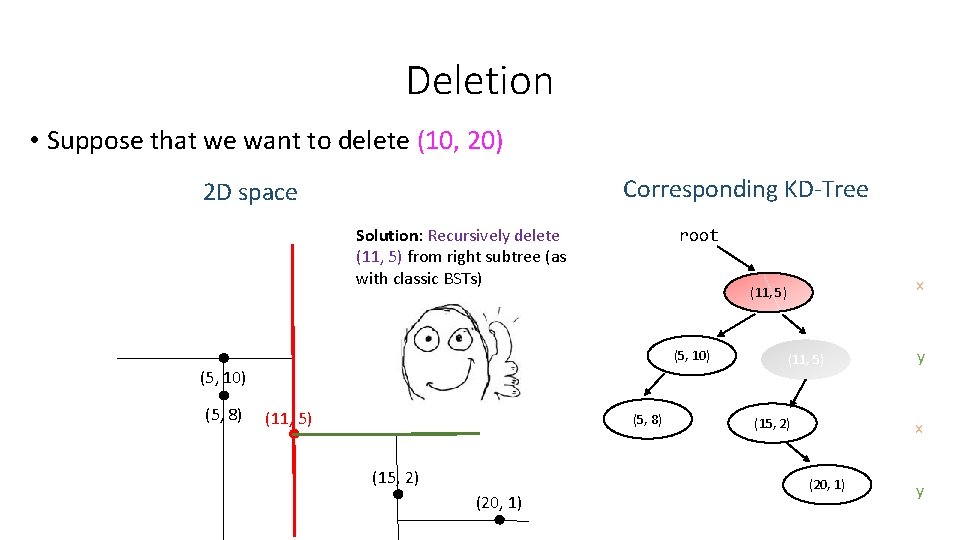
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space Solution: Recursively delete (11, 5) from right subtree (as with classic BSTs) root (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) x (11, 5) (15, 2) y x (20, 1) y
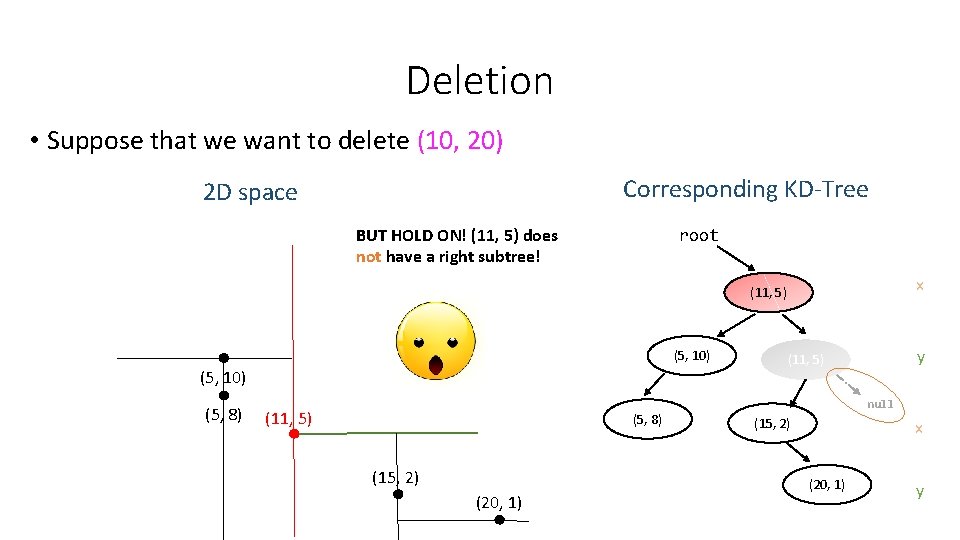
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space BUT HOLD ON! (11, 5) does not have a right subtree! root x (11, 5) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) y (11, 5) null (15, 2) x (20, 1) y
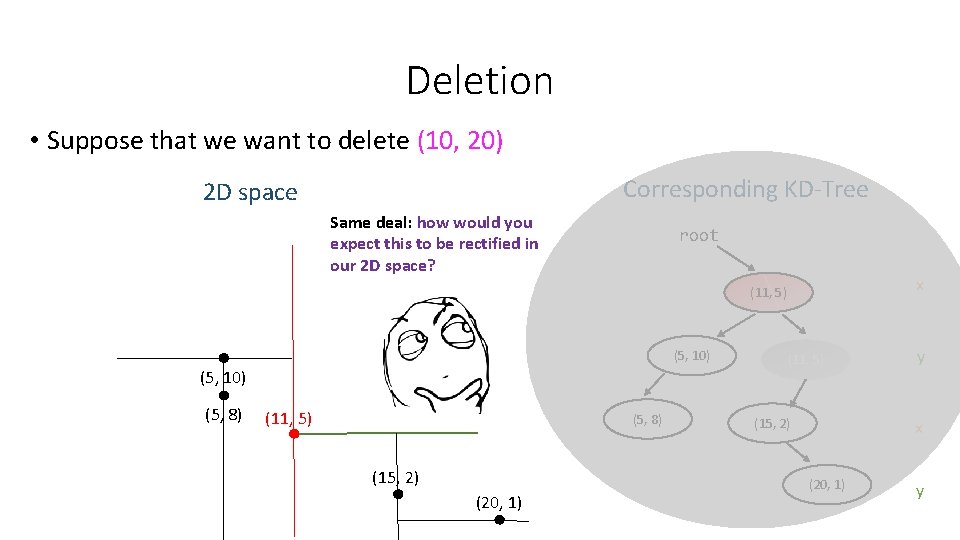
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space Same deal: how would you expect this to be rectified in our 2 D space? root x (11, 5) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) (11, 5) (15, 2) y x (20, 1) y
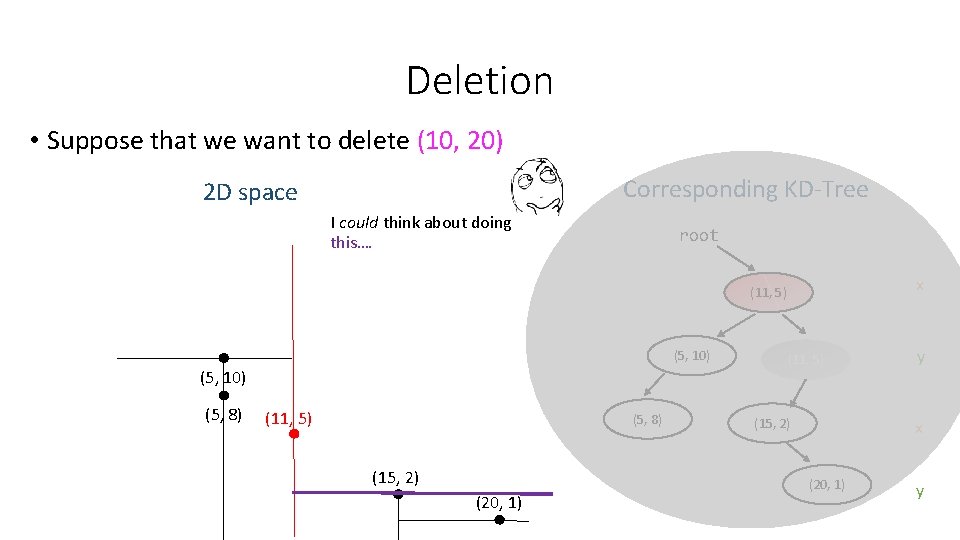
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space I could think about doing this…. root x (11, 5) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) (11, 5) (15, 2) y x (20, 1) y
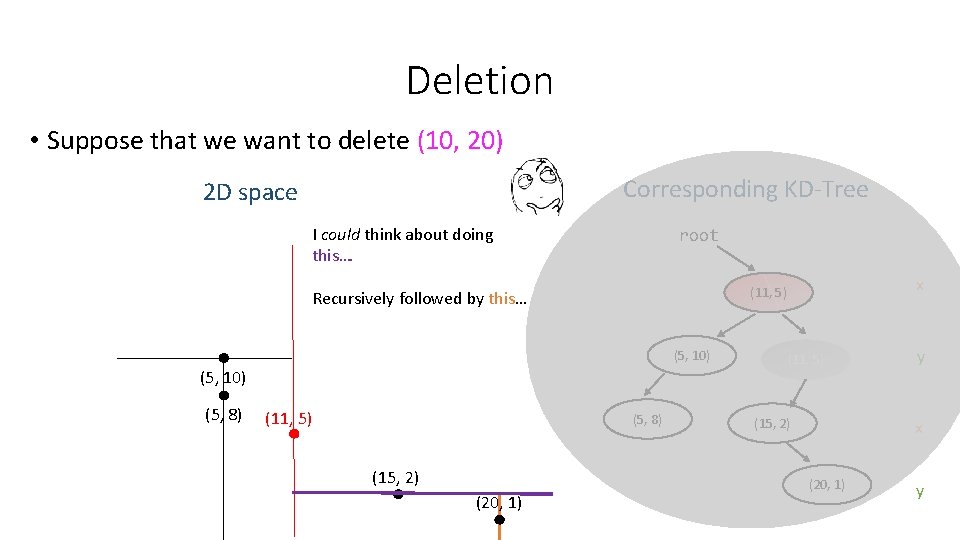
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space I could think about doing this…. root Recursively followed by this… (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) x (11, 5) (15, 2) y x (20, 1) y
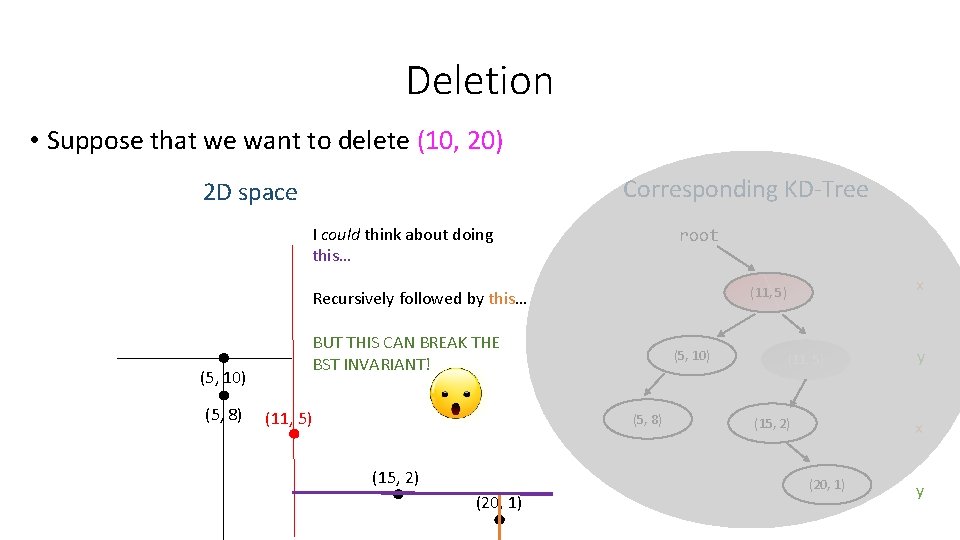
Deletion • Suppose that we want to delete (10, 20) Corresponding KD-Tree 2 D space I could think about doing this… root Recursively followed by this… (5, 10) (5, 8) BUT THIS CAN BREAK THE BST INVARIANT! (11, 5) (5, 10) (5, 8) (15, 2) (20, 1) x (11, 5) (15, 2) y x (20, 1) y
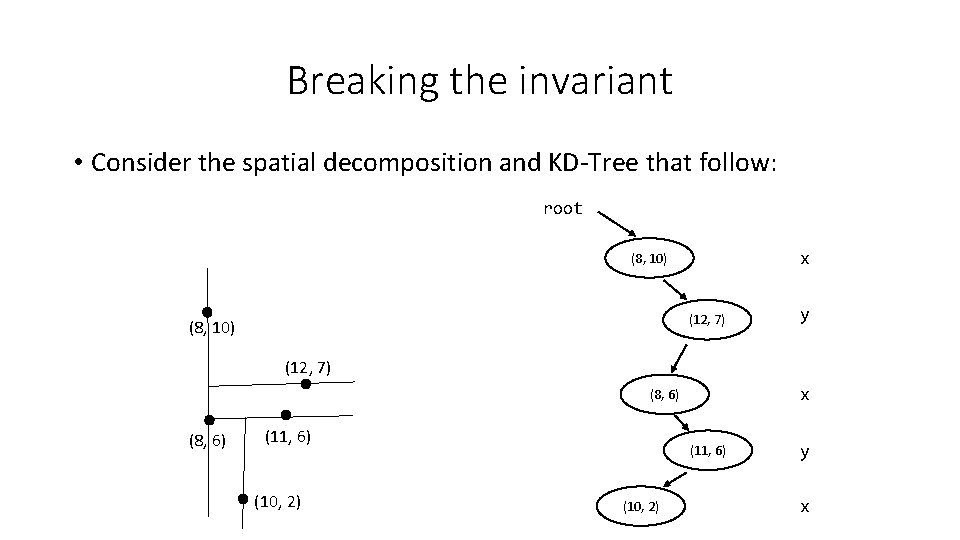
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root x (8, 10) (12, 7) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
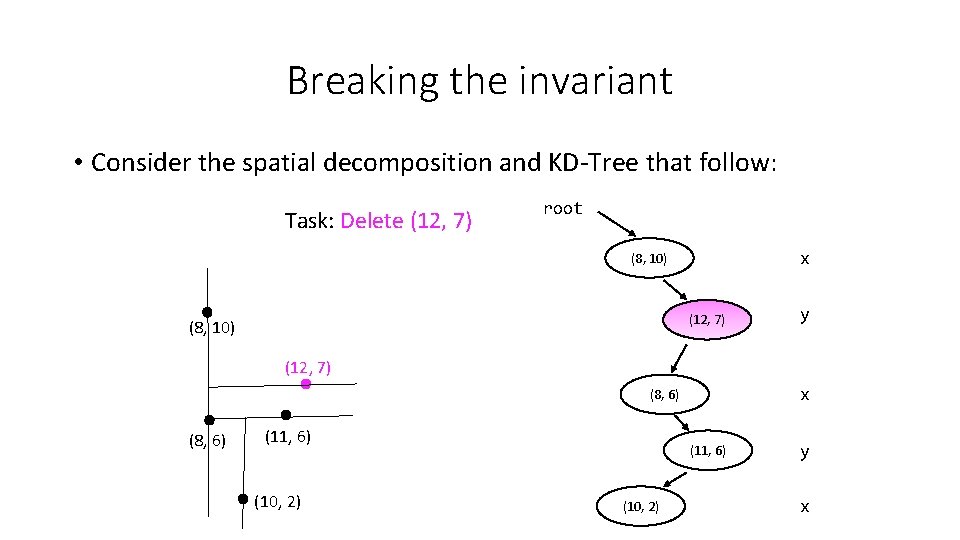
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: Task: Delete (12, 7) root x (8, 10) (12, 7) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
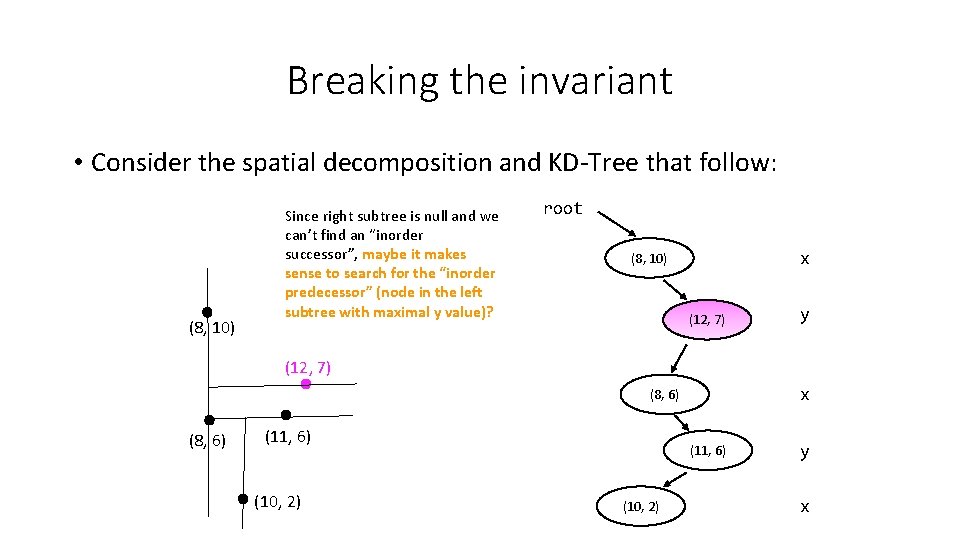
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: (8, 10) Since right subtree is null and we can’t find an “inorder successor”, maybe it makes sense to search for the “inorder predecessor” (node in the left subtree with maximal y value)? root x (8, 10) (12, 7) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
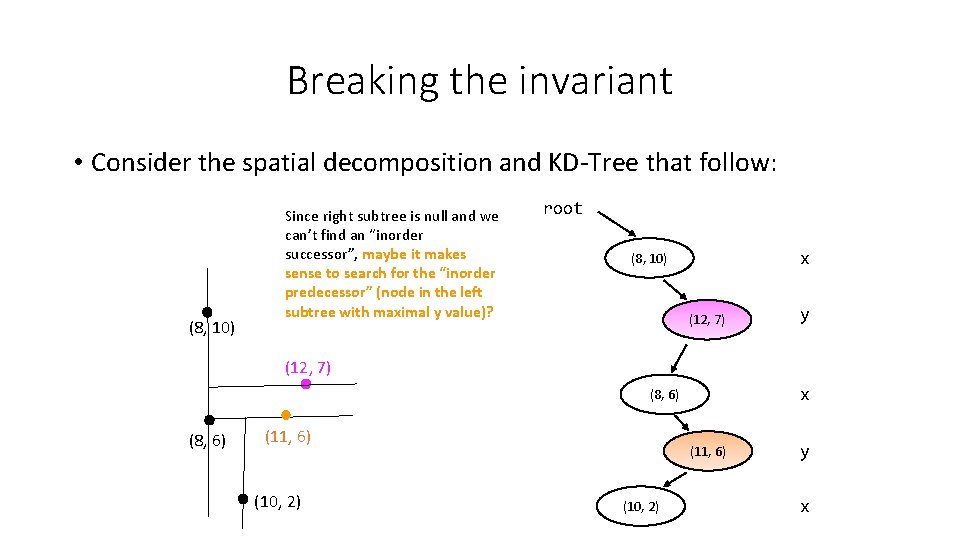
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: (8, 10) Since right subtree is null and we can’t find an “inorder successor”, maybe it makes sense to search for the “inorder predecessor” (node in the left subtree with maximal y value)? root x (8, 10) (12, 7) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
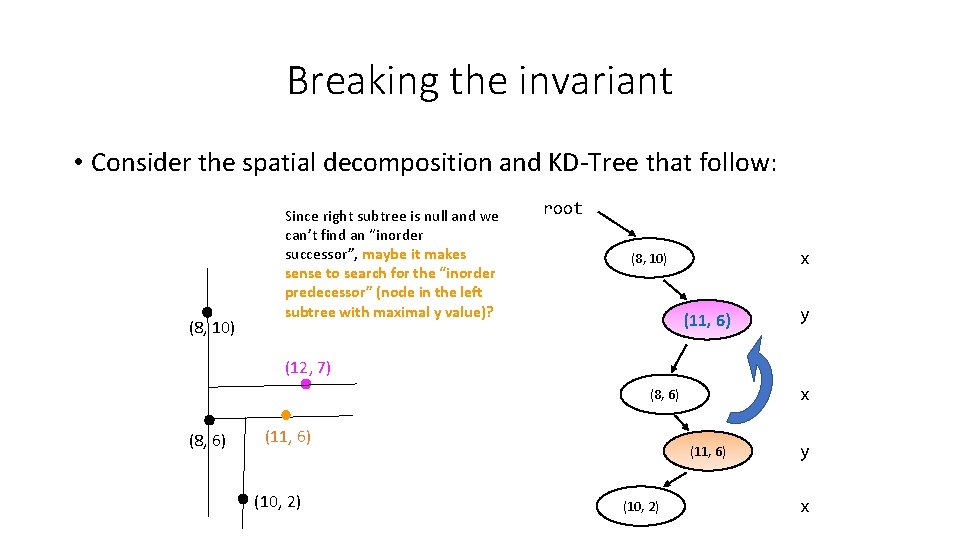
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: (8, 10) Since right subtree is null and we can’t find an “inorder successor”, maybe it makes sense to search for the “inorder predecessor” (node in the left subtree with maximal y value)? root x (8, 10) (11, 6) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
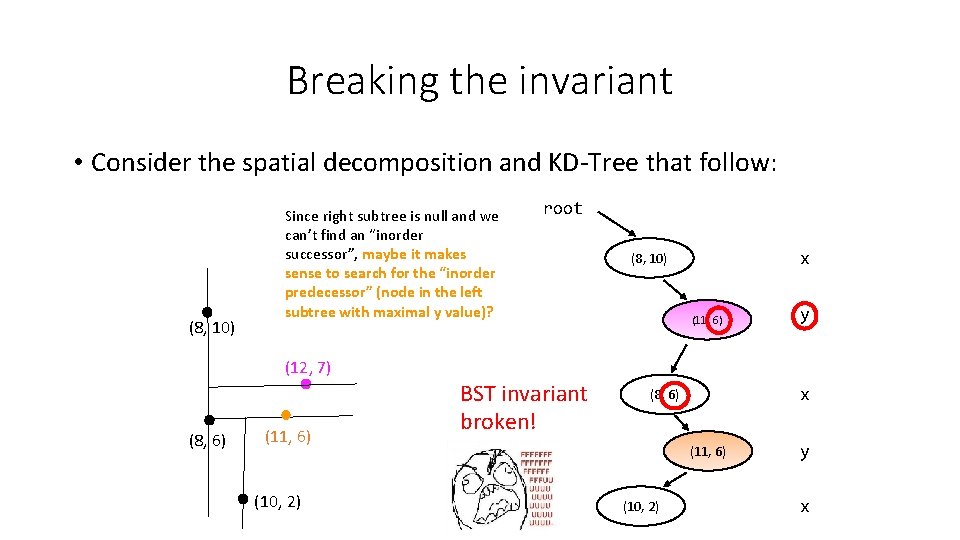
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: (8, 10) Since right subtree is null and we can’t find an “inorder successor”, maybe it makes sense to search for the “inorder predecessor” (node in the left subtree with maximal y value)? (12, 7) (8, 6) (11, 6) (10, 2) root BST invariant broken! x (8, 10) (11, 6) x (8, 6) (11, 6) (10, 2) y y x
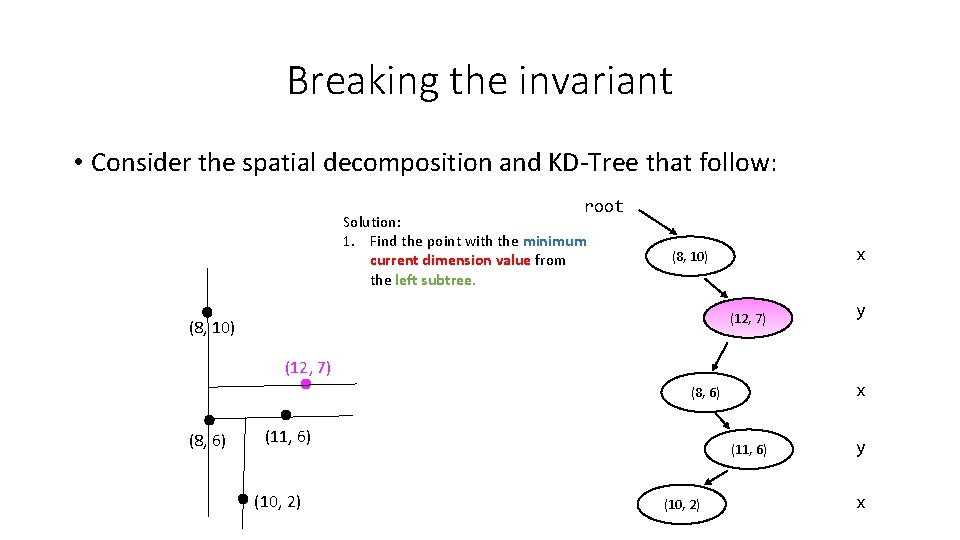
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. x (8, 10) (12, 7) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
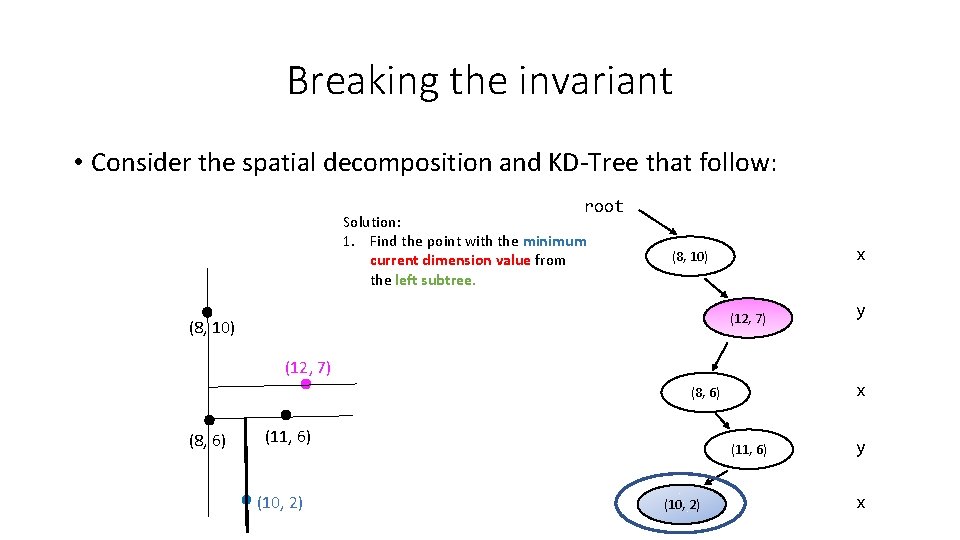
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. x (8, 10) (12, 7) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
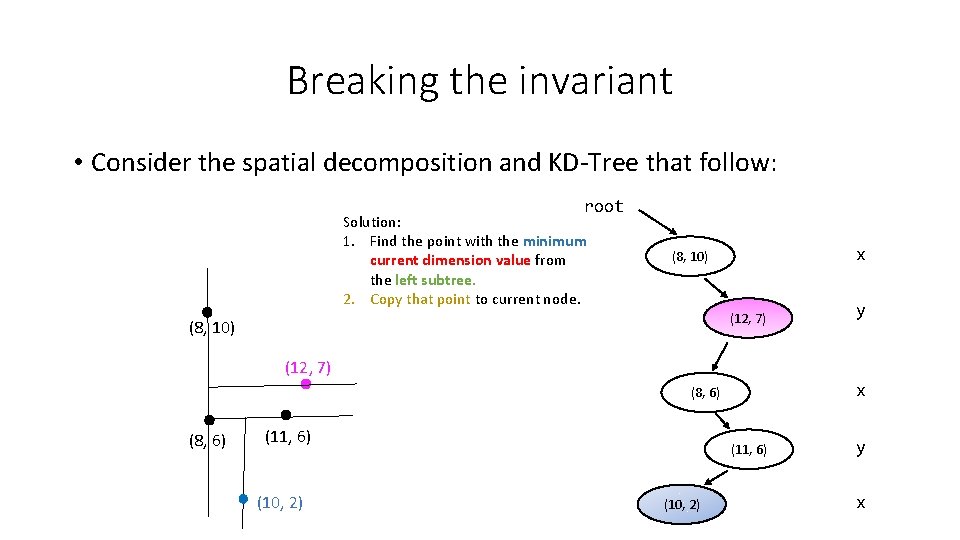
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. x (8, 10) (12, 7) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
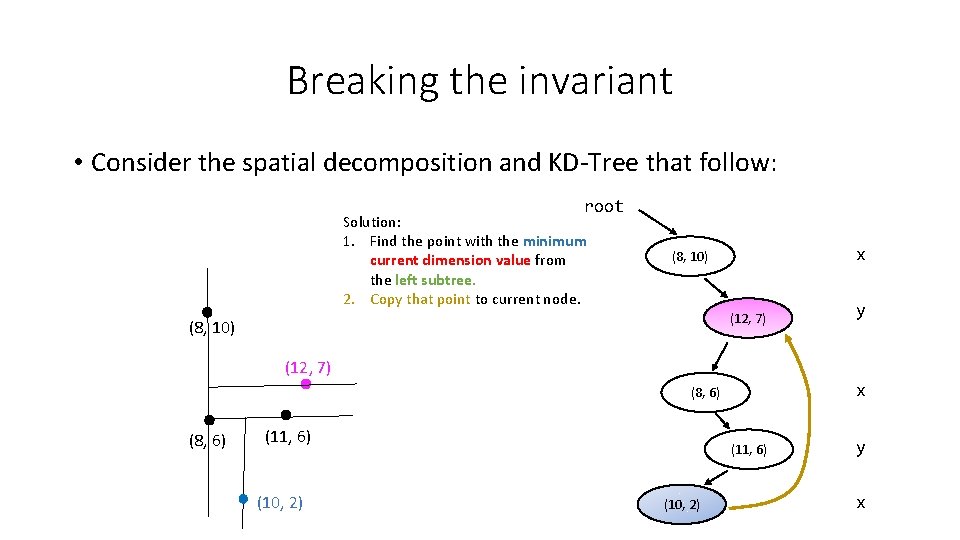
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. x (8, 10) (12, 7) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
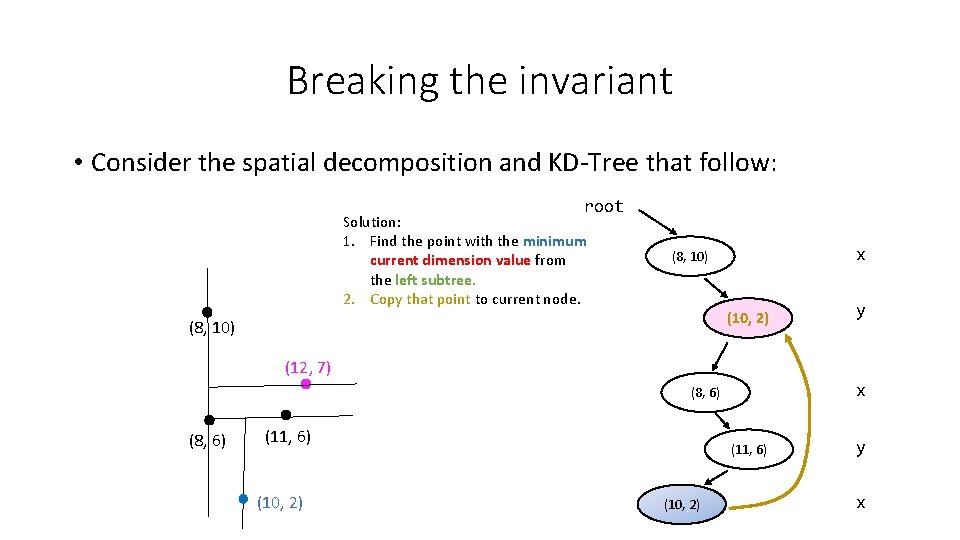
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. x (8, 10) (10, 2) (8, 10) y (12, 7) x (8, 6) (11, 6) (10, 2) y x
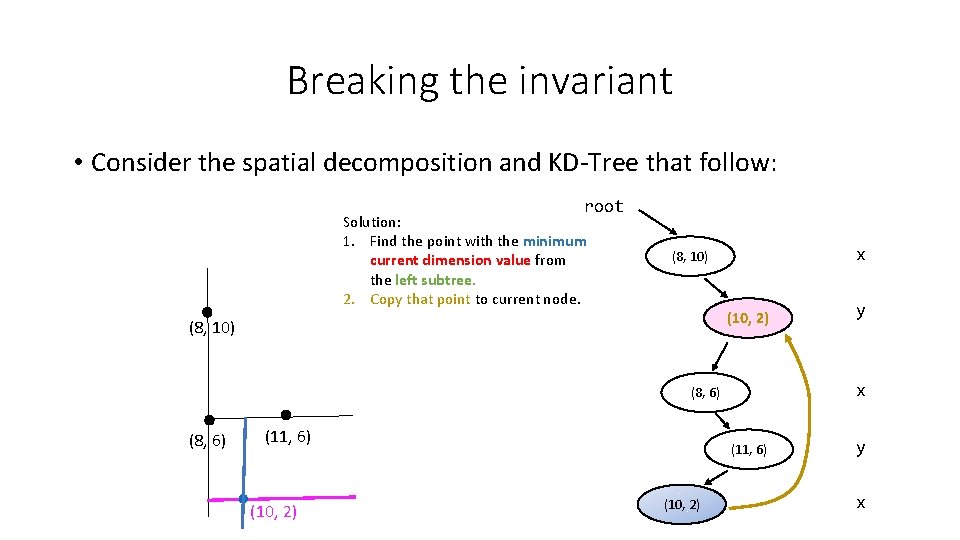
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. x (8, 10) (10, 2) (8, 10) x (8, 6) (11, 6) (10, 2) y y x
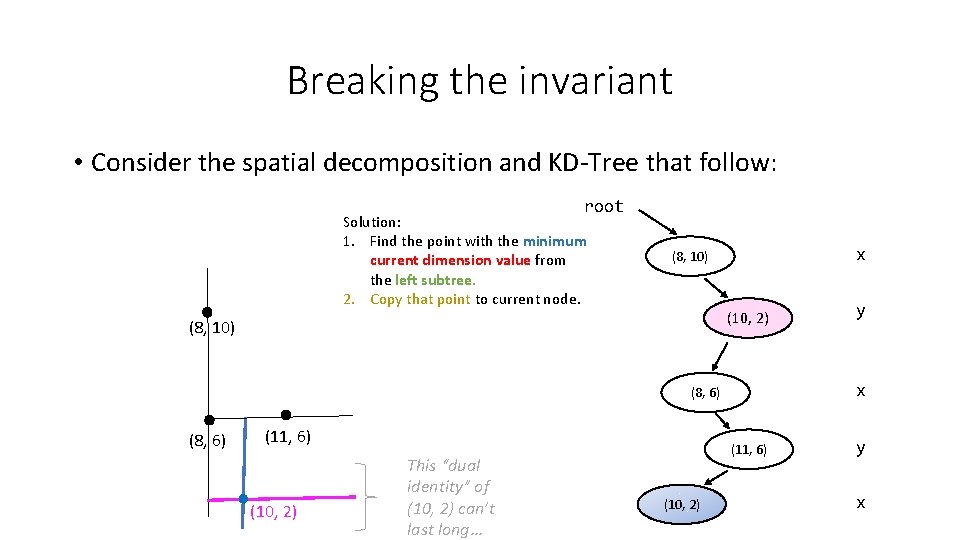
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. x (8, 10) (10, 2) (8, 10) x (8, 6) (11, 6) (10, 2) This “dual identity” of (10, 2) can’t last long… (11, 6) (10, 2) y y x
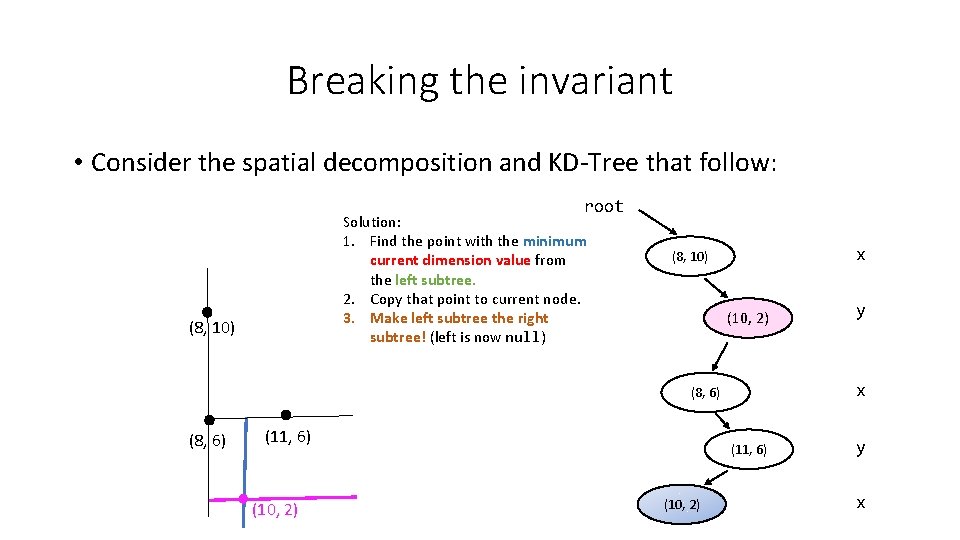
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. 3. Make left subtree the right subtree! (left is now null) (8, 10) x (8, 10) (10, 2) x (8, 6) (11, 6) (10, 2) y y x
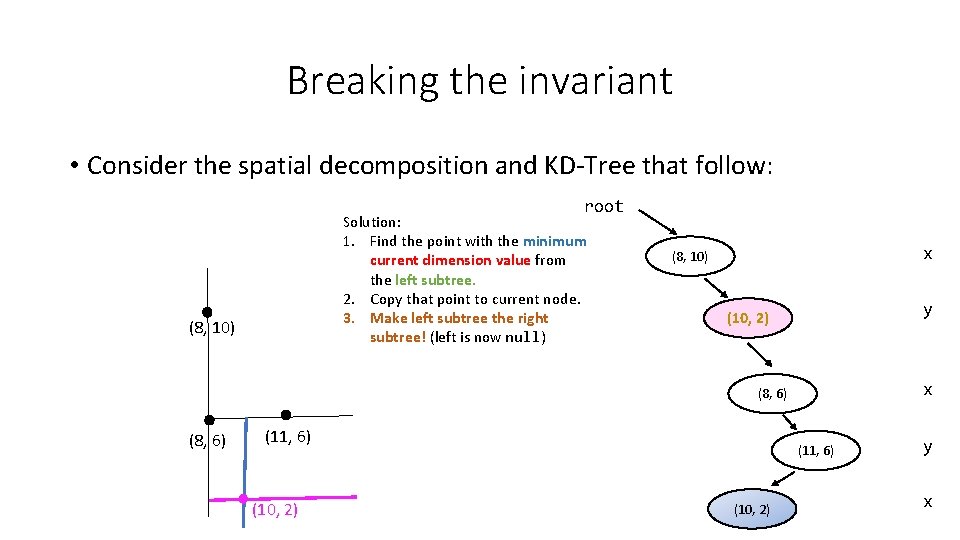
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. 3. Make left subtree the right subtree! (left is now null) (8, 10) x (8, 10) y (10, 2) x (8, 6) (11, 6) (10, 2) y x
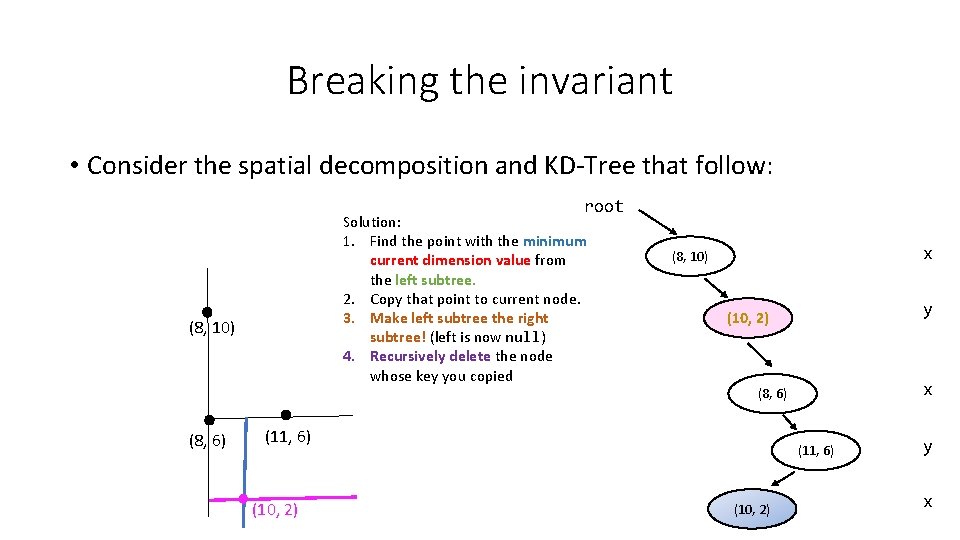
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. 3. Make left subtree the right subtree! (left is now null) 4. Recursively delete the node whose key you copied (8, 10) x (8, 10) y (10, 2) x (8, 6) (11, 6) (10, 2) y x
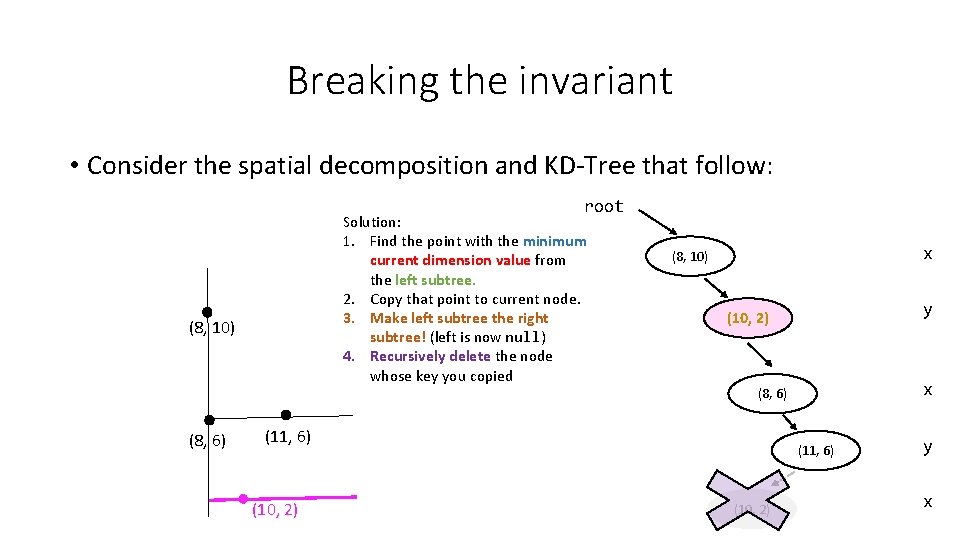
Breaking the invariant • Consider the spatial decomposition and KD-Tree that follow: root Solution: 1. Find the point with the minimum current dimension value from the left subtree. 2. Copy that point to current node. 3. Make left subtree the right subtree! (left is now null) 4. Recursively delete the node whose key you copied (8, 10) x (8, 10) y (10, 2) x (8, 6) (11, 6) (10, 2) y x
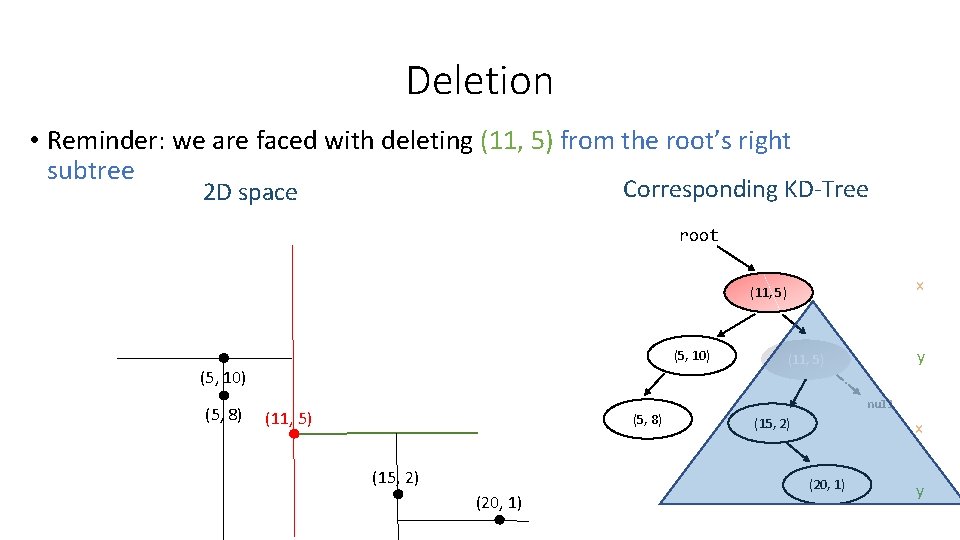
Deletion • Reminder: we are faced with deleting (11, 5) from the root’s right subtree Corresponding KD-Tree 2 D space root x (11, 5) (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) y (11, 5) null (15, 2) x (20, 1) y
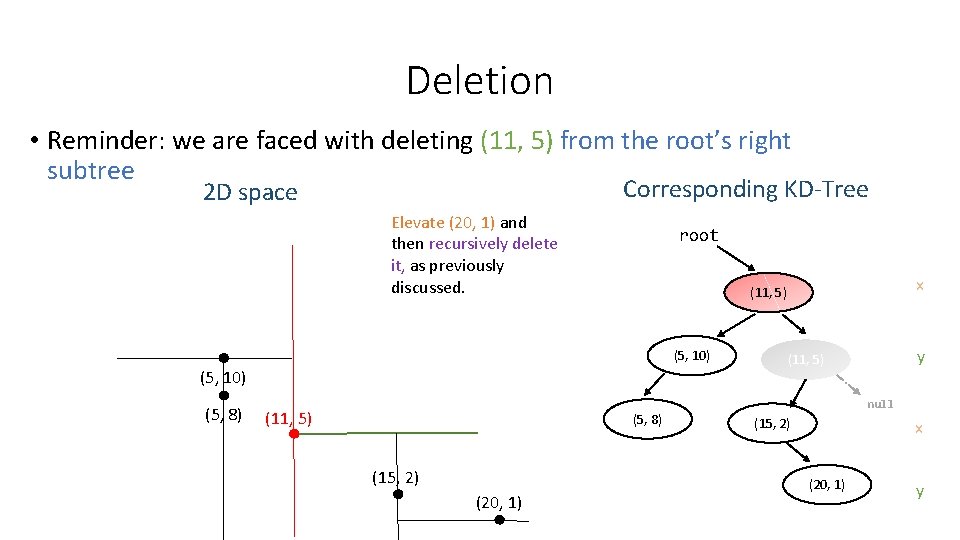
Deletion • Reminder: we are faced with deleting (11, 5) from the root’s right subtree Corresponding KD-Tree 2 D space Elevate (20, 1) and then recursively delete it, as previously discussed. root (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) (20, 1) x (11, 5) y (11, 5) null (15, 2) x (20, 1) y
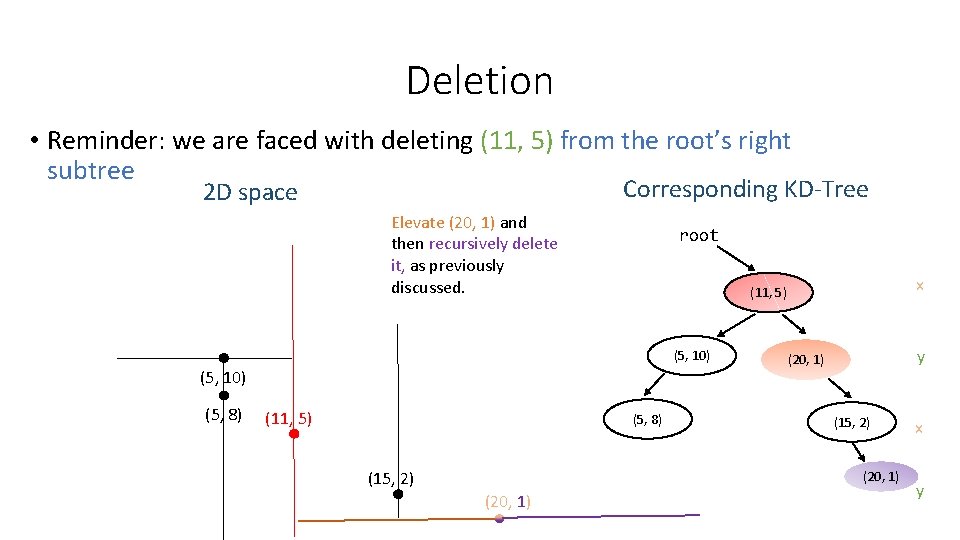
Deletion • Reminder: we are faced with deleting (11, 5) from the root’s right subtree Corresponding KD-Tree 2 D space Elevate (20, 1) and then recursively delete it, as previously discussed. root (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) x (11, 5) y (20, 1) (15, 2) (20, 1) x y
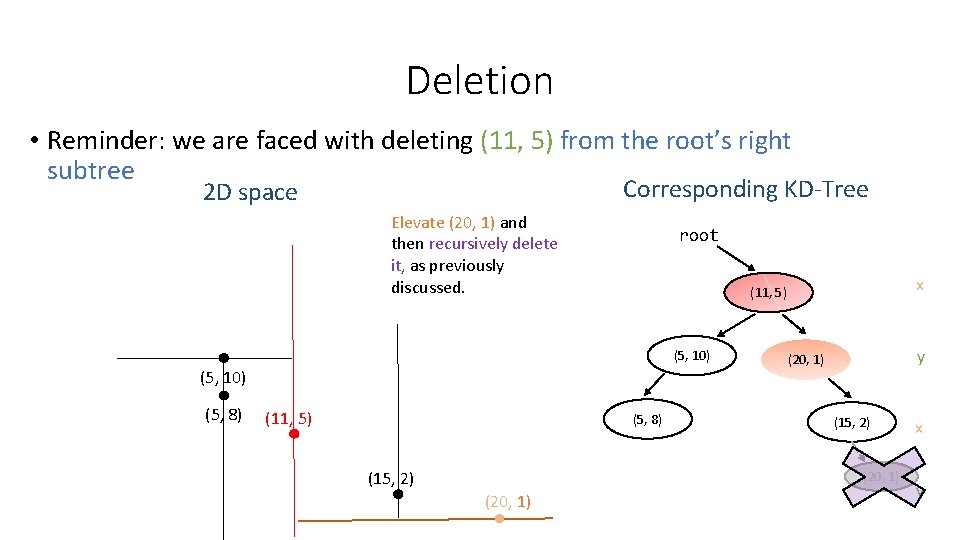
Deletion • Reminder: we are faced with deleting (11, 5) from the root’s right subtree Corresponding KD-Tree 2 D space Elevate (20, 1) and then recursively delete it, as previously discussed. root (5, 10) (5, 8) (11, 5) (5, 8) (15, 2) x (11, 5) y (20, 1) (15, 2) (20, 1) x y

A more complex deletion

Code time! • Suppose that you have implemented a method find. Min with the following signature: Node find. Min(Node root, desired. Dim, curr. Dim) • Use the method to fill in the implementation of delete() below! It should return null if it fails to find the key. Node delete(KDPoint p, Node t, int curr. Dim){ /* Fill this in! */ }

Code time! Node find. Min(Node root, int desired. Dim, int curr. Dim) Node delete(KDPoint p, Node curr, int curr. Dim){ if(curr==null) return null; // Fell of the tree: failed search else if(curr. get. Point(). equals(p)) { // Found the key if(curr. right != null){ // Take replacement from right, recursively delete. curr. set. Point(find. Min(curr. right, curr. Dim, (curr. Dim + 1) % dimensions). get. Point()); curr. right = delete(curr. get. Point(), curr. right, (curr. Dim + 1) % dimensions); } else {// Take replacement from LEFT, recursively delete and swap trees! curr. set. Point(find. Min(curr. left, curr. Dim, (curr. Dim + 1) % dimensions). get. Point()); curr. right = delete(curr. get. Point(), curr. left, (curr. Dim + 1) % dimensions); curr. left = null; } } else if(curr. get. Point(). get(curr. Dim) < p. get(curr. Dim)){ curr. left = delete(p, curr. left, (curr. Dim + 1) % dimensions); } else { curr. right= delete(p, curr. right, (curr. Dim + 1) % dimensions); } return curr; }

Code time! Node find. Min(Node root, int desired. Dim, int curr. Dim) Node delete(KDPoint p, Node curr, int curr. Dim){ if(curr==null) return null; // Fell of the tree: failed search else if(curr. get. Point(). equals(p)) { // Found the key if(curr. right != null){ // Take replacement from right, recursively delete. curr. set. Point(find. Min(curr. right, curr. Dim, (curr. Dim + 1) % dimensions). get. Point()); curr. right = delete(curr. get. Point(), curr. right, (curr. Dim + 1) % dimensions); } else {// Take replacement from LEFT, recursively delete and swap trees! curr. set. Point(find. Min(curr. left, curr. Dim, (curr. Dim + 1) % dimensions). get. Point()); curr. right = delete(curr. get. Point(), curr. left, (curr. Dim + 1) % dimensions); curr. left = null; } } else if(curr. get. Point(). get(curr. Dim) < p. get(curr. Dim)){ curr. left = delete(p, curr. left, (curr. Dim + 1) % dimensions); } else { curr. right= delete(p, curr. right, (curr. Dim + 1) % dimensions); } return curr; } Again, depending on your design, this might be able to be copied verbatim in your project!
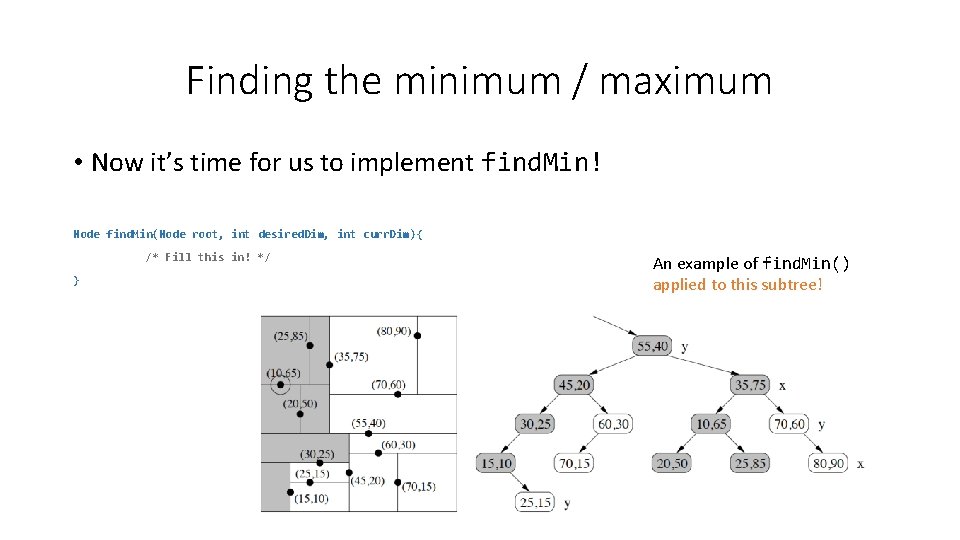
Finding the minimum / maximum • Now it’s time for us to implement find. Min! Node find. Min(Node root, int desired. Dim, int curr. Dim){ /* Fill this in! */ } An example of find. Min() applied to this subtree!
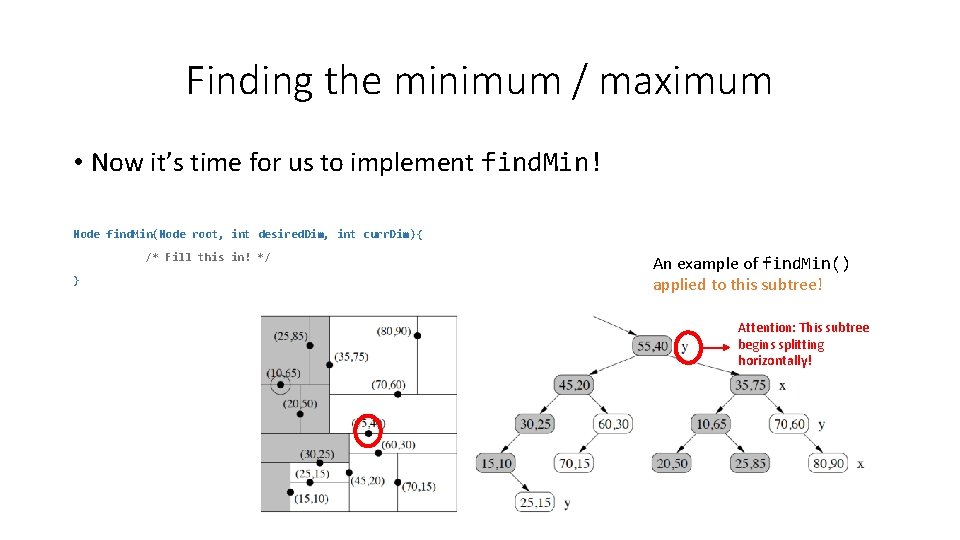
Finding the minimum / maximum • Now it’s time for us to implement find. Min! Node find. Min(Node root, int desired. Dim, int curr. Dim){ /* Fill this in! */ } An example of find. Min() applied to this subtree! Attention: This subtree begins splitting horizontally!

Finding the minimum / maximum • Now it’s time for us to implement find. Min! • We assume a method min() with 4 arguments that returns the node with the minimum value of the provided dimension. Node find. Min(Node root, int desired. Dim, int curr. Dim){ if(root == null) return null; else if(curr. Dim == desired. Dim){ if(root. left == null) return root; else return find. Min(root. left, desired. Dim, (curr. Dim + 1) % dimensions); } else { return min(root, find. Min(root. left, desired. Dim, (curr. Dim + 1) % dimensions), find. Min(root. right, desired. Dim, (curr. Dim + 1) % dimensions ), desired. Dim); }

Finding the minimum / maximum • Now it’s time for us to implement find. Min! • We assume a method min() with 4 arguments that returns the node with the minimum value of the provided dimension. Node find. Min(Node root, int desired. Dim, int curr. Dim){ if(root == null) return null; else if(curr. Dim == desired. Dim){ if(root. left == null) return root; else return find. Min(root. left, desired. Dim, (curr. Dim + 1) % dimensions); } else { return min(root, find. Min(root. left, desired. Dim, (curr. Dim + 1) % dimensions), find. Min(root. right, desired. Dim, (curr. Dim + 1) % dimensions ), desired. Dim); } Once again, depending on your modelling, this might be able to be copied verbatim!

Search • Search works in the exact same way as insertion. • Since it’s not interesting in terms of code, let’s see how efficient we expect it to be…
Analyzing KDTree efficiency • Something Else
Analyzing KDTree efficiency • Uniform distribution of keys implied! Something Else

Range •

Range • Convention #1: Our ranges will be closed (in the project too!) Convention #2: We do not report the “anchor” point itself (also in the project).

Range Query examples •
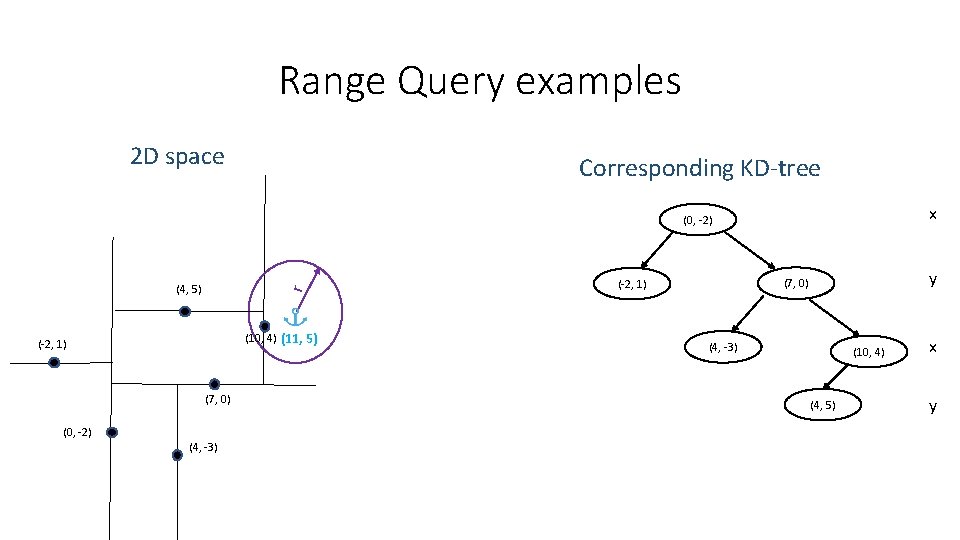
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) (10, 4) (4, 5) x y
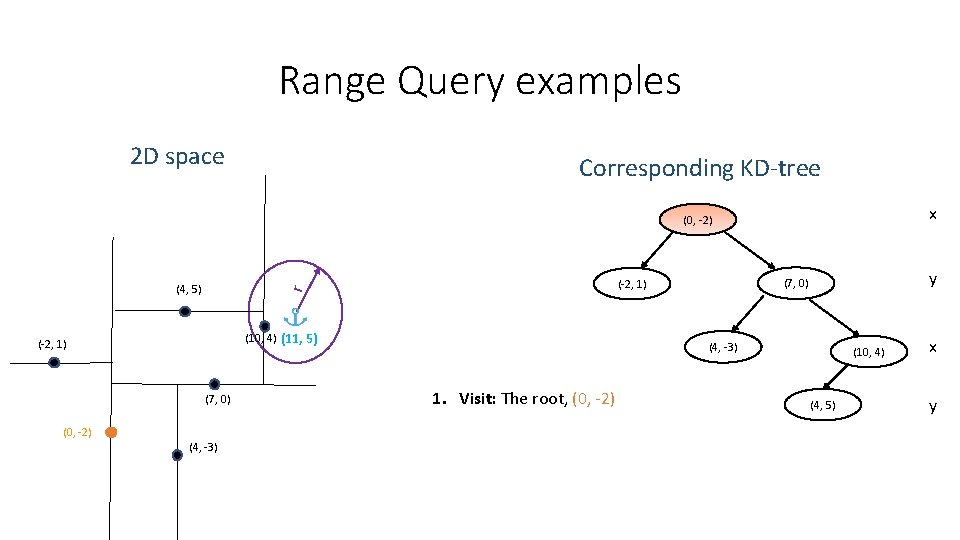
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Visit: The root, (0, -2) (10, 4) (4, 5) x y
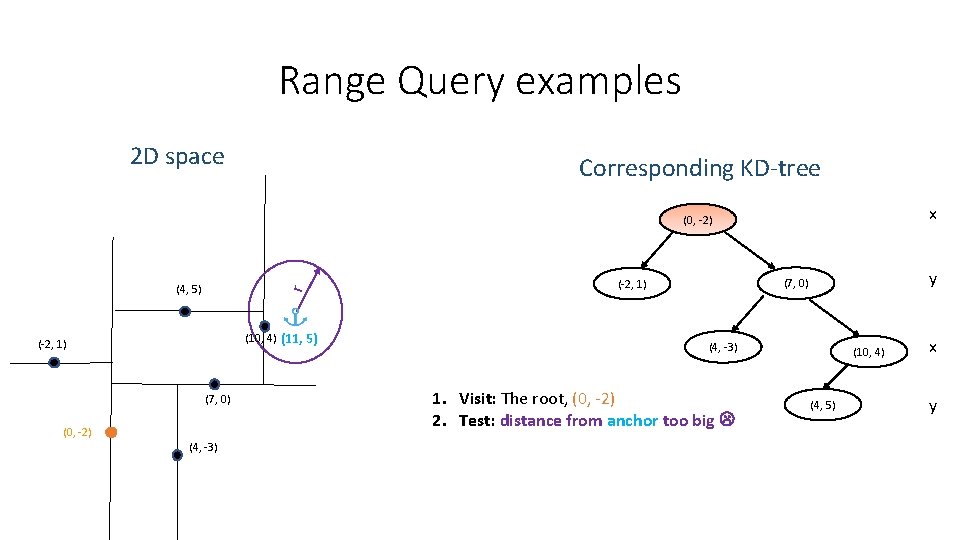
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: The root, (0, -2) 2. Test: distance from anchor too big (10, 4) (4, 5) x y
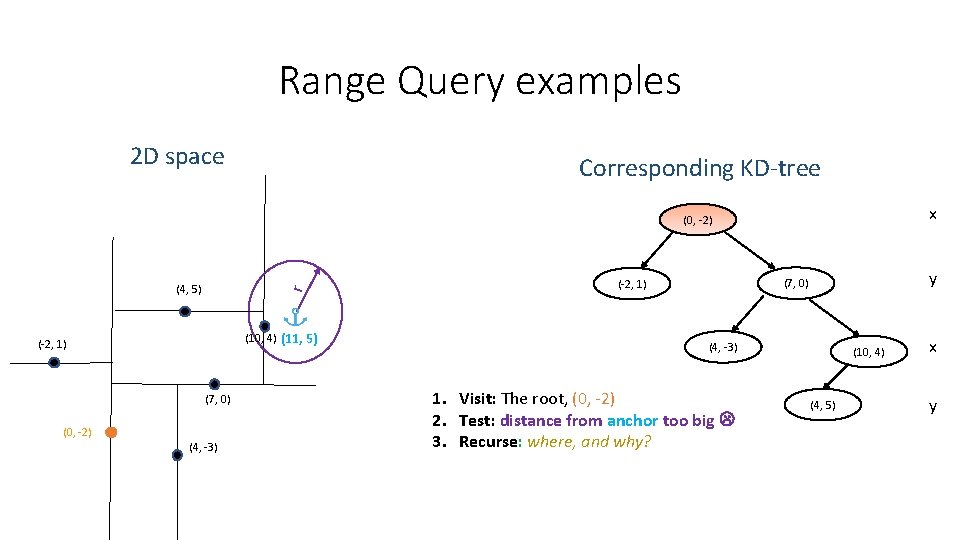
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: The root, (0, -2) 2. Test: distance from anchor too big 3. Recurse: where, and why? (10, 4) (4, 5) x y
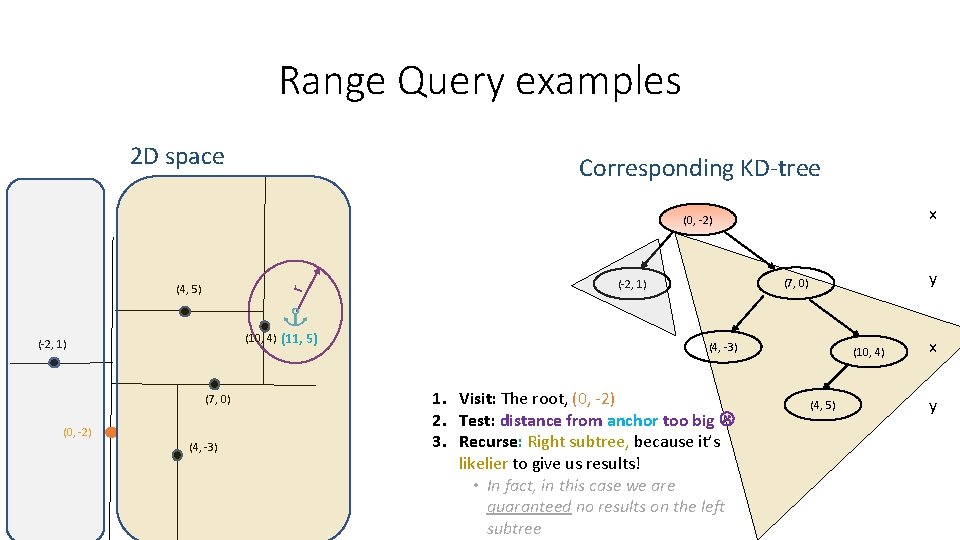
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: The root, (0, -2) 2. Test: distance from anchor too big 3. Recurse: Right subtree, because it’s likelier to give us results! • In fact, in this case we are guaranteed no results on the left subtree (10, 4) (4, 5) x y
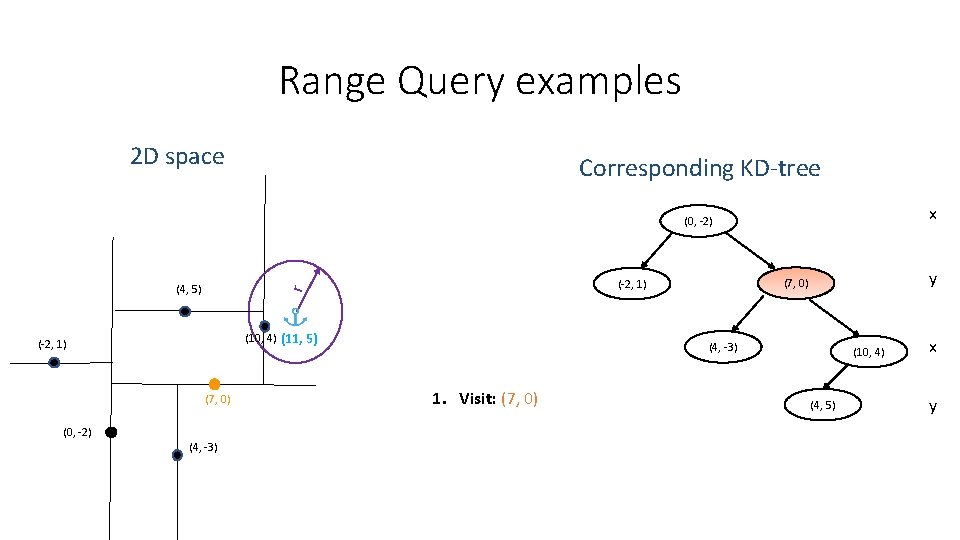
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Visit: (7, 0) (10, 4) (4, 5) x y
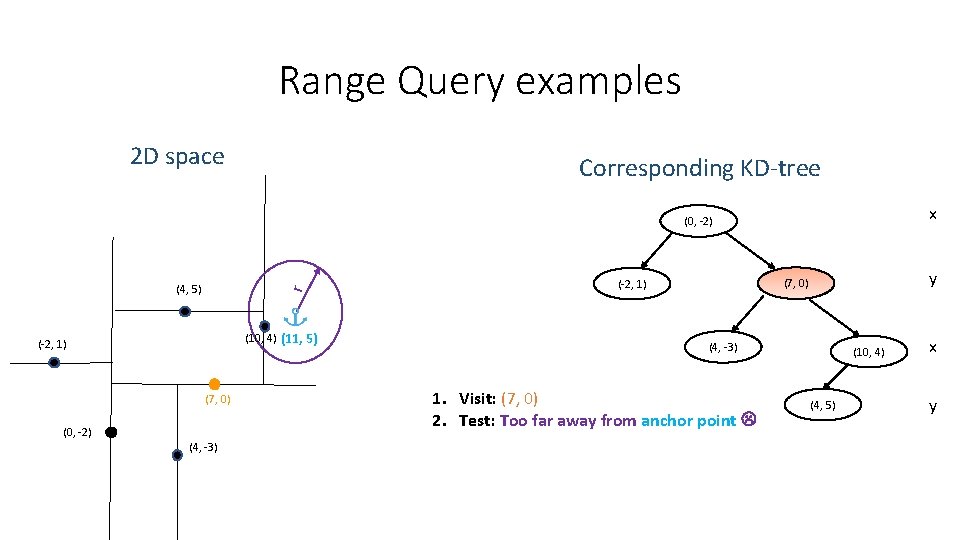
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: (7, 0) 2. Test: Too far away from anchor point (10, 4) (4, 5) x y
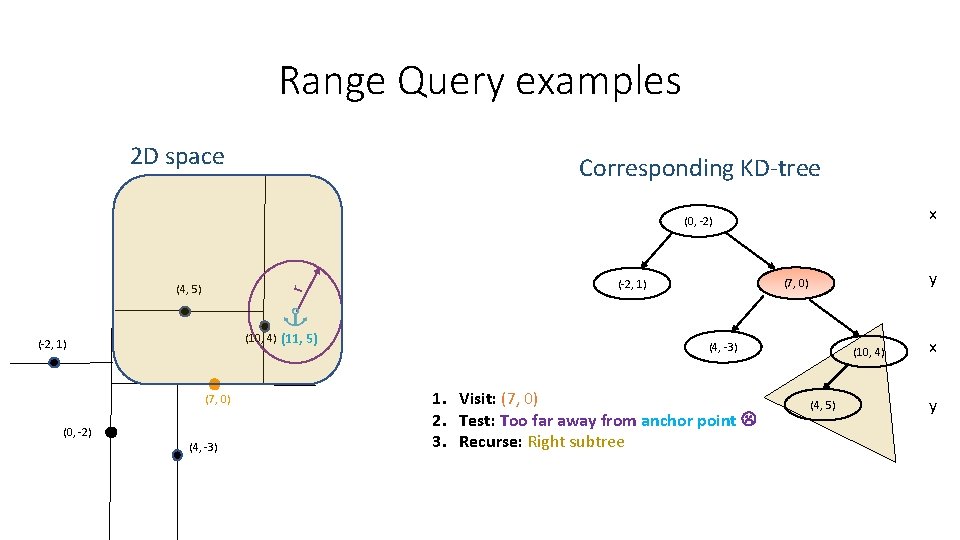
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: (7, 0) 2. Test: Too far away from anchor point 3. Recurse: Right subtree (10, 4) (4, 5) x y
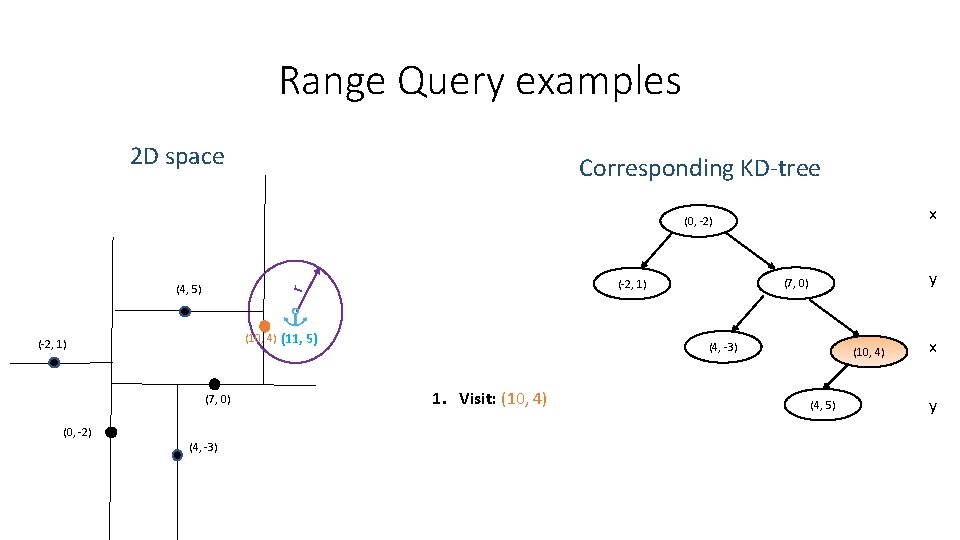
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Visit: (10, 4) (4, 5) x y
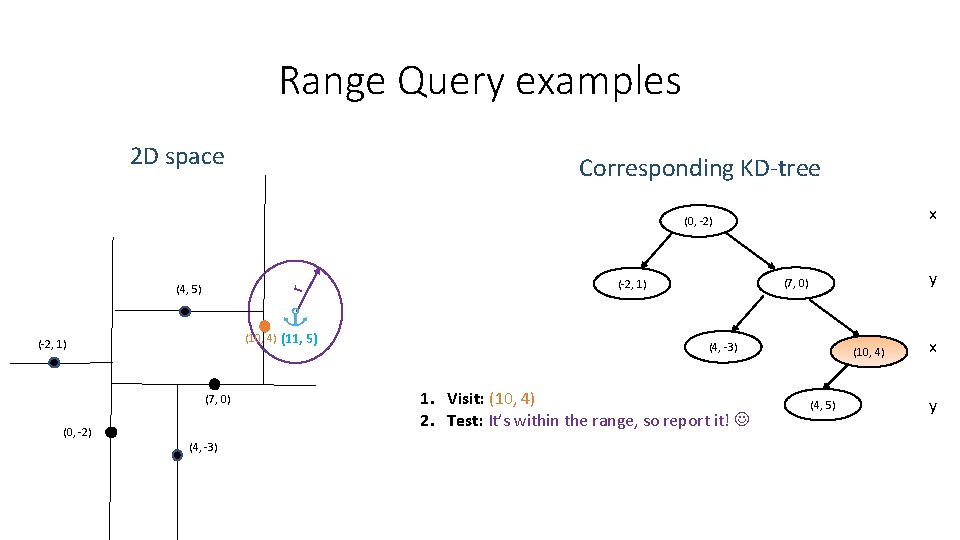
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: (10, 4) 2. Test: It’s within the range, so report it! (10, 4) (4, 5) x y
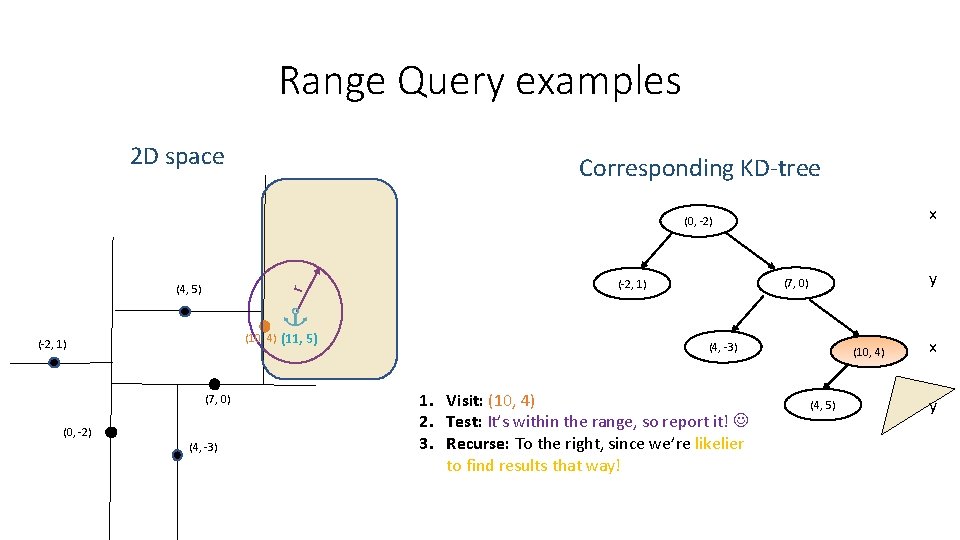
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: (10, 4) 2. Test: It’s within the range, so report it! 3. Recurse: To the right, since we’re likelier to find results that way! (10, 4) (4, 5) x y
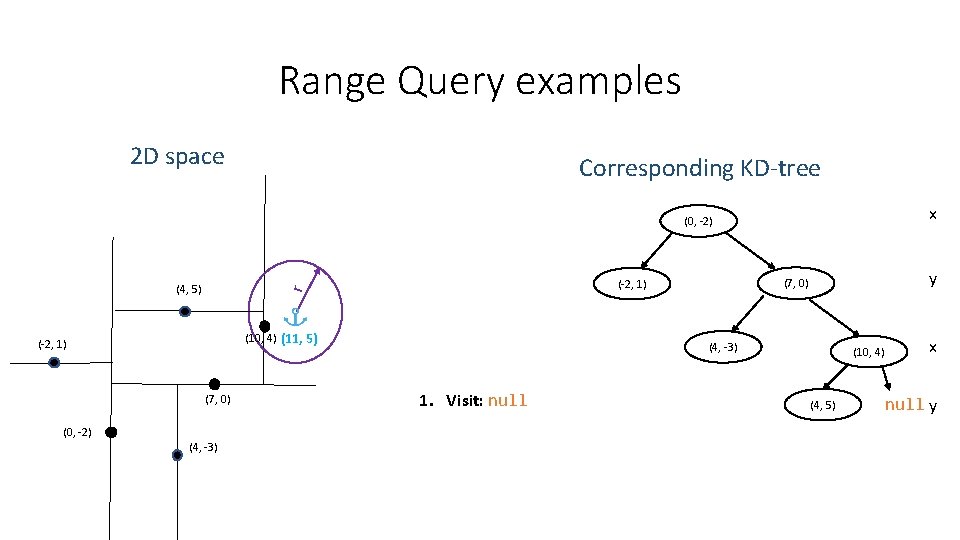
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Visit: null (10, 4) (4, 5) x null y
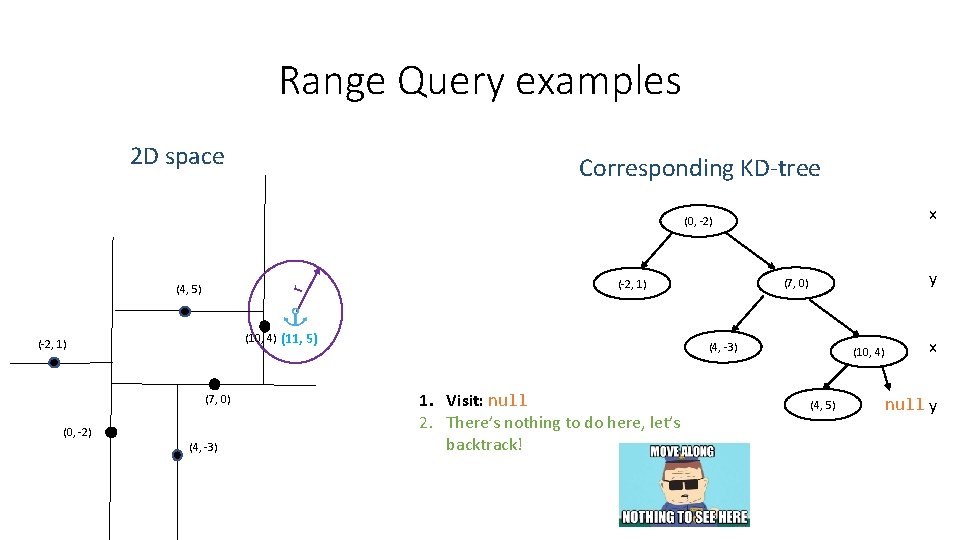
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: null 2. There’s nothing to do here, let’s backtrack! (10, 4) (4, 5) x null y
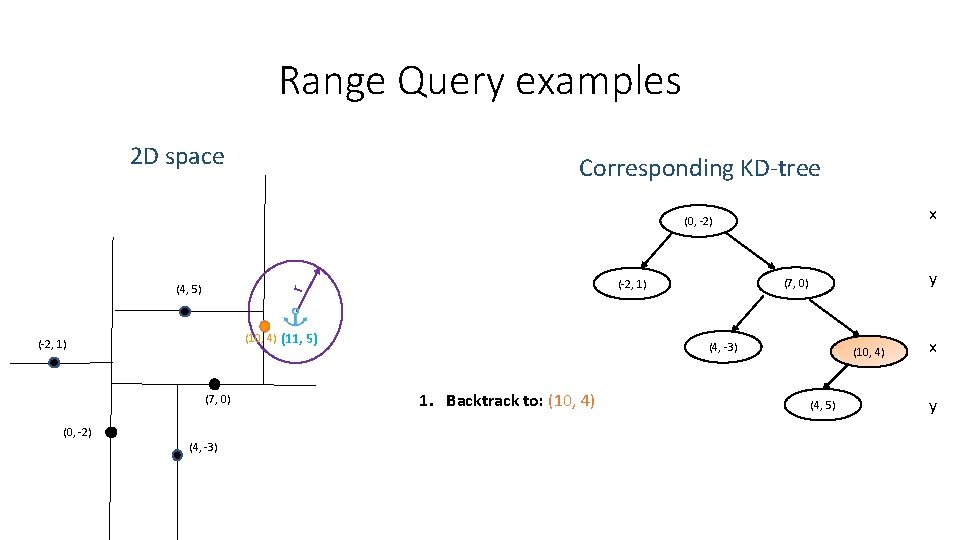
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Backtrack to: (10, 4) (4, 5) x y
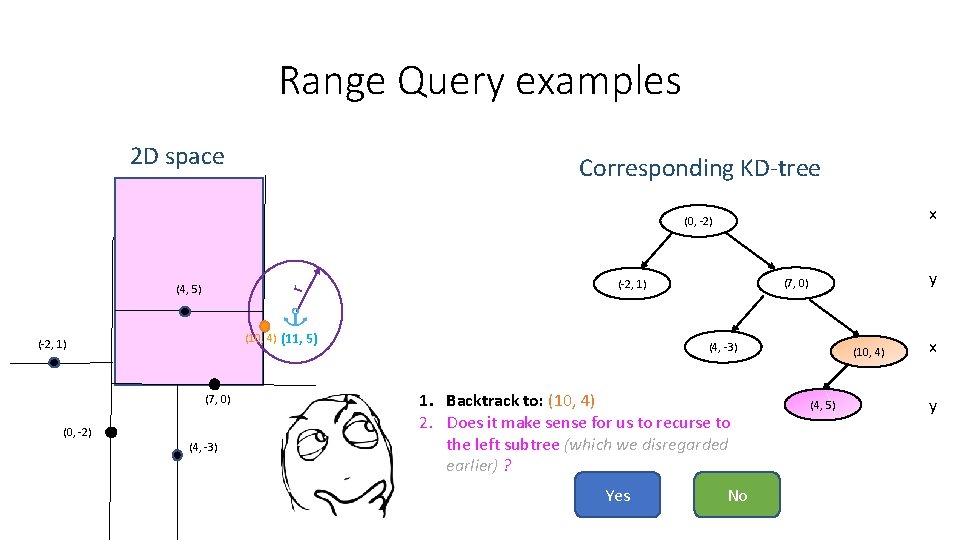
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Backtrack to: (10, 4) 2. Does it make sense for us to recurse to the left subtree (which we disregarded earlier) ? Yes No (10, 4) (4, 5) x y
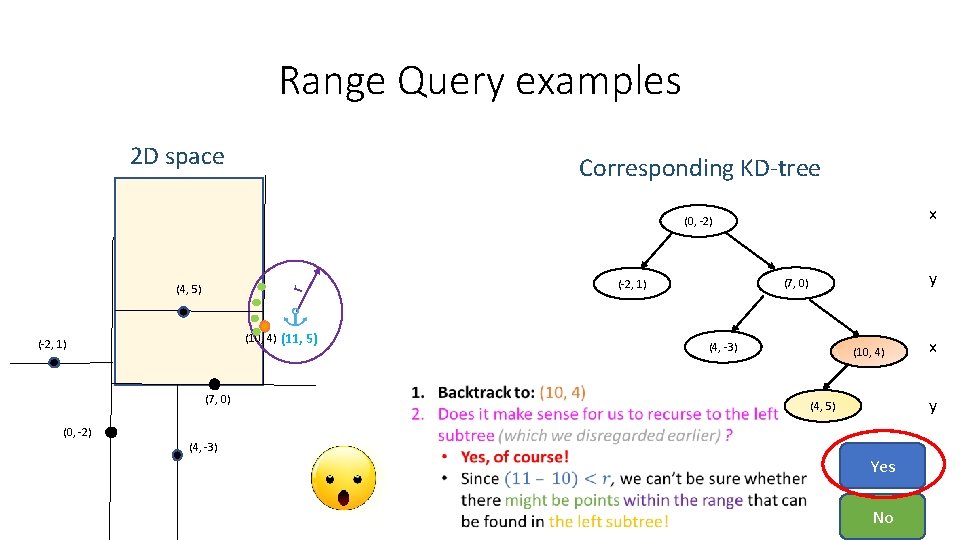
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) y (7, 0) (-2, 1) r (4, 5) (4, -3) (10, 4) x y (4, 5) (0, -2) (4, -3) Yes No
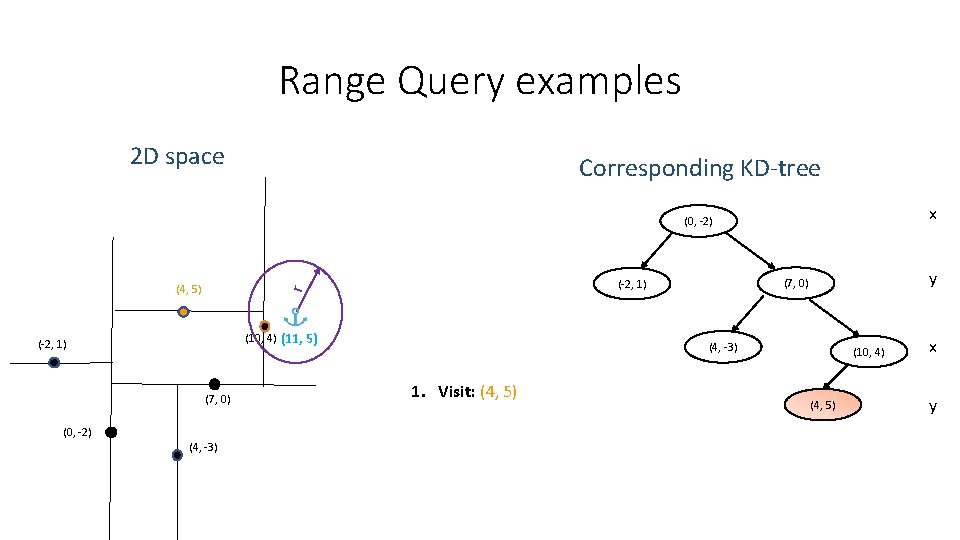
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Visit: (4, 5) (10, 4) (4, 5) x y
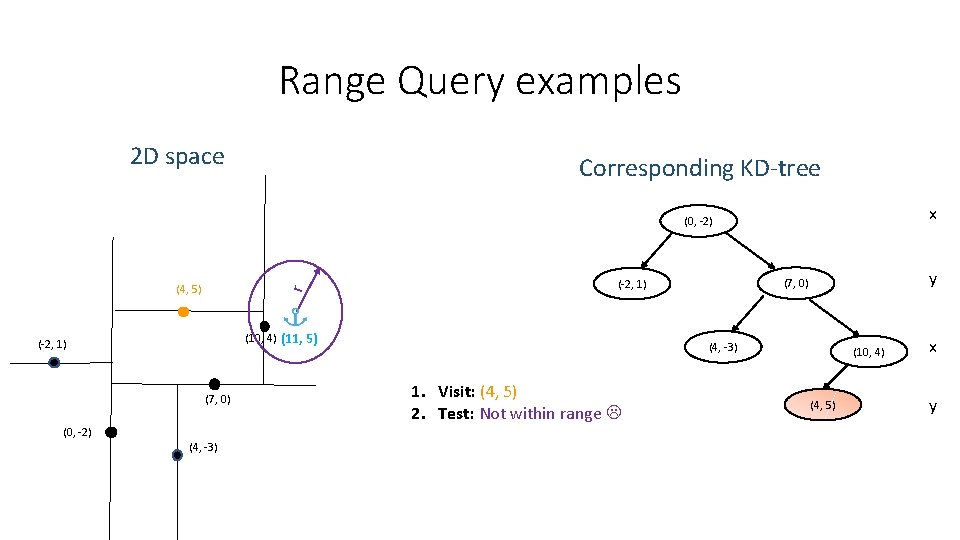
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, -3) 1. Visit: (4, 5) 2. Test: Not within range (10, 4) (4, 5) x y
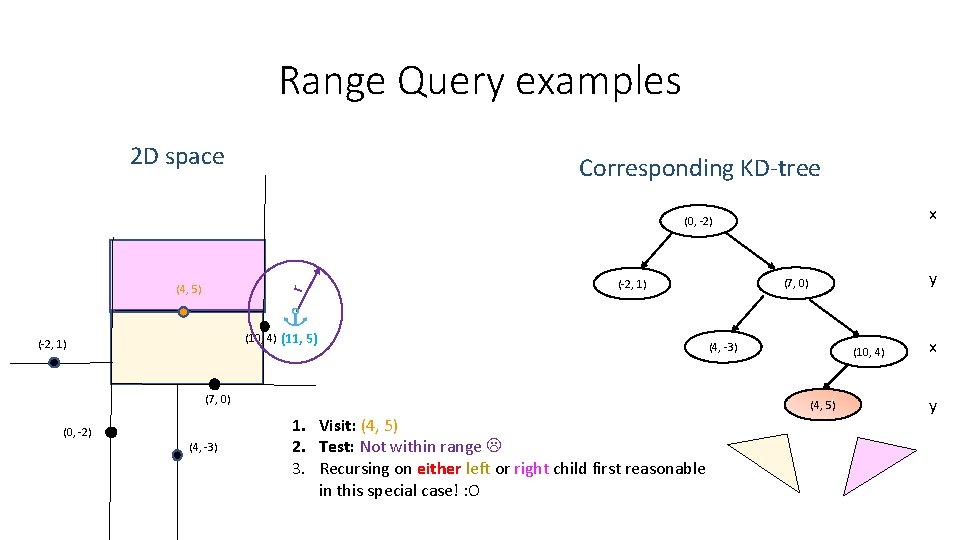
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (4, -3) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (10, 4) (4, 5) 1. Visit: (4, 5) 2. Test: Not within range 3. Recursing on either left or right child first reasonable in this special case! : O x y
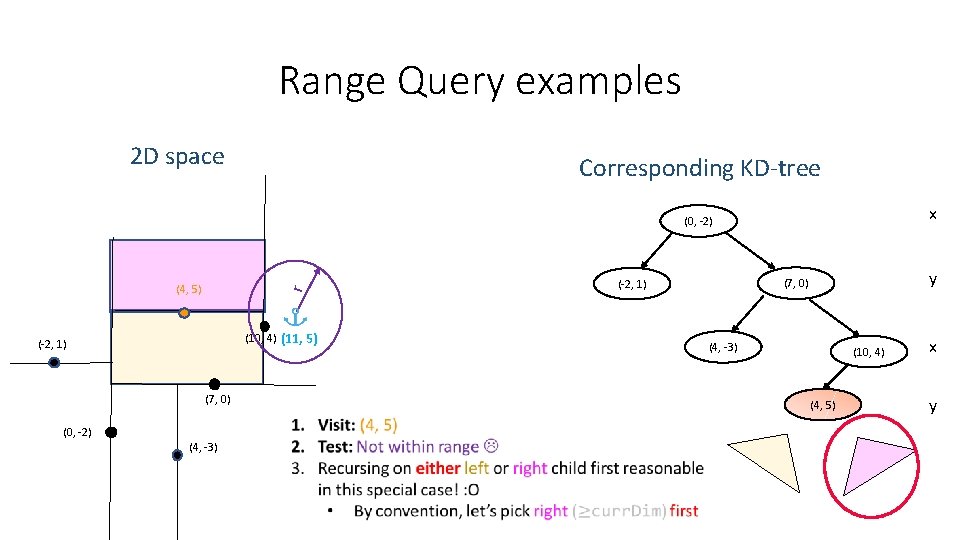
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (7, 0) (4, -3) (10, 4) (4, 5) (0, -2) y (7, 0) (-2, 1) x y
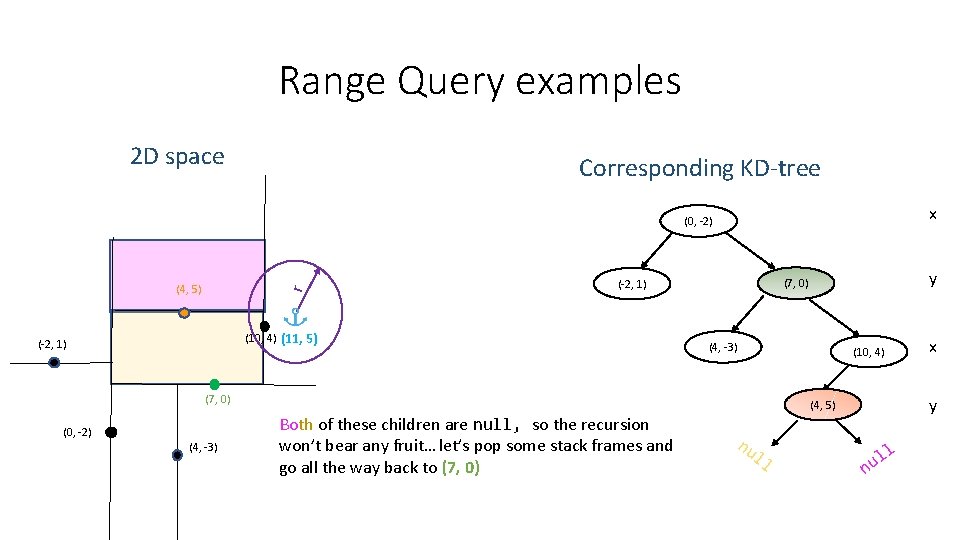
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (4, -3) (10, 4) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) y (4, 5) Both of these children are null, so the recursion won’t bear any fruit… let’s pop some stack frames and go all the way back to (7, 0) nu ll x ll u n
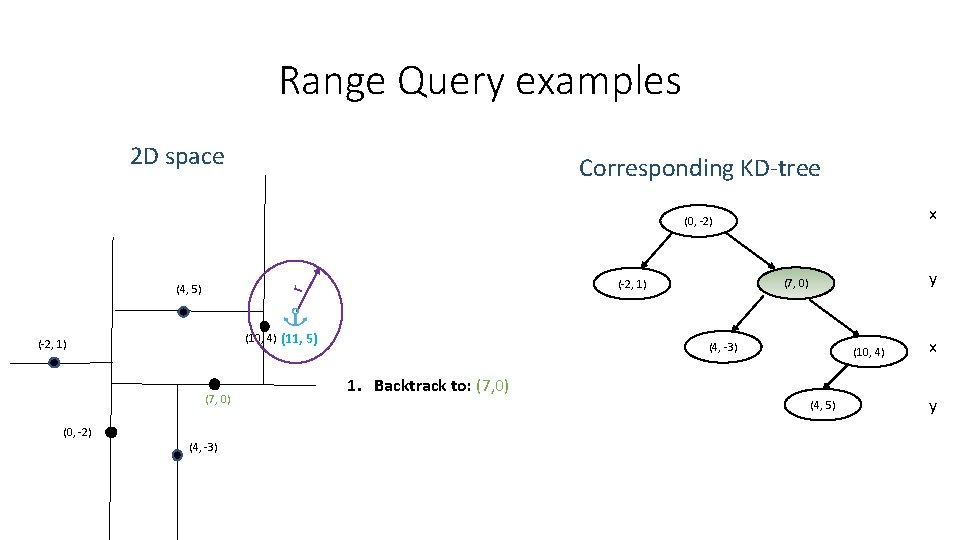
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) r (4, 5) (4, -3) (10, 4) 1. Backtrack to: (7, 0) (4, 5) x y
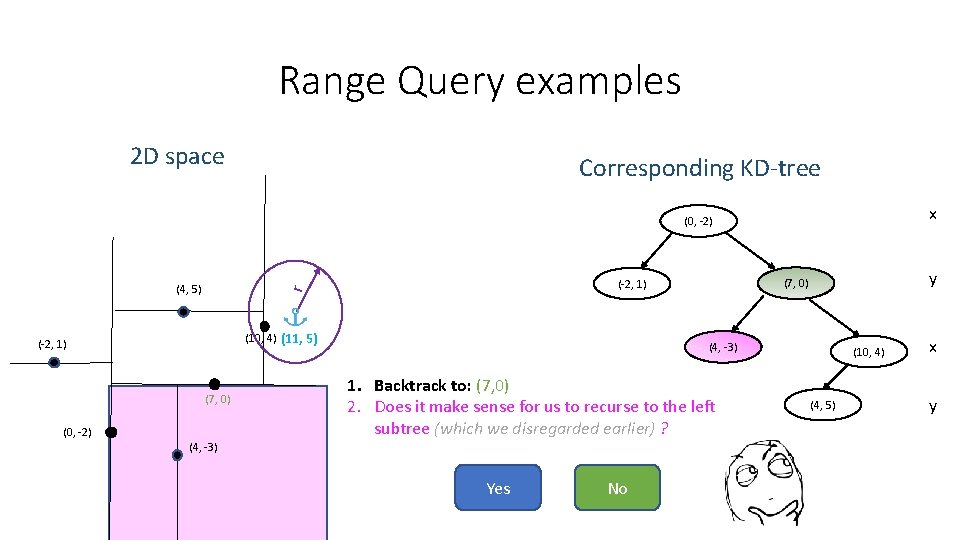
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (10, 4) (11, 5) (-2, 1) (7, 0) (0, -2) y (7, 0) (-2, 1) r (4, 5) (4, -3) 1. Backtrack to: (7, 0) 2. Does it make sense for us to recurse to the left subtree (which we disregarded earlier) ? (4, -3) Yes No (10, 4) (4, 5) x y
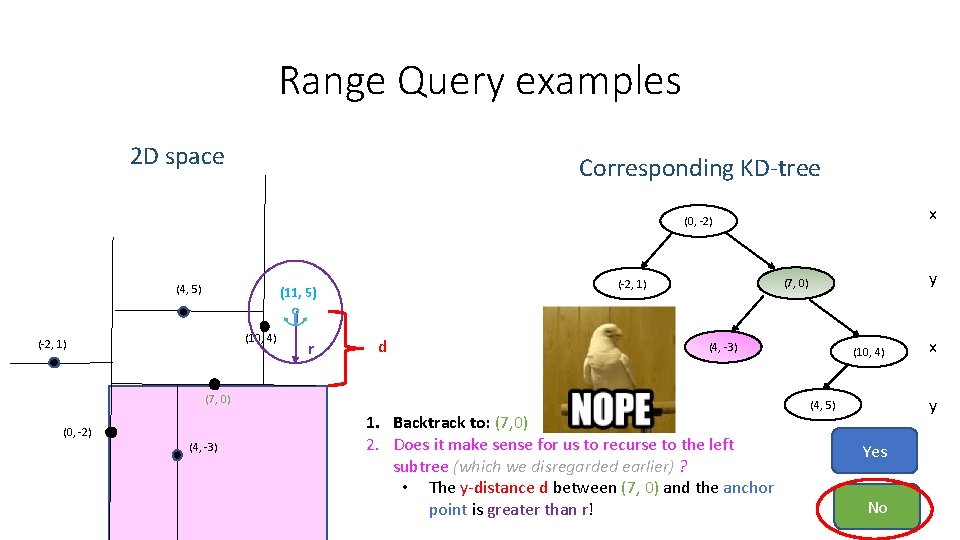
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (4, 5) (11, 5) (10, 4) (-2, 1) r d (4, -3) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) 1. Backtrack to: (7, 0) 2. Does it make sense for us to recurse to the left subtree (which we disregarded earlier) ? • The y-distance d between (7, 0) and the anchor point is greater than r! (10, 4) x y (4, 5) Yes No
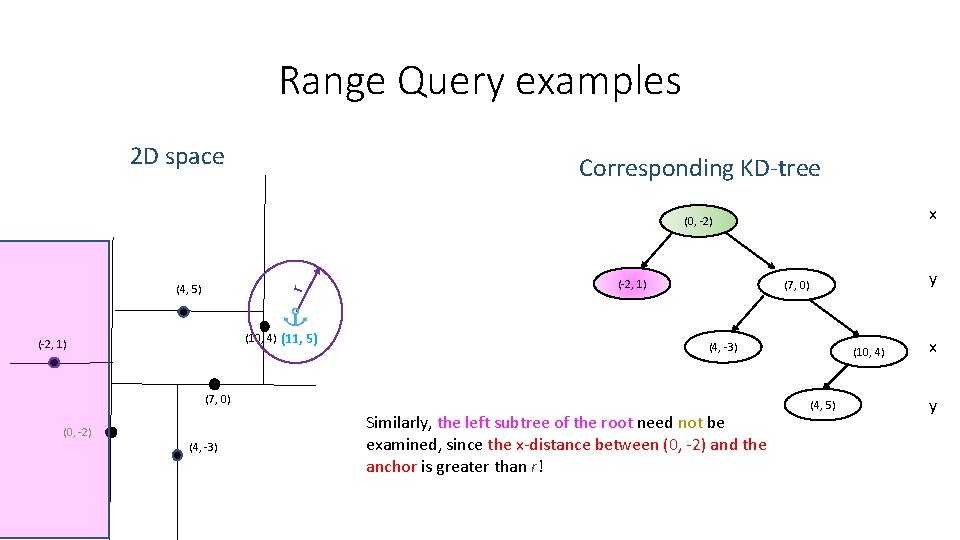
Range Query examples 2 D space Corresponding KD-tree x (0, -2) r (4, 5) (10, 4) (11, 5) (-2, 1) (4, -3) (7, 0) (0, -2) (4, -3) y (7, 0) Similarly, the left subtree of the root need not be examined, since the x-distance between (0, -2) and the anchor is greater than r! (10, 4) (4, 5) x y
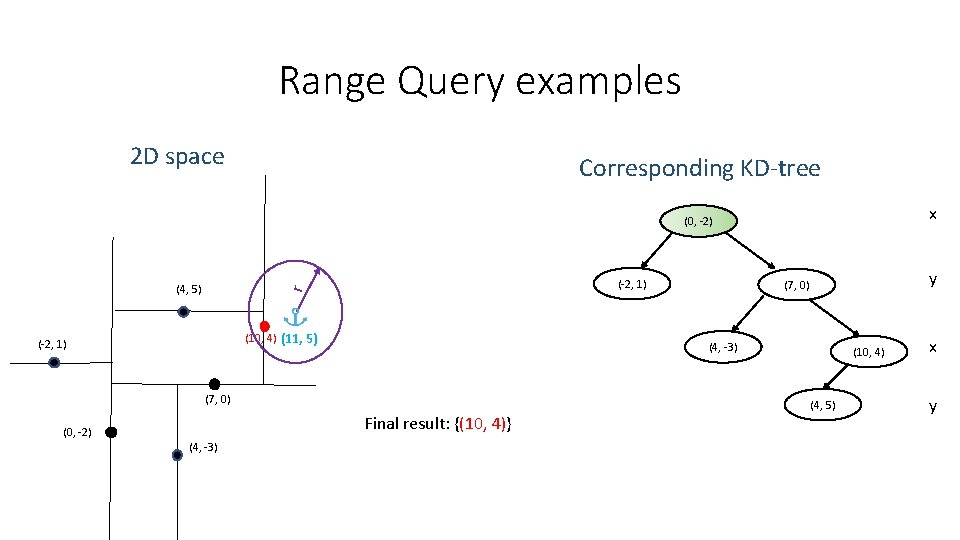
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (-2, 1) r (4, 5) (10, 4) (11, 5) (-2, 1) (4, -3) (7, 0) (4, -3) (10, 4) (4, 5) Final result: {(10, 4)} (0, -2) y (7, 0) x y
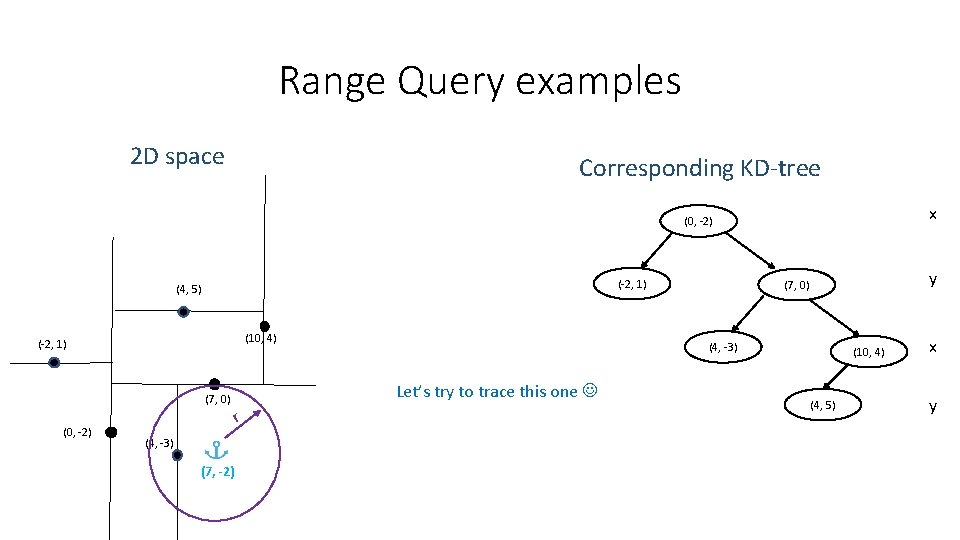
Range Query examples 2 D space Corresponding KD-tree x (0, -2) (-2, 1) (4, 5) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) (7, -2) (4, -3) Let’s try to trace this one r y (7, 0) (10, 4) (4, 5) x y
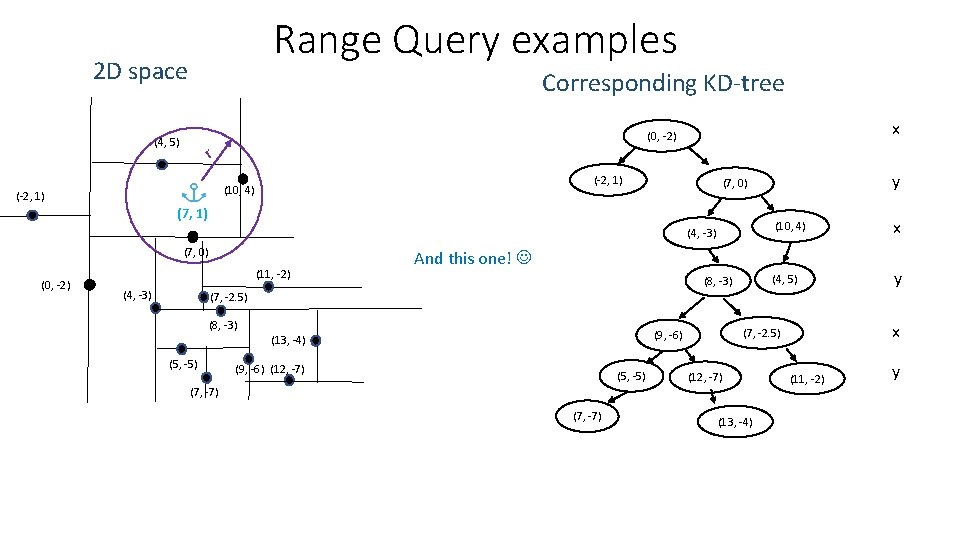
Range Query examples 2 D space Corresponding KD-tree (4, 5) r (-2, 1) (10, 4) (-2, 1) x (0, -2) (7, 1) (4, -3) (7, 0) (0, -2) (11, -2) (4, -3) y (7, 0) (10, 4) x (4, 5) y And this one! (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
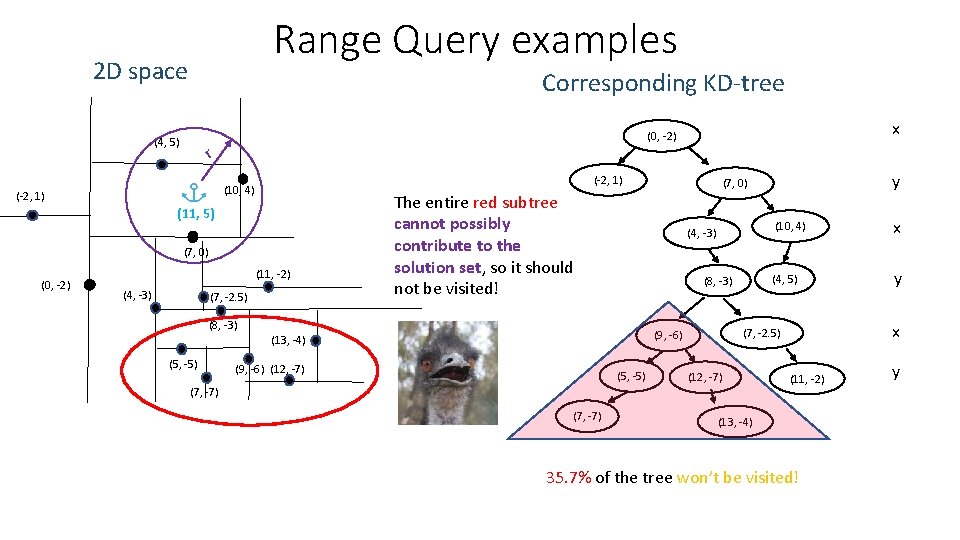
Range Query examples 2 D space Corresponding KD-tree (4, 5) r (-2, 1) (10, 4) (-2, 1) (11, 5) (7, 0) (0, -2) (11, -2) (4, -3) (7, -2. 5) (4, -3) (8, -3) (9, -6) (12, -7) (5, -5) (7, -7) (10, 4) x (4, 5) y x (7, -2. 5) (9, -6) (13, -4) y (7, 0) The entire red subtree cannot possibly contribute to the solution set, so it should not be visited! (8, -3) (5, -5) x (0, -2) (12, -7) (11, -2) (13, -4) 35. 7% of the tree won’t be visited! y

Take-home messages 1. As we go down the tree, we behave greedily, by traversing the subtree likeliest to give us answers. • This is important in an application that mutates a global collection of the answers but whose tree-traversing thread can die for whatever reason! 2. When we backtrack up the tree, we potentially prune away large portions of the dataset since we are guaranteed to not be able to improve upon our search! • A tree-like structure like a KD-Tree helps a ton with this! • For dense datasets, this slows down as we approach the point, and speeds up as we get away from it!

Nearest neighbor •

Nearest neighbor • An even number An odd number A prime number A Mersenne Prime number

Nearest neighbor • An even number An odd number A prime number A Mersenne Prime number To avoid ties that you’d have to flip a coin for!

Nearest neighbor: idea •

Nearest neighbor: idea •

Nearest neighbor: idea •
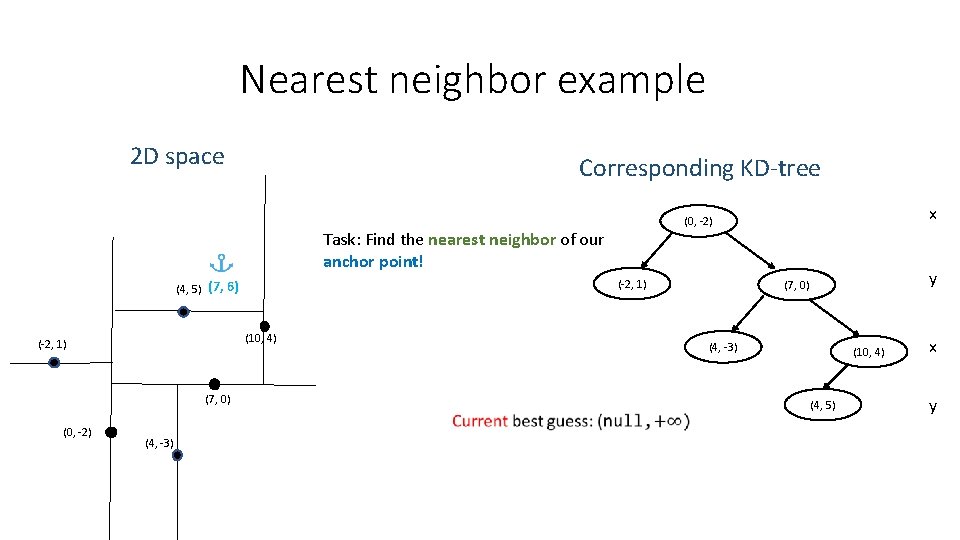
Nearest neighbor example 2 D space Corresponding KD-tree Task: Find the nearest neighbor of our anchor point! (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (4, -3) y (7, 0) (4, -3) (7, 0) (0, -2) x (0, -2) (10, 4) (4, 5) x y
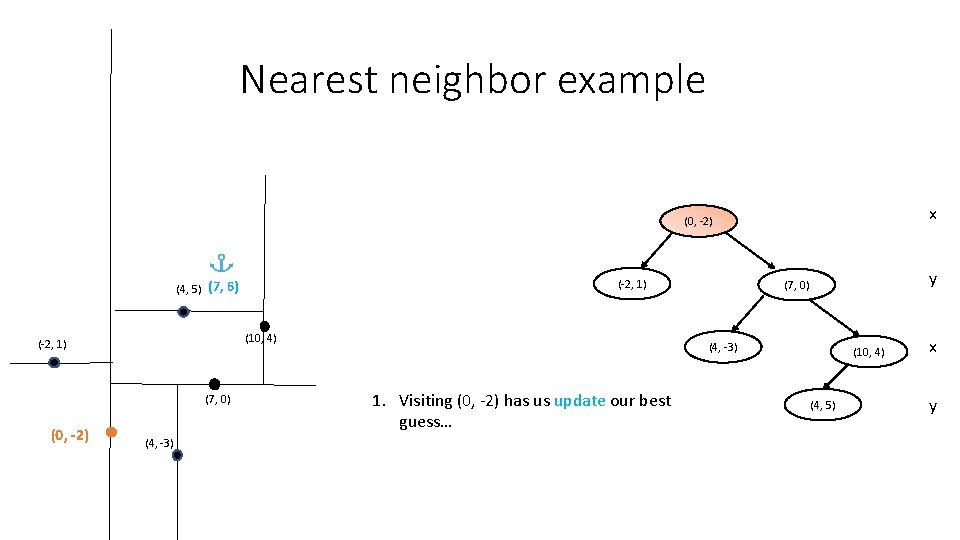
Nearest neighbor example x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (4, -3) 1. Visiting (0, -2) has us update our best guess… (10, 4) (4, 5) x y
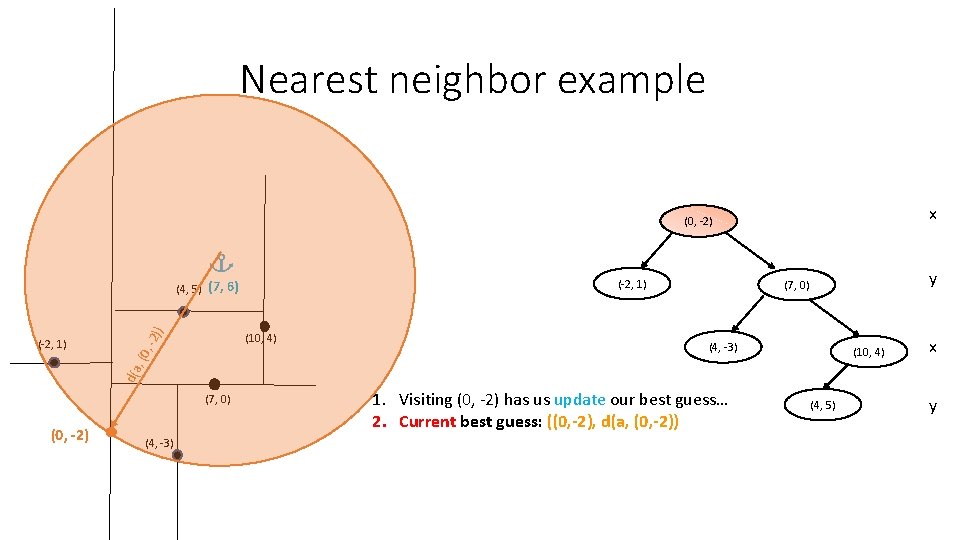
Nearest neighbor example x (0, -2) (-2, 1) , -2 (10, 4) y (7, 0) (4, -3) (10, 4) x d(a , (0 (-2, 1) )) (4, 5) (7, 6) (7, 0) (0, -2) (4, -3) 1. Visiting (0, -2) has us update our best guess… 2. Current best guess: ((0, -2), d(a, (0, -2)) (4, 5) y
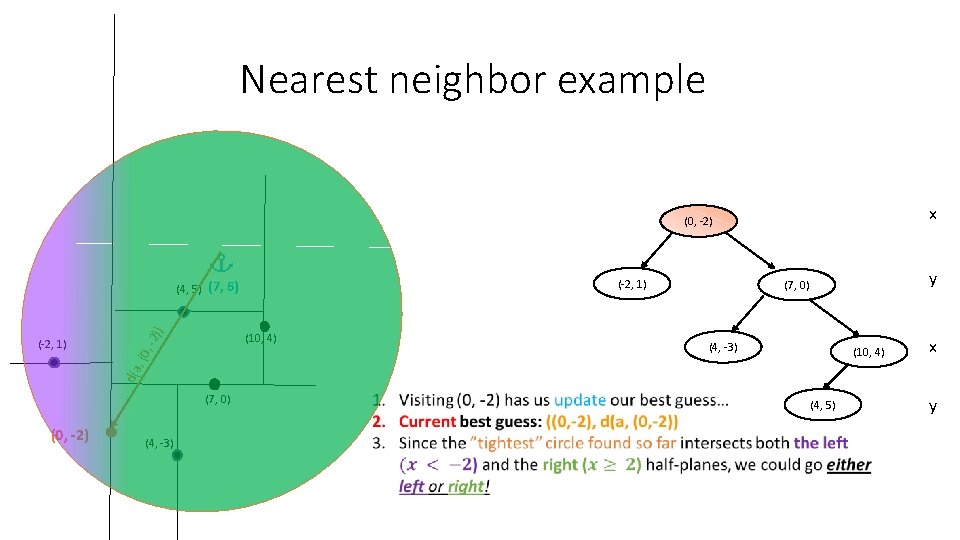
Nearest neighbor example x (0, -2) (-2, 1) , -2 (10, 4) y (7, 0) (4, -3) (10, 4) x d(a , (0 (-2, 1) )) (4, 5) (7, 6) (7, 0) (0, -2) (4, -3) (4, 5) y
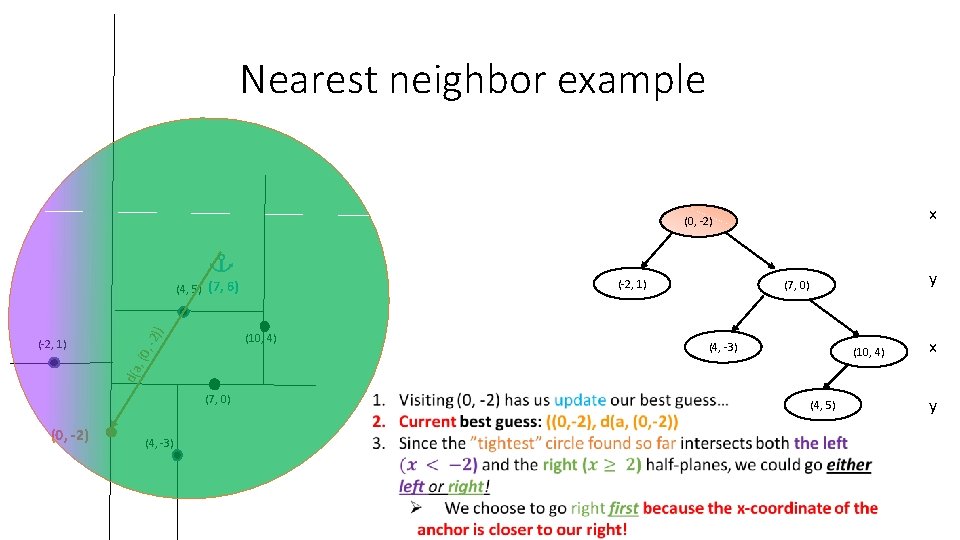
Nearest neighbor example x (0, -2) (-2, 1) , -2 (10, 4) y (7, 0) (4, -3) (10, 4) x d(a , (0 (-2, 1) )) (4, 5) (7, 6) (7, 0) (0, -2) (4, -3) (4, 5) y
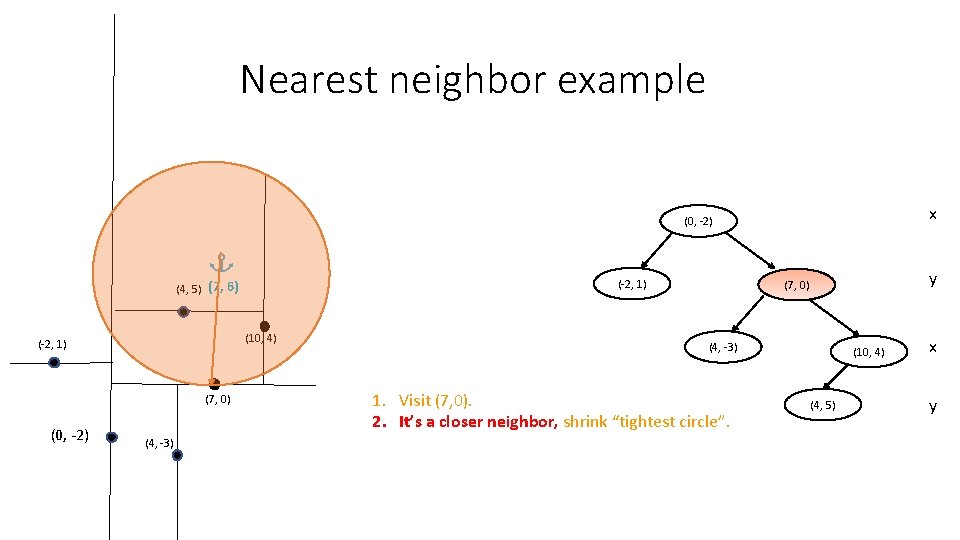
Nearest neighbor example x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (4, -3) 1. Visit (7, 0). 2. It’s a closer neighbor, shrink “tightest circle”. (10, 4) (4, 5) x y
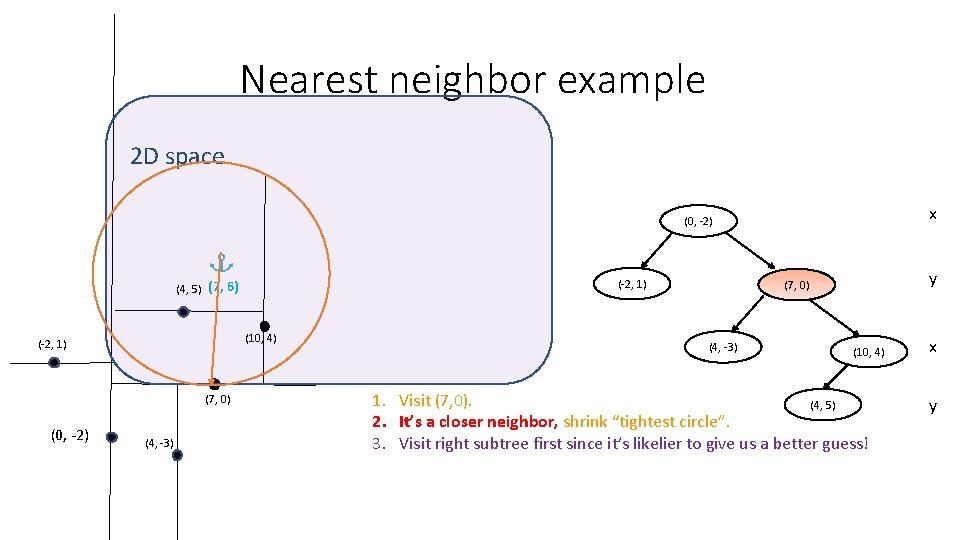
Nearest neighbor example 2 D space x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (4, -3) (10, 4) 1. Visit (7, 0). (4, 5) 2. It’s a closer neighbor, shrink “tightest circle”. 3. Visit right subtree first since it’s likelier to give us a better guess! x y
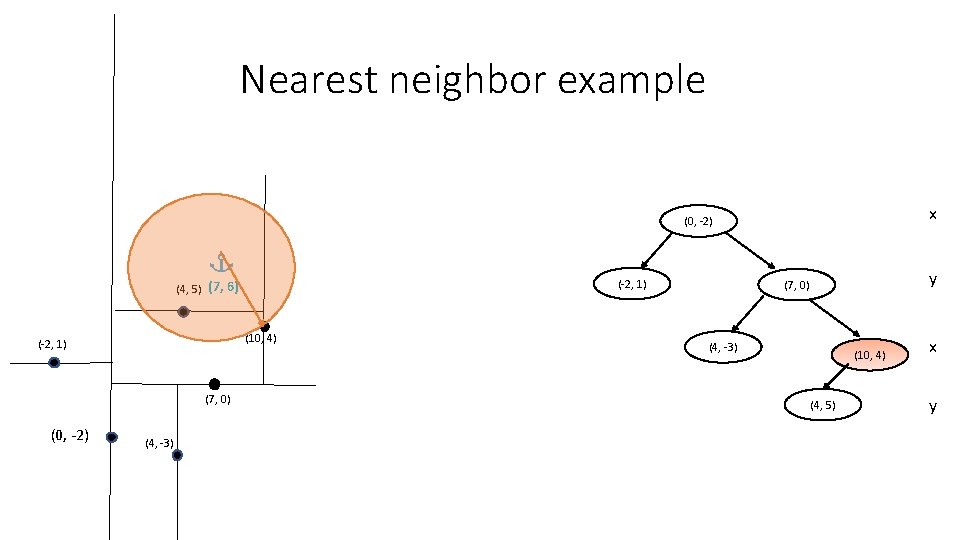
Nearest neighbor example x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (4, -3) (10, 4) (4, 5) x y
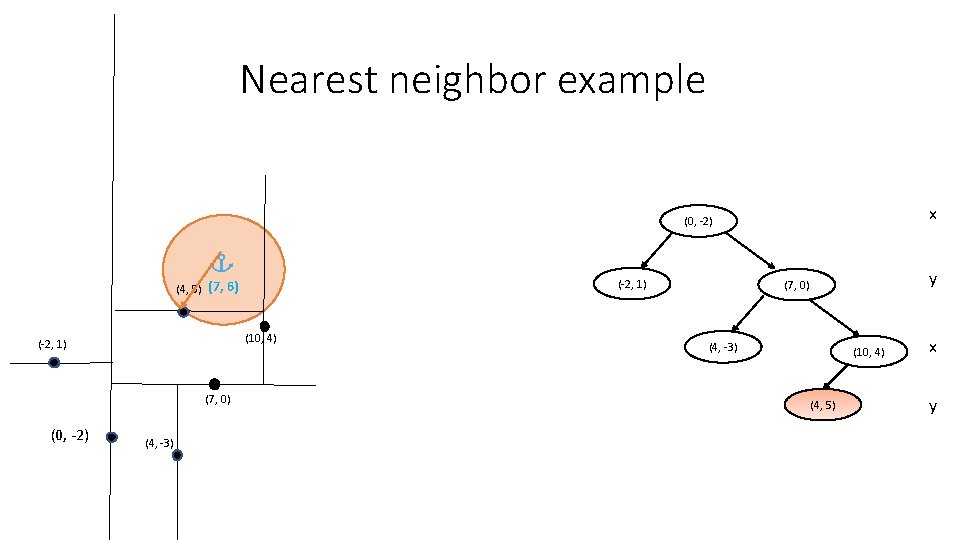
Nearest neighbor example x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (4, -3) (10, 4) (4, 5) x y
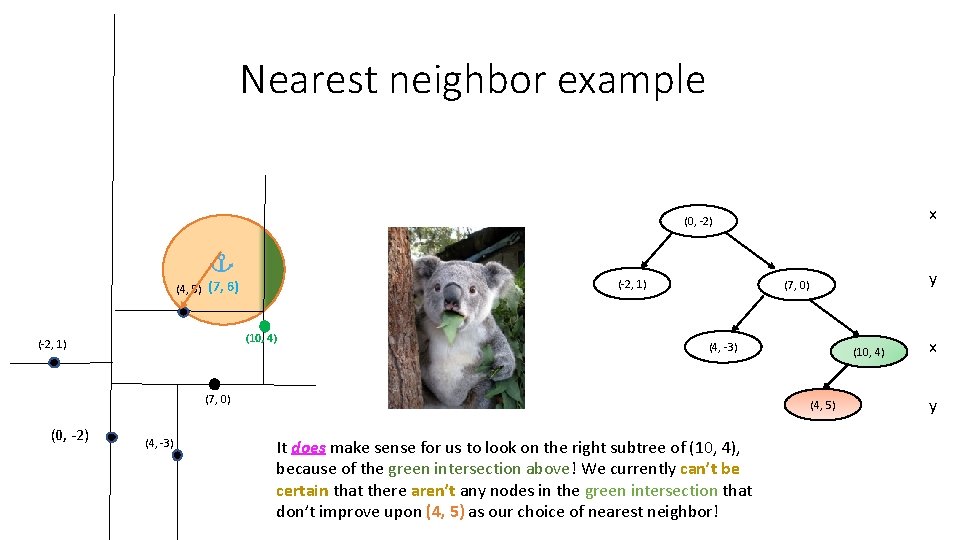
Nearest neighbor example x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (4, -3) (7, 0) (0, -2) (4, -3) y (7, 0) (10, 4) (4, 5) It does make sense for us to look on the right subtree of (10, 4), because of the green intersection above! We currently can’t be certain that there aren’t any nodes in the green intersection that don’t improve upon (4, 5) as our choice of nearest neighbor! x y
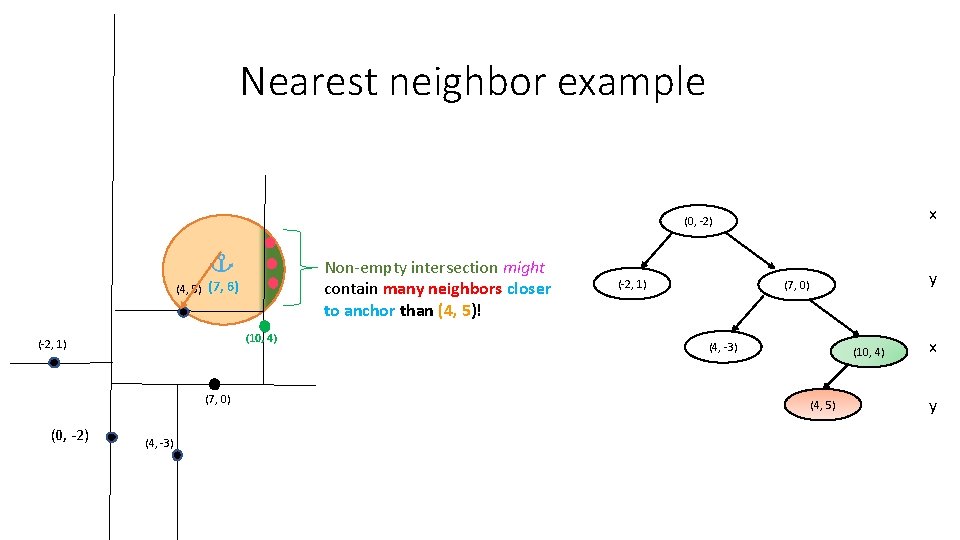
Nearest neighbor example x (0, -2) Non-empty intersection might contain many neighbors closer to anchor than (4, 5)! (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) (-2, 1) y (7, 0) (4, -3) (10, 4) (4, 5) x y
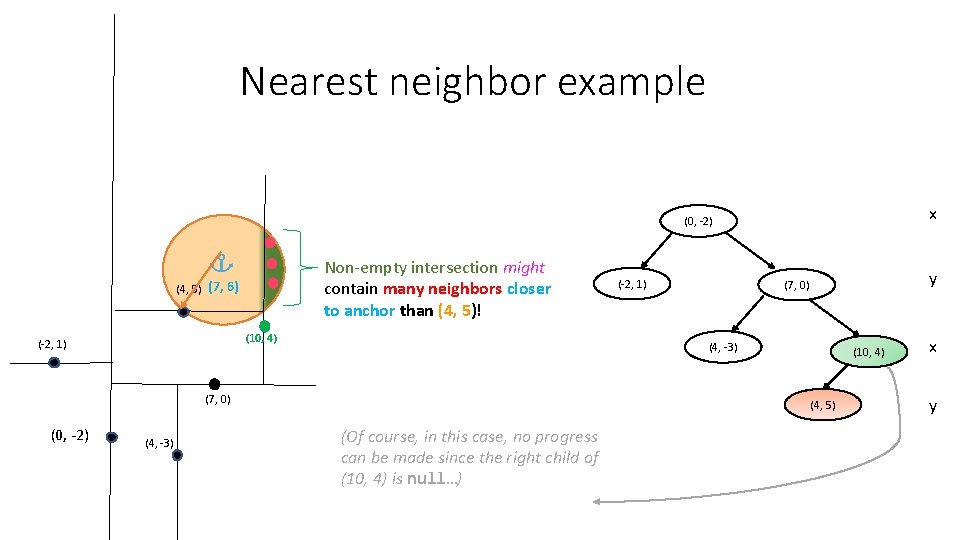
Nearest neighbor example x (0, -2) Non-empty intersection might contain many neighbors closer to anchor than (4, 5)! (4, 5) (7, 6) (10, 4) (-2, 1) (4, -3) y (7, 0) (4, -3) (7, 0) (0, -2) (-2, 1) (10, 4) (4, 5) (Of course, in this case, no progress can be made since the right child of (10, 4) is null…) x y
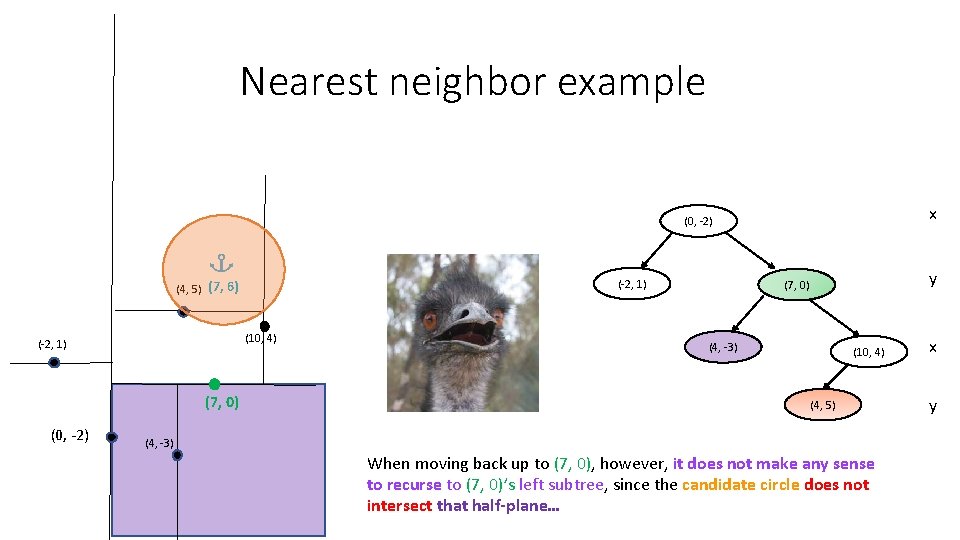
Nearest neighbor example x (0, -2) (-2, 1) (4, 5) (7, 6) (10, 4) (-2, 1) (7, 0) (0, -2) y (7, 0) (4, -3) (10, 4) (4, 5) (4, -3) When moving back up to (7, 0), however, it does not make any sense to recurse to (7, 0)’s left subtree, since the candidate circle does not intersect that half-plane… x y
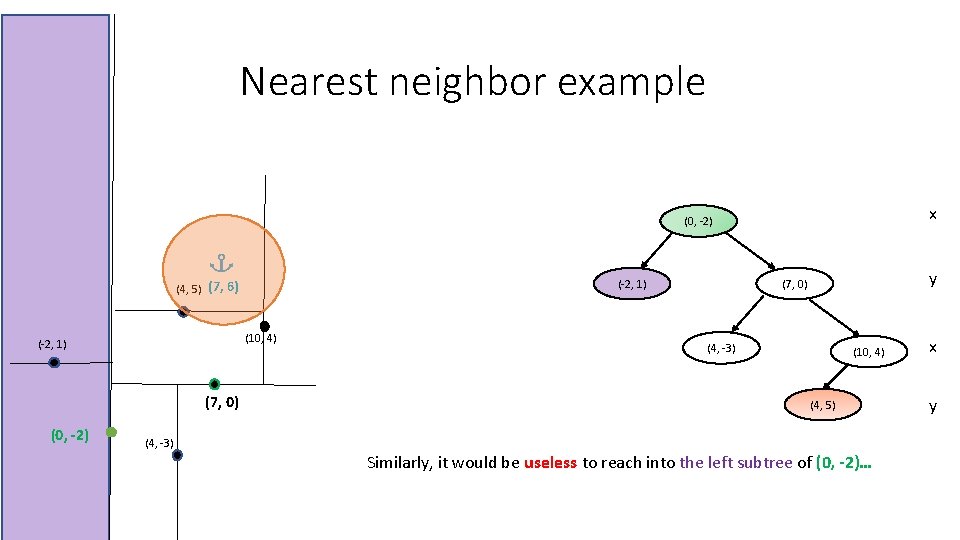
Nearest neighbor example x (0, -2) (10, 4) (-2, 1) (7, 0) (0, -2) y (7, 0) (-2, 1) (4, 5) (7, 6) (4, -3) (10, 4) (4, 5) (4, -3) Similarly, it would be useless to reach into the left subtree of (0, -2)… x y
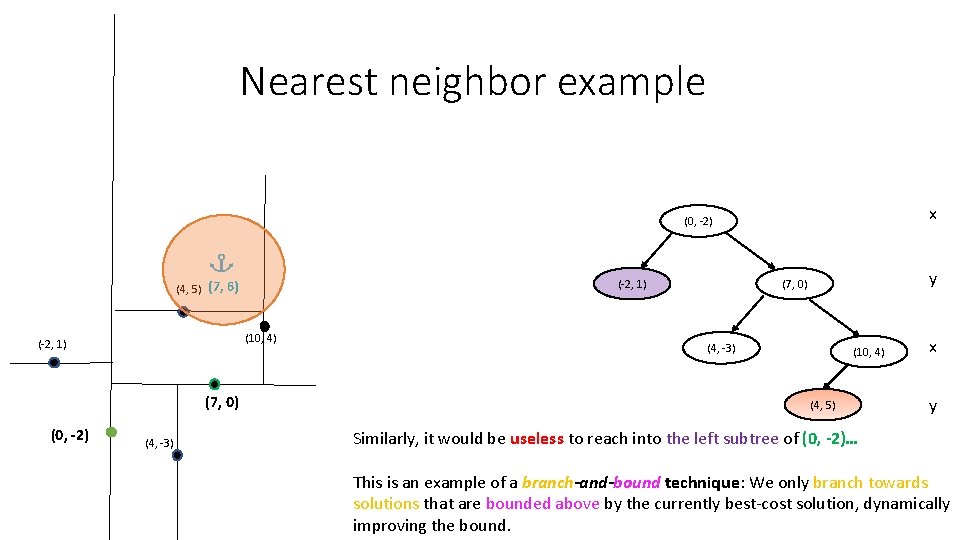
Nearest neighbor example x (0, -2) (10, 4) (-2, 1) (7, 0) (0, -2) (4, -3) y (7, 0) (-2, 1) (4, 5) (7, 6) (4, -3) (10, 4) (4, 5) x y Similarly, it would be useless to reach into the left subtree of (0, -2)… This is an example of a branch-and-bound technique: We only branch towards solutions that are bounded above by the currently best-cost solution, dynamically improving the bound.



• Linked List A balanced binary tree A stack Something else (what? )

• A priority queue! Linked List A balanced binary tree A stack Something else (what? )

• And not just any priority queue…. Linked List A balanced binary tree A stack Something else (what? )

Bounded priority queues • We assume any implementation of a Priority Queue. • (But really, you should probably use binary heaps for these kinds of problems). • A Bounded Priority Queue (hereafter BPQ) behaves like any PQ, except for the following details:

Bounded priority queues •

Bounded priority queues •

Bounded priority queues •

Bounded priority queues •

Bounded priority queues •

Bounded priority queues •
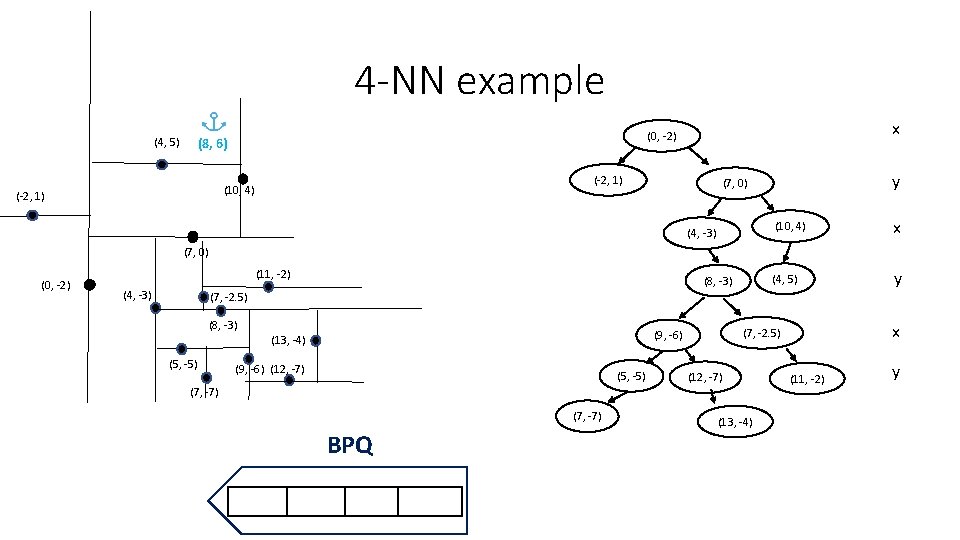
4 -NN example (4, 5) (-2, 1) (10, 4) (-2, 1) x (0, -2) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
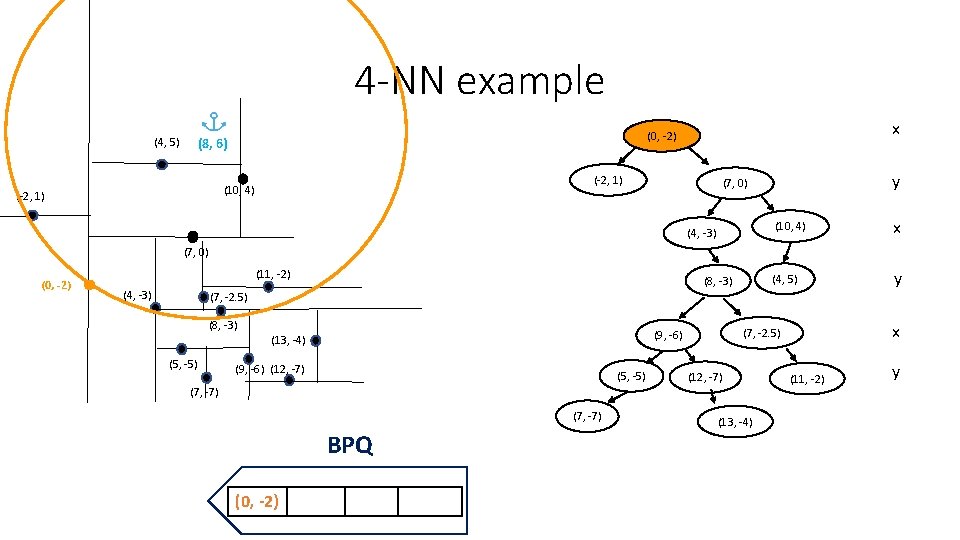
4 -NN example (4, 5) (-2, 1) (10, 4) (-2, 1) x (0, -2) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (0, -2) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
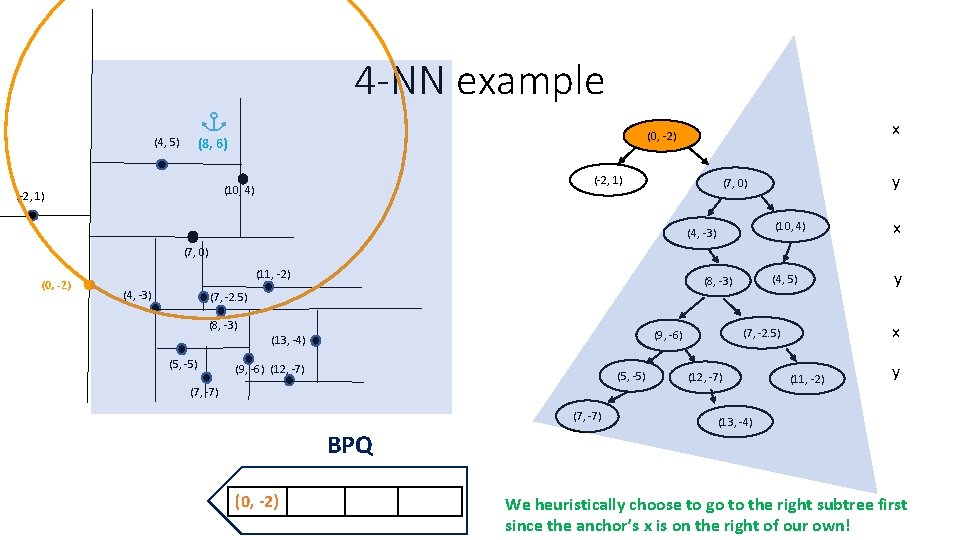
4 -NN example (4, 5) (-2, 1) (10, 4) (-2, 1) x (0, -2) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (0, -2) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (11, -2) y (13, -4) We heuristically choose to go to the right subtree first since the anchor’s x is on the right of our own!
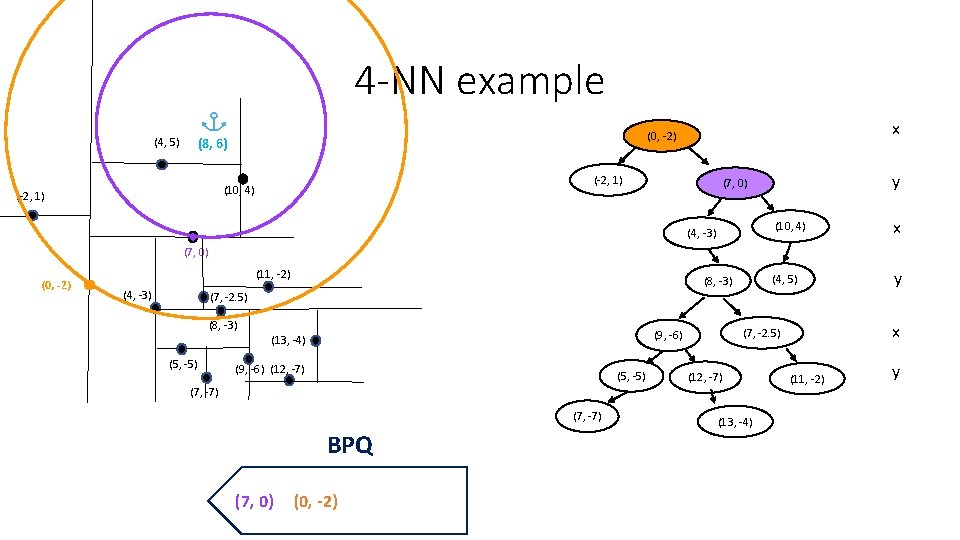
4 -NN example (4, 5) (-2, 1) (10, 4) (-2, 1) x (0, -2) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (7, 0) (0, -2) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
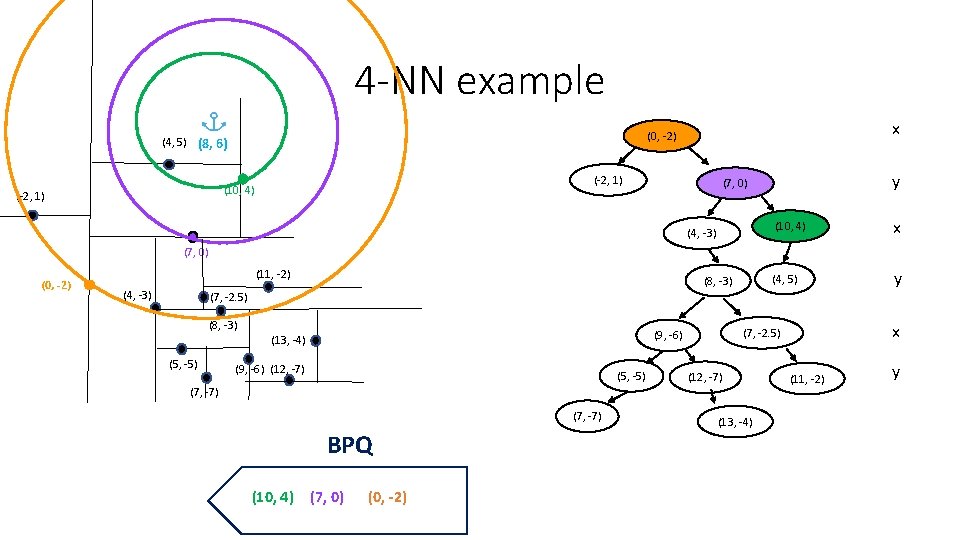
4 -NN example (-2, 1) (10, 4) (-2, 1) x (0, -2) (4, 5) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (10, 4) (7, 0) (0, -2) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
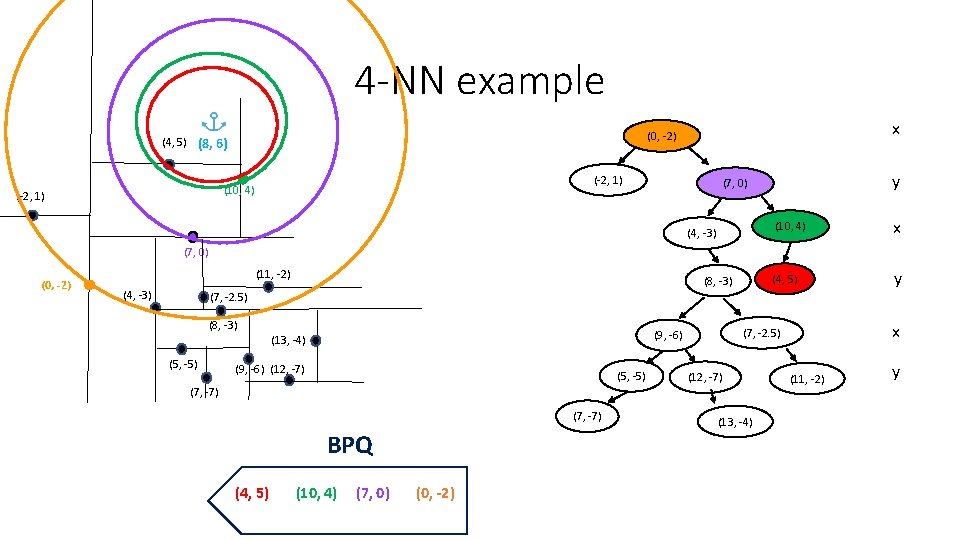
4 -NN example (-2, 1) (10, 4) (-2, 1) x (0, -2) (4, 5) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (0, -2) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
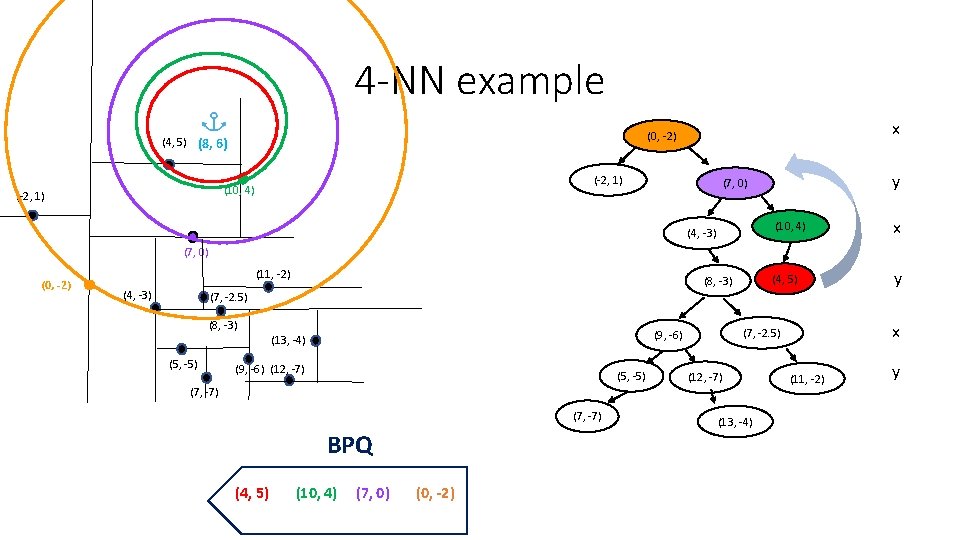
4 -NN example (-2, 1) (10, 4) (-2, 1) x (0, -2) (4, 5) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (0, -2) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
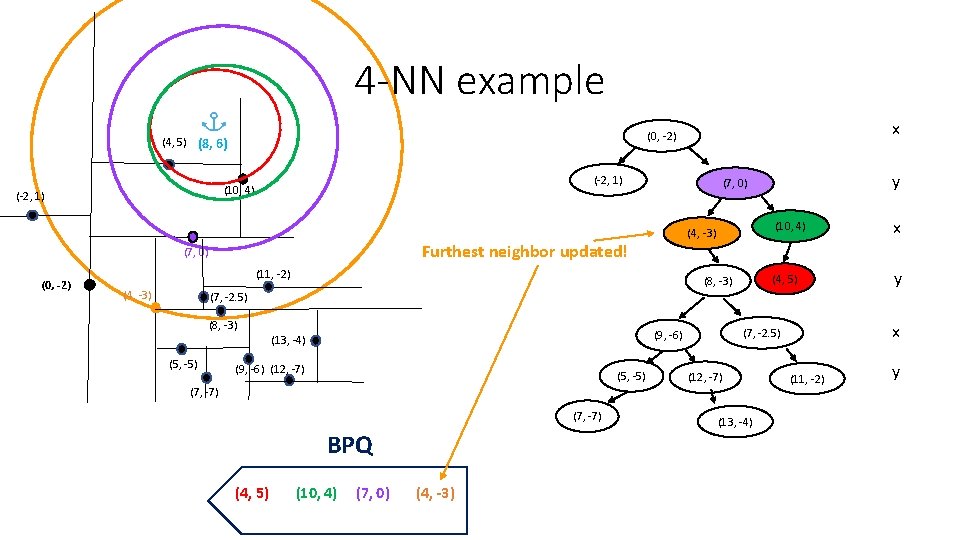
4 -NN example (-2, 1) (10, 4) (-2, 1) (4, -3) (11, -2) (4, -3) y (7, 0) Furthest neighbor updated! (7, 0) (0, -2) x (0, -2) (4, 5) (8, 6) (8, -3) (10, 4) x (4, 5) y (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (4, -3) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
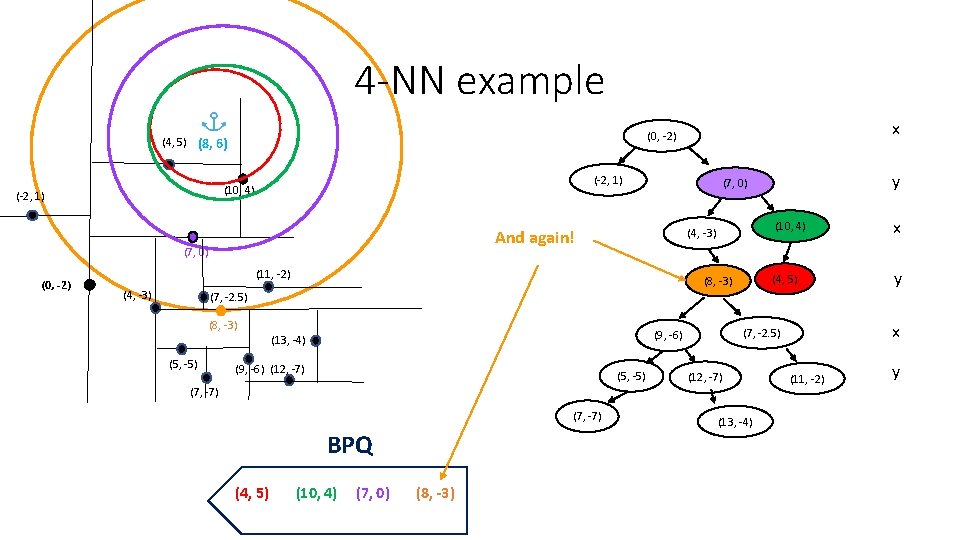
4 -NN example (-2, 1) (10, 4) (-2, 1) (4, -3) (11, -2) (4, -3) y (7, 0) And again! (7, 0) (0, -2) x (0, -2) (4, 5) (8, 6) (8, -3) (10, 4) x (4, 5) y (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (8, -3) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
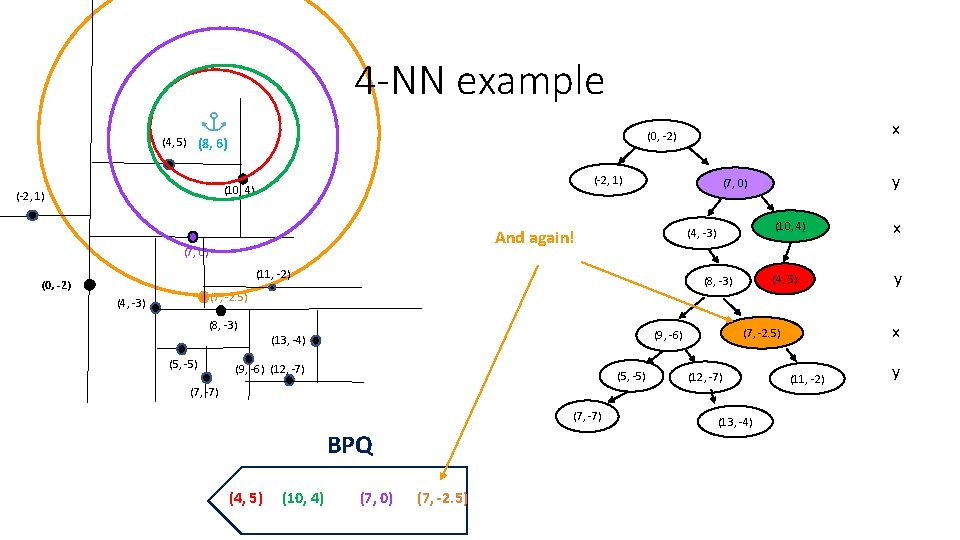
4 -NN example (-2, 1) (10, 4) (-2, 1) y (7, 0) (4, -3) And again! (7, 0) (11, -2) (0, -2) x (0, -2) (4, 5) (8, 6) (8, -3) (10, 4) x (4, 5) y (7, -2. 5) (4, -3) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (7, -2. 5) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
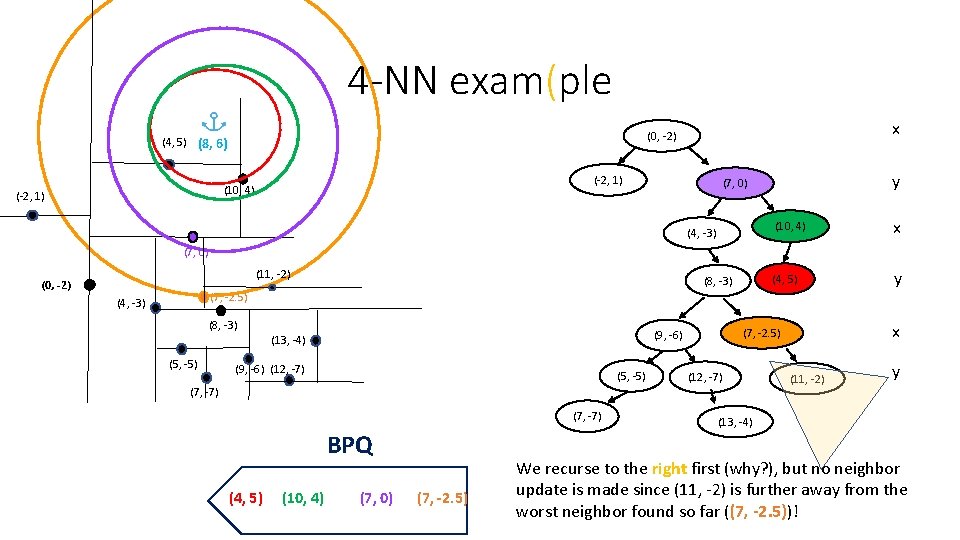
4 -NN exam(ple (-2, 1) (10, 4) (-2, 1) x (0, -2) (4, 5) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (11, -2) (0, -2) (8, -3) (7, -2. 5) (4, -3) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (7, -2. 5) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (11, -2) y (13, -4) We recurse to the right first (why? ), but no neighbor update is made since (11, -2) is further away from the worst neighbor found so far ((7, -2. 5))!
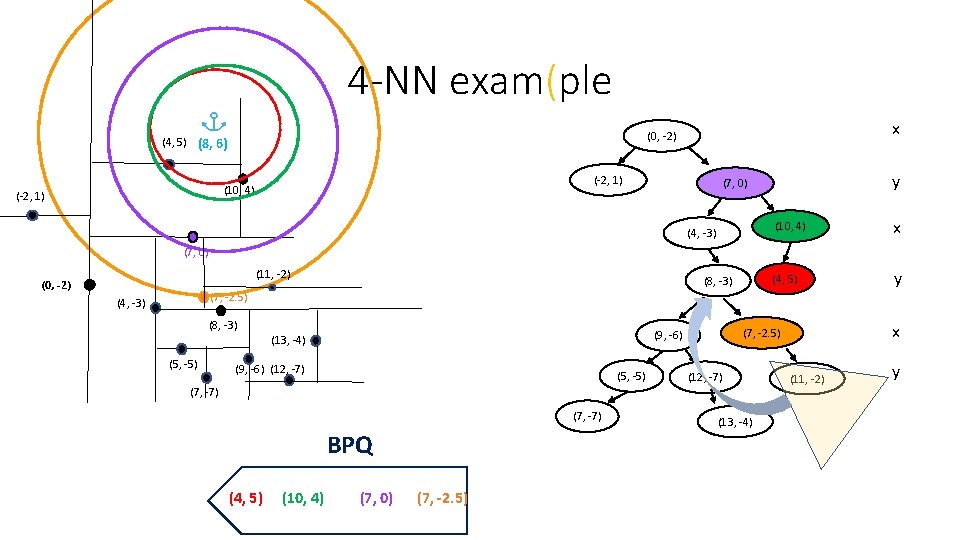
4 -NN exam(ple (-2, 1) (10, 4) (-2, 1) x (0, -2) (4, 5) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (11, -2) (0, -2) (8, -3) (7, -2. 5) (4, -3) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (7, -2. 5) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
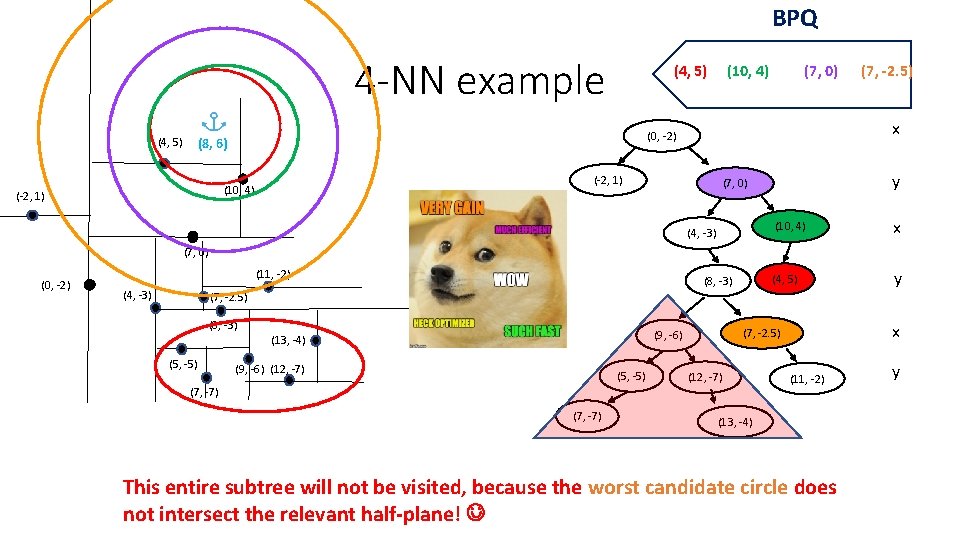
BPQ 4 -NN example (4, 5) (7, 0) (-2, 1) (10, 4) (7, -2. 5) x (0, -2) (8, 6) (-2, 1) (10, 4) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (11, -2) (13, -4) This entire subtree will not be visited, because the worst candidate circle does not intersect the relevant half-plane! y
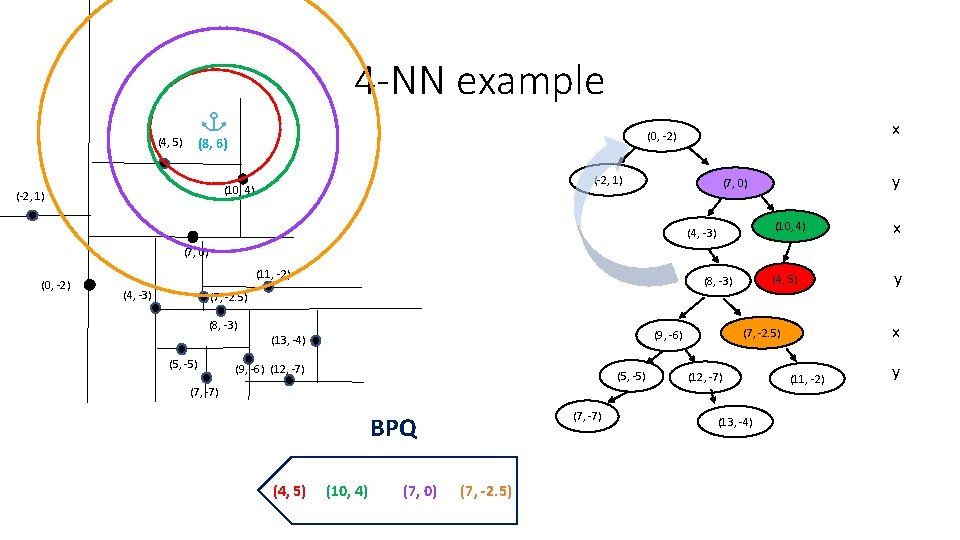
4 -NN example (4, 5) (-2, 1) (10, 4) (-2, 1) x (0, -2) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (7, -2. 5) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y
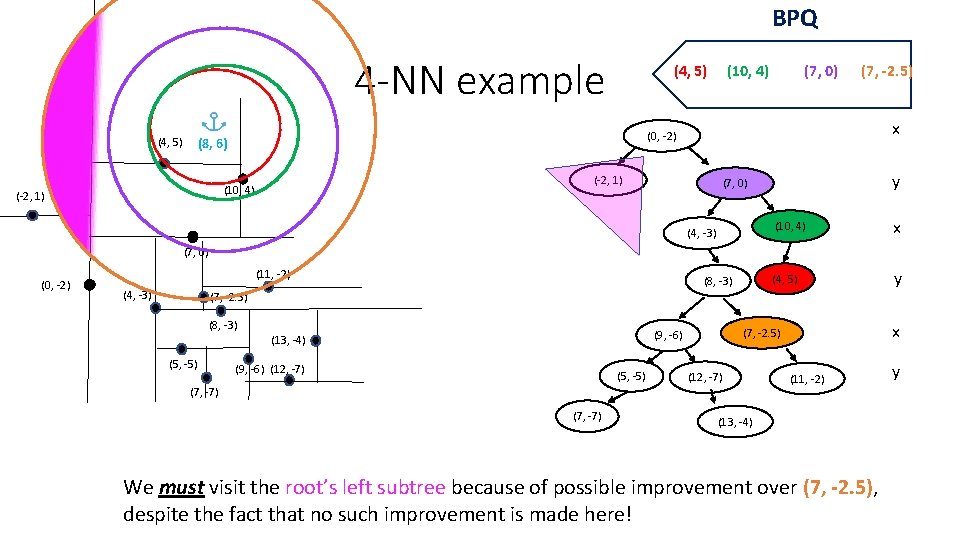
BPQ 4 -NN example (4, 5) (7, 0) (7, -2. 5) x (0, -2) (8, 6) (-2, 1) (10, 4) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) x (7, -2. 5) (9, -6) (13, -4) (12, -7) (11, -2) (13, -4) We must visit the root’s left subtree because of possible improvement over (7, -2. 5), despite the fact that no such improvement is made here! y
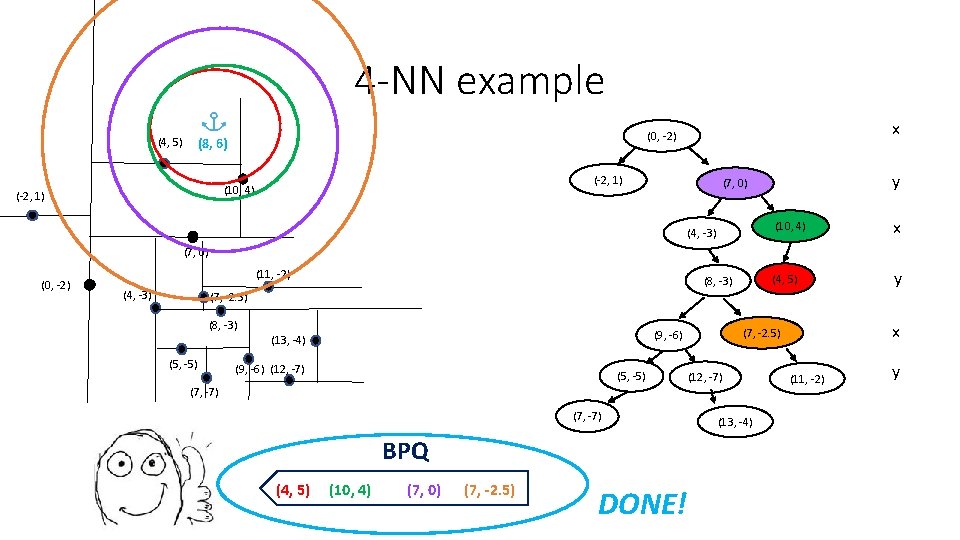
4 -NN example (4, 5) (-2, 1) (10, 4) (-2, 1) x (0, -2) (8, 6) y (7, 0) (4, -3) (10, 4) x (4, 5) y (7, 0) (0, -2) (11, -2) (4, -3) (8, -3) (7, -2. 5) (8, -3) (5, -5) (9, -6) (12, -7) (5, -5) (7, -7) BPQ (4, 5) (10, 4) (7, 0) (7, -2. 5) DONE! x (7, -2. 5) (9, -6) (13, -4) (12, -7) (13, -4) (11, -2) y

Complexity of nearest neighbor •

Complexity of nearest neighbor •

Complexity of nearest neighbor •
- Slides: 149