Karnaugh Maps Not in textbook Karnaugh Maps Kmaps

Karnaugh Maps Not in textbook

Karnaugh Maps • K-maps provide a simple approach to reducing Boolean expressions from a input-output table. • The output from the table is used to fill-in the K-map. – 1’s are used to create a Sum of Product (SOP) solution. (min terms) – 0’s are used to create a Product of Sum (POS) solution. (max terms)

Min Terms • Canonical representation of a Boolean expression is in the form of ^ v ~ (AND, OR, NOT). – Example: A^B v ~A^~B v A^~B (AB + AB) • Candidates for canonical representation are taken from the truth table (input-output). • Candidates are identified where the output is “ 1”. (Max Term canonical representation candidates are identified by “ 0”)

Min Terms Min terms are taken directly from the truth tables. Where ever there is a “ 1” for an output, F(), we note the min term value and place a “ 1” in the K-map corresponding to the min term value of the table. Min term short hand is often used to replace a full input-output table. The short hand indicate the variables and the min terms that are “ 1”. Example: f(A, B, C) = S (1, 5, 7)

Examples f(A, B, C) = S (0, 1, 5, 7) min term 0 1 2 3 A 0 0 1 1 Input B 0 1 Output F(A, B) 1 1 min term 0 1 2 3 4 5 6 7 A 0 0 1 1 Input B 0 0 1 1 f(A, B) = S (1, 2) C 0 1 0 1 Output F(A, B, C) 1 1 1 1

K-Map Tables • K-map tables are organized based on the number of variables. – Example: showing min terms in italic bold.

K-Map Examples Reducing a Boolean expression using K-map 1. Identify min terms (from table or function form) 2. Fill-in appropriate K-map. 3. Group min terms in largest grouping using 4 -neighbor rule. 1. a min term is a number if it is either to the right, left, top, or bottom. 2. K-map edges are connected as neighbors. 4. Write out the groupings as the reduced expression (circuit). ~B f(A, B) = S (0, 3) B AB 0 ~A 0 1 A 1 f(A, B) = ~A^~B v A^B 1 1

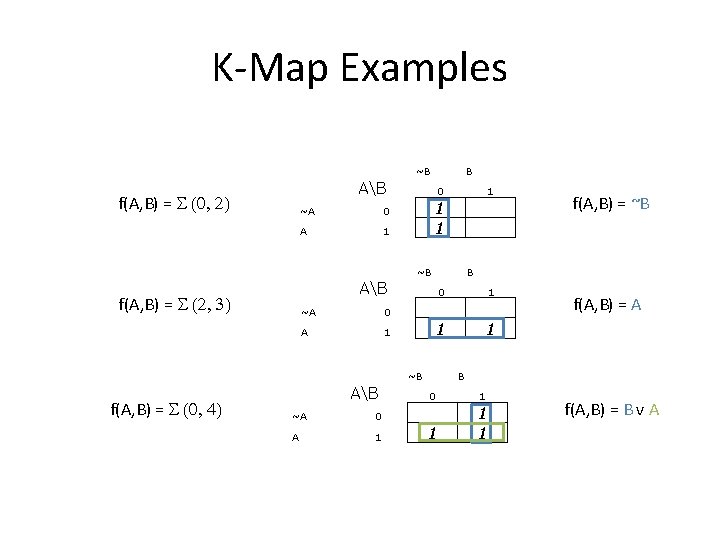
K-Map Examples ~B B AB f(A, B) = S (0, 2) ~A 0 A 1 0 1 1 1 ~B B AB f(A, B) = S (2, 3) ~A 0 A 1 0 1 1 1 ~B f(A, B) = S (0, 4) AB ~A 0 A 1 f(A, B) = ~B f(A, B) = A B 0 1 1 f(A, B) = B v A

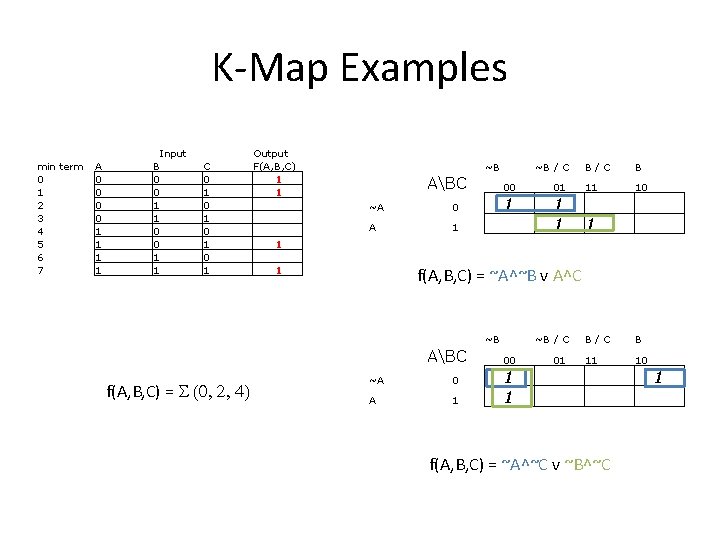
K-Map Examples min term 0 1 2 3 4 5 6 7 A 0 0 1 1 Input B 0 0 1 1 C 0 1 0 1 Output F(A, B, C) 1 1 1 1 ~B ABC ~A 0 A 1 ~B / C B 10 00 01 11 1 1 f(A, B, C) = ~A^~B v A^C ~B ABC f(A, B, C) = S (0, 2, 4) B/C ~A 0 A 1 ~B / C 00 01 B/C B 11 10 1 1 f(A, B, C) = ~A^~C v ~B^~C 1

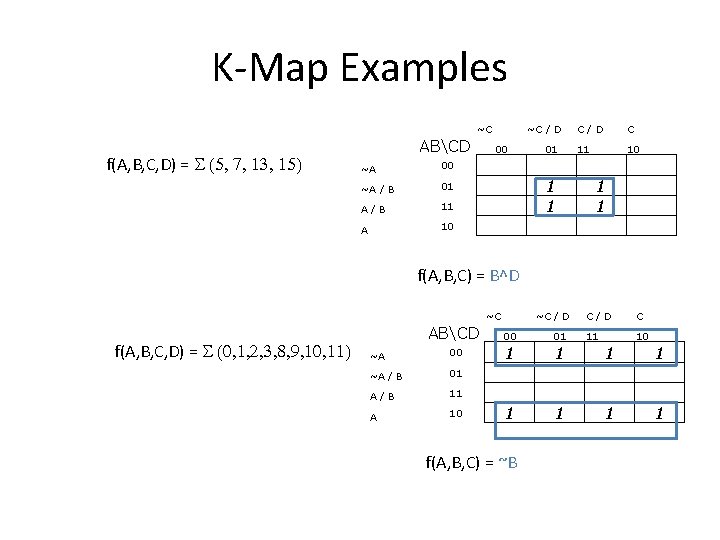
K-Map Examples ~C f(A, B, C, D) = S (5, 7, 13, 15) ABCD ~A 00 ~A / B 01 A/B 11 A 10 ~C / D 00 01 C/D C 11 10 1 1 ~C / D C/D C 11 10 f(A, B, C) = B^D ~C f(A, B, C, D) = S (0, 1, 2, 3, 8, 9, 10, 11) ABCD 00 01 ~A 00 1 1 ~A / B 01 A/B 11 A 10 1 1 f(A, B, C) = ~B

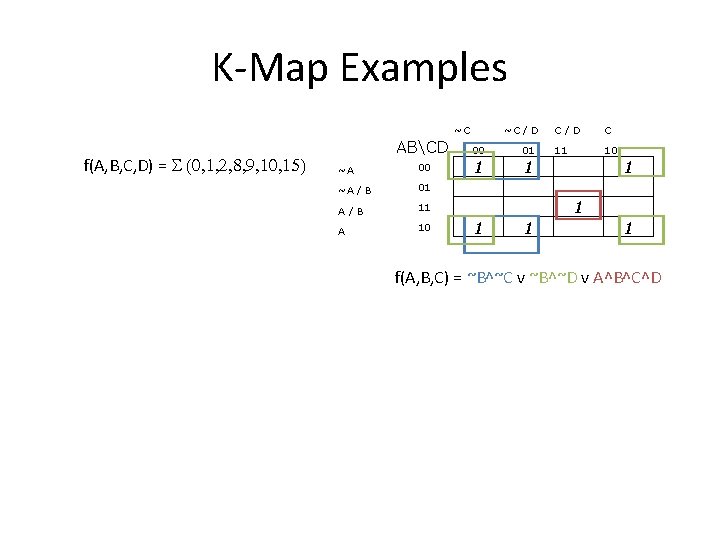
K-Map Examples ~C f(A, B, C, D) = S (0, 1, 2, 8, 9, 10, 15) ~C / D ABCD 00 01 ~A 00 1 1 ~A / B 01 A/B 11 A 10 C/D C 11 10 1 1 1 f(A, B, C) = ~B^~C v ~B^~D v A^B^C^D

HMWK Due 2/4 1. Build the input-output table from the following min term list of 4 -variables: S (5, 7, 10, 11, 14, 15) 2. Using a K-map reduce the expression from 1 such that you minimize the number of connectives (AND, OR, NOT). Remember the answer should be in the sum of product form.