Karnaugh Maps Maurice Karnaugh Logic Symbols Not v

Karnaugh Maps Maurice Karnaugh

Logic Symbols • ¬ • Not • v • Or • ∧ • And

Consider this expression… ¬Av¬B • Draw this logic circuit • Write the truth table A 0 1 1 0 B 1 0 Output

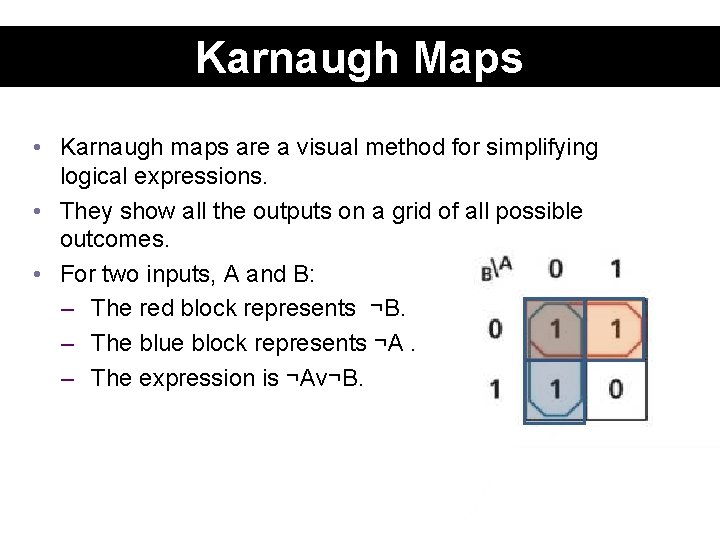
Karnaugh Maps • Karnaugh maps are a visual method for simplifying logical expressions. • They show all the outputs on a grid of all possible outcomes. • For two inputs, A and B: – The red block represents ¬B. – The blue block represents ¬A. – The expression is ¬Av¬B.

Take this expression… – – A 0 1 1 0 A∧Bv. A∧¬B Draw the logic circuit and truth table B 1 0 Output

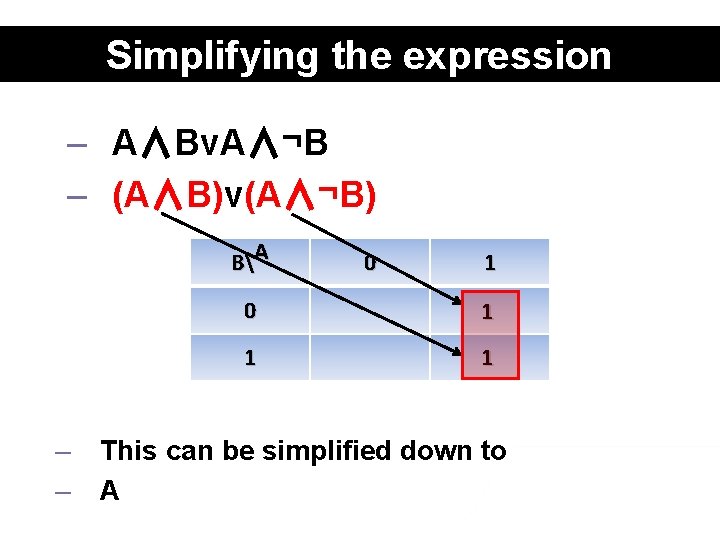
Simplifying the expression – A∧Bv. A∧¬B – (A∧B)v(A∧¬B) BA – – 0 1 1 1 This can be simplified down to A

Take this expression… – – A∧B∧Cv. A∧¬B∧Cv. A∧B∧¬C Simplify this expression using a Kmap First split the expression into 3 parts (A∧B∧C) v (A∧¬B∧C) v (A∧B∧¬C) CAB 00 01 11 0 1 10 1

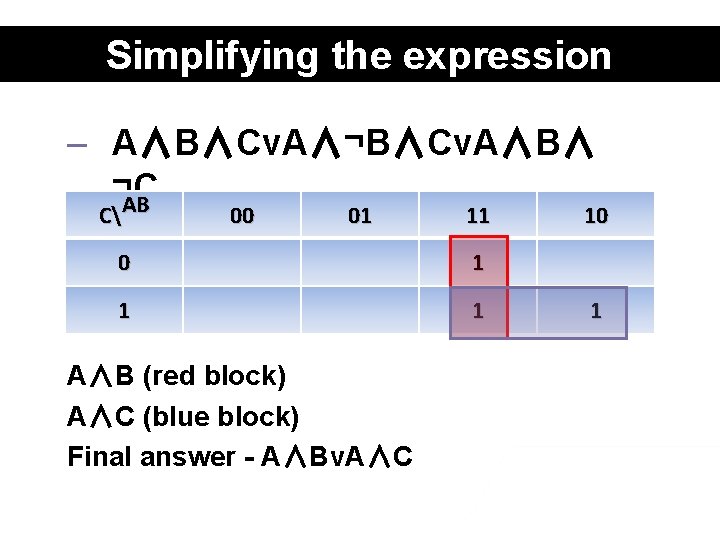
Simplifying the expression – A∧B∧Cv. A∧¬B∧Cv. A∧B∧ ¬C AB C 00 01 11 0 1 1 1 A∧B (red block) A∧C (blue block) Final answer - A∧Bv. A∧C 10 1

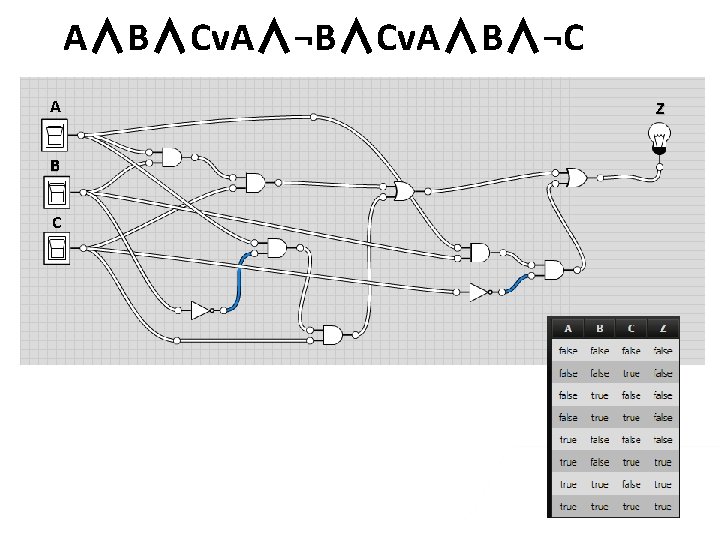
A∧B∧Cv. A∧¬B∧Cv. A∧B∧¬C A B C Z

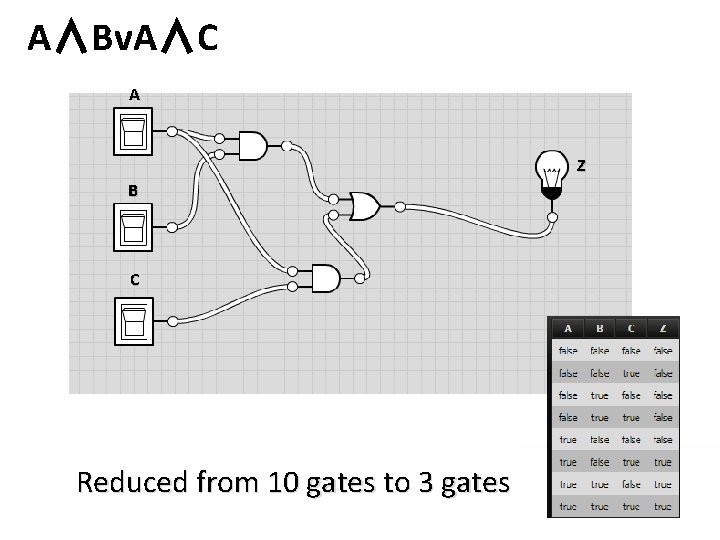
A∧Bv. A∧C A Z B C Reduced from 10 gates to 3 gates

Take this expression… – – A∧B∧Cv. A∧¬B∧C Simply this express using a Kmap First split the expression into 2 parts (A∧B∧C) v (A∧¬B∧C) CAB 00 01 11 10 1 1 0 1

Simplifying the expression – A∧B∧Cv. A∧¬B∧C CAB 00 01 11 10 1 1 0 1 A∧C (red block) Final answer - A∧C

Take this expression… – – A∧Bv¬C∧¬D Simply this expression using a Kmap First split the expression into parts (A∧B)v(¬C∧¬D) CDAB 00 01 11 10 00 1 1 01 1 1 10 1 1

Simplifying the expression CDAB 00 01 11 10 00 1 1 01 1 1 10 1 1 (A∧B)v(¬C∧¬D) B (red block) ¬C∧¬D (blue block) Final Answer - Bv¬C∧¬D

Simplifying further • Bv¬C∧¬D • Using De. Morgans Theorem this can be further simplified • ¬C∧¬D = ¬(Cv. D) • Bv¬(Cv. D)

Take this expression… – – – ¬A∧¬B∧¬Cv¬A∧Bv. A∧B∧¬Cv. A∧ C Simply this express using a Kmap First split the expression into 4 parts – (¬A∧¬B∧¬C)v(¬A∧B)v(A∧B∧¬C)v(A∧C) CAB 00 01 11 0 1 1 1 10 1

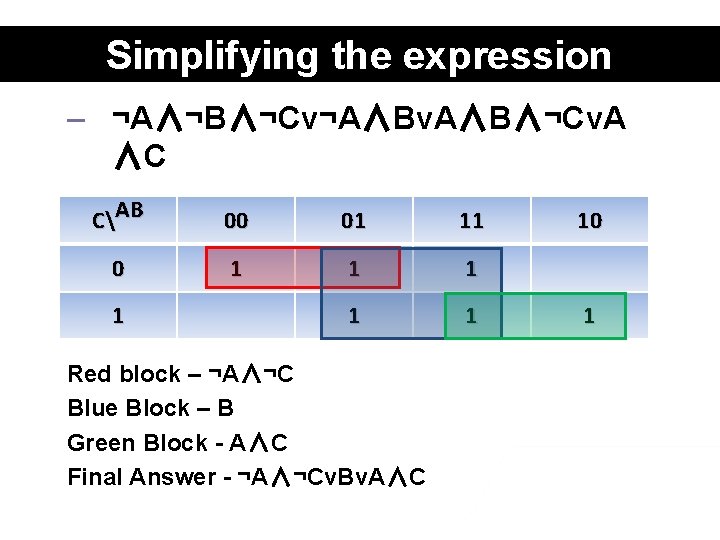
Simplifying the expression – ¬A∧¬B∧¬Cv¬A∧Bv. A∧B∧¬Cv. A ∧C CAB 00 01 11 0 1 1 1 Red block – ¬A∧¬C Blue Block – B Green Block - A∧C Final Answer - ¬A∧¬Cv. Bv. A∧C 10 1

Take this expression… – ¬A∧¬B∧Dv¬A∧B∧Dv A∧¬C∧Dv. A∧D∧C – Simply this express using a Kmap – First split the expression into parts – (¬A∧¬B∧D)v(¬A∧B∧D)v(A∧¬C∧D)v(A AB CD∧D∧C) 00 01 11 10 00 01 1 10

Simplifying the expression CDAB 00 01 11 10 01 1 1 11 1 1 00 10 Red block represents D Final Answer - D

Take this expression… – A∧B∧C∧¬Dv. A∧¬B∧C∧¬Dv. A∧B∧¬C∧¬Dv. A∧ ¬B∧¬C∧¬D – – Simply this expression using a Kmap First split the expression into parts – (A∧B∧C∧¬D)v(A∧¬B∧C∧¬D)v(A∧B∧¬C∧¬D)v(A∧ ¬B∧¬C∧¬D) CDAB 00 00 01 11 10 1 1

Simplifying the expression CDAB 00 00 01 11 10 1 1 01 11 10 The block can wrap around the table (both horizontally and vertically) Final Answer - A∧¬D

Take this expression… – – (B ∧ ¬ A ∧ ¬ C ∧ ¬ D) v (¬ A ∧ ¬ B ∧ ¬ C ∧ ¬ D) Simply this expression using a Kmap First split the expression into parts (B ∧ ¬ A ∧ ¬ C ∧ ¬ D) v (¬ A ∧ ¬ B ∧ ¬ C ∧ ¬ D) CDAB 00 00 1 01 11 10 1

Simplifying the expression CDAB 00 00 1 01 11 10 The block wraps horizontally around the table Final Answer – (¬B ∧ ¬ C ∧ ¬ D)

Rules for creating groupings § Groups must contain 1, 2, 4, 8… number of 1 s in a block § Make groups as large as possible § No diagonal blocks § Create as few groups as possible § Groups can overlap § Groups can wrap around the table horizontally and vertically