Karnaugh Maps Kmap A Kmap is a collection

Karnaugh Maps (K-map) • A K-map is a collection of squares – Each square represents a minterm – The collection of squares is a graphical representation of a – – Boolean function Adjacent squares differ in the value of one variable Alternative algebraic expressions for the same function are derived by recognizing patterns of squares • The K-map can be viewed as – A reorganized version of the truth table – A topologically-warped Venn diagram as used to visualize sets in algebra of sets KU College of Engineering Elec 204: Digital Systems Design 1

Some Uses of K-Maps • Provide a means for: – Finding optimum or near optimum • SOP and POS standard forms, and • two-level AND/OR and OR/AND circuit implementations for functions with small numbers of variables – Visualizing concepts related to manipulating Boolean expressions, and – Demonstrating concepts used by computer-aided design programs to simplify large circuits KU College of Engineering Elec 204: Digital Systems Design 2

Two Variable Maps • A 2 -variable Karnaugh Map: y=0 y=1 – Note that minterm m 0 and m 0 = m 1 = minterm m 1 are “adjacent” x=0 xy xy and differ in the value of the variable y x = 1 m 2 = m 3 = – Similarly, minterm m 0 and xy xy minterm m 2 differ in the x variable. – Also, m 1 and m 3 differ in the x variable as well. – Finally, m 2 and m 3 differ in the value of the variable y KU College of Engineering Elec 204: Digital Systems Design 3

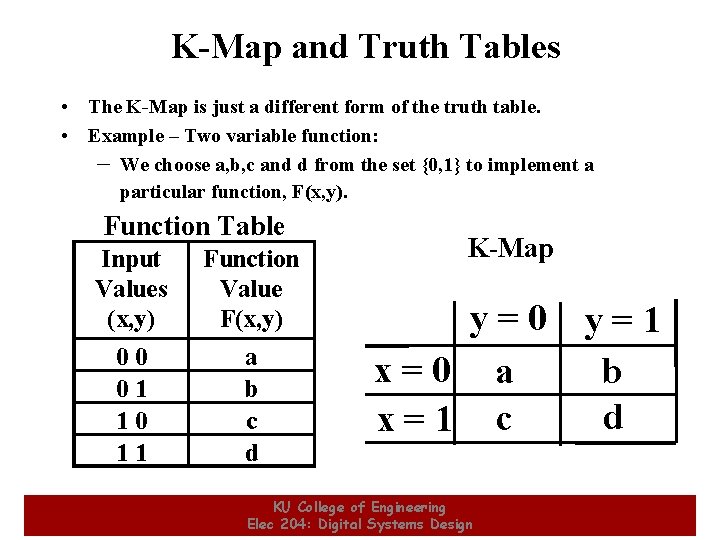
K-Map and Truth Tables • The K-Map is just a different form of the truth table. • Example – Two variable function: – We choose a, b, c and d from the set {0, 1} to implement a particular function, F(x, y). Function Table Input Values (x, y) Function Value F(x, y) 00 01 10 11 a b c d K-Map y=0 x=0 a x=1 c KU College of Engineering Elec 204: Digital Systems Design y=1 b d 4

K-Map Function Representation F=x y=0 y=1 • Example: F(x, y) = x • x=0 0 0 x=1 1 1 For function F(x, y), the two adjacent cells containing 1’s can be combined using the Minimization Theorem: F( x , y ) = x y + x y = x KU College of Engineering Elec 204: Digital Systems Design 5

K-Map Function Representation G = x+y y = 0 y = 1 • Example: G(x, y) = x + y x=0 0 1 x=1 1 1 • For G(x, y), two pairs of adjacent cells containing 1’s can be combined using the Minimization Theorem: G( x , y ) = (x y + x y )+ (xy + x y )= x + y Duplicate x y KU College of Engineering Elec 204: Digital Systems Design 6

Three Variable Maps • A three-variable K-map: yz=00 yz=01 yz=10 x=0 m 1 m 3 m 2 x=1 m 4 m 5 m 7 m 6 • Where each minterm corresponds to the product terms: yz=00 yz=01 yz=10 x=0 x y z xyz xyz xyz x=1 xyz • Note that if the binary value for an index differs in one bit position, the minterms are adjacent on the K-Map KU College of Engineering Elec 204: Digital Systems Design 7

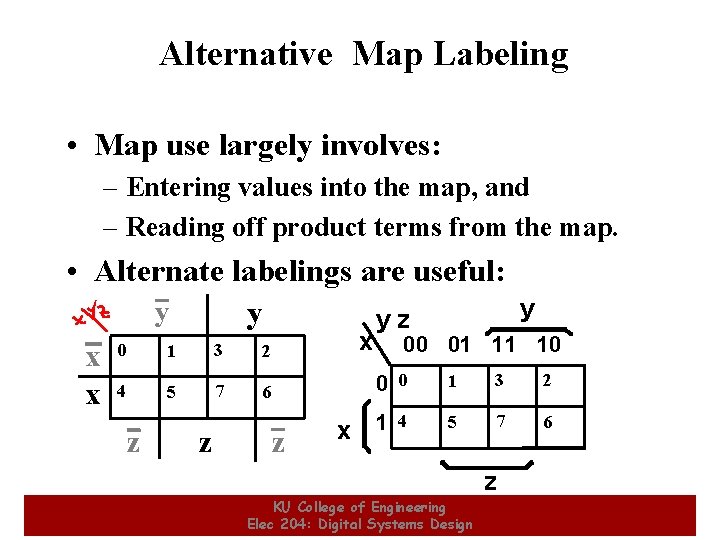
Alternative Map Labeling • Map use largely involves: – Entering values into the map, and – Reading off product terms from the map. • Alternate labelings are useful: y yz x 00 01 11 10 0 3 2 1 x 3 2 1 0 0 4 7 6 5 x 7 6 5 1 4 x z z KU College of Engineering Elec 204: Digital Systems Design 8

Example Functions • By convention, we represent the minterms of F by a "1" in the map and leave the minterms of blank F • Example: y 0 1 x 41 • Example: 5 3 2 7 6 1 1 z • Learn the locations of the 8 indices based on the variable order shown (x, most significant and z, least significant) on the map boundaries 0 x 41 KU College of Engineering Elec 204: Digital Systems Design 1 1 y 3 1 7 1 5 2 6 1 z 9

Combining Squares • By combining squares, we reduce number of literals in a product term, reducing the literal cost, thereby reducing the other two cost criteria • On a 3 -variable K-Map: – One square represents a minterm with three variables – Two adjacent squares represent a product term with two variables – Four “adjacent” terms represent a product term with one variable – Eight “adjacent” terms is the function of all ones (no variables) = 1. KU College of Engineering Elec 204: Digital Systems Design 10

Example: Combining Squares y • Example: Let x 0 1 4 5 3 1 7 1 2 1 6 1 z • Applying the Minimization Theorem three times: F( x , y , z ) = x y z + x y z = yz + y z =y • Thus the four terms that form a 2 × 2 square correspond to the term "y". KU College of Engineering Elec 204: Digital Systems Design 11

Three-Variable Maps • Reduced literal product terms for SOP standard forms correspond to rectangles on K-maps containing cell counts that are powers of 2. • Rectangles of 2 cells represent 2 adjacent minterms; of 4 cells represent 4 minterms that form a “pairwise adjacent” ring. • Rectangles can contain non-adjacent cells as illustrated by the “pairwise adjacent” ring above. KU College of Engineering Elec 204: Digital Systems Design 12

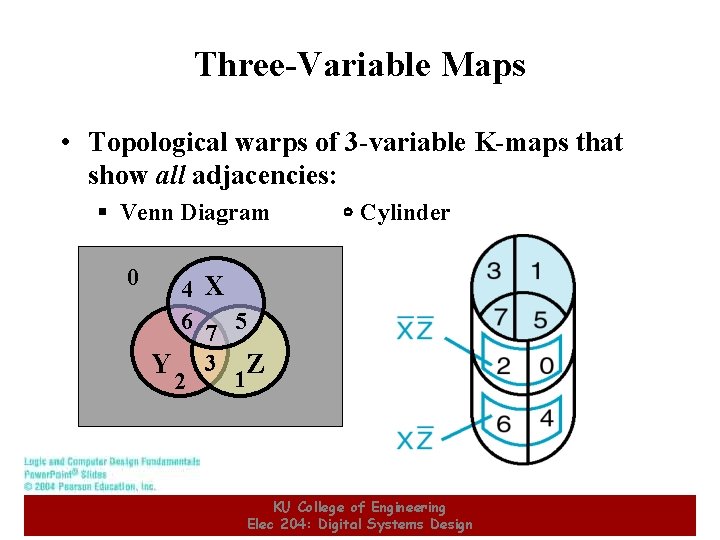
Three-Variable Maps • Topological warps of 3 -variable K-maps that show all adjacencies: § Venn Diagram 0 Cylinder 4 X 6 7 5 Y 3 Z 1 2 KU College of Engineering Elec 204: Digital Systems Design 13

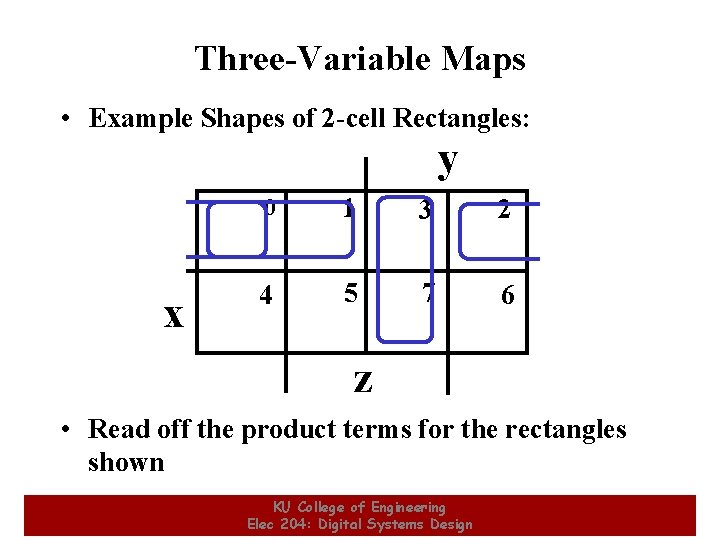
Three-Variable Maps • Example Shapes of 2 -cell Rectangles: y x 0 1 3 2 4 5 7 6 z • Read off the product terms for the rectangles shown KU College of Engineering Elec 204: Digital Systems Design 14

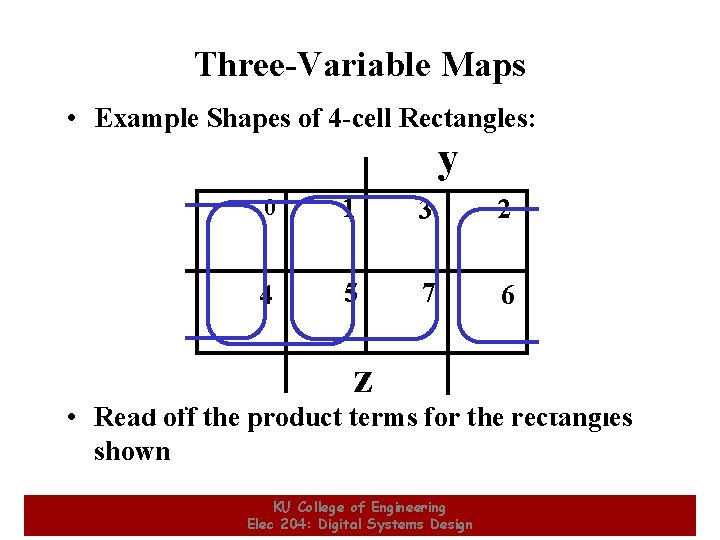
Three-Variable Maps • Example Shapes of 4 -cell Rectangles: y x 0 1 3 2 4 5 7 6 z • Read off the product terms for the rectangles shown KU College of Engineering Elec 204: Digital Systems Design 15

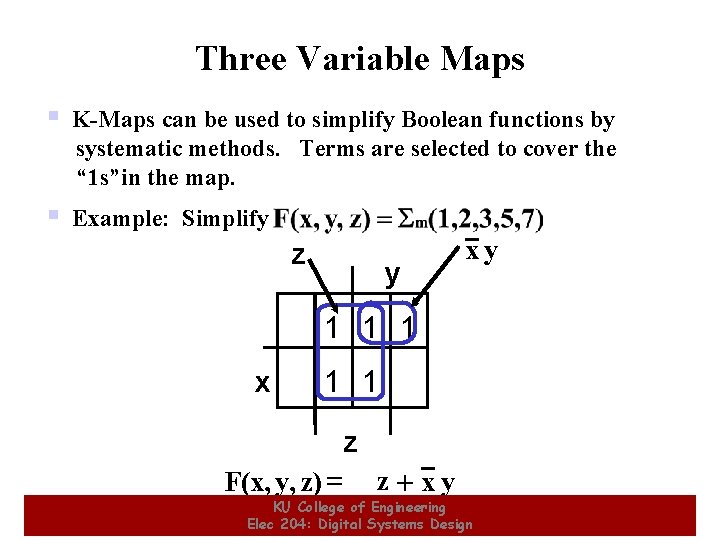
Three Variable Maps § K-Maps can be used to simplify Boolean functions by systematic methods. Terms are selected to cover the “ 1 s”in the map. § Example: Simplify z y xy 1 1 1 x 1 1 z F(x, y, z) = z+xy KU College of Engineering Elec 204: Digital Systems Design 16

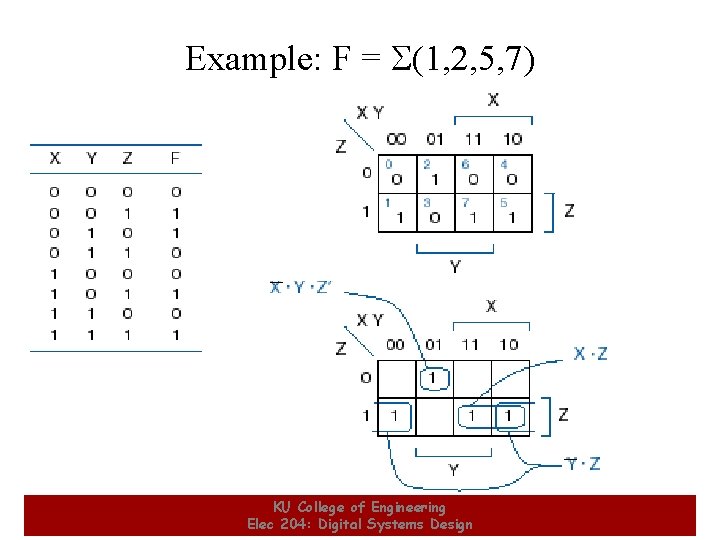
Example: F = S(1, 2, 5, 7) KU College of Engineering Elec 204: Digital Systems Design 17

Three-Variable Map Simplification • Use a K-map to find an optimum SOP equation for KU College of Engineering Elec 204: Digital Systems Design 18

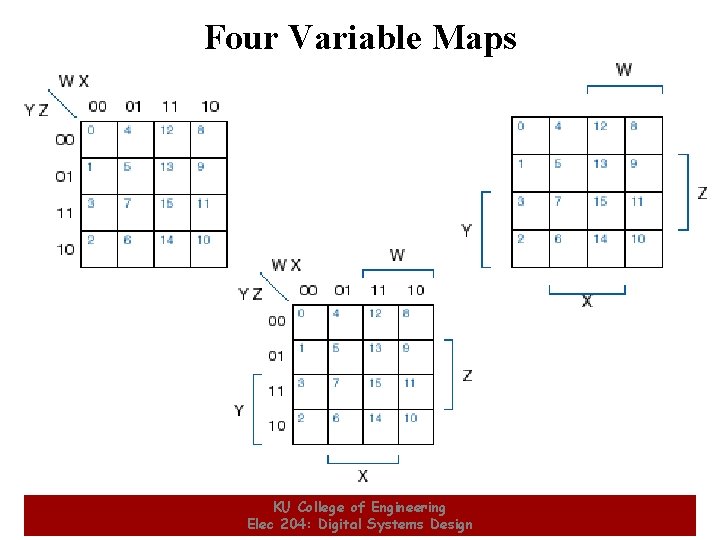
Four Variable Maps KU College of Engineering Elec 204: Digital Systems Design 19

Four Variable Terms § Four variable maps can have rectangles corresponding to: • A single 1 = 4 variables, (i. e. Minterm) • Two 1 s = 3 variables, • Four 1 s = 2 variables • Eight 1 s = 1 variable, • Sixteen 1 s = zero variables (i. e. Constant "1") KU College of Engineering Elec 204: Digital Systems Design 20

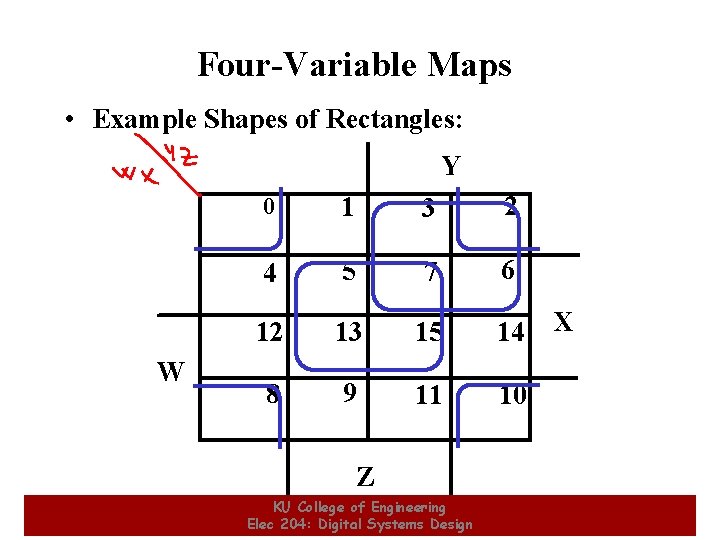
Four-Variable Maps • Example Shapes of Rectangles: Y W 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 X Z KU College of Engineering Elec 204: Digital Systems Design 21

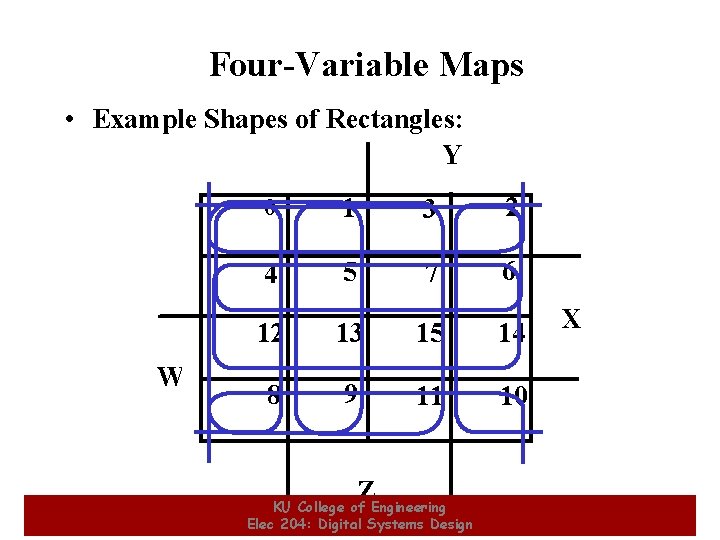
Four-Variable Maps • Example Shapes of Rectangles: Y W 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 Z KU College of Engineering Elec 204: Digital Systems Design X 22

Karnaugh-map usage • Plot 1 s corresponding to minterms of function. • Circle largest possible rectangular sets of 1 s. – # of 1 s in set must be power of 2 – OK to cross edges • Read off product terms, one per circled set. – Variable is 1 ==> include variable – Variable is 0 ==> include complement of variable – Variable is both 0 and 1 ==> variable not included • Circled sets and corresponding product terms are called “implicants” • If a minterm is included in only one prime implicant, then that prime implicant is essential. • Minimum number of gates and gate inputs KU College of Engineering Elec 204: Digital Systems Design 23

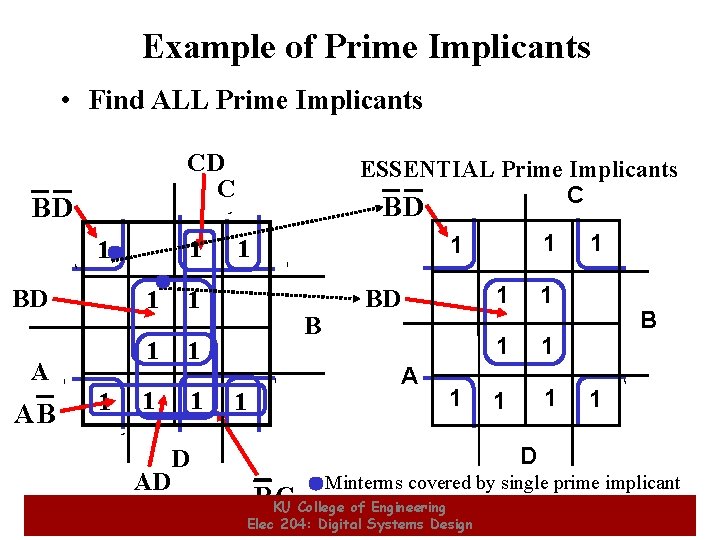
Example of Prime Implicants • Find ALL Prime Implicants CD C BD 1 1 BD A AB 1 1 1 1 D AD ESSENTIAL Prime Implicants C BD B 1 1 1 BD 1 1 B A 1 1 1 D Minterms covered by single prime implicant B KU C College of Engineering Elec 204: Digital Systems Design 24

Prime Implicant Practice • Find all prime implicants for: KU College of Engineering Elec 204: Digital Systems Design 25

Another Example • Find all prime and essential prime implicants for: – Hint: There are seven prime implicants! KU College of Engineering Elec 204: Digital Systems Design 26

Optimization Algorithm • Find all prime implicants. • Include all essential prime implicants in the solution • Select a minimum cost set of non-essential prime implicants to cover all minterms not yet covered: – Obtaining an optimum solution: See Reading Supplement More on Optimization – Obtaining a good simplified solution: Use the Selection Rule KU College of Engineering Elec 204: Digital Systems Design 27

Prime Implicant Selection Rule • Minimize the overlap among prime implicants as much as possible. In particular, in the final solution, make sure that each prime implicant selected includes at least one minterm not included in any other prime implicant selected. KU College of Engineering Elec 204: Digital Systems Design 28