Karnaugh Map Introduction Venn Diagram 2 variable Kmap

Karnaugh Map • • • Introduction Venn Diagram 2 variable K-map 3 variable K-map 4 variable K-map simplification MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 1

Karnaugh Map • • Convert to Minterm Form Simplest SOP expression Produce POS expression Don’t care condition MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 2

Karnaugh Map -Introduction • Systematic method to get simplest Boolean SOP expression • Objective: Minimum number of literal • Dramatic technique based on special Venn Diagram Form • Advantage: Easy with visual aid • Disadvantage: Limited to five or six variables MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 3

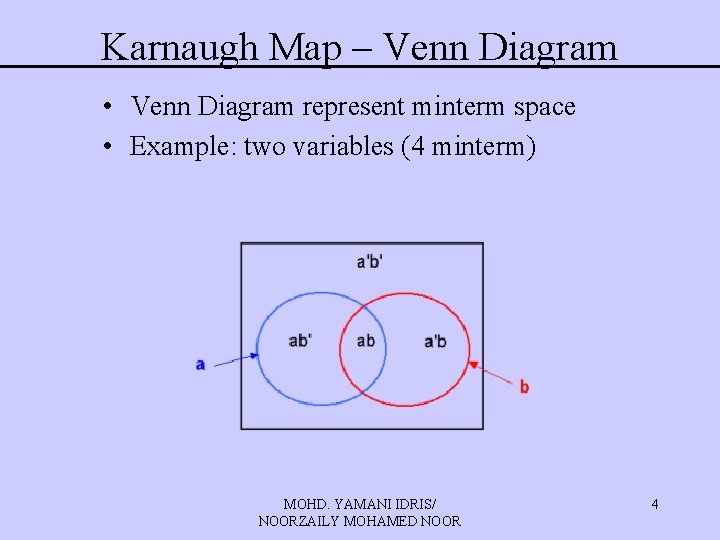
Karnaugh Map – Venn Diagram • Venn Diagram represent minterm space • Example: two variables (4 minterm) MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 4

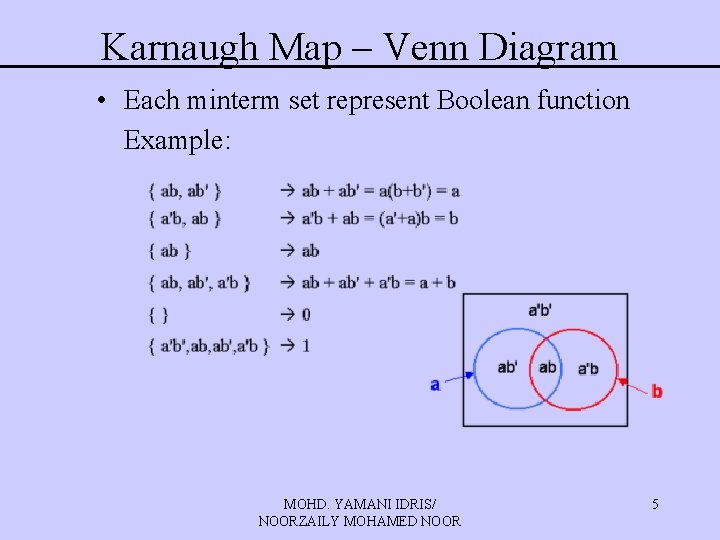
Karnaugh Map – Venn Diagram • Each minterm set represent Boolean function Example: MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 5

Karnaugh Map – 2 variable • K-map is abstract form, Venn diagram is arranged as square matrix, where – Each square represent one minterm – Adjacent square is always differentiated with one literal (therefore theorem a+a’ can be used) • For two variable case (e. g. variable a, b), map can be drawn as MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 6

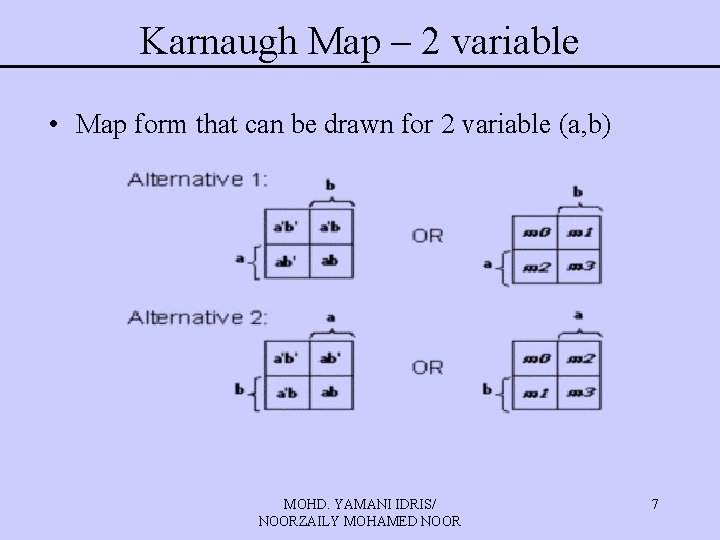
Karnaugh Map – 2 variable • Map form that can be drawn for 2 variable (a, b) MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 7

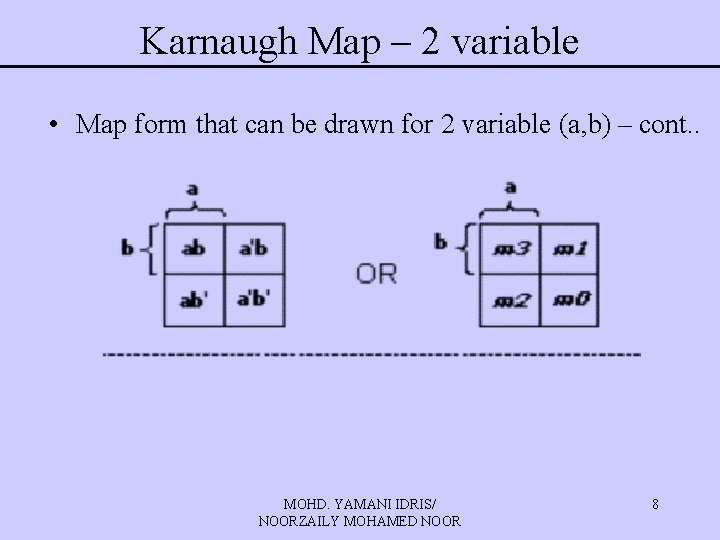
Karnaugh Map – 2 variable • Map form that can be drawn for 2 variable (a, b) – cont. . MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 8

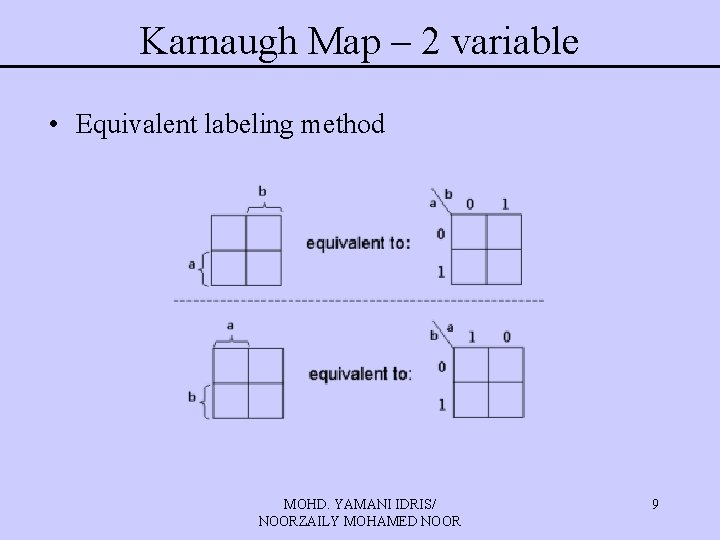
Karnaugh Map – 2 variable • Equivalent labeling method MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 9

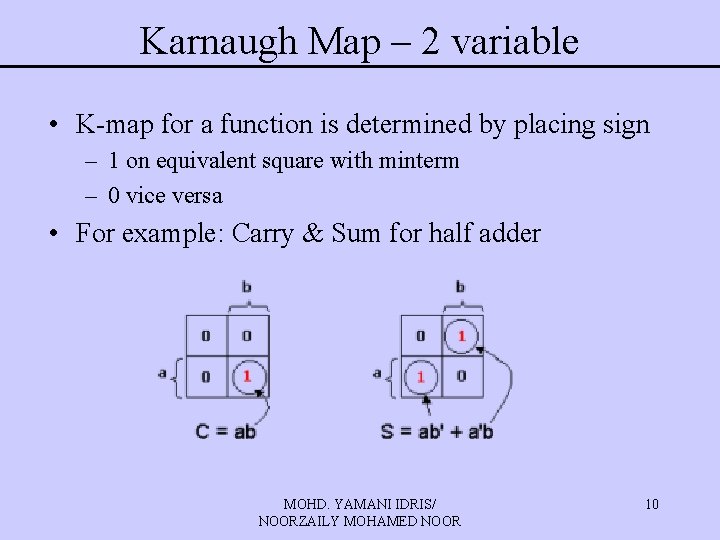
Karnaugh Map – 2 variable • K-map for a function is determined by placing sign – 1 on equivalent square with minterm – 0 vice versa • For example: Carry & Sum for half adder MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 10

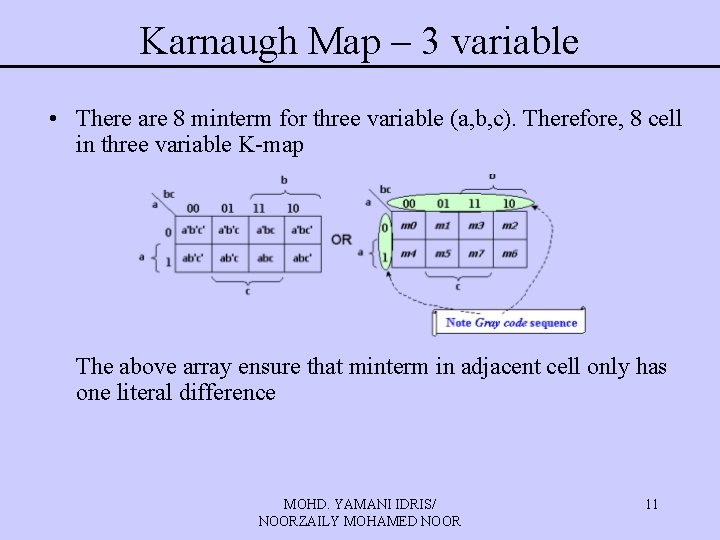
Karnaugh Map – 3 variable • There are 8 minterm for three variable (a, b, c). Therefore, 8 cell in three variable K-map The above array ensure that minterm in adjacent cell only has one literal difference MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 11

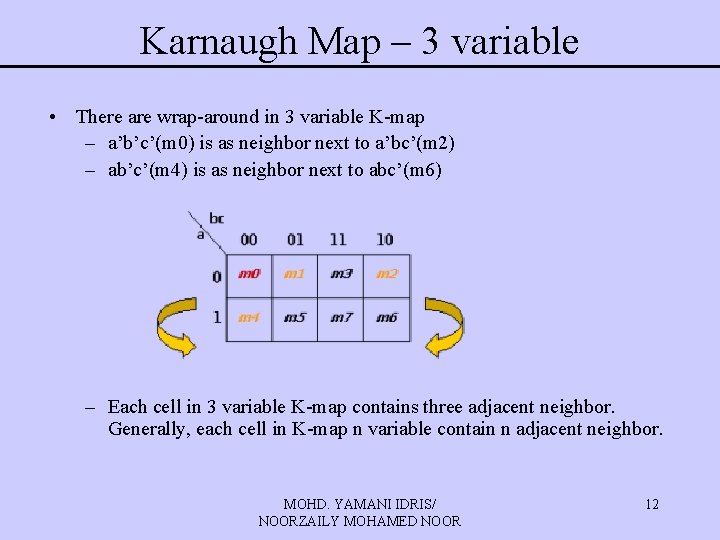
Karnaugh Map – 3 variable • There are wrap-around in 3 variable K-map – a’b’c’(m 0) is as neighbor next to a’bc’(m 2) – ab’c’(m 4) is as neighbor next to abc’(m 6) – Each cell in 3 variable K-map contains three adjacent neighbor. Generally, each cell in K-map n variable contain n adjacent neighbor. MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 12

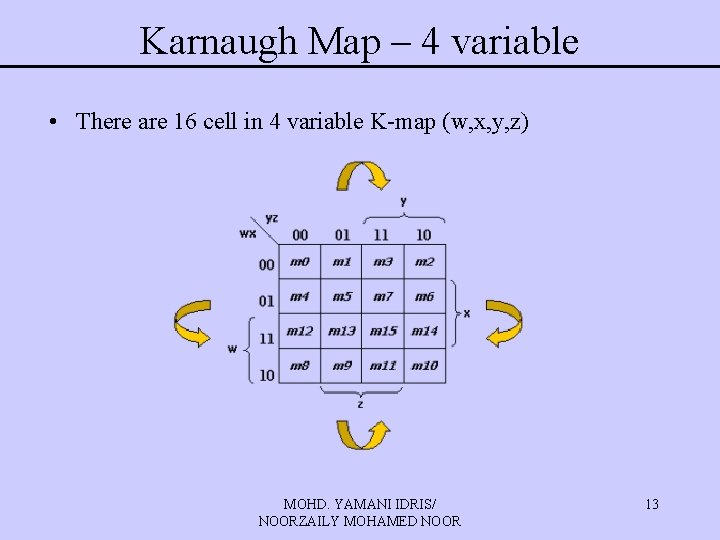
Karnaugh Map – 4 variable • There are 16 cell in 4 variable K-map (w, x, y, z) MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 13

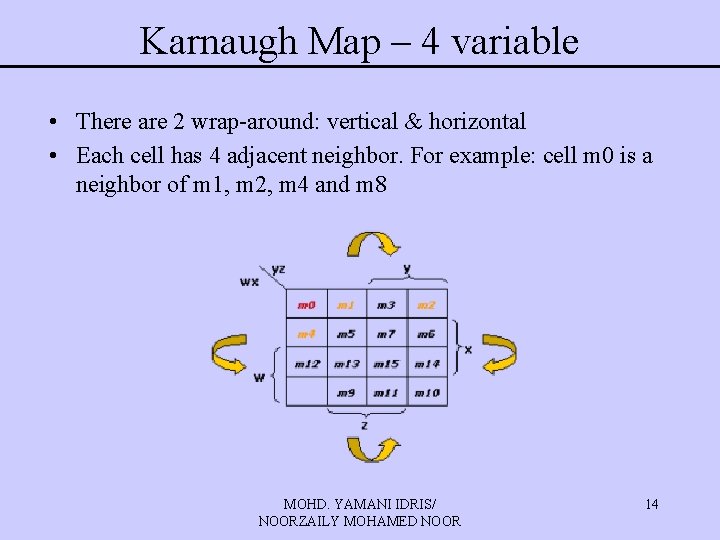
Karnaugh Map – 4 variable • There are 2 wrap-around: vertical & horizontal • Each cell has 4 adjacent neighbor. For example: cell m 0 is a neighbor of m 1, m 2, m 4 and m 8 MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 14

Karnaugh Map – 5 variable • Map for more than 4 variable are more complicated since the geometry (hypercube configuration) for adjacent neighbor is greater. • For five variable; e. g. vwxyz there is 25=32 squares MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 15

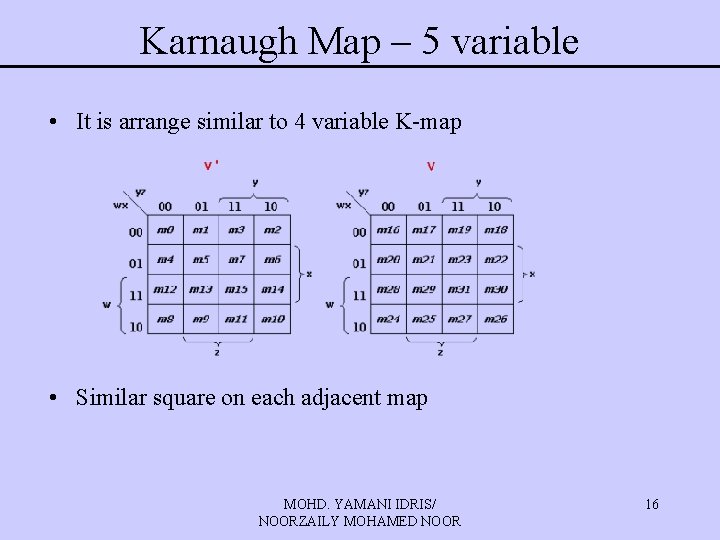
Karnaugh Map – 5 variable • It is arrange similar to 4 variable K-map • Similar square on each adjacent map MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 16

Simplification using Karnaugh Map • Based on Theorem: A+A’=1 • In K-map, each cell contains ‘ 1’ representing minterm for the given function • Each adjacent cell cluster contains ‘ 1’ (the cluster must have a power of two size which is 1, 2, 4, 8…. ) then get the simplified value for each cluster – grouped 2 adjacent squares will eliminate 1 variable, grouped 4 adjacent squares will eliminate 2 variable, grouped 8 adjacent squares will eliminate 3 variable, grouped 2 n adjacent squares will eliminate n variable, MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 17

Simplification using Karnaugh Map • Grouped largest possible squares (minterm) in a cluster – The grater the cluster, the lesser the number of literals in your answer • Get the number of small cluster to gather all squares (minterm) for the function – The lesser the cluster, the lesser the number of ‘product’ and the minimize function MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 18

Simplification using Karnaugh Map • Example: MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 19

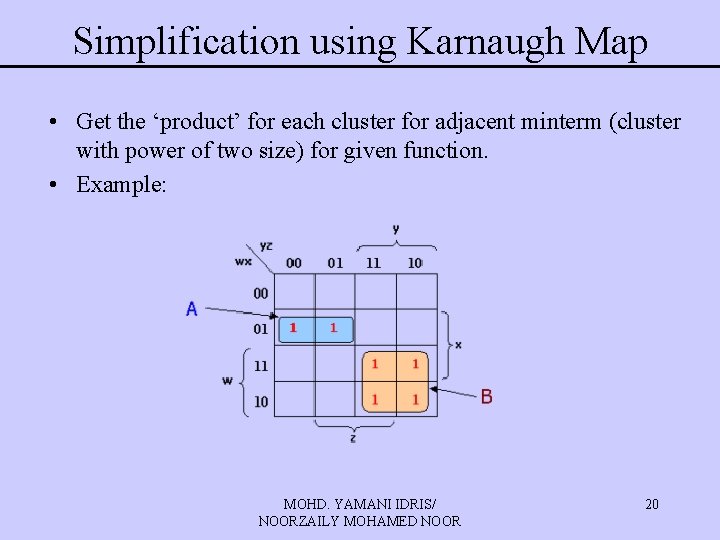
Simplification using Karnaugh Map • Get the ‘product’ for each cluster for adjacent minterm (cluster with power of two size) for given function. • Example: MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 20

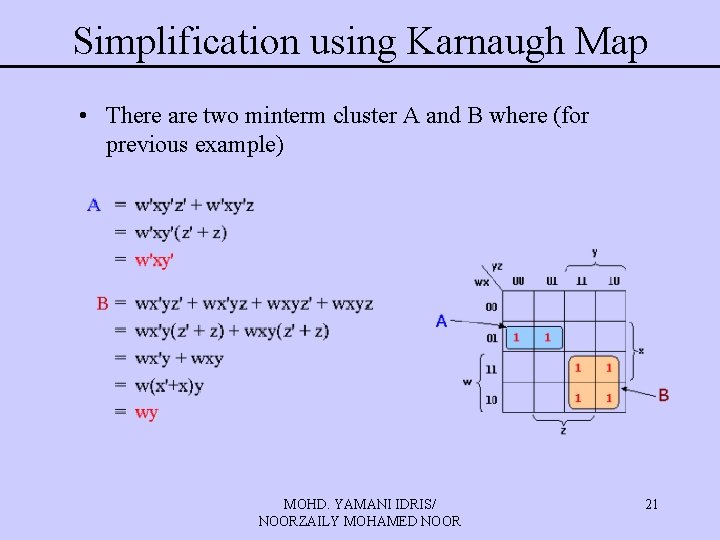
Simplification using Karnaugh Map • There are two minterm cluster A and B where (for previous example) MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 21

Simplification using Karnaugh Map • Each ‘product’ for cluster, w’xy’ and wy represent sumof-minterm in that cluster • Boolean Function is sum-of-product which represent all minterm cluster for that function F(w, x, y, z)=A+B=w’xy’+wy MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 22

Simplification using Karnaugh Map • Greater cluster produce ‘product’ with small number of literal. In 4 variable K-map case: 1 cell = 4 literal, example: wxyz, w’xy’z 2 cell = 3 literal, example: wxy, w’y’z’ 4 cell = 2 literal, example: wx, x’y 8 cell = 1 literal, example: w, y’, z’ 16 cell = no literal example: 1 MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 23

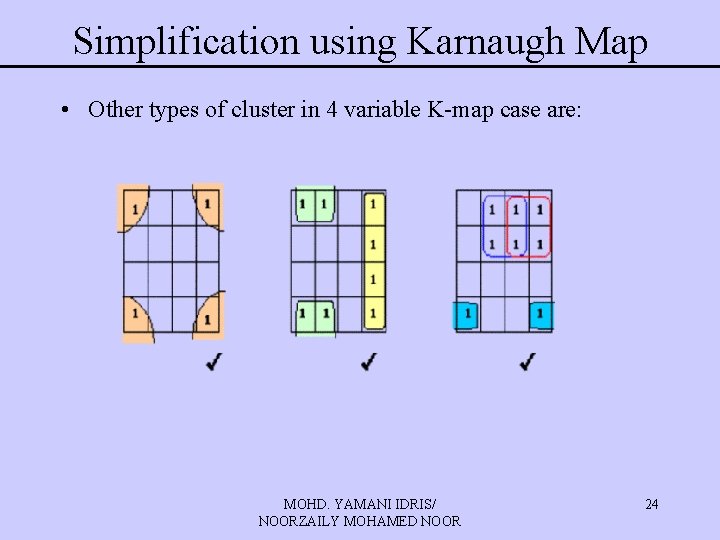
Simplification using Karnaugh Map • Other types of cluster in 4 variable K-map case are: MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 24

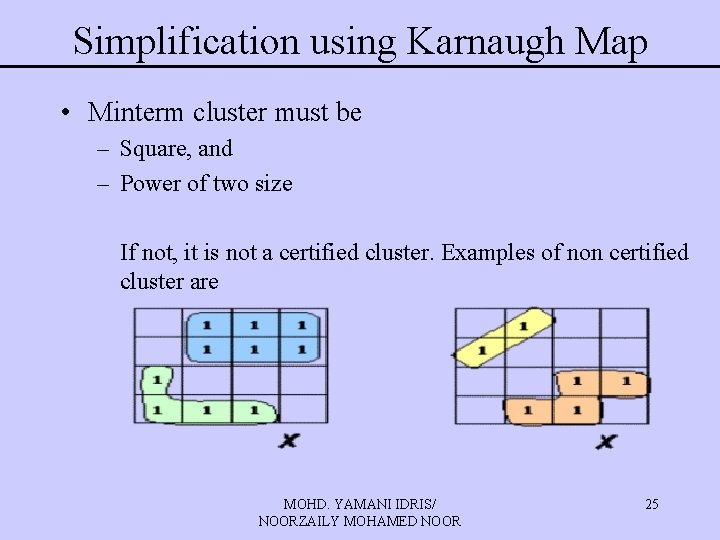
Simplification using Karnaugh Map • Minterm cluster must be – Square, and – Power of two size If not, it is not a certified cluster. Examples of non certified cluster are MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 25

Conversion to Minterm Form • Function is easy to draw in K-map when function is given in SOP or SOM canonical form • How if it is not in sum-of-minterm form? – Convert it to sum-of-product – Elaborate SOP expression to SOM expression, or fill SOP expression directly to K-map MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 26

Conversion to Minterm Form • Example: MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 27

SOP Expression Simplification • To get the simplest SOP expression from K-map, you will need – Minimum number of literal for each ‘product’, and – Minimum number of ‘product’ • This can be achieved in K-map by using – Largest possible number of minterm in one cluster (i. e. prime implicant (PI)) – No extra cluster (i. e. essential prime implicant (epi)) Implicant: is a "covering" (sum term or product term) of one or more in a sum of product (or a maxterm in a product of sum) of a boolean function MOHD. YAMANI IDRIS/ NOORZAILY MOHAMED NOOR 28