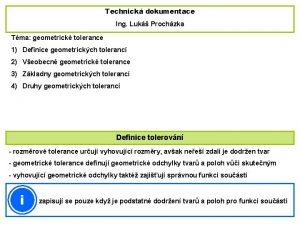
Kapitola K 2 Plochy 1 Plocha je mnoina

Kapitola K 2 Plochy 1

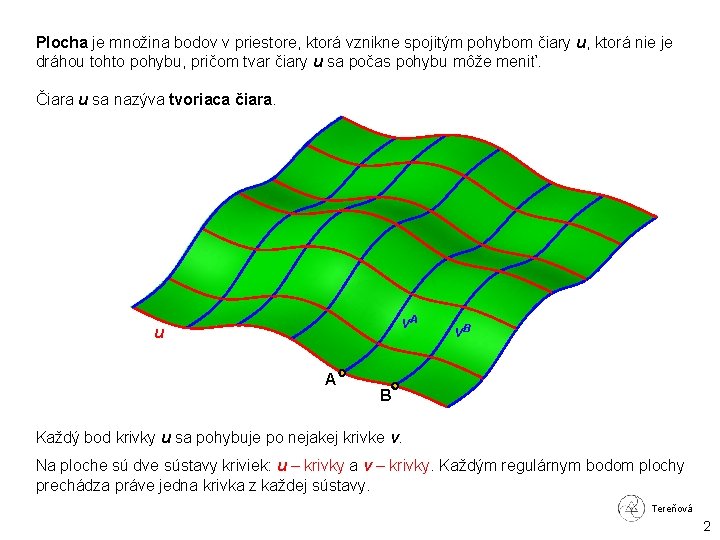
Plocha je množina bodov v priestore, ktorá vznikne spojitým pohybom čiary u, ktorá nie je dráhou tohto pohybu, pričom tvar čiary u sa počas pohybu môže meniť. Čiara u sa nazýva tvoriaca čiara. v. A u A v. B B Každý bod krivky u sa pohybuje po nejakej krivke v. Na ploche sú dve sústavy kriviek: u – krivky a v – krivky. Každým regulárnym bodom plochy prechádza práve jedna krivka z každej sústavy. Tereňová 2

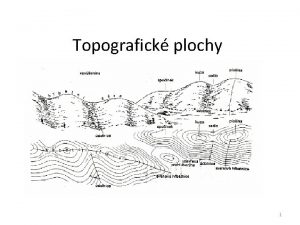
Plochy môžeme rozdeliť na: – empirické (grafické) plochy – sú to plochy, pre ktoré poznáme iba niektoré krivky plochy, zadané napríklad graficky. Príklady: topografické plochy určené sústavou vrstevníc, plochy tvoriace trupy lodí, lietadiel, vodných diel (priehrady) – analytické (geometrické) plochy – sú to plochy, ktoré vieme matematicky zapísať, napr. a) parametricky: x = x(u, v) y = y(u, v) z = z(u, v) u u 1, u 2 , v v 1, v 2 b) implicitne: F(x, y, z) = 0 c) explicitne: z = f(x, y) Príklad: Guľová plocha je analytická plocha. Guľová plocha so stredom S = [0, 0, 0] a polomerom r má vyjadrenie: a) parametrické: x = r. cos(u). cos(v), y = r. cos(u). sin(v), z = r. sin(u), u, v 0, 2 ) b) implicitné: x 2 + y 2 + z 2 - r 2 = 0 c) explicitné: 3

Empirické plochy v diele Franka Gehryho http: //www. cursodehistoriadaarte. com. br/wp-content/uploads/Frank-Gehry-Disney-Concert-Hall-Los-Angeles. . jpg 4

Plochy, ktoré vzniknú pohybom tvoriacej čiary, môžeme rozdeliť podľa typu tvoriacej čiary alebo podľa pohybu a zmeny tvaru tvoriacej čiary. Rozdelenie plôch podľa typu tvoriacej čiary: Priamkové plochy – tvoriaca čiara je priamka. Cyklické plochy – tvoriaca čiara je kružnica. Ostatné plochy – tvoriaca čiara je iného typu. Rozdelenie plôch podľa pohybu a zmeny tvaru tvoriacej čiary: Rotačné plochy – tvoriaca čiara rotuje okolo priamky. Skrutkové plochy – tvoriaca čiara vykonáva skrutkový pohyb. Translačné plochy – tvoriaca čiara sa posúva po inej čiare. Kolineačné, resp. afinné plochy – tvoriaca čiara sa mení pri pohybe tak, že medzi jednotlivými polohami čiary je vzťah kolineácie, resp. afinity. Ostatné plochy – tvoriaca čiara vykonáva iný pohyb. 5

Plochu môžeme vytvoriť nielen pohybom jednej čiary u, ale aj pohybom plochy: Obalové plochy Nech je daná tvoriaca plocha φ. Pohybom tvoriacej plochy φ, ktorá sa pri pohybe môže meniť, vznikne teleso. Jeho hranica (obálka) je obalová plocha Φ. Každá poloha tvoriacej plochy φ sa dotýka obalovej plochy Φ pozdĺž krivky k. Krivka k sa nazýva charakteristika plochy Φ. Každú obalovú plochu môžeme vytvoriť aj pohybom charakteristiky k. Príklad: Anuloid (torus) je obalová plocha, tvoriaca plocha je guľová plocha G, ktorá rotuje okolo priamky o. Každá poloha guľovej plochy sa dotýka anuloidu pozdĺž kružnice k. Anuloid vznikne aj rotáciou kružnice k okolo priamky o. z = o k k x x G y y Tereňová 6

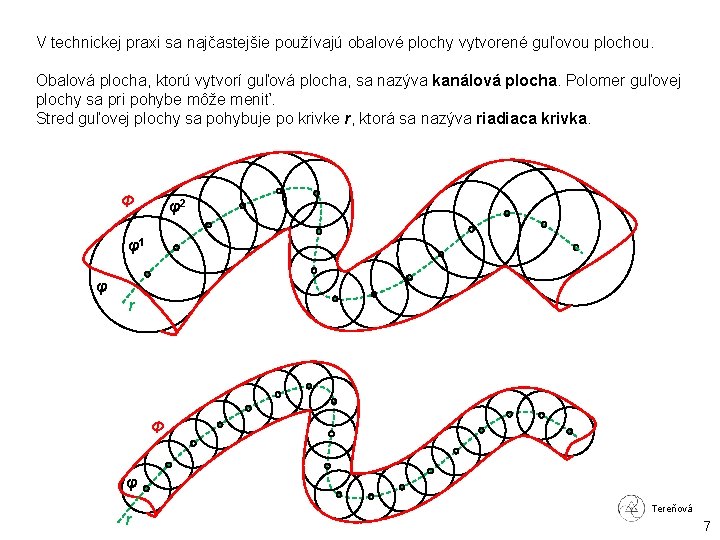
V technickej praxi sa najčastejšie používajú obalové plochy vytvorené guľovou plochou. Obalová plocha, ktorú vytvorí guľová plocha, sa nazýva kanálová plocha. Polomer guľovej plochy sa pri pohybe môže meniť. Stred guľovej plochy sa pohybuje po krivke r, ktorá sa nazýva riadiaca krivka. Φ φ2 φ1 φ r Φ φ r Tereňová 7

Vlastnosti plôch Plocha určená rovnicou F(x, y, z) = 0 s tromi neznámymi, kde F(x, y, z) je polynóm stupňa n, sa nazýva algebrická plocha. Číslo n je stupeň plochy. Geometrický význam stupňa algebrickej plochy: – Každá priamka, ktorá neleží na ploche, pretína algebrickú plochu n-tého stupňa maximálne v n bodoch. – Každá rovina, ktorá nie je časťou plochy, pretína algebrickú plochu n-tého stupňa v krivke, ktorej stupeň je maximálne n. Príklad: Guľová plocha je algebrická plocha 2. stupňa, t. j. kvadratická plocha. Guľová plocha so stredom S = [0, 0, 0] a polomerom r má rovnicu x 2 + y 2 + z 2 - r 2 = 0. Každá priamka pretína guľovú plochu maximálne v 2 bodoch, t. j. – priamka a guľová plocha nemajú žiadny spoločný bod alebo – priamka sa dotýka guľovej plochy, teda má s ňou spoločný jeden bod alebo – priamka má s guľovou plochou dva spoločné body. Ak rovina pretína guľovú plochu, tak rezom guľovej plochy je kružnica, t. j. krivka 2. stupňa. 8

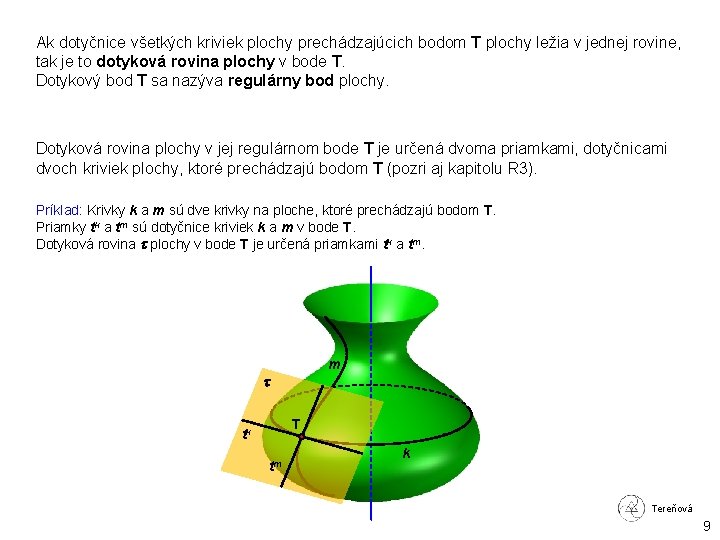
Ak dotyčnice všetkých kriviek plochy prechádzajúcich bodom T plochy ležia v jednej rovine, tak je to dotyková rovina plochy v bode T. Dotykový bod T sa nazýva regulárny bod plochy. Dotyková rovina plochy v jej regulárnom bode T je určená dvoma priamkami, dotyčnicami dvoch kriviek plochy, ktoré prechádzajú bodom T (pozri aj kapitolu R 3). Príklad: Krivky k a m sú dve krivky na ploche, ktoré prechádzajú bodom T. Priamky tk a tm sú dotyčnice kriviek k a m v bode T. Dotyková rovina plochy v bode T je určená priamkami tk a tm. m T tk tm k Tereňová 9

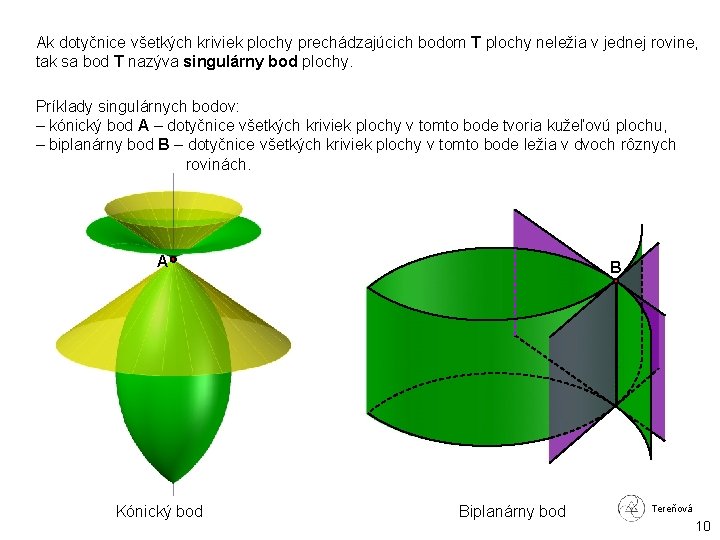
Ak dotyčnice všetkých kriviek plochy prechádzajúcich bodom T plochy neležia v jednej rovine, tak sa bod T nazýva singulárny bod plochy. Príklady singulárnych bodov: – kónický bod A – dotyčnice všetkých kriviek plochy v tomto bode tvoria kužeľovú plochu, – biplanárny bod B – dotyčnice všetkých kriviek plochy v tomto bode ležia v dvoch rôznych rovinách. A Kónický bod B Biplanárny bod Tereňová 10

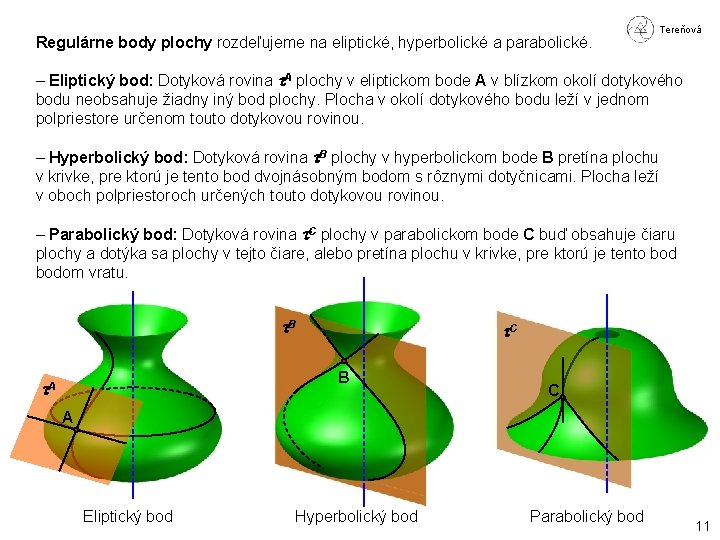
Regulárne body plochy rozdeľujeme na eliptické, hyperbolické a parabolické. Tereňová – Eliptický bod: Dotyková rovina A plochy v eliptickom bode A v blízkom okolí dotykového bodu neobsahuje žiadny iný bod plochy. Plocha v okolí dotykového bodu leží v jednom polpriestore určenom touto dotykovou rovinou. – Hyperbolický bod: Dotyková rovina B plochy v hyperbolickom bode B pretína plochu v krivke, pre ktorú je tento bod dvojnásobným bodom s rôznymi dotyčnicami. Plocha leží v oboch polpriestoroch určených touto dotykovou rovinou. – Parabolický bod: Dotyková rovina C plochy v parabolickom bode C buď obsahuje čiaru plochy a dotýka sa plochy v tejto čiare, alebo pretína plochu v krivke, pre ktorú je tento bodom vratu. B C B A C A Eliptický bod Hyperbolický bod Parabolický bod 11

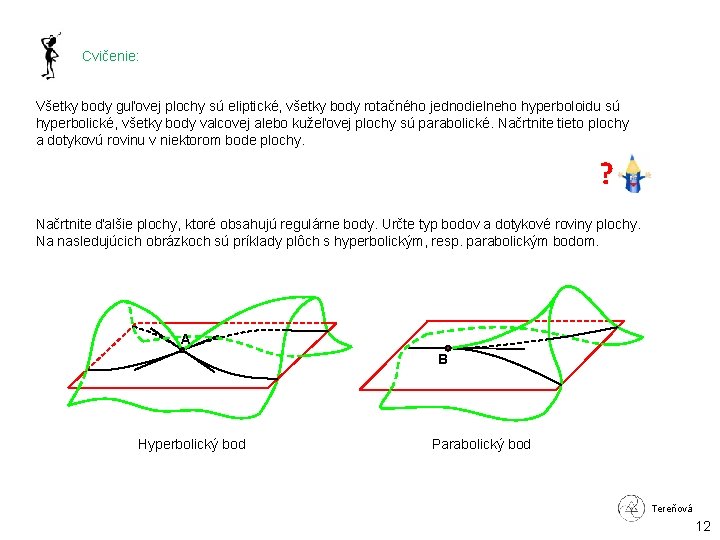
Cvičenie: Všetky body guľovej plochy sú eliptické, všetky body rotačného jednodielneho hyperboloidu sú hyperbolické, všetky body valcovej alebo kužeľovej plochy sú parabolické. Načrtnite tieto plochy a dotykovú rovinu v niektorom bode plochy. ? Načrtnite ďalšie plochy, ktoré obsahujú regulárne body. Určte typ bodov a dotykové roviny plochy. Na nasledujúcich obrázkoch sú príklady plôch s hyperbolickým, resp. parabolickým bodom. A B Hyperbolický bod Parabolický bod Tereňová 12

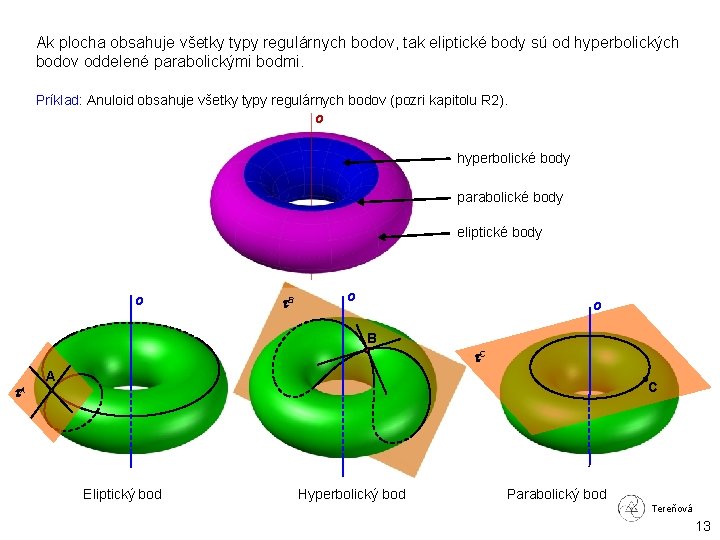
Ak plocha obsahuje všetky typy regulárnych bodov, tak eliptické body sú od hyperbolických bodov oddelené parabolickými bodmi. Príklad: Anuloid obsahuje všetky typy regulárnych bodov (pozri kapitolu R 2). o hyperbolické body parabolické body eliptické body o B o o B C A C A Eliptický bod Hyperbolický bod Parabolický bod Tereňová 13

Dotyk dvoch plôch: Dve plochy sa dotýkajú pozdĺž spoločnej krivky k, ak sa dotýkajú v každom bode tejto krivky, t. j. v každom bode krivky k majú spoločnú dotykovú rovinu. k Torzálna priamka plochy je taká priamka na ploche, pre ktorú vo všetkých jej bodoch existuje jediná spoločná dotyková rovina plochy. p Príklad: Na obrázku je zobrazená tvoriaca priamka p valcovej plochy. Je to torzálna priamka a dotyková rovina v každom jej bode je rovina . Tereňová 14

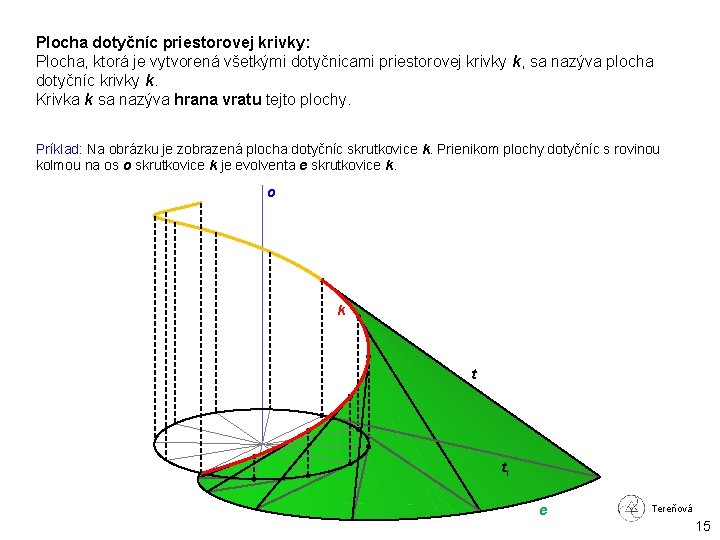
Plocha dotyčníc priestorovej krivky: Plocha, ktorá je vytvorená všetkými dotyčnicami priestorovej krivky k, sa nazýva plocha dotyčníc krivky k. Krivka k sa nazýva hrana vratu tejto plochy. Príklad: Na obrázku je zobrazená plocha dotyčníc skrutkovice k. Prienikom plochy dotyčníc s rovinou kolmou na os o skrutkovice k je evolventa e skrutkovice k. o k t t 1 e Tereňová 15

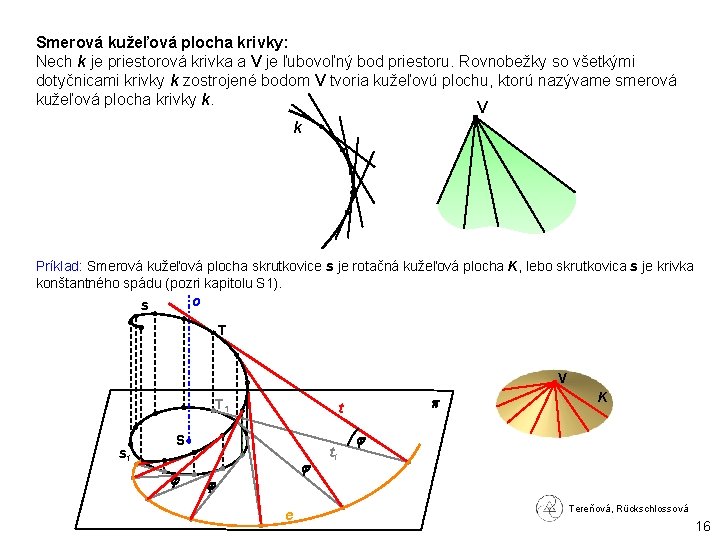
Smerová kužeľová plocha krivky: Nech k je priestorová krivka a V je ľubovoľný bod priestoru. Rovnobežky so všetkými dotyčnicami krivky k zostrojené bodom V tvoria kužeľovú plochu, ktorú nazývame smerová kužeľová plocha krivky k. V k Príklad: Smerová kužeľová plocha skrutkovice s je rotačná kužeľová plocha K, lebo skrutkovica s je krivka konštantného spádu (pozri kapitolu S 1). o s T V T 1 s 1 S t e t 1 K Tereňová, Rückschlossová 16

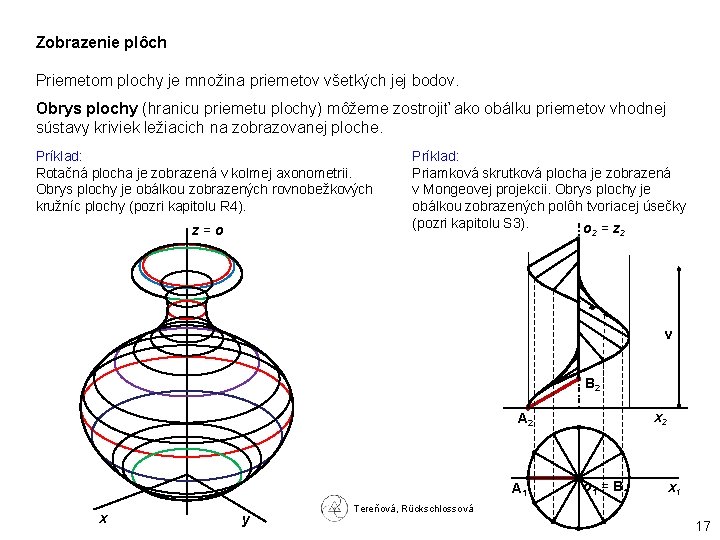
Zobrazenie plôch Priemetom plochy je množina priemetov všetkých jej bodov. Obrys plochy (hranicu priemetu plochy) môžeme zostrojiť ako obálku priemetov vhodnej sústavy kriviek ležiacich na zobrazovanej ploche. Príklad: Rotačná plocha je zobrazená v kolmej axonometrii. Obrys plochy je obálkou zobrazených rovnobežkových kružníc plochy (pozri kapitolu R 4). z = o Príklad: Priamková skrutková plocha je zobrazená v Mongeovej projekcii. Obrys plochy je obálkou zobrazených polôh tvoriacej úsečky (pozri kapitolu S 3). o = z 2 2 v B 2 x 2 A 1 x y o 1 = B 1 x 1 Tereňová, Rückschlossová 17