Kapitel 8 Graphalgorithmen 8 1 8 2 8

Kapitel 8: Graphalgorithmen 8. 1 8. 2 8. 3 8. 4 8. 5 8. 6 Grundlagen Tiefen- und Breitensuche Prim- und Kruskal-Algorithmus Kürzeste Wege in Graphen Eulersche und Hamiltonsche Graphen Bipartite Graphen 1

8 Algoritmos sobre grafos 8. 1 Conceptos básicos Definiciones Grafo dirigido (Digraph): un par ordenado G = (V, E) , donde V = un conjunto de nodos (finito en la mayoría), E = un conjunto de arcos, subconjunto de V V. (los arcos tienen una dirección!) 2

Definición (2) w se llama sucesor de v yv predecesor de w, cuando hay un (v, w) de E. Loop = arco(v, v). 4

Grafo (no dirigido) Los arcos no tienen dirección! Formalmente: un par ordenado G = (V, E) , donde V = conjunto de nodos (casi siempre finito), E = conjunto de arcos, un multiconjunto de pares no ordenados de V. (se admiten multiples arcos entre nodos!) Un grafo se llama simple cuando no tiene multiples arcos ni loops. 5

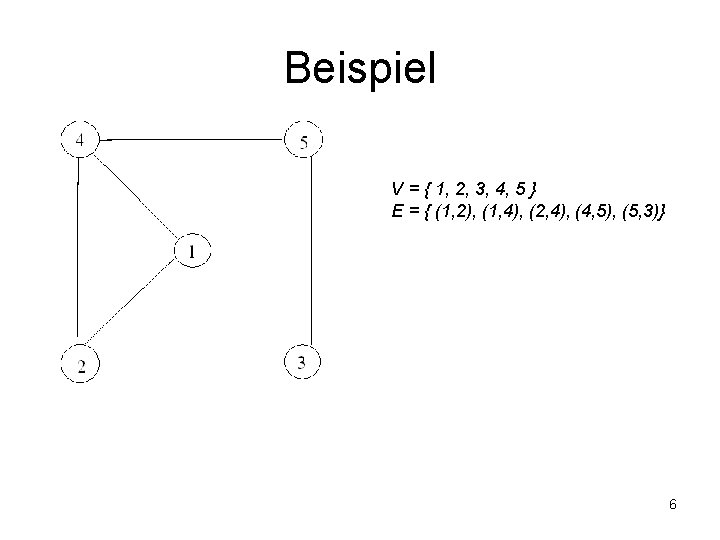
Beispiel V = { 1, 2, 3, 4, 5 } E = { (1, 2), (1, 4), (2, 4), (4, 5), (5, 3)} 6

Grafo con pesos Es un Grafo con arcos valorados : tripleta G = (V, E, d) mit (V, E): Grafo d: E {x R | x 0} valoración de arcos 7

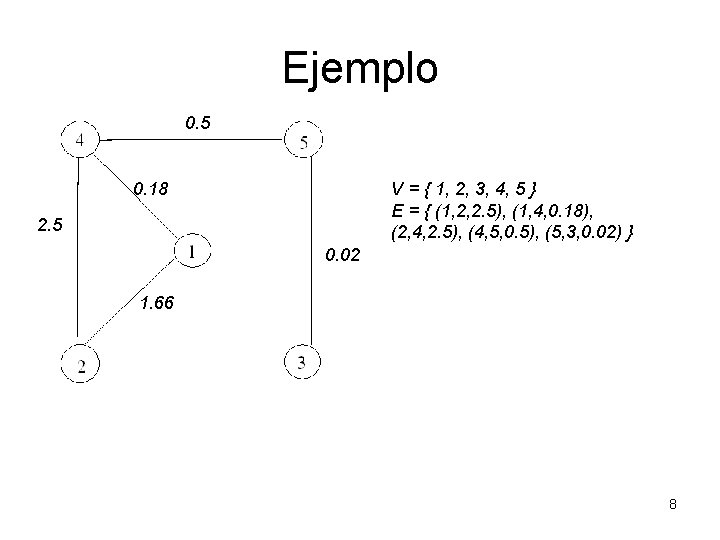
Ejemplo 0. 5 0. 18 V = { 1, 2, 3, 4, 5 } E = { (1, 2, 2. 5), (1, 4, 0. 18), (2, 4, 2. 5), (4, 5, 0. 5), (5, 3, 0. 02) } 2. 5 0. 02 1. 66 8

Grado de los vértices Sea v un nodo en un grafo no dirigido. Grado del vértice g(v) : = número arcos que inciden en v = número de arcos que tienen un extremo en v. Lema: Sea G grafo no dirigido sin loops. Entonces {v V} g(v) es un número par. En un grafo dirigido: Grado de arcos salientes/entrantes de un nodo v : = número de arcos que empiezan/terminan en v 9

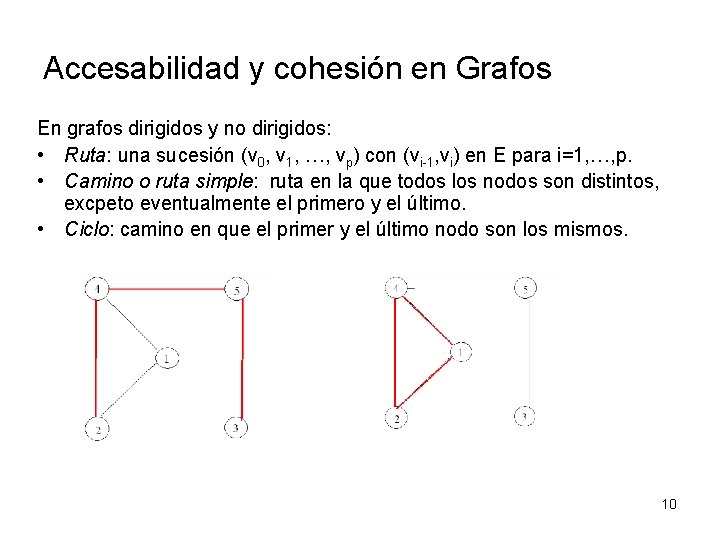
Accesabilidad y cohesión en Grafos En grafos dirigidos y no dirigidos: • Ruta: una sucesión (v 0, v 1, …, vp) con (vi-1, vi) en E para i=1, …, p. • Camino o ruta simple: ruta en la que todos los nodos son distintos, excpeto eventualmente el primero y el último. • Ciclo: camino en que el primer y el último nodo son los mismos. 10

Definiciones (3) En un grafo no dirigido • Los nodos v y w están conectados o w se puede alcanzar desde v si hay un un camino de v hasta w. • Un Subgrafo de un grafo G=(V, E) es un grafo G´=(V´, E´) tal que: V´ subconjunto de V y E´ Subconjunto de E. • El subgrafo compuesto por todos los nodos alcanzables desde w y todos los arcos entre estos nodos se llama componente conexa de w. • Si este corresponde a todo el grafo (y por lo tanto es independiente de w) se dice que el grafo es conexo. • Un grafo conexo sin ciclos es un árbol. 11

Definiciones (4) Analogamente en un grafo dirigido: • Dos nodos v y w se dices fuertemente relacionados cuando hay un camino de v a w y un camino de w a v gibt. • Una compoenente fuertemente conexa es un subgrafo con el número máximo de arcos posibles. Es decir, de un nodo cualquiera salen (y llegan) arcos a todos los otros nodos. 12

Ejemplos de Grafos: • • Red de tráfico con caminos y cruces. Redes de cañerías Flujos: grafos dirigidos Redes de computadores (transmisión de datos) Largos o costos y capacidades de los arcos se representan por pesos, y/o valores en los arcos. 13

Problemas importantes en la tería de grafos • Calcular la distancia mínima desde un nodo de salida hasta todos los otros nodos. • Calcular un árbol cobertor (el subgrafo que tiene la menor suma de la cantidad/costo/largo de los arcos que une a todos los nodos). • Encontrar un elemento en el grafo, determinar si hay ciclos. • Cálculo de un camino que pasa justo una sola vez por todos los arcos/nodos. • Coloracion de grafos. • Centralidades en grafos: ej. Cual es el nodo mas „central“. 14

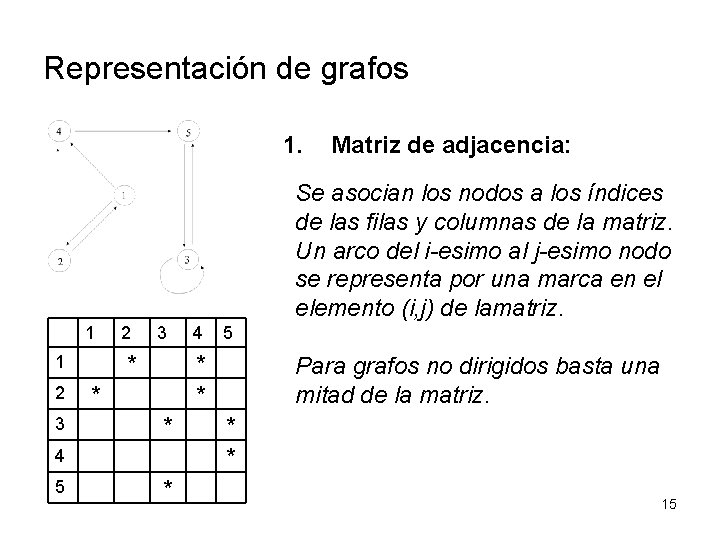
Representación de grafos 1. Matriz de adjacencia: Se asocian los nodos a los índices de las filas y columnas de la matriz. Un arco del i-esimo al j-esimo nodo se representa por una marca en el elemento (i, j) de lamatriz. 1 1 2 3 * 5 * * Para grafos no dirigidos basta una mitad de la matriz. * * 4 5 4 * * * 15

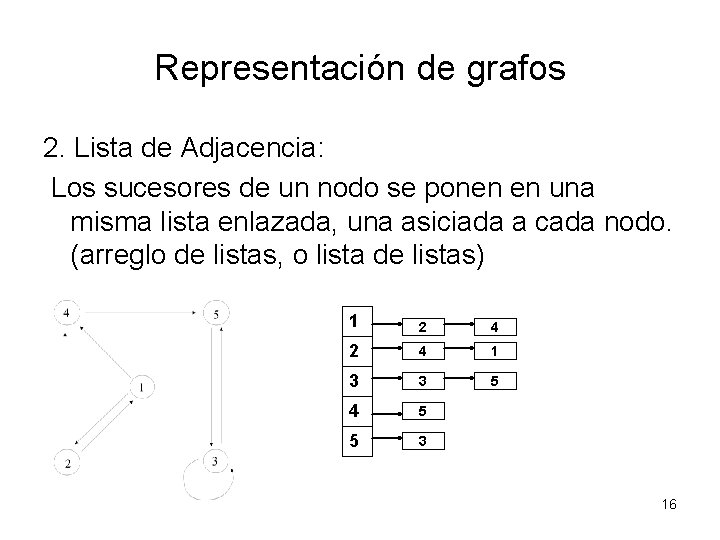
Representación de grafos 2. Lista de Adjacencia: Los sucesores de un nodo se ponen en una misma lista enlazada, una asiciada a cada nodo. (arreglo de listas, o lista de listas) 1 2 4 1 3 3 5 4 5 5 3 16

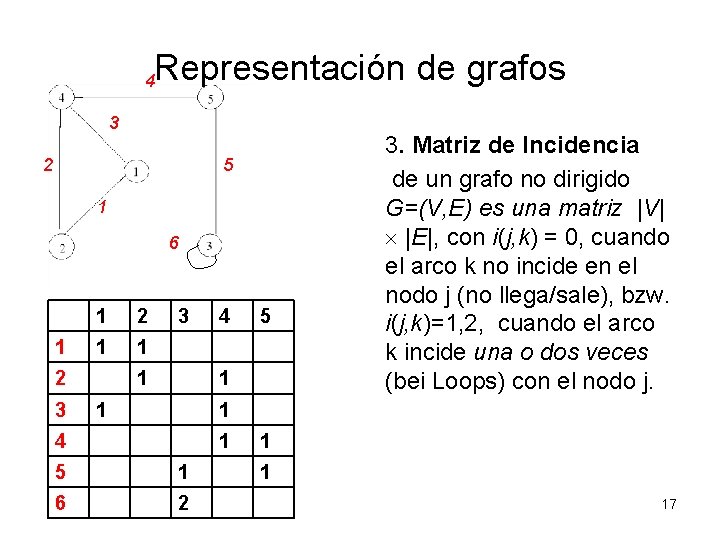
Representación de grafos 4 3 2 5 1 6 1 1 2 3 3 1 4 5 1 1 3. Matriz de Incidencia de un grafo no dirigido G=(V, E) es una matriz |V| |E|, con i(j, k) = 0, cuando el arco k no incide en el nodo j (no llega/sale), bzw. i(j, k)=1, 2, cuando el arco k incide una o dos veces (bei Loops) con el nodo j. 1 4 1 5 1 6 2 1 1 17

Costo de las representaciones 1. Matriz de adjacencia Memoria: O(|V|²) costo de saber si hay un arco (v, w): O(1). 2. Lista de adjacencia Memoria: O(|V|+|E|) costo de saber si hay un arco (v, w): O(|E|). 3. Matriz de incidencia Memoria: O(|V| • |E|) 18

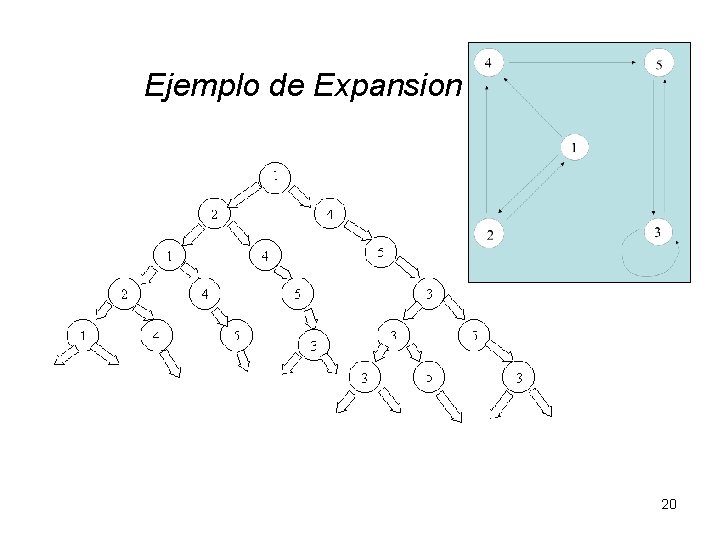
8. 2 Búsqueda (recorrido) en profundidad o en amplitud La expansión de un grafo dirigido desde un nodo v se representa por un árbol X(v) donde: • X(v) = (v), si v no tiene sucesores, • X(v) = (v, X(v 1), …, X(vp)), si v 1, …, vp son los sucesores de v. Cuando el grafo tiene ciclos la expansión es infinitamente. 19

Ejemplo de Expansion 20

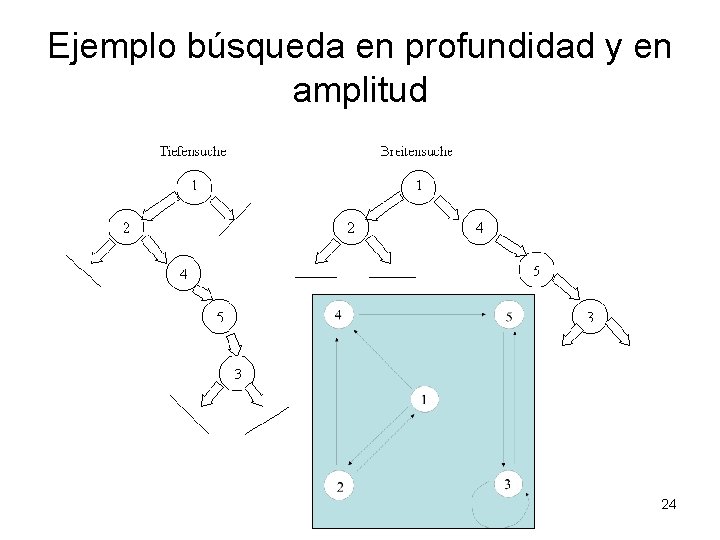
Dos algoritmos de búsqueda En profundidad: en un grafo dirigido G hacer un recorrido similar al de preorden (primero los hijos luego el padre) pero se detiene la recursividad cuando se alcanza un einem gerichteten Graphen G: Preorder-Durchlauf der Expansion von G mit Abbruch jeweils bei einem schon besuchten Knoten des Graphen: rekursiv: Profundidad(v) si v no ha sido visitado: procesar v; marcar v como visitado; para todo sucesor de N(v) de v (de izquierda a derecha) invocar (N(v)). costo: O(|V| + |E|). Estructura de datos: Stack. 21

Búsqueda en amplitud Procesar en expansión primero la raíz, luego los nodos en nivel 1, luego nodos en nivel 2, usw. costo: O(|V| + |E|). Estructura d edatos: Queue 22

Algoritmo Búsqueda en amplitud print(root) Mark(root) p = new Queue() put all neighbors of root in q and mark them while(!empty(q)) { o = dequeue(q) print(o) put all not marked neighbors of o in q and mark them } • 23

Ejemplo búsqueda en profundidad y en amplitud 24

8. 3 Algoritmos de Prim- y Kruskal Recordemos: un grafo conexo (no dirigido ) zin ciclos es un árbol. Características: • Tiene n nodos y exactamente n-1 arcos. • Si se le pone un arco más entonces se crea un ciclo en el grafo. Objetivo: Calcular el spanning tree de minimo costo para un grafo conexo no dirigido (un árbol que es subgrafo del original que contiene todos los nodos y la suma de los costos de sus arcos es mínima). 25

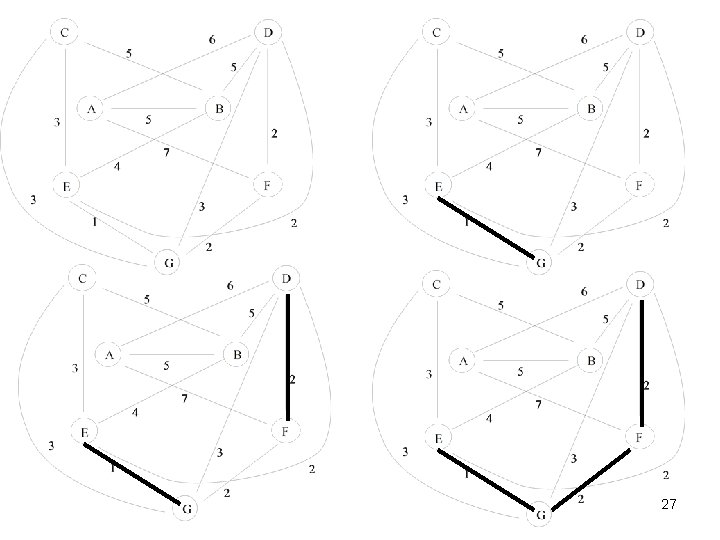
Algoritmo de Kruskal Descripción: • Descomponer el grafo y su conjunto de nodos en componentes unitarias en una particion P de una estructura tipño Find-and-Merge. • Los arcos se ordenan segun sus costos de menor a mayor usando una cola de prioridad Q: Si el arco de menor costo une dos componentes de la estructura se usa para la construcción del spanning tree minimal T. Las componentes que une se funden entonces en una sola. Si no se ignora. • Cuando la estructura quede con una componente entonces esta corresponde al spanning tree T de G. 26

27

Sea G=(V, E, d) un grafo conexto con n nodos. Sea e : = |E|. Algorithmus Kruskal (G) //Computa el spanning tree minimal de G Inicializar la partición P de modo que cada nodo V es una componente # O(n) Sea T = (V, { }); Construir una cola de prioridad (Heap) Q con los arco # O(e log e) ncomp : = n; while ncomp > 1 do # máximo e iteraciones (Q, (v, w)) : = deletemin(Q); # O(log e) a: = find (P, v); # O(log n) b: = find (P, w); # O(log n) if a!=b {insert(T, (v, w)) ; P: = merge(P, a, b); dec(ncomp); } # O(1) end {Kruskal}. Partition in Find-and-Merge-Struktur: con ella se construye el spanning tree. Costo total : O(e log e) (Notar: e >= n-1, ya que el grafo es conexo). 29

Correctitud del algoritmo de Kruskal: Por probar: el árbol construido T es minimal. Prueba por contradicción. Suposición: no es el caso. Sea H un árbol cobertor minimal, que tiene los arcos casi todos coincidentes con T. Sea ei el primer arco considerado por el algoritmo que solo pertenece a E(T) o solo pertenece a E(H), pero no está en ambos. Segun el algoritmo el segundo caso (esta en E(H), pero no en E(T)) imposible. Por lo tanto, ei esta en E(T), pero no en E(H). Si uno pone ei en el árbol H entonces se tiene en „H con ei “ un ciclo. En este ciclo hay un arco em, que no pertenece a T. Si lo sacamos entonces tenemos un nuevo árbol cobertor H‚ que tiene a lo más el mismo peso que H. Según la definición de ei éste se considera antes que em por el algoritmo, o sea puede tener a lo más el mismo peso que em. Con esto es H´ también un árbol cobertor mínimo y tiene un un arco más en común con T 30

Algoritmo de Prim Sea G=(V, E, d) un grafo conexo con pesos. Objetivo: calcular el árbol cobertor mínimo T. Breve: Construir el árbol T por pasos: Partir con un vértico (nodo) cualquiera. incorporar siempre el arco con menor peso (costo) que tiene un extremo en el árbol construido y otro fuera de él hasta que todos los nodos hayan sido incorporados al árbol. 31

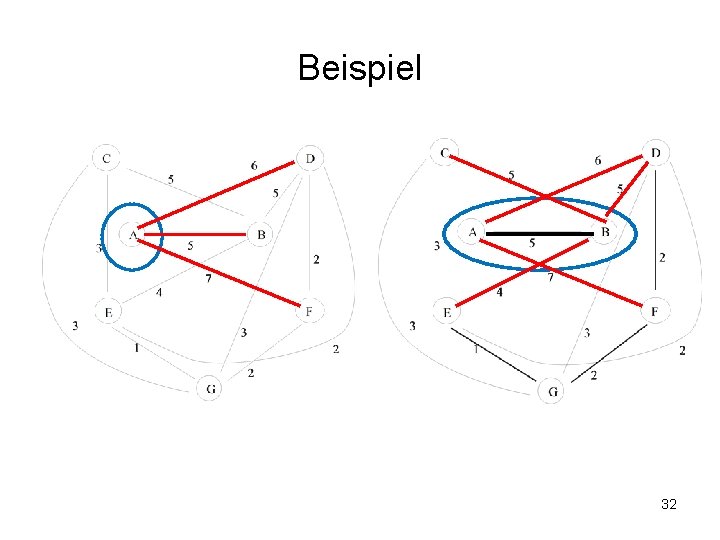
Beispiel 32

Algoritmo de Prim - detallado Construir: • Lista de n vértices, en la que se especifican sus respectivos arcos con sus pesos y su posición en el heap (de los arcos), • Lista de arcos con sus vértices. § Inicializar dos conjuntos de nodos M = { } y N=V M así como el árbol cobertor T = (V, { }). § Escoger un vértice y 0 de V, poner M: ={y 0} y adaptar N. § Definir s(y) : = d(y, y 0), donde d(y) = max. Integer, si es que no hay un arco entre y 0 a y. § Se construye un Heap (según la función: s(y)) de todos los arcos que salen de N se guarda su posición en el Heap en la lista de vértices. WHILE N <> { } DO BEGIN § Sea y 1 el nodo con el s(y 1) mínimo. Se inserta el arco de M a y 1 en T, se saca y 1 del Heap y se pone y 1 en M. § Redefinir s(y) : = min {s(y), d(y 1, y)} para todo y de N. § Ahora debe adecuarse el heap para todos los sucesores de y 1. Esto puede ser realizado con la informacion de ka posición en el Heap con un costo de O(log n). END # While 34

Costo del Algoritmo de Prim: • Construir la lista de vértices y el primer Heap: O(|E| + |V| log |V|) (O usando la idea de que un heap puede construirse en tiempo lineal: O(|E| + |V|) = O(|E|) ). • La actualización del heap requiere que se itere sobre la lista de los sucesores de un vértice: costo = O(|E| log |V|), es decir O(log |V|) por cada sucesor. • La readecuación del Heap se tiene que hacer la cantidad de vértices que hayan |V|-veces, cada vez que se extrae el mínimo. costo: O(|V| log |V|). Costo total: O(|E| log|V|) (ya que |E| |V|-1) 35

Bases para el Algoritmo de Prim: Observación: Loa árboles de cobertura mínimos tienen siempre un arco con el peso mínimo. Demostración: Si no fuera así se puede introducir este arco y se creará un ciclo. Como dos vértices pueden alcanzarse uno a otro por dos caminos distintos, basta borrar uno sin que deje de ser un árbol conexo. De esta manera se puede lograr otro árbol que tiene al menos el mismo peso que el original (sino menor). 36

Esta característica es válida en forma más general aún. Sean U y W una partición del conjunto de vértices de G en dos subconjuntos disjuntivos y (u, w) un arco de costo mínimo que une estos dos conjuntos. Entonces existe un árboil de costo mínimo que contiene este arco. Demostración: aquí también se podria incluir (u, w) y borrar otro arco (u', w') que une U con W. La correctitud del algoritmo se demuestra ya que la última observación se aplica en cada iteración del algoritmo para unir los conjuntos de los nodos que están en el árbol construido hasta ahora con los nodos del conjunto de vértices que aún no están 37

8. 4 Distancias mínimas en Grafos „Single source shortest path problem“ Dado: • Grafo dirigido con pesos (todos 0), • Un vértice („pubto de partida“) v 0 en el grafo. Buscar: camino más corto de v 0 a todos los otros nodos (suponiendo que hay camino a ellos). 38

Dijkstra-Algorithmus Dijkstra (v 0, G) //verdes; distancia final calculada, amarillos distancia previa calculada para todo u { dist(u) : = maxint }; verde : =vacío; amarillo: = {v 0}; dist(v 0): =0; While amarillo != vacío do { escoger w de amarillo de modo que dist(w) minimal; colorear w verde; para cada u scc(w) do { si u está en V(verde o amarillo) { colorear u amarillo; dist(u): = dist(w)+ cost(w, u); } si u de amarillo //tenia calculada una distancia preliminar { si dist (u) > dist(w)+cost(w, u) entonces dist(u): =dist(w)+cost(w, u) } } } end; 39

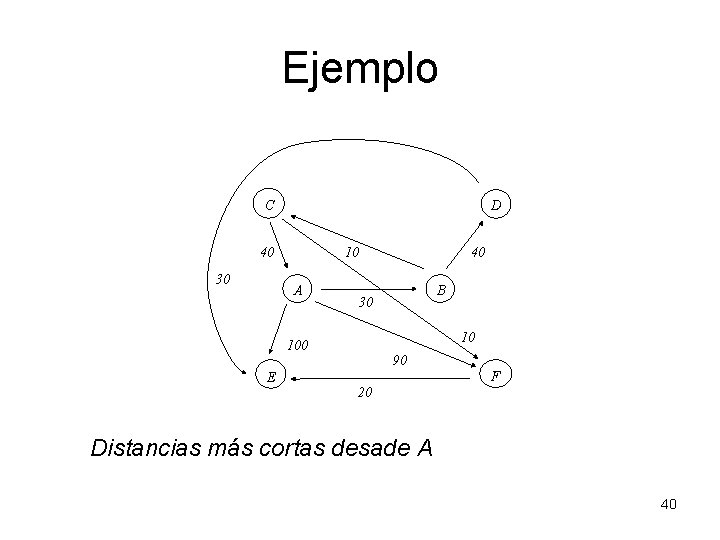
Ejemplo C D 40 30 40 10 A 10 100 E B 30 90 F 20 Distancias más cortas desade A 40

Descripción: Idea: Hacer crecer el subárbol construido hasta ahora por los caminos más cortos. Nodos verdes: nodos cuyos sucesores ya han sido considerados. = nodos a los cuales ya se les ha calculado la distancia mínima. Nodos amarillos: los sucesores de los nodos verdes que no son verdes Arcos rojos: arcos sobre los cuales pasa al menos una ruta óptima de las calculadas hasta el momento. Arcos amarillo: arcos que han sido reconocidos como no optimales. 41

Ciclo Un ciclo del algoritmo: • De todos los nodos amarillos, colorear verde el w el que tiene menor distancia a v 0. • Colorear amarillo todos los sucesores de w. • Registrar o corregir los caminos más cortos desde v 0 a cada uno de los sucesores de w, asi como su longitud (con esto arcos no coloreados pueden tornarse rojos y arcos rojos pueden tornarse amarillos). 42

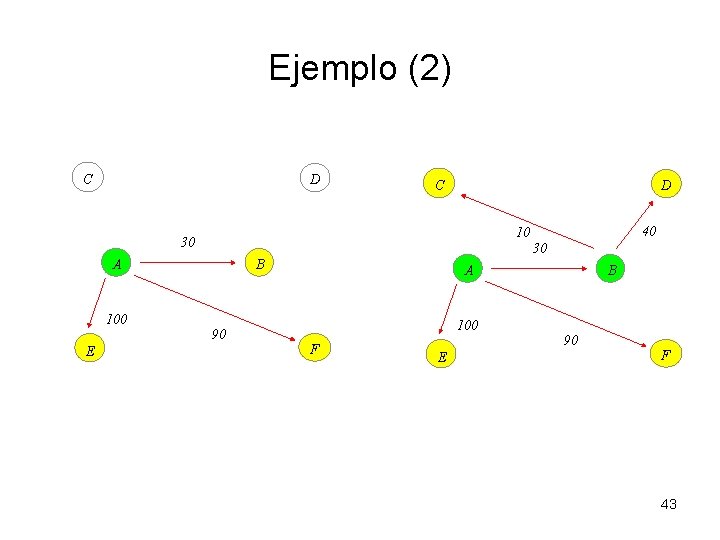
Ejemplo (2) C D 30 A 100 E 40 10 30 B A 100 90 F E B 90 F 43

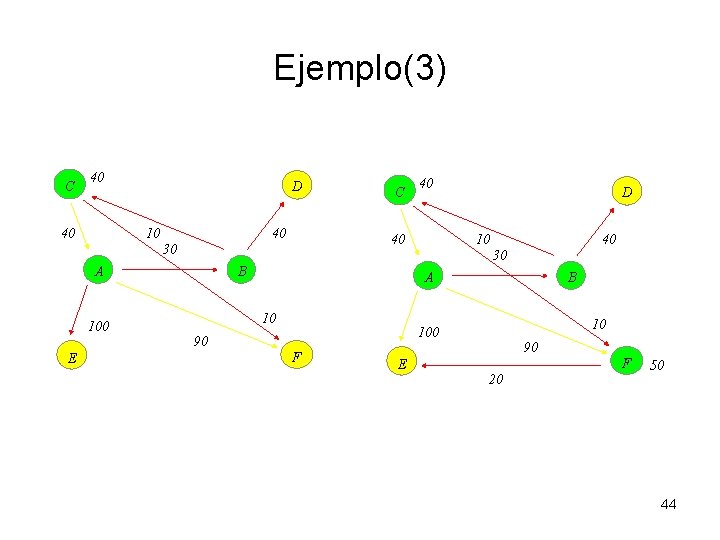
Ejemplo(3) C 40 40 D 40 10 30 A E 40 40 30 100 C B A 10 B 10 100 90 F E 90 F 20 50 44

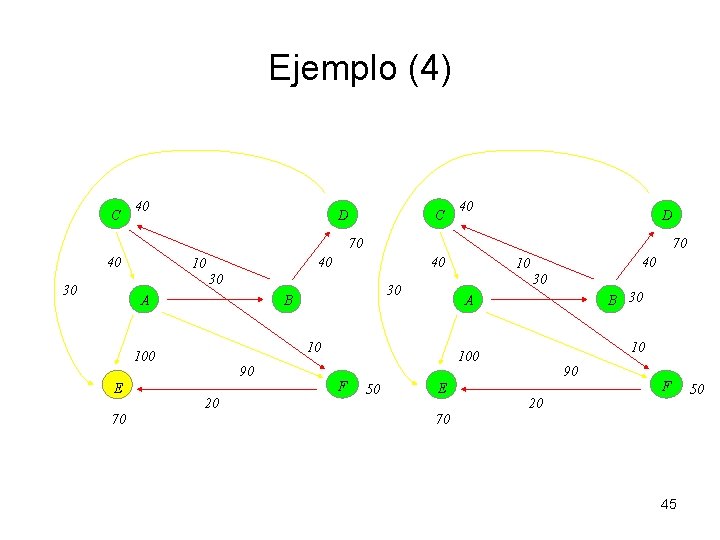
Ejemplo (4) C 40 D 70 40 10 40 30 30 A 70 10 100 90 F 20 B 30 A 10 100 E 30 30 B 40 10 50 E 90 F 20 70 45 50

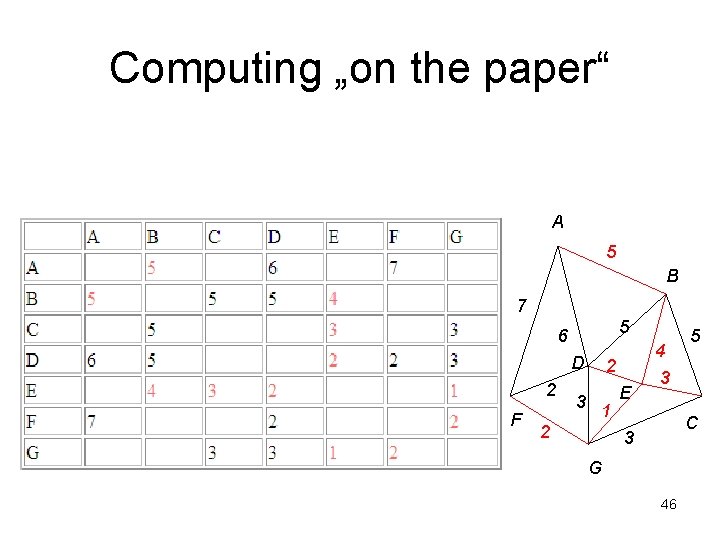
Computing „on the paper“ A 5 B 7 5 6 D 2 F 3 2 1 2 E 4 3 5 C 3 G 46

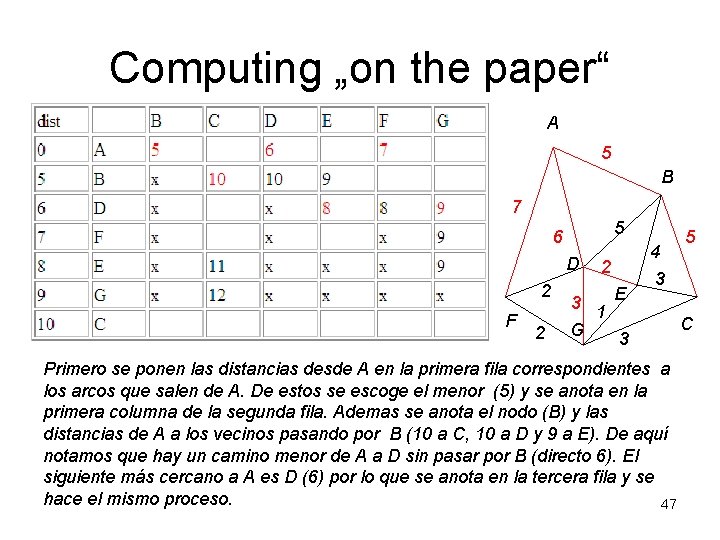
Computing „on the paper“ A 5 B 7 5 6 D 2 F 2 2 E 3 1 G 3 4 3 Primero se ponen las distancias desde A en la primera fila correspondientes a los arcos que salen de A. De estos se escoge el menor (5) y se anota en la primera columna de la segunda fila. Ademas se anota el nodo (B) y las distancias de A a los vecinos pasando por B (10 a C, 10 a D y 9 a E). De aquí notamos que hay un camino menor de A a D sin pasar por B (directo 6). El siguiente más cercano a A es D (6) por lo que se anota en la tercera fila y se hace el mismo proceso. 47 5 C

8. 4. 2 Implementación del Algoritmo a) Implementación con una matriz de adjacencia Sea V={1, . . . , n} y sea cost(i, j) la matriz de distancias donde se registra un infinito donde no hay camino directo entre dos nodos. Además usaremos: double dist[] = new double[n]; node father[] = new node[n]; boolean green[] = new boolean[n]; El arreglo father representa el árbol de los arcos rojos, en el cual cada nodo apunta a su nodo padre. Los nodos amarillo no se representan explícitamente. 48

Ciclo Cada iteración consta de los siguientes pasos: • El arreglo dist se recorre completo, para encontrar el w amarillo con la menor distancia. costo: O(n). • Las lineas cost(w, *) de la matriz son recorridas para corregir (en caso necesario) las distancias de los sucesores de w. costo: O(n). Costo total: O(n²), ya que hay n iteraciones. Inefficiente, salvo cuando n es muy chico o e cercano a n² ! 49

b) Implemntaciòn con listas de adyacencia y Heap Grafo: dado con listas de adjacencia. Como antes: • Array dist • Array father Además: • Heap (implementado cmo arreglo) de todos los nodos amarillos, ordenados según distancia al nodo de origen, • Array heapaddress, que contiene para cada nodo amarillo su posición en el Heap. 50

Iteración Cada iteraci+on consta de los siguientes pasos: 1. Sacar el nodo amarillo w con la distancia mínima del Heap Aufwand: O(log n). 2. Encontrar en la lista de adyacencia m(w) sucesor de w. Aufwand: O(m(w)). (i) para cada nodo sucesor amarillo , , nuevo" ponero en el heap (ii) para cada nodo sucesor , , antiguo" corregir en caso necesario su distancia y su posiciòn en el heap. Su posiciòn se puede encontrar en el heapaddress. Dado que su distancia al nodo de origen disminuye (o no se correige) puede ser necesario elevarlo a la parte superior. Las posiciones en el heap de este nodo pueden modificarse en O(1). Costo para (i) y (ii): en total O(m(w) log n). Costo total para 2: O( log n • {Knoten w} m(w)) = O( e log n). Costo total para 1: O(min{n, e} log n), ya que un elemento se puede sacar del heap solo si antes se haia puesto. Costo total: O(e log n) (costo total de memoria: O(n+e)) 51

Prueba de correctitud: Aseveración: en todo momento se cumple para todo nodo verde: • Existe un camino mínimo de v 0 hasta u, que solo contiene nodos verdes. • Su longitud es dist(u). Prueba: por Induccion. Se debe mostrar esta aseveración para los nodos que pasan de amarillo a verde. De esta aseveración se desprende la correctitud del algoritmo. 52