Kapitel 6 Algorithmentheorie n Im vorangegangenen Kapitel wurde

Kapitel 6 Algorithmentheorie n Im vorangegangenen Kapitel wurde beschrieben, mit welchen Elementen Algorithmen aufgebaut werden, und was man dabei zu beachten hat. Dieses Kapitel geht nun darauf ein, ob ein Problem überhaupt algorithmisch fassbar ist, ob eine gefundener Algorithmus auch das tut was er soll und wieviel Zeit bzw. Platz er dafür benötigt. n Inhalt 1. Berechenbarkeit 2. Korrektheit 3. Komplexität Teile dieses Kapitels sind aus: R. Manthey: Vorlesung Informatik 1, Uni Bonn, 2001

6. 1 Berechenbarkeit n Wir haben den Begriff und die Elemente eines Algorithmus vorgestellt und Algorithmen zur Lösung von Problemen verwendet. In diesem Unterkapitel werden nun einige Fragen zur Anwendbar- und Sinnhaftigkeit von Algorithmen gestellt und beantwortet. n Inhalt: 1. 2. 3. 4. 5. 6. Einige Fragen Das Entscheidungsproblem Die Turing-Maschine Berechenbarkeit Rekursive Funktionen Church‘sche These H. Ernst: “Grundlagen und Konzepte der Informatik“, Vieweg-Verlag, 2000

6. 1. 1 Einige Fragen 1. Kann jedes Problem durch einen Algorithmus beschrieben werden, d. h. prinzipiell - bei genügender Sorgfalt - gelöst werden ? 2. Kann jeder Algorithmus in ein Programm übertragen werden ? n Welchen Anforderungen muss eine Programmiersprache genügen, damit jeder Algorithmus damit formuliert werden kann ? 3. Ist ein Computer grundsätzlich in der Lage, einen bekannten, als Programm formulierten Algorithmus auszuführen ? 4. Ist ein solcher Computer formalisierbar ? n n Wie sieht ein solches abstraktes Model aus ? Gibt es genau ein Model oder mehrere ? Sind diese Modelle äquivalent ? Gibt es andere Modelle oder Beschreibungsformen, diesem formalisierten Computermodell entsprechen ? n Frage 1 und Frage 4 sind wesentlich für den Begriff der Berechenbarkeit, Frage 2 wird im anschließenden Kapitel behandelt, Frage 4 ist Gegenstand der Vorlesung „Compilerbau“

6. 1. 2 Das Entscheidungsproblem n Bis weit ins 20 ste Jahrhundert war die Mehrzahl der Mathematiker (insb. David Hilbert: 1862 -1942) der Ansicht, dass man von jeder Aussage algorithmisch beweisen könne, ob sie wahr oder falsch sein. n Anders ausgedrückt: Es sei entscheidbar, ob ein Problem lösbar oder unlösbar ist. n Die Frage, ob dies entscheibar ist oder nicht ging als Entscheidungsproblem in die Geschichte der Mathematik (und Informatik) ein. n Kurt Gödel wies in seinem Unvollständigkeits-Theorem 1931 nach, dass alle widerspruchsfreien axiomatischen Formulierungen der Zahlentheorie unentscheidbare Aussagen enthalten. n damit wurde insb. belegt, dass streng algorithmisch arbeitende Computer prinzipiell nicht jedes Problem lösen können. n Auf fast schon philosophischer Ebene wurde damit auch belegt, dass Wahrheit eine andere Qualität als Beweisbarkeit besitzt. n nicht alle „wahren“ Aussagen können auch bewiesen werden.

6. 1. 3 Die Turing-Maschine: Definition n Als abstraktes Modell eines Computers beschrieb Alan Turing (19121954) 1963 - also noch vor der Erfindung des Digitalrechners - eine nach ihm benannte abstrakte Maschine n Formal kann eine Turing-Maschine wie folgt beschrieben werden: n Alphabet: A = {a 0, . . . , an}, der Zeichenvorrat der Turing-Maschine, wobei a 0 das Leerzeichen ("blank") darstellt (Oft: a 1=0, a 2=1) n Bandinschrift: B: Z A eine Zuordnung, die jeder Stelle des rechtsseitig unendlichen Bandes ein Zeichen zuordnet. Dabei wird festgesetzt, dass B(k) = a 0 für alle bis auf endlich viele. n Kopfposition: k Z n Zustände: eine endliche Menge von Maschinenzuständen. Q = {q 0, . . . , qm} Darunter sind q 0, der Anfangszustand und H Q , die Menge der Haltezustände, ausgezeichnet. l Statt Haltzustände wird oft auch eine Halteaktion angegeben) n Turing-Tabelle: eine Übergangsrelation: d : A Q {r, l, n}, das jedem (gelesenen) Zeichen in Abhängigkeit eines Zustandes ein neues Zeichen, einen Folgezustand und eine Aktion (r, l, n} zuordnet

6. 1. 3 Die Turing-Maschine: Programm n Die Aktion: n "aj" das Überschreiben des unter dem Kopf befindlichen Zeichens durch aj, n r: das Verschieben des Kopfes nach rechts n l: das Verschieben des Kopfes nach links. falls die Maschine das unter dem Kopf im Zustand gelesene Zeichen q a 1 a 2 a 3 a 4. . . a 6 ak so ist die Aktion der neue Zustand aj, r oder l q‘

6. 1. 3 Die Turing-Maschine: Beispiel n Das „Busy beaver“-Problem: Wieviele „ 1“-en kann ein terminierendes Touring-Programm auf einem leeren Band mit einer vorgegebenen Anzahl von Zuständen maximal erzeugen. n In dieser Notation wird statt eines Übergangs in den Haltezustand (z. B. q 5) die Aktion „halt“ ausgeführt. 11 Schritte, 6 Einsen 96 Schritte, 13 Einsen n Der Rekord für |Z|=5 liegt bei 4096 „ 1“en (J. Buntrock, H. Marxen, 1989) n Es wurde gezeigt, dass es möglich ist, mehr als 4098 „ 1“en zu generieren - allerdings nicht wie.

6. 1. 4 Definition: Berechenbarkeit n Ein Problem ist genau dann algorithmisch lösbar, wenn es durch eine Turing-Maschine darstellbar ist. n Eine Funktion f(x) heißt berechenbar, genau dann wenn es einen Algorithmus (eine Turing-Maschine) gibt, der bei gegebenem x das Ergebnis f(x) liefert n Ein Computer ist äquivalent zu einer universellen Turing-Maschine. n d. h. ein Computer ist äquivalent zu einer Turing-Maschine, die jede andere Turing-Maschine simulieren kann. n Zur Simulation einer beliebigen Turing-Maschine muss auf dem Eingabeband eine Beschreibung der zu simulierenden Maschine codiert werden und außerdem deren Eingabeband gespeichert sein. n Die Menge verschiedener universeller Turing-Maschinen ist abzählbar - denn das Band ist binär codiert, jede Kombination lässt sich auf eine natürliche Zahl abbilden. Die Menge aller Funktionen f(x) ist überabzählbar (z. B. Funktionen die auf eine reelle Zahl abbilden) Es gibt (unendlich viele) nicht berechenbare Funktionen

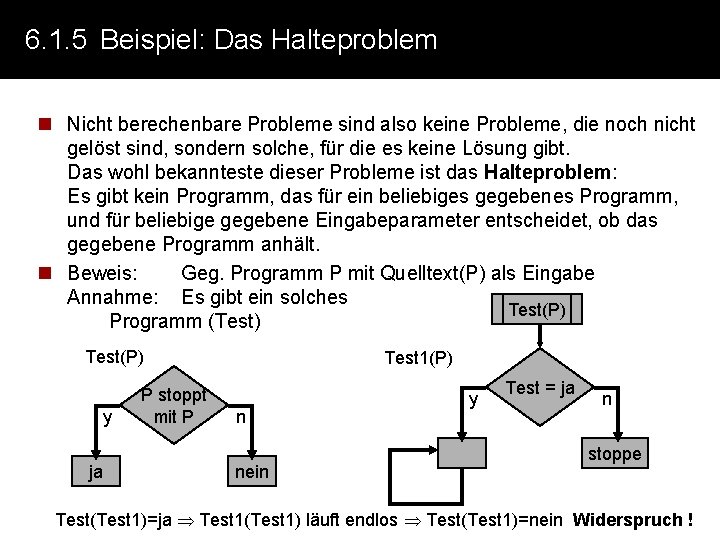
6. 1. 5 Beispiel: Das Halteproblem n Nicht berechenbare Probleme sind also keine Probleme, die noch nicht gelöst sind, sondern solche, für die es keine Lösung gibt. Das wohl bekannteste dieser Probleme ist das Halteproblem: Es gibt kein Programm, das für ein beliebiges gegebenes Programm, und für beliebige gegebene Eingabeparameter entscheidet, ob das gegebene Programm anhält. n Beweis: Geg. Programm P mit Quelltext(P) als Eingabe Annahme: Es gibt ein solches Test(P) Programm (Test) Test(P) y ja P stoppt mit P Test 1(P) n nein y Test = ja n stoppe Test(Test 1)=ja Test 1(Test 1) läuft endlos Test(Test 1)=nein Widerspruch !

6. 1. 6 Rekursive Funktionen n Es gibt innerhalb der mathematischen Funktionen zwei Unterklassen: n primitiv-rekursive Funktionen: l jede primitiv-rekursive Funktion ist berechenbar l es gibt berechenbare Funktionen, die nicht primitiv-rekursiv sind l primitiv-rekursive Funktionen lassen sich genau mit Algorithmen ohne Schleifenkonstrukte (aber mit Blockung) darstellen. n -rekursive Funktionen l jede -rekursive Funktion ist berechenbar l es gibt berechenbare Funktionen, die nicht -rekursiv sind l -rekursive Funktionen lassen sich mit Algorithmen mit Schleifenkonstrukte (und Blockung) darstellen. n Es gilt folgende Beziehung innerhalb von Funktionen: berechenbare Funktionen -rekursive Funktionen primitiv-rekursive Funktionen

6. 1. 6 Church‘sche These n Wir haben bislang verschiedene Äquivalenzen gefunden: n Primitiv und -rekursive Funktionen sind Teilmengen von berechenbaren Funktionen. n Eine Funktion ist genau dann berechenbar, wenn es eine Turing-Maschine zu deren Berechnung gibt, . n Die Darstellung mit Hilfe einer Turing-Maschine ist äquivalent mit der einer universellen Turingmaschinm, die wiederum eine Abstraktion eines Computers darstellt n Dies legt die Formulierung einer der Church‘schen These nahe: Alle im intuitiven Sinn vernünftigen Formalisierungen von Problemlösungen sind äquivalent n Wenn ein Problem nicht durch eine Turing-Maschine gelöst werden kann, so ist es algorithmisch überhaupt nicht lösbar n Da Begriffe wie „intuitiv“ und „vernünftig“ nicht definiert sind, ist die Church‘sche These nicht beweisbar.

6. 2 Korrektheit n Wir haben diskutiert, ob man jede (mathematische) Funktion berechnen kann und haben dabei die Äquivalenz eines Algorithmus‘ mit berechenbaren Funktionen gesehen. In diesem Unterkapitel geht es nicht mehr nur darum, ob eine Funktion berechenbar ist, bzw. ein Algorithmus für deren Berechnung existiert, sondern ob der gegebene Algorithmus tatsächlich das macht, was er machen soll n Inhalt 1. 2. 3. 4. 5. 6. 7. 8. U. Kastens: “Modellierung“, Vorlesung WS‘ 00/‘ 01, Uni Paderborn Ansatz Definition Logik zur Verifikation (C. A. R. Hoare) Regeln Terminierung Beispiele Beweis des Euklid‘schen Algorithmus Kritische Anmerkungen

6. 2. 1 Ansatz n Wir haben zu Beginn des Kapitels den Begriff der Korrektheit definiert: n partielle Korrektheit: Jedes berechnete Ergebnis genügt der Ausgabespezifikation, sofern die Eingaben der Eingabespezifikation genügt haben n Terminierung: Der Algorithmus hält nach endlich vielen Schritten mit einem Ergebnis an, sofern die Eingaben der Eingabespezifikation genügt haben n Zum Beweis der Korrektheit gehen wir also von der Eingabespezifikation aus und versuchen, mit den Aktionen (Statements) des Algorithmus die Ausgabespezifikation abzuleiten. n Die Eingabespezifikation wird dabei als Vorbedingung P(V) oder {P} und die Ausgabespezifikation Q(V) oder {Q} als Nachbedingung mathematisch formuliert n Über die Aktionen des Algorithmus wird die Vorbedingung über Zusicherungen Zi(V) zur Nachbedingung abgeleitet n Also: P(V) Z 1(V) . . . Zn(V) Q(V)

6. 2. 2 Definition: Korrektheit n Beispiel: Lösung der quadratischen Gleichung qugl (IN: p, q: real, OUT x 1, x 2: real) // Vorbedingung: (p*p)/4 > q // Nachbedingung: x 1 = (-b + sqr(p*p/4 -q)) / (2*a) // x 2 = (-b - sqr(p*p/4 -q)) / (2*a) { w : real; w = sqr(p*p/4 - q); x 1 = -p/2 + w; x 2 = -p/2 - w: } n Ein Algorithmus heißt korrekt bezüglich seiner Spezifikation, wenn für jeden Aufruf, der die Vorbedingung erfüllt, nach dem Aufruf des Algorithmus‘ die Nachbedingung erfüllt ist (und er terminiert) n Achtung: Die Vorbedingung ist vom Aufrufer zu erfüllen, die Nachbedingung ist durch den Algorithmus (bzw. den Implementierer) zu erfüllen.

6. 2. 3 C. A. R. Hoare: Logik zur Verifikation n C. A. R. Hoare formulierte 1969 ein Kalkül zum Beweis von Aussagen über Algorithmen und Programme n damit sind - im Gegensatz zum Testes - statische Aussagen über Zustände des Algorithmus ( Werte der Variablen) möglich. Diese Aussagen gelten für alle Ausführungen des Algorithmus n Durch logisch Schlüsse über die Elemente eines Algorithmus kann gezeigt werden, dass n an einer bestimmten Stelle im Algorithmus eine bestimmte Aussage gilt. n eine Aussage an jeder Stelle eines Teils des Algorithmus invariant gilt n Schleifen terminieren. Also: n ein Algorithmus aus jeder zulässigen Eingabe die geforderte Ausgabe berechnet

6. 2. 3 C. A. R. Hoare: Beispiel n min (IN: a, b: integer, OUT min: integer) // Vorbedingung: a, b > 0 (nicht unbedingt notwendig) // Nachbedingung: (min=a min=b) (min a) (min b) { if a<b then { // Z 1: a<b min = a; // Z 2: a<b min=a Z 3: min=a min b } else { // Z 4: b a min = b; // Z 5: b a min=b Z 6: min=b min a } // Z 7: (min=a min b) (min=b min a) // Z 8: (min=a min=b) (min a) (min b) = Q } n Damit ist aus der Vorbedingung P mit Hilfe der Anweisung in min() die Nachbedingung Q formal abgeleitet worden.

6. 2. 3 C. A. R. Hoare: Vorgehen n Aussagen über den Algorithmenzustand, über Werte von Variablen werden in den Algorithmus eingefügt: n { P } A 1 { Q } A 2 { R } n bedeutet: Q gilt immer zwischen der Ausführung von A 1 und der Ausführung von A 2 n Beispiel: { i + 1 0} i : = i + 1; { i 0 } a [i] : = k; {. . . } n Zur Verifikation eines Algorithmus muss für jede Anweisung S ein Nachweis geführt werden: n { Vorbedingung P } S { Nachbedingung Q } n nachweisen: Wenn vor der Ausführung des Schrittes S die P gilt, dann gilt Q nach der Ausführung von S, falls S terminiert. n Beispiel: { i + 1 0} i : = i + 1; {i 0} mit Zuweisungsregel nachweisen n Die Aussagen werden entsprechend der Struktur von S verknüpft. Für jede Anweisungsform wird eine spezielle Schlussregel angewandt. n Die Spezifikation liefert Vorbedingung und Nachbedingung des gesamten Algorithmus:

6. 2. 4 Regel: Zuweisung n Die Zuweisung x = expr wertet den Ausdruck expr aus und weist das Ergebnis der Variablen x zu. Es gilt dann: {P[x/expr]} x : = expr {P} oder {P(x)} x = f(x) {P(f--1(x))} n P[x/expr] steht für die Substitution von x durch expr in P n Die Nachbedingung P erhält man dadurch, dass man jedes Vorkommen von expr in der Vorbedingung durch x (die linke Seite der Zuweisung) ersetzt n Wenn man also zeigen will, dass nach der Zuweisung eine Aussage P für x gilt, muss man zeigen, dass vor der Zuweisung dieselbe Aussage P für expr gilt. n Beispiele: n {a>0} x = a {x>0} n {i+1>0} i=Succ(i) {i>0}: f(x)=Succ, f-1(x)=Pred(x), {P(Pred(x+1)}=(i+1 -1>0) n {i+1>0} i = i+1 {i>0}

6. 2. 4 Regel: Zuweisung - Beispiele n {P[x/expr]} x : = expr {P} 1. alle Aussagen der Vorbed. für expr, gelten für x in der Nachbedingung 2. Aussagen der Vorb. über x gelten in der Nachbedingung nicht mehr 3. Die Nachbedingung P erhält man dadurch, dass man jedes Vorkommen von expr in der Vorbedingung durch x ersetzt l ggf. ist die Vorbedingung so umzuformen, dass expr explizit Teil der Vorbedingung ist (auf der linken Seite einer Aussage) 1. 2. 3. 4. 5. 6. 7. {y=5} x=y {a>0 x>7} x=a {a>0 z>0} x=a {i+1>0} i=i+1 {i 0} {i+1>0} {i=2} {i+1=3} {z=5} x=1 {x=5} {x>0 x>7} {x>0 z>0} {i>0} i=i+1 {i=3} {z=5 x=1} falsch wg. Punkt 2 z>0 ist nicht betroffen passend umformen z nicht betroffen, x neu

6. 2. 4 Regel: Konsequenz n Abschwächung der Nachbedingung wenn gilt und dann gilt auch {P} S {R} {Q} {P} S {Q} Beispiel {a+b>0} S {x>0} {X 0} {a+b>0} S {X 0} n Verschärfung der Vorbedingung wenn gilt und dann gilt auch {P} {R] {R} S {Q} {P} S {Q} n Beispiel (Notation: Im Algorithmus können Implikationen in Ausführungsrichtung eingefügt werden) {a+b>0} x = a+b; {x>0} {2*x 0} y = 2 * x {y 0}

6. 2. 4 Regel: Sequenz n Folgendes Schema lässt sich auf eine Sequenz von Aktionen (Statements) anwenden: wenn gilt {P} S {R} und dann gilt auch {R} S 2 {Q} {P} S 1, S 2 {Q} n Beispiel: {x>0 y>0} a = x; {a>0 y>0} b = y; {a>0 b>0} {x>0 y>0} a = x; {a>0 y>0} {a>0 b>0} n Bei trivialen Ableitungen können die Zwischenschritte (Zusicherungen, Aussagen) auch weggelassen werden: {x>0 y>0} a = x; b = y; {a>0 b>0}

6. 2. 4 Regel: Bedingte Anweisung n Schema: wenn gilt und {P B} S {Q} dann gilt auch {P B} {Q} {P} if B then S {Q} n Um die Nachbedingung einer bedingten Anweisung zu beweisen, muss 1. aus der Vorbedingung und der Anweisungs-Bedingung über die Anweisung die Nachbedingung nachgewiesen werden 2. aus der Vorbedingung und der Negation der Anweisung die Nachbedingung direkt folgen n Beispiel: n Gegeben: if a<0 then a = -a n Beweise, dass der Algorithmus a 0 für alle a liefert: 1. {P a<0} {P -a>0} a=-a {P a>0} {P a 0} 2. {P (a<0)} {P a 0} dann gilt auch {P} if a<0 then a=-a {P a 0}

6. 2. 4 Regel: Bedingte Anweisung - Notation n Beispiel: n Gegeben: if a<0 then a = -a n Beweise, dass der Algorithmus a 0 für alle a liefert: 1. {P a<0} {P -a>0} a=-a {P a>0} {P a 0} 2. {P (a<0)} {P a 0} dann gilt auch {P} if a<0 then a=-a {P a 0} n Notation: {P} if a<0 then {P a<0} {P -a>0} a = -a {P a>0} {P a 0} // leere Alternative: {P (a<0)} {P a 0}

6. 2. 4 Regel: Einfache Alternative n Schema: wenn gilt und {P B} S 1 {Q} dann gilt auch {P B} Ss {Q} {P} if B then S 1 else S 2 {Q} n Aus der gemeinsamen Vorbedingung P muss für beide Alternativen dieselbe Nachbedingung Q nachweisbar sein n Beispiel: Gegeben: a>0, b>0, a b und ein Algorithmus (s. u) n Beweise, dass nach den Operationen immer noch gilt: a>o, b>0 {a>0 b>0 a b} if a>b then {a>0 b>0 a b a>b} {b>0 a-b>0} a = a-b; {b>0 a>0} else {a>0 b>0 a b} {a>0 b-a>0} b = b-a; {a>0 b>0}

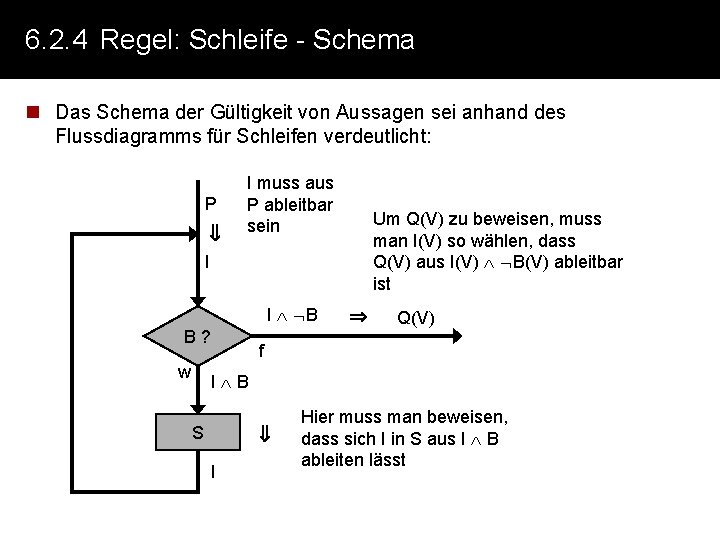
6. 2. 4 Regel: Schleife n Schema: wenn gilt dann gilt auch {P I B} S {P} {I} while B { S } {I B Q} Schleifeninvariante // I = n Schleifeninvarianten sind Zusicherungen in Schleifen, die beim Durchlaufen des Schleifenkörpers erhalten bleiben. Es gelte n n n P Q I B S Zusicherung über Variable vor Schleifeneintritt Zusicherung über Variable nach Schleifenende Schleifeninvariante Wiederholbedingung der Schleife Statements (Aktionen) im Schleifenkörper n Die Nachbedingung einer Schleife ist über die Invariante nachgewiesen nachzuweisen, wenn gilt: 1. P I die Invariante muss vor Schleifeneintritt wahr sein 2. (I B) I die Invariante darf in Schleife nicht verändert werden 3. (I B) Q die Nachbedingung muss sich nach Verlassen der Schleife aus der Invariante nachweisen lassen

6. 2. 4 Regel: Schleife - Schema n Das Schema der Gültigkeit von Aussagen sei anhand des Flussdiagramms für Schleifen verdeutlicht: P I muss aus P ableitbar sein Um Q(V) zu beweisen, muss man I(V) so wählen, dass Q(V) aus I(V) B(V) ableitbar ist I I B B? w Q(V) f I B S I Hier muss man beweisen, dass sich I in S aus I B ableiten lässt

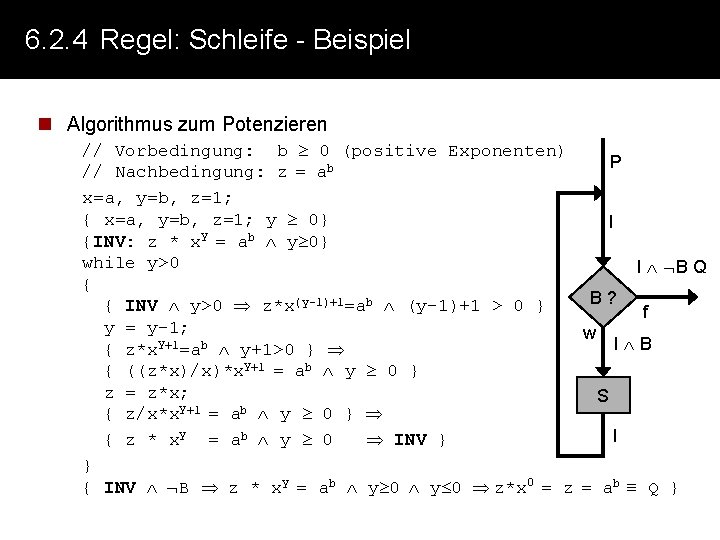
6. 2. 4 Regel: Schleife - Beispiel n Algorithmus zum Potenzieren // Vorbedingung: b 0 (positive Exponenten) P // Nachbedingung: z = ab x=a, y=b, z=1; { x=a, y=b, z=1; y 0} I y {INV: z * x = ab y 0} while y>0 I B Q { B? { INV y>0 z*x(y-1)+1=ab (y-1)+1 > 0 } f y = y-1; w y+1 b I B { z*x =a y+1>0 } { ((z*x)/x)*xy+1 = ab y 0 } z = z*x; S y+1 b { z/x*x = a y 0 } I { z * xy = ab y 0 INV } } { INV B z * xy = ab y 0 z*x 0 = z = ab Q }

6. 2. 4 Regel: Schleife - Schleifeninvariante n Das Finden der „richtigen“ Invariante kann ganz schön kniffelig sein: n Ein paar „Tips“: n Gegeben: Vorbedingung b 0 Zu beweisen: Nachbedingung z = ab n Wenn die Nachbedingung nicht gegeben ist, versuche die Semantik des Algorithmus‘ zu verstehen, z. B. anhand von Beispielen. n Betrachte die Anweisungen in der Schleife: Meist wird etwas vergrößert (z. B. die Variable der Abbruchbedingung), während etwas anderes verkleinert wird - oder umgekehrt. Kombiniere diese: z * xy n Setze Ein- und Ausgabevariablen in Bezug zueinander z * xy = a b n Beachte, dass aus INV und B(V) Q(V) ableitbar sein soll Das bedeutet, dass man die In variante aus der Nachbedingung konstruieren kann, indem man die negierte Bedingung mit berücksichtigt z * xy = ab y=0 z*x 0 = z = ab Q

6. 2. 5 Terminierung n Die Terminierung einer Schleife muss separat nachgewiesen werden n Beweis der Terminierung 1. Gib einen ganzzahligen Ausdruck E an über Variablen, die in der Schleife vorkommen und zeige, dass E bei jeder Iteration durch S verkleinert wird 2. Zeige, dass E nach unten begrenzt ist, z. B. dass 0 E eine Invariante der Schleife ist 3. Zeige, dass die Grenze auch erreicht wird. n E kann auch monoton vergrößert und nach oben begrenzt sein n Beweis der Nicht-Terminierung: Beweise, 1. dass R B eine Invarianz der Schleife ist (also R in die Schleife geht) und dass es eine Variablenbelegung gibt, so dass R B vor der Schleife gilt 2. dass R einen speziellen Zustand charakterisiert, in dem die Schleife nicht anhält n Es gibt Schleifen, für die man nicht entscheiden kann, ob sie für jede Vorbedingung terminieren.

6. 2. 5 Terminierung - Beispiele n { a>0 b>0 } while a b { while a>b { a=a-b } while a<b { b=b-a } } // terminiert n { a>0 b>0 } while a b { a=a-b } while a<b { b=b-a } } // terminiert nicht immer (a = 2*b) n { n n>1 } while n>1 if n gerade then n = n/2 else n=3*n+1 // Terminierung unbewiesen

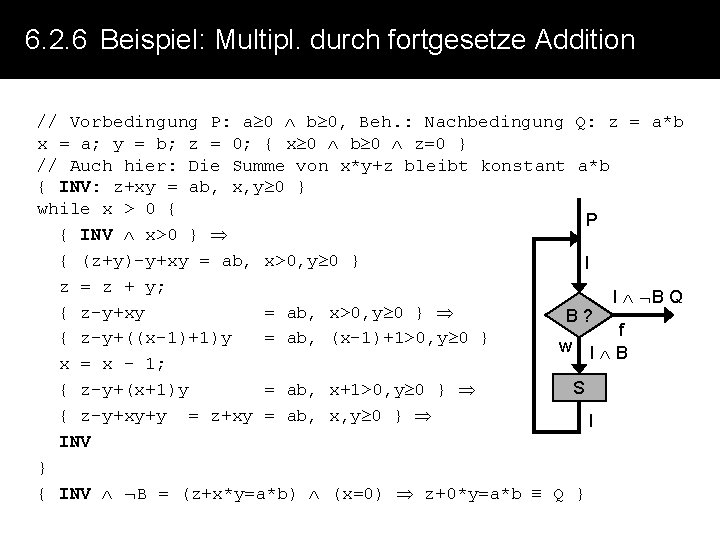
6. 2. 6 Beispiel: Multipl. durch fortgesetze Addition // Vorbedingung P: a 0 b 0, Beh. : Nachbedingung Q: z = a*b x = a; y = b; z = 0; { x 0 b 0 z=0 } // Auch hier: Die Summe von x*y+z bleibt konstant a*b { INV: z+xy = ab, x, y 0 } while x > 0 { P { INV x>0 } { (z+y)-y+xy = ab, x>0, y 0 } I z = z + y; I B Q { z-y+xy = ab, x>0, y 0 } B? f { z-y+((x-1)+1)y = ab, (x-1)+1>0, y 0 } w I B x = x - 1; S { z-y+(x+1)y = ab, x+1>0, y 0 } { z-y+xy+y INV = z+xy = ab, x, y 0 } } { INV B = (z+x*y=a*b) (x=0) z+0*y=a*b Q } I

6. 2. 6 Beispiel: Die ägyptische Bauernmultiplikation // Vorbedingung P: a 0 b 0, Beh. : Nachbedingung Q: z = a*b x = a; y = b; z = 0; { x, y 0 z=0 x=a y=b } // Schleife verdoppelt x und halbiert y: Invariante: INV = { z+x*y = a*b x, y 0 } while x > 0 { { INV x>0 } if (odd(x) then { (z+y)-y+x*y = a*b) x>0, y 0 } z = z+y; { odd(x) z-y+x*y = a*b x>0, y 0 } // leere Anweisung { even(x) z+x*y = a*b x>0, y 0 } { odd(x) z-(2 y/2)+x*(2 y/2) = a*b x>0, (2 y/2) 0 even(x) z+x*(2 y/2) = a*b x>0, (2 y/2) 0 } y = y * 2; { odd(x) z-y/2+x*y/2 = a*b x>0, y/2 0 even(x) z+x*y/2 = a*b x>0, y/2 0 } { odd(x) z-y/2+(2(x div 2)+1)*y/2 = a*b (2(x div 2)+1)>0, y 0 even(x) z+(2(x div 2))*y/2 = a*b 2(x div 2) >0, y 0 } x = x div 2; // div = Ganzzahldivision { odd(2 x+1) z-y/2+(2 x+1)*y/2 = a*b (2 x+1)>0, y/2 0 even(2 x) z+ 2 x *y/2 = a*b 2 x >0, y/2 0 } { z-(y - y(2 x+1))/2 = z-(y-2 xy-y)/2 = z-(-2 xy/2)= z+xy = a*b z + 2 x * (y*2) = z+xy = a*b } INV } { INV B = (z+x*y=a*b) (x=0) z+0*y=a*b Q }

6. 2. 6 Beispiel: Euklid‘scher Algorithmus (gg. T) // Vorbedingung P: a>0 b 0, Beh. : Nachbed. Q: x=gg. T(a, b) x = a; y = b; // Z 1: x>0 b 0 // Die Summe von x*y+z bleibt konstant a*b { INV: (gg. T(x, y) = gg. T(a, b)) (x>0 y 0) } while y > 0 { { INV (y>0) } r = x mod y; // r ist Rest aus x/y x = y; y = r; { gg. T(y, x mod y) = gg. T(x, y) = gg. T(a, b) } { INV } } // I(A) B(V) = (gg. T(x, y) = gg. T(a, b)) (y=0) // (gg. T(x, 0) = x = gg. T(a, b)) = Q(V)

6. 2. 7 Beweis Euklid‘scher Algorithmus I n Zu beweisen: gg. T(y, x mod y) = gg. T(x, y), x>0, y 0 Der Beweis stützt sich auf einen Hilfssatz, der zunächst bewiesen wird n Hilfssatz: Seien a 0, b. Dann gilt für alle d ( „|“: Ist Teiler von) a) d | a b) d | b d | (a mod b) d | a n Beweis: a) Es sei a mod b = r. Dann ist a - r durch b teilbar. Also ist a - r auch durch d teilbar. Da a durch d teilbar ist, muss auch r durch d teilbar sein, also gilt d | (a mod b). b) Wiederum sei a mod b = r. Dann ist a - r durch b und damit durch d teilbar. Da r durch d teilbar ist, muss auch a durch d teilbar sein, d. h. es gilt d | a.

6. 2. 7 Beweis Euklid‘scher Algorithmus II n Beweis: Es wird gezeigt, dass ggt(a, b) und ggt(b, a mod b) sich gegenseitig teilen und daher gleich sein müssen. 1. Sei d = ggt(a, b). Dann gilt d | a und d | b und nach dem Hilfssatz d | (a mod b) Nach Definition des ggt gilt d | b d | (a mod b) d | ggt(b, a mod b) 2. Sei nun umgekehrt d = ggt(b, a mod b). Dann gilt d | b und d | (a mod b) und nach dem Hilfssatz d | a Nach Definition des ggt gilt d | a d | b d | ggt(a, b) n Mit 1. d=ggt(a, b) | ggt(b, a mod b) und 2. d=ggt(b, a mod b) | ggt(a, b) ist gezeigt, dass ggt(a, b) = ggt(b, a mod b)

6. 2. 8 Kritische Anmerkungen n Die Verifikation entspricht einer mathematischen Beweisführung und kann entsprechend kniffelig, aufwändig, wenn nicht gar unmöglich sein. n Durch formale Überprüfung der Korrektheit, lassen sich Schlüsselstellen eines Algorithmus‘ (eines Programmes) verifizieren n Durch das Denken mit Zusicherungen, Invarianten und mathematische Folgerungen wird die Erstellung fehlerfreier Programme gefördert. n Auch wenn es semi-automatische Systeme zur formalen Verifikation von Algorithmen gibt, ist es praktisch nicht möglich, auch nur halbwegs komplexe Programmsysteme damit zu verifizieren n Selbst wenn es möglich wäre, Algorithmen vollständig formal zu beweisen, so wäre dies keine Garantie, dass ein Programmsystem entsprechend den Wünschen eines „Kunden“ funktioniert. Dazu gehören alle Mechanismen eines ordentlichen Software-Engineerings.

6. 3 Komplexität n In diesem Kapitel haben wir den Begriff „Berechenbarkeit“ definiert als all das, was algorithmisch beschreibbar ist. Wir haben eine Methode vorgestellt, mit der man (meist) zeigen kann, dass ein Algorithmus das tut was er soll. Was noch fehlt - und hier behandelt werden soll - ist die Frage nach dem Zeit- und Platzbedarf eines Algorithmus. n Inhalt 1. 2. 3. 4. 5. 6. Wie „gut“ ist ein Algorithmus Die O-Notation Häufige O-Ausdrücke Einige Regeln Quantitatives Platzbedarf

6. 3. 1 Qualität eines Algorithmus n Die Abarbeitung eines Algorithmus benötigt „Resourcen“, vor allem: n Zeit n Platz Laufzeit des Algorithmus Speicherplatzbedarf des Algorithmus n Problem bei der Resourcenermittlung - der Resourcenbedarf ist Abhängig von: n n n der Problemgröße (z. B. Multiplikation einer 10 x 10 bzw. 100 x 100 Matrix) der Eingabewerte (z. B. Sortieren einer bereits sortierten Menge) der Fragestellung (bester, mittlerer, schlechtester Fall) der Güte der Implementierung (z. B. (un)geschickte Typwahl) der Hard- und Software (z. B. Schneller Rechner, optimierter Compiler) n Es gibt auch Qualitätsmerkmale eines Algorithmus, der sich nicht am Resourcenbedarf festmachen (aber das ist eine andere Geschichte. . . ) n Wartbarkeit n Robustheit n „Eleganz“ . . .

6. 3. 2 Die O-Notation: Definition n Definition: Eine Funktion g(n) wird O(f(n)) genannt („Die Laufzeit, der Aufwand, die Zeitkomplexität von g(n) ist O(f(n))“), falls es Konstanten c und n 0 gibt, so dass: g(n) c f(n), für fast alle n > no ist n f(n) ist damit eine obere Schranke für die Laufzeit des Algorithmus (allerdings nur ab einem bestimmten c und n 0) n Beispiel: n Bei der Analyse eines Algorithmus hat sich herausgestellt, dass die Laufzeit g(n) = 3 n 2 + 7 n - 1 ist. n Behauptung: Die Laufzeit von g(n) ist O(n 2), also f(n)=n 2, n Beweis: Es muss Konstanten c und n 0 geben, so dass gilt 3 n 2+7 n-1 c n 2, für alle n > n 0 setze n 0=7 und c=4, dann gilt: 3 n 2+7 n-1 3 n 2+7 n 3 n 2+n 2 = 4 n 2

6. 3. 2 Die O-Notation: Schranken n Die Notation gibt nur eine obere Schranke der Komplexität , das muss nicht notwendigerweise die beste Schranke sein. n Beispiel: Eine weitere obere Schranke für g(n) = 3 n 2 + 7 n - 1 ist auch O(n 3), welche sicher nicht die beste ist. n Bei der Suche nach der Größenordnung von f(n) wird man versuchen, das kleinste f(n) zu finden, für das g(n) < c. f(n) Dieses ist dann eine kleinste, obere Schranke für den Aufwand n Zur Bestimmung des tatsächlichen asymptotischen Aufwands wird man also noch eine größte, untere Schranke h(n) = (g(n)) suchen für die gilt: limn h(n)/f(n) = 1 n Eine untere Schranke ist die Zeit, die jeder Algorithmus (ab einem n>n 0) benötigt n Das ist im Allgemeinen viel schwieriger !

6. 3. 2 Die O-Notation: Achtung n Achtung ! Die Konstanten c und n 0 werden üblicherweise nicht angegeben und können sehr groß sein n Beispiel: Algorithmus A habe eine Laufzeit von O(n 2) Algorithmus B für das gleiche Problem eine Laufzeit von O(1, 5 n) Welcher Algorithmus ist besser ? n schnelle Antwort: A (das stimmt auch für große n) n bessere Antwort: Wie groß ist n ? Wie groß sind die Konstanten ? n z. B. für c. A=1000 und c. B=0, 001 n c. An 2 c. B 1, 5 n Bis hier ist B besser als A 1 10 20 50 103 105 4 105 2, 5 106 107 1, 5 10 -3 1, 8 10 -2 3, 3 6, 4 105 4, 1 1014

6. 3. 3 Häufige O-Ausdrücke: O(1) n Teile von Ausdrücken, die eventuell ein „paar“ Mal durchlaufen werden, wobei die (maximale) Anzahl der Durchläufe nicht abhängig von den Eingabewerten sind, haben konstante Laufzeit: O(1) n Beispiel: max, i, y : integer; max = 0; y << Tastatur; if (y < 20) then max=10 else max=100; for i=1 to max { y = y+1; } n Die Anzahl der Schleifendurchläufe ist zwar abhängig von y (entweder 20 oder 100), die maximale Anzahl aber nicht (immer 100, egal wie groß oder klein y ist)

6. 3. 3 Häufige O-Ausdrücke: O(log n) - rekursiv n Rekursive Algorithmen, die in jedem Schritt die Menge der Eingabedaten halbieren haben eine Laufzeit von O(log n) n eigentlich O(ld n), aber da ld n 3, 322 log b = c log b ist O(ld b)=O(log n) n Beispiel: Suche in einem sortierten Binärbaum search (IN: x: integer; tree: *node; OUT: found: boolean) { if tree == nil then { // there is no tree to search => x not found = false; return; // ATTENTION: return already here } if (x < node. value) then search(x, node. left, found) else if (x > node. value) then search(x, node. right, found) else if (n == node. value) found=true; } n Zeitbedarf: Tn = Tn/2+1 (Tn = Zeitbedarf für n, n 2, T 1=0) Annahme (o. B. d. A. ): n = 2 k, T 2 k = T 2 k-1 +1 = T 2 k-2 +1+1 =. . . = T 20 + k = k Tn= k = ldn

6. 3. 3 Häufige O-Ausdrücke: O(n) - rekursiv n Rekursive Algorithmen, die in jedem Schritt die Menge der Eingabedaten halbieren aber dazu jedes Element betrachten müssen haben eine Laufzeit von O(n) n Beispiel: Suche in einer sortierter Liste (array) mit 0 am Ende search (IN: x: integer; list: *liste; OUT: found: boolean) { i : integer; if (list[1]==0) then found = false; // list with no element i=1; while (list[i] <> 0) i=i+1 // get length of list if (x==list[i/2]) then found = true; else if (x<list[i/2]) then { list[i/2+1]=0; search(x, &list[1], found} }; else search(x, &list[i/2+1], found); } n Zeitbedarf: Tn = Tn/2+ n (Tn = Zeitbedarf für n, n 2, T 1=0) Annahme (o. B. d. A. ): n = 2 k, T 2 k = T 2 k-1 + n = T 2 k-2 + n/2+n =. . . = T 20 +n/2+n/4 +. . . + 0 = 2 n-2 O(n)

6. 3. 3 Häufige O-Ausdrücke: O(n) - iterativ n Iterative Algorithmen die eine lineare Liste durchlaufen deren Länge abhängig von der Menge der Eingabeelemente ist (einfache Schleife), haben die Laufzeit O(n) n Beispiel: Suche in einer sortierter Liste (array) mit 0 am Ende search (IN: x: integer; list: *liste; OUT: found: boolean) { i : integer; found = false; // initialize OUT-value i=1; while ((list[i] <> 0) and (not found)) { i=i+1; if (list[i]==x) then found = true; } } n Anmerkung: n Dieser Algorithmus funktioniert auch mit unsortierten Listen n Warum dann einen rekursiven, teilenden Algorithmus ? l Anzahl „eingeschränkter“ Vergleiche O(n) l Anzahl „vollständiger“ Vergleiche O(log n)

6. 3. 3 Häufige O-Ausdrücke: O(n) - rekursiv n Rekursive Algorithmen, die Eingabedaten in zwei Hälften aufspalten, und beide Hälften getrennt abarbeiten, haben eine Laufzeit von O(n) n Beispiel: Erstellen eines „Lineals“ (siehe auch: Skript Dr. Geisse) linael (IN: links, rechts, höhe: integer) { mitte : integer; if (höhe>0) then { mitte = (links + rechts) / 2; zeichne (mitte, höhe); lineal (links, mitte, höhe-1); lineal (mitte, rechts, höhe-1); } } n Zeitbedarf: Tn = 2 Tn/2+ 1 (Tn = Zeitbedarf für n, n 2, T 1=0) Annahme (o. B. d. A. ): n = 2 k, T 2 k = 2 T 2 k-1 + 1 1/2 T 2 k = T 2 k-1 + 1/2 = 2 T 2 k-2 + 1/2 1/4 T 2 k = T 2 k-2 + 1/4 . . . 1/2 k T 2 k = T 20 + 1/2 + 1/4 +. . . + 1/2 k = 1 - 1/2 k T 2 k = 2 k-1 Tn = n-1 Laufzeit O(n)

6. 3. 3 Häufige O-Ausdrücke: O(n log n) n Rekursive Algorithmen, die Eingabedaten in zwei Hälften aufspalten, und die Eingabedaten einmal durchlaufen (davor, währenddessen, oder danach), haben eine Laufzeit von O(n log n) n Beispiel: Sortieren einer Liste a : array[1. . max] of integer (C. A. R. Hoare) Quicksort (IN: l, r: integer) { // l left, r right index i, j, x : integer; // i, j: indexes, x, y: elemets i=l; j=r; // initialize i with left, j with right index x = a[(l+r)/2}] // get element in the middle do { // walk with i from left, with j from right while a[i]<x { i=i+1 } // skip smaller elements from left while a[j]>o { j=j-1 } // skip larger elements from right if (i<=j) then { exchange(a[i], a[j]); i=i+1; j=j 11 } } while i<=j // i is now right of j -> stop loop if l<j then sort(l, j); // sort left part (only if exists) if i<r then sort(i, r); // sort right part (only if exists) n Zeitbedarf: Tn = 2 Tn/2+ n (Tn = Zeitbedarf für n, n 2, T 1=0) Annahme (o. B. d. A. ): n = 2 k, (d. h. k = ld n) T 2 k = 2 T 2 k-1 + 2 k 1/2 k T 2 k = T 2 k-1/2 k-1 + 1 = T 2 k-2/2 k-2 + 1 =. . . =k 1/2 k T k = k T k = 2 k k T = n log n Laufzeit O(n log

6. 3. 3 Häufige O-Ausdrücke: O(n 2) - rekursiv n Rekursive Algorithmen, die Eingabedaten jeweils um eins verringern, dabei aber alle Daten betrachten müssen, haben eine Laufzeit von O(n 2) n Beispiel: Sortieren einer Liste a : array[1. . max] of integer Straight. Selection (IN: l, r: integer) { // l left, r right index i: integer; // index i = l; // start with left element while (i<r) { // walk through complete list // if an element is smaller, bring it to the left if (a[i]<a[l]) then exchange(a[i], a[l]); i = i+1; } if (l<r) then Straight. Selection (l+1, r); } n Zeitbedarf: Tn = Tn-1+ n (Tn = Zeitbedarf für n, n 2, T 1=1) Tn = Tn-1 + n = Tn-2 + n-1 + 1 = Tn-3 + n-1 + n-2 + 1 =. . . = 1+2+3+. . +n Tn = (n(n+1))/2 = 1/2 n 2 + 1/2 n Laufzeit O(n)

6. 3. 3 Häufige O-Ausdrücke: O(n 2), O(n 3) - iterativ n Iterative Algorithmen die eine Liste - deren Länge abhängig von der Menge der Eingabeelemente ist - (fast) sooft durchlaufen, wie die Liste lang ist (doppelt verschachtelte Schleife), haben die Laufzeit O(n 2) n Beispiel: Sortieren einer Liste a : array[1. . max] of integer Straight. Selection (IN: l, r: integer) { // l left, r right index i: integer; // index i = l; // start with left element for i=1 to r-1 // walk through complete list { for j=i+1 to r // walk through rest of list { if (a[j]<a[i]) then exchange(a[i], a[j]); } } } n Dreifach verschachtelte Schleifen haben eine Laufzeit von O(n 3) n Beispiel: Multiplikation zweier Matrizen

6. 3. 4 Einige Regeln n Hat ein Algorithmus eine Laufzeit, die mit einem Polynom k-ten Grades darstellbar ist (aknk + ak-1 nk-1 +. . . + a 0) , so ist die Laufzeit O(nk) n Beispiel: Laufzeit: 9 n 3 + 7 n - 1000 Laufzeit O(n 3) n Wird ein Teil A mit Laufzeit O(x) vor einem Teil B mit Laufzeit O(y) ausgeführt, so ist die Gesamtlaufzeit das Maximum der Laufzeiten. n Beispiel: Laufzeit A ist O(n 2), Laufzeit B ist O(n) Laufzeit A, B = O(n 2) + O(n) = O(n 2) n Wird ein Teil A mit Laufzeit O(x) innerhalb eines Teiles B mit Laufzeit O(y) ausgeführt, so ist die Gesamtlaufzeit das Produkt der Laufzeiten. n Beispiel: Laufzeit A ist O(n 2), Laufzeit B ist O(n) Laufzeit A(B) = Laufzeit B(A) = O(n 2) O(n) = O(n 3) n Beispiel: Eine Dreifach verschachtelte Schleife (O(n 3)) ist eine Schleife O(n) in einer zweifach verschachtelten Schleife (O(n 2)) : O(n 3) = O(n 2) O(n)

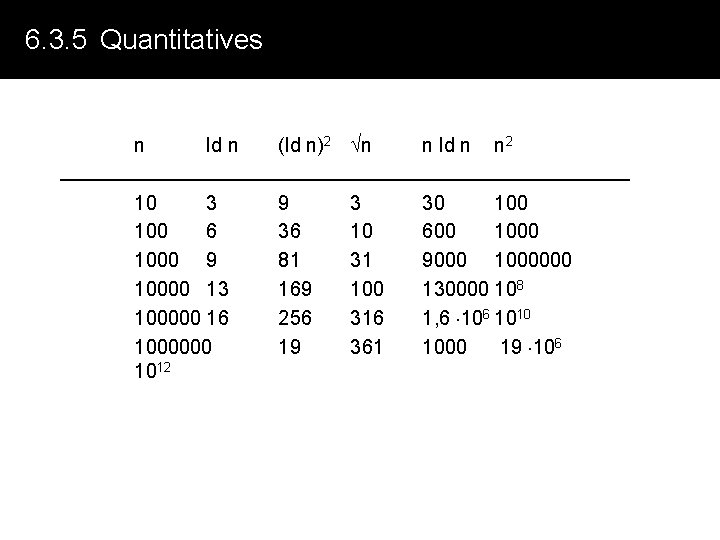
6. 3. 5 Quantitatives n ld n 10 3 100 6 1000 9 10000 13 100000 16 1000000 1012 (ld n)2 n n ld n 9 36 81 169 256 19 30 100 600 1000 9000 1000000 130000 108 1, 6 1010 1000 19 106 3 10 31 100 316 361 n 2

6. 3. 6 Platzbedarf n Unter „Aufwand“ wird i. A. der zeitliche Aufwand, also die Zeitkomplexität verstanden n Manchmal ist auch die Platzkomplexität bzw. Speicherbedarf relevant. Darunter versteht man dann, ganz entsprechend zur Zeitkomplexität, eine obere Schranke für den Speicherbedarf eines Algorithmus für ein Problem mit einer Eingabemenge der Größe n. n Auch beim Speicherbedarf von Algorithmen existieren die „Komplexitätsklassen“ (n, n 2, n log n, . . . ) n Auch beim Speicherbedarf unterscheiden sich „geschickte“ und „ungeschickte“ Algorithmen für die Lösung eines gegebenen Problems. n Da Computerspeicher endlich, die Zeit aber potentiell unendlich ist hat der Speicherbedarf oft die höhere Priorität. n Meist wird daher der Algorithmus gewählt, der sehr Nahe am minimal möglichen Speicherbedarf bei möglichst optimalem Aufwand liegt.

6. 3. 6 Platzbedarf n Oft kann man eine bessere Zeitkomplexität zu Lasten des Speicherbedarfs erreichen (und umgekehrt) n Beispiel: Trivialer Hashsort (Unsortierte Liste a: array [1. . n] of type) b: array [1. . max(type)] // max(type) is largest element in type, // e. g. max(unsigned integer) = 65535 i, j : integer; for i=1 to n { b[a[i]] = a[i]; } j = 1; for i=1 to max(type) { // shift to beginning of list if ((not_empty(b[i])) and (i<>j)) then { b[j]=b[i]; j=j+1; } } n 1. Schleife + 2. Schleife: O(n) + O(1) = O(n) n Man wägt daher Speicherbedarf und Zeitkomplexität gegeneinander ab.

6. 4 Zusammenfassung des Kapitels n Berechenbarkeit: 1. Einige Fragen und das Entscheidungsproblem 2. Die Turing-Maschine und der Begriff der Berechenbarkeit 3. Rekursive Funktionen und die Church‘sche These n Korrektheit 1. 2. 3. 4. Ansatz und Definition Logik zur Verifikation: Die Hoare‘schen Regeln Beispiele und Beweis des Euklid‘schen Algorithmus Kritische Anmerkungen n Komplexität 1. 2. 3. 4. Wie „gut“ ist ein Algorithmus und die O-Notation Häufige O-Ausdrücke und einige Regeln bei deren Anwendung Quantitatives Platzbedarf