Kapitel 4 Taktische Planungsprobleme Konfiguration und Dimensionierung c

Kapitel 4 Taktische Planungsprobleme (Konfiguration und Dimensionierung) (c) Prof. Richard F. Hartl Operations Management

Zusammenhang der verschiedenen Ebenen strategische Grundsatzentscheidungen Konkretisierung und Umsetzung in der taktischen Planung durch Konfigurierungs und Dimensionierungs entscheidungen Bestmögliche Nutzung der konfigurierten Produktionsanlagen in der operativen Ebene (c) Prof. Richard F. Hartl Operations Management 2

4. 1 Konfiguration von Werkstattfertigungs Produktionssystemen starke Unterscheidung der zu bearbeitenden Aufträge (z. B. in der Teileproduktion im Maschinenbau): n Keine Anordnung der Arbeitssysteme nach dem Objektprinzip möglich, da kein einheitlicher Materialfluss existiert n Anordnung nach dem Funktionsprinzip: Hier werden Arbeitssysteme, die gleichartige Funktionen (Operationen, Arbeitsgänge) durchführen können, räumlich in einer Werkstatt (Stanzerei, Dreherei, Galvanik) zusammengefasst. (c) Prof. Richard F. Hartl Operations Management 3

Werkstattproduktion n n n Aufträge müssen regelmäßig auf ihre Bearbeitung an einer Maschine oder auf den Transport zur nächsten Maschine warten Wartevorgänge führen zu (unerwünschten) Zwischenlagerbeständen von angearbeiteten Erzeugnissen Leerzeiten, wenn eine Maschine auf einen Auftrag wartet, weil dessen voriger Arbeitsgang in einer anderen Werkstatt noch nicht abgeschlossen ist oder weil er auf ein Transportmittel wartet. Gänzliche Verhinderung dieser unerwünschten Effekte nicht möglich Milderung der Effekte durch intelligente Einlastungsstrategien (operativ) und sinnvolle Anordnung der Werkstätten (taktisch) Typisches Konfigurationsproblem: (quadratisches) Zuordnungsproblem (c) Prof. Richard F. Hartl Operations Management 4

4. 1. 1 (lineares) Zuordnungsproblem (linear assignment problem, LAP) Das einfachste Optimierungsproblem der innerbetrieblichen Standortplanung ist das (lineare) Zuordnungsproblem. Gegeben: n Maschinen (Aktivitäten, Arbeiter) n mögliche Standorte (Zeitpunkte, Projekte) cij. . . Kosten des Betriebs von Maschine i an Standort j Jede Maschine ist an einem Standort zu betreiben, wobei an keinem Standort mehr als eine Maschine betrieben werden darf. Die Gesamtkosten sind zu minimieren. (c) Prof. Richard F. Hartl Operations Management 5

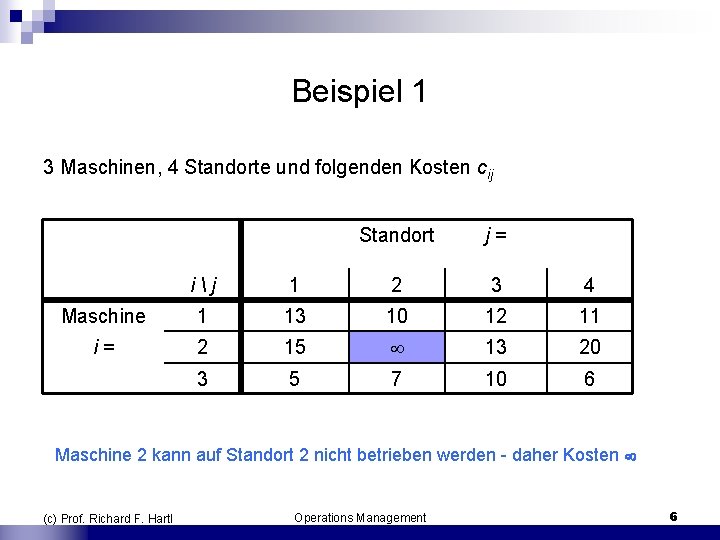
Beispiel 1 3 Maschinen, 4 Standorte und folgenden Kosten cij Standort j = i j 1 2 3 4 Maschine 1 13 10 12 11 i = 2 15 13 20 3 5 7 10 6 Maschine 2 kann auf Standort 2 nicht betrieben werden daher Kosten (c) Prof. Richard F. Hartl Operations Management 6

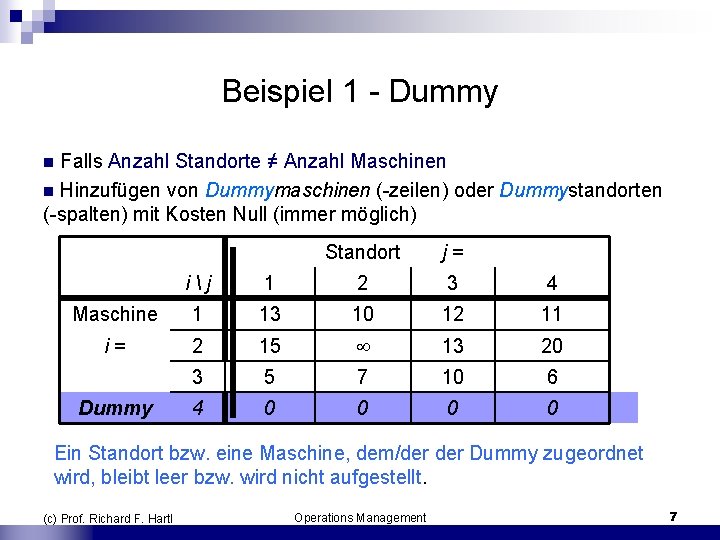
Beispiel 1 Dummy n Falls Anzahl Standorte ≠ Anzahl Maschinen n Hinzufügen von Dummymaschinen ( zeilen) oder Dummystandorten ( spalten) mit Kosten Null (immer möglich) Standort j = i j 1 2 3 4 Maschine 1 13 10 12 11 i = 2 15 13 20 3 5 7 10 6 4 0 0 Dummy Ein Standort bzw. eine Maschine, dem/der Dummy zugeordnet wird, bleibt leer bzw. wird nicht aufgestellt. (c) Prof. Richard F. Hartl Operations Management 7

LP Formulierung 1 wenn Maschine i auf Standort j betrieben wird, xij = 0 sonst Kosten: Nebenbedingungen: = 1 für i = 1, . . . , n. . . jede Maschine 1 zuordnen = 1 für j = 1, . . . , n. . . genau 1 Masch. pro Standort = 0 oder 1 für i = 1, . . . , n und j = 1, . . . , n (c) Prof. Richard F. Hartl Operations Management 8

4. 1. 1. 1 Formulierung als Transportproblem n Vergleich der LP Formulierungen von TP und LAP n Jedes LAP kann als Spezialfall eines Transportproblems angesehen werden, wobei jede Maschine als Anbieter mit "Kapazität" 1 und jeder Standort als Abnehmer mit „Nachfrage" 1 interpretiert wird. n Obwohl das Transportproblem grundsätzlich auch nicht ganzzahlige xij zulässt, ist sichergestellt, dass die optimale Lösung die Eigenschaft besitzt, dass genau n Variablen den Wert 1 besitzen und alle anderen Null sind. Damit erhält man eine zulässige Zuordnung. (c) Prof. Richard F. Hartl Operations Management 9

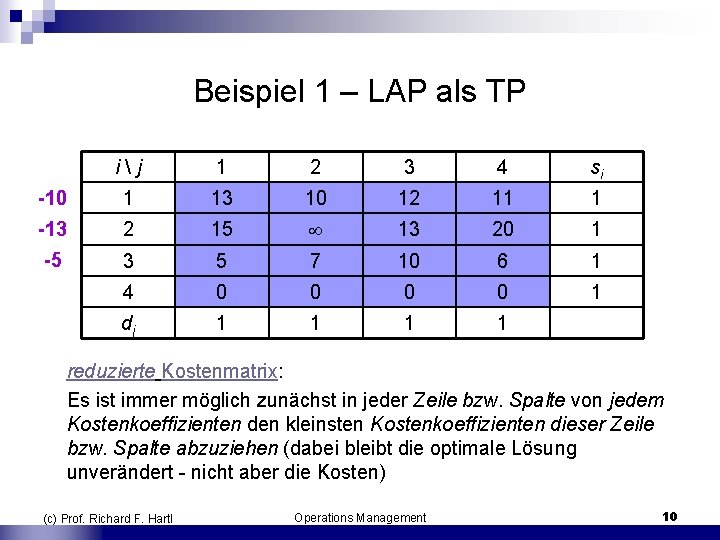
Beispiel 1 – LAP als TP i j 1 2 3 4 si -10 1 13 10 12 11 1 -13 2 15 13 20 1 -5 3 5 7 10 6 1 4 0 0 1 dj 1 1 reduzierte Kostenmatrix: Es ist immer möglich zunächst in jeder Zeile bzw. Spalte von jedem Kostenkoeffizienten den kleinsten Kostenkoeffizienten dieser Zeile bzw. Spalte abzuziehen (dabei bleibt die optimale Lösung unverändert nicht aber die Kosten) (c) Prof. Richard F. Hartl Operations Management 10

Reduzierte Kostenmatrix i j 1 2 3 4 1 3 0 2 2 2 0 3 0 2 1 7 5 1 Dummy 4 0 0 Spaltenminimummethode liefert hier optimale Lösung (reduzierten) Kosten = Null Die Maschinen 1, 2 und 3 werden auf Standort 2, 3 und 1 betrieben; Standort 4 bleibt frei (da ihm die Dummy Maschine 4 zugeordnet wurde). Bei größeren Problemen muss man zumeist noch einige Schritte des MODI verfahrens anschließen, um zur optimalen Lösung zu gelangen. (c) Prof. Richard F. Hartl Operations Management 11

4. 1. 1. 2 Ungarische Methode n Kuhn´s algorithm exaktes Verfahren n besteht aus mehreren Schritten: n ¨ ¨ ¨ Schritt I: Erzeugung von Nullen (Reduktion der Kosten) Schritt II: Suche nach einer optimalen Lösung Schritt III: Bestimmung einer minimalen Anordnung von Zeilen und Spalten, die alle Nullen enthält Schritt IV: Generierung zusätzlicher Nullen – Kostenreduktion Schritt V: Abbruch oder Wiederholung des Iterationsschrittes (c) Prof. Richard F. Hartl Operations Management 12

4. 1. 1. 2. 1 Schritt I Erzeugung von Nullen (Reduktion der Kosten) n Von jedem Element einer Spalte wird das kleinste Element dieser Spalte abgezogen; n Von jedem Element einer Zeile wird das kleinste Element dieser Zeile abgezogen; n Wenn schon ein Element 0 ist, kann nichts abgezogen werden! n Man erhält so eine Matrix, die in jeder Zeile und in jeder Spalte mindestens eine Null aufweist. (c) Prof. Richard F. Hartl Operations Management 13

Beispiel 2 17, 5 15 9 5, 5 12 13 7 0, 5 6, 5 11, 5 8, 5 2 0 5 7, 5 6 6 0 16 16, 5 10, 5 12 15, 5 14, 5 11 5, 5 4, 5 8 14 17, 5 13 0 0 5, 5 12, 5 7, 5 13 9, 5 8, 5 12 17, 5 8, 5 1, 5 0 7 12 4, 5 8 8, 5 5 5, 5 12, 5 6, 5 0 0 6 11, 5 8, 5 2 0 5 7, 5 6 6 0 0 0 5, 5 12, 5 7, 5 8, 5 1, 5 0 7 12 K = 4, 5 + 8, 5 + 5, 5 + 0, 5 = 32 (c) Prof. Richard F. Hartl Operations Management 0, 5 14

Schritt II Suche nach einer optimalen Lösung n Man sucht eine Lösung, für die Kostensumme den Wert Null annimmt, wo also genau eine Null in jeder Zeile und jeder Spalte auftritt (umrahmte bzw. schattierte Nullen, s. u. ). n Falls das zutrifft, haben wir eine optimale Lösung gefunden. (c) Prof. Richard F. Hartl Operations Management 15

Beispiel 1 – nach Reduktion n 3 0 2 1 2 0 7 0 2 5 1 0 0 Optimale Lösung gefunden! Suche eine Zeile oder Spalte mit möglichst wenig Nullen (möglichst genau eine Null) und umrahme (schattiere) eine Null dieser Zeile oder Spalte! – hier ist vorläufig eine Zuordnung erfolgt. Durchkreuze alle Nullen in dieser Zeile oder Spalte (sodass in jeder Zeile oder Spalte mit einer umrahmten Null alle anderen Nullen durchkreuzt sind). In dieser Zeile bzw. Spalte kann ja keine Zuordnung mehr erfolgen. Danach sucht man wieder eine Zeile oder Spalte mit möglichst wenig nicht markierten Nullen, usw. , bis keine Null mehr umrahmt werden kann. (c) Prof. Richard F. Hartl Operations Management 16

Beispiel 2 – nach Reduktion 12, 5 6, 5 0 0 6 2. Null 11, 5 8, 5 2 0 5 1. Null 7, 5 6 6 0 3. Null 0 0 5, 5 12, 5 7, 5 4. Null 8, 5 1, 5 0 7 12 (c) Prof. Richard F. Hartl Noch keine optimale Lösung gefunden! (bzw. Optimalität nicht bewiesen) Operations Management 17

4. 1. 1. 2. 3 Schritt III n Bestimmung einer minimalen Anordnung von Zeilen und Spalten, die alle Nullen enthält a) Kennzeichne (z. B. durch ein Kreuz X) alle Zeilen, die keine umrahmten Nullen enthalten. b) Kennzeichne alle Spalten, die mindestens eine durchgekreuzte Null auf einer gekennzeichneten Zeile enthalten. c) Kennzeichne alle Zeilen, die eine umrahmte Null in einer gekennzeichneten Spalte enthalten. d) Wiederhole b) und c) bis keine Spalte oder Zeile mehr gekennzeichnet werden kann. e) Markiere mit einer durchgehenden Linie jede nicht gekennzeichnete Zeile und jede gekennzeichnete Spalte. (schattiert). Alle (umrahmten und durchgekreuzten) Nullen sind dann mit mindestens einer Linie markiert. (c) Prof. Richard F. Hartl Operations Management 18

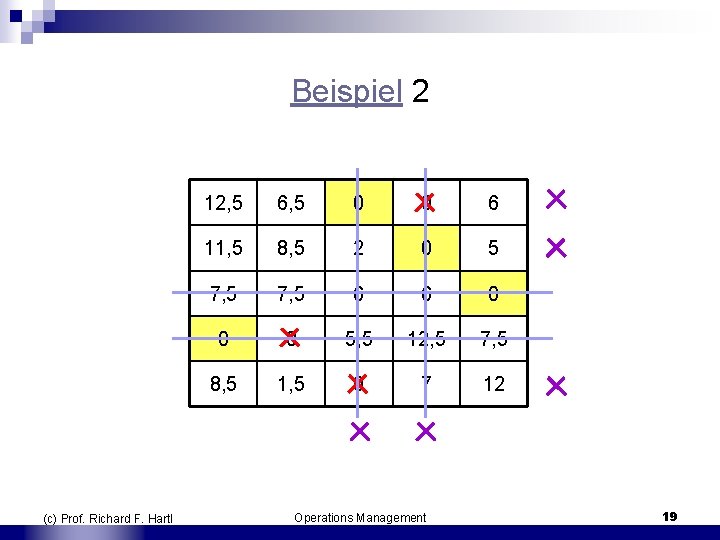
Beispiel 2 (c) Prof. Richard F. Hartl 12, 5 6, 5 0 0 6 11, 5 8, 5 2 0 5 7, 5 6 6 0 0 0 5, 5 12, 5 7, 5 8, 5 1, 5 0 7 12 Operations Management 19

Schritt IV Generierung zusätzlicher Nullen Kostenreduktion n Wähle unter allen nicht überdeckten Elementen das kleinste. n Dieses Element a wird von allen nicht überdeckten Elementen subtrahiert und zu allen doppelt überdeckten Elementen addiert n Es ist sichergestellt, dass durch diese Transformation die optimale Lösung nicht verändert wird n Allerdings werden die Gesamtkosten um a reduziert (Erhöhung der Reduktionskonstante) (c) Prof. Richard F. Hartl Operations Management 20

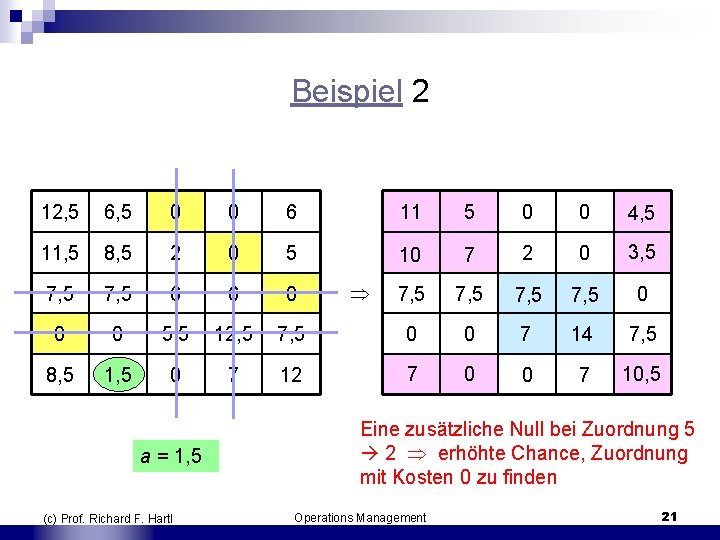
Beispiel 2 12, 5 6, 5 0 0 6 11 5 0 0 4, 5 11, 5 8, 5 2 0 5 10 7 2 0 3, 5 7, 5 6 6 0 7, 5 0 0 0 5, 5 12, 5 7, 5 0 0 7 14 7, 5 8, 5 1, 5 0 7 12 7 0 0 7 10, 5 a = 1, 5 (c) Prof. Richard F. Hartl Eine zusätzliche Null bei Zuordnung 5 2 erhöhte Chance, Zuordnung mit Kosten 0 zu finden Operations Management 21

Schritt V Abbruch oder Wiederholung des Iterationsschrittes n Wie in Schritt II wird versucht, eine optimale Zuordnung zu finden. n Gelingt dies nicht, müssen wir die Iteration ab Schritt II wiederholen. (c) Prof. Richard F. Hartl Operations Management 22

Beispiel 2 – Iteration 2 11 5 0 0 4, 5 Maschine 1 auf Standort 3 10 7 2 0 3, 5 Maschine 2 auf Standort 4 7, 5 0 Maschine 3 auf Standort 5 0 0 7 14 7, 5 Maschine 4 auf Standort 1 7 0 0 7 10, 5 Maschine 5 auf Standort 2 Optimale Zuordnung gefunden! Gesamtkosten: Addition aller Reduktionskonstanten aus Schritten I und IX: K= (4, 5 + 8, 5 + 5, 5 + 0, 5) + (1, 5) =33, 5 (c) Prof. Richard F. Hartl Operations Management 23

4. 1. 1. 3 Übungsbeispiele – Beispiel 1 Löse das folgende Zuordnungsproblem: 1 2 3 4 5 1 12 8 7 15 4 2 7 9 17 14 10 3 9 6 12 6 7 4 7 6 14 6 10 5 9 6 12 10 6 (c) Prof. Richard F. Hartl Operations Management 24

Beispiel 2 Sechs Ingenieuren sollen auf 6 Strandorte aufgeteilt werden. Die folgende Tabelle gibt den Nutzen für die Firma bei den entsprechenden Zuordnungen an: A B C D E F I 1 4 8 16 20 12 0 I 2 16 20 8 0 4 12 I 3 0 12 4 16 20 8 I 4 4 0 16 12 20 8 I 5 12 16 0 8 20 I 6 20 16 12 0 4 A: Morlaix B: Bayonne C: Strasbourg D: Annecy 4 E: Aix en Provence 8 F: Dunkerque Maximiere den Gesamtnutzen! [Hinweis: Transformation z. B. „Kosten“ = 20 Nutzen] (c) Prof. Richard F. Hartl Operations Management 25

Beispiel 3 Schwimm Mannschaft für 200 m Lagen Staffel; einer muss zuschauen. Die bisherigen Saisonergebnisse bzw. daraus prognostizieren Zeiten sind: Schwimmer Bewerb Carl Chris David Tony Ken Rücken 37, 7 32, 9 33, 8 37 35, 4 Brust 43, 4 33, 1 42, 2 34, 7 41, 8 Butterfly 33, 3 28, 5 38, 9 30, 4 33, 6 Freistil 29, 2 26, 4 29, 6 28, 5 31, 1 Es soll die optimale Zusammenstellung der Staffel ermittelt werden! (c) Prof. Richard F. Hartl Operations Management 26

4. 1. 2 Layoutplanung – quadratisches Zuordnungsproblem (QAP) n quadratische Zuordnungsproblem (QZOP, quadratic assignment problem, QAP): ist das typische mathematische Modell zur Beschreibung innerbetrieblicher Standortprobleme n vgl. dazu Kapitel 6 von Domschke, W. ; Drexl, A. : Logistik: Standorte (Bd. 3), 3. Aufl. , Oldenbourg, München, 1990: (c) Prof. Richard F. Hartl Operations Management 27

4. 1. 2. 1 Formulierung Zur Beschreibung benötigen wir die Distanzen zwischen den Standorten, und den Materialfluss zwischen den Organisationseinheiten: n n n Organisationseinheiten (OE) alle OE sind gleich groß paarweise vertauschbar n Standorte, jeder kann jede OE aufnehmen (genau eine) thi. . . Transportintensität, Stärke des Materialflusses von OE h nach OE i djk. . . Distanz zwischen Standort j und Standort k Entfernungen nicht notwendigerweise symmetrisch Transportkosten proportional zur transportierten Menge und zurückgelegten Entfernung (c) Prof. Richard F. Hartl Operations Management 28

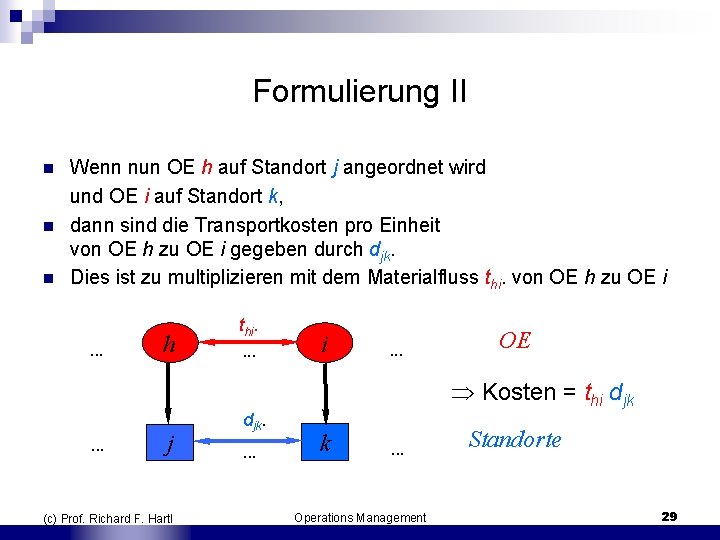
Formulierung II n n n Wenn nun OE h auf Standort j angeordnet wird und OE i auf Standort k, dann sind die Transportkosten pro Einheit von OE h zu OE i gegeben durch djk. Dies ist zu multiplizieren mit dem Materialfluss thi. von OE h zu OE i . . . h thi. . i . . . OE Kosten = thi djk . . . j (c) Prof. Richard F. Hartl djk. . k . . . Operations Management Standorte 29

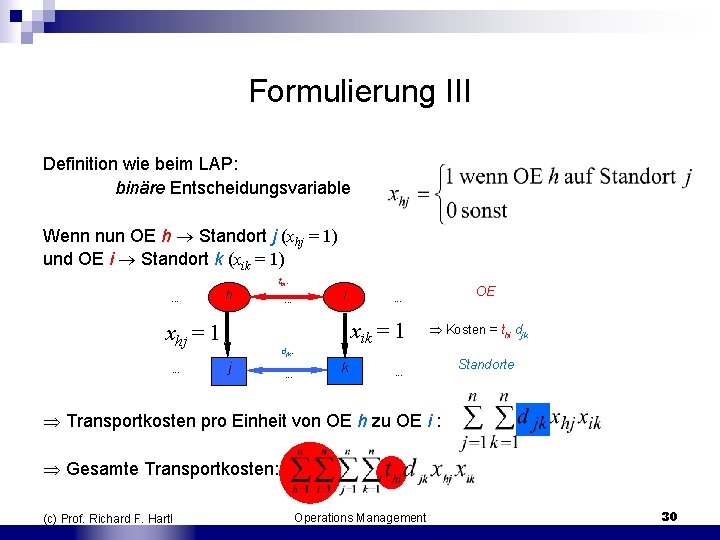
Formulierung III Definition wie beim LAP: binäre Entscheidungsvariable Wenn nun OE h Standort j (xhj = 1) und OE i Standort k (xik = 1). . . h thi. xhj = 1. . . i xik = 1 djk. j . . . k OE . . . Kosten = thi djk . . . Standorte Transportkosten pro Einheit von OE h zu OE i : Gesamte Transportkosten: (c) Prof. Richard F. Hartl Operations Management 30

Zielfunktion und Nebenbedingungen ZF: Minimiere die gesamten Transportkosten zwischen allen OE Quadratische Zielfunktion QAP Nebenbedingungen für h = 1, . . . , n . . . jede OE h an genau einem Standort j für j = 1, . . . , n . . . jeder Standort j bekommt genau eine OE h = 0 oder 1 (c) Prof. Richard F. Hartl ident mit dem LAP!!! . . . binäre Entscheidungsvariable Operations Management 31

Beispiel Ermittlung der Kosten bei 3 OE (1 , 2 , 3) und 3 Standorten (A, B, C) Distanzen zwischen den Standorten djk Transport intensitäten thi A B C mögliche Lösung: 1 A, 2 B, 3 C, also x 1 A = 1, x 2 B = 1, x 3 C = 1, alle anderen xij = 0 Die Nebenbedingungen sind erfüllt. Gesamten Transportkosten: 0*0 + 1*1 + 2*1 + 1*2 + 0*0 + 1*2 + 3*3 + 1*1 + 0*0 = 17 (c) Prof. Richard F. Hartl Operations Management 32

Beispiel Diese Lösung ist nicht optimal, da gerade die OE 1 und 3, zwischen denen ein starker Materialfluss herrscht, auf die entferntesten Standorte A und C gelegt wurden. Besser wäre z. B. : 1 C, 2 A und 3 B, also x 1 C = 1, x 2 A = 1, x 3 B = 1. mit den gesamten Transportkosten: 0*0 + 3*1 + 1*1 + 2*2 + 0*0 + 2*1 + 1*3 + 1*1 + 0*0 = 14 Distanzen Transportintensitäten 2 A 3 B 1 C (c) Prof. Richard F. Hartl Operations Management 33

Beispiel (Fortsetzung) dazu wurde die Matrix so umsortiert, dass die Zeilen und Spalten in der Reihenfolge 1 C, 2 A und 3 B, also C, A, B auftreten: (dabei sollte man die Umsortierung in 2 Schritten machen, zuerst Zeilen, dann Spalten, oder umgekehrt) (c) Prof. Richard F. Hartl Operations Management 34

4. 1. 2. 2 Eröffnungsverfahren: n Entstehung durch Kombination von jeweils einer der folgenden Möglichkeiten zur Wahl einer OE und zur Wahl eines Standortes. n Die schon angeordneten OE bilden so genannten Kern n In jeder Iteration wird eine weitere OE angeordnet, wobei folgende Prioritätsregeln zur Auswahl stehen (c) Prof. Richard F. Hartl Operations Management 35

1) Wahl einer (noch nicht angeordneten) OE A 1 A 2 A 3 A 4 jene, die zu sämtlichen (anderen) OE die größte Summe der Transportintensitäten besitzt a) jene, die zur zuletzt angeordneten OE die größte Transportintensität besitzt b) jene, die größte Transportintensität zu einer angeordneten OE besitzt jene, die zu allen angeordneten OE (Kern) die größte Summe der Transportintensitäten besitzt zufällige Auswahl der OE (c) Prof. Richard F. Hartl Operations Management 36

2) Wahl eines (noch nicht besetzten) Standortes B 1 B 2 B 3 B 4 jener, der die geringste Summe der Entfernungen zu sämtlichen Standorten besitzt einer, der dem zuletzt belegten Standorten benachbart ist a) einer, sodass die Summe der Transportkosten zum Kern minimal ist b) wie a) wobei noch versucht wird, den Platz mit benachbarten OE zu vertauschen c) ein Platz (frei oder besetzt) sodass die Summe der Transportkosten innerhalb des neuen Kernes minimal wird zufällige Auswahl des Standortes (c) Prof. Richard F. Hartl Operations Management 37

Beispiel Kombination der einfachsten Regeln A 1 und B 1: n OE nach fallender Summe der Transportintensitäten sortieren n Standorte nach steigender Summe der Entfernungen zu sämtlichen Standorten sortieren A B C D E F G H I n Manhatten Distanz zwischen den Standorten. (da symmetrisch, muss nur die obere Dreiecksmatrix betrachtet werden) (c) Prof. Richard F. Hartl Operations Management 38

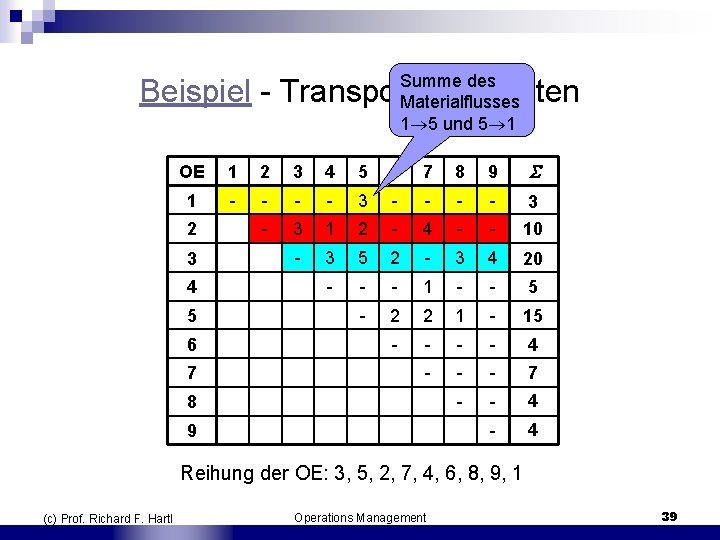
Summe des Materialflusses 1 5 und 5 1 Beispiel Transportintensitäten OE 1 2 3 4 5 6 7 8 9 1 3 2 3 1 2 4 10 3 3 5 2 3 4 20 4 1 5 5 2 2 1 15 6 4 7 7 8 4 9 4 Reihung der OE: 3, 5, 2, 7, 4, 6, 8, 9, 1 (c) Prof. Richard F. Hartl Operations Management 39

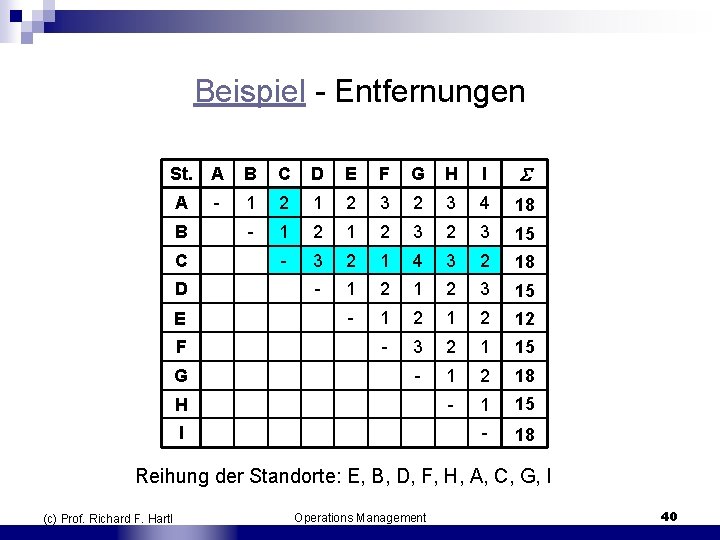
Beispiel Entfernungen St. A B C D E F G H I A 1 2 3 2 3 4 18 B 1 2 3 2 3 15 C 3 2 1 4 3 2 18 D 1 2 3 15 E 1 2 12 F 3 2 1 15 G 1 2 18 H 1 15 I 18 Reihung der Standorte: E, B, D, F, H, A, C, G, I (c) Prof. Richard F. Hartl Operations Management 40

Zuordnung n Reihung der OE: 3, 5, 2, 7, 4, 6, 8, 9, 1 n Reihung der Standorte: E, B, D, F, H, A, C, G, I n Zuordnung: OE 1 2 3 4 5 6 7 8 9 St. I D E H B A F C G (c) Prof. Richard F. Hartl Operations Management 41

Ermittlung der Kosten OE 1 2 3 4 5 6 7 8 9 1 3*3 2 2*2 4*2 3 3*1 5*1 2*2 3*2 4 1*2 5 2*1 2*2 1*1 6 7 8 9 3*1 1*2 (c) Prof. Richard F. Hartl Operations Management Auf 1 und 5 stehen I und B mit Transportintensität 3 3 (Distanz 1 5) * 3 (Intensität I B) Gesamtkosten = 61 42

4. 1. 2. 3 Verbesserungsverfahren n n Vertauschungen von OE Paaren vornehmen (wie eingangs im Beispiel) Man probiert, ob sich die Kosten verringern wenn 2 OE die Standorte tauschen. Wenn es die Rechenzeit erlaubt, kann man auch versuchen, OE Tripeln zu vertauschen Bei paarweisen Vertauschungen gibt es verschiedene Möglichkeiten: (c) Prof. Richard F. Hartl Operations Management 43

paarweise Vertauschungen Auswahl der Paare, deren Vertauschung überprüft wird: C 1 alle n(n 1)/2 Paare C 2 eine bestimmte Teilmenge aller Paare C 3 zufällige Auswahl n Auswahl der Paare, die vertauscht werden: D 1 jenes gemäß C überprüfte Paar, bei dem sich die größte Kostensenkung ergibt (bestes Paar) D 2 das erste gemäß C überprüfte Paar, bei dem sich eine Kostensenkung ergibt (erstes Paar) n (c) Prof. Richard F. Hartl Operations Management 44

Qualität der Lösungen I n Kombination C 1 mit D 1: Rechenaufwand höher als bei den anderen Varianten ¨ Lösungsgüte besser als bei den anderen Varianten Oft wird zu Beginn C 2 gewählt und später C 1. (Kombination C 1 und D 2 wäre 2 opt beim TSP. ) ¨ n CRAFT : sehr bekanntes (heuristisches) Lösungsverfahren ¨ entspricht Kombination C 1 und D 1 (für OE mit gleichem Platzbedarf) ¨ (c) Prof. Richard F. Hartl Operations Management 45

Qualität der Lösungen II n zufällige Auswahl (C 3 und D 2): recht gute Resultate ¨ beste Vertauschung aus der Menge der überprüften Lösungen ergibt manchmal eine Verschlechterung jedoch kein Nachteil (Gefahr des Hängenbleibens in lokalen Optima verringert sich) „Metaheuristiken“ in Modul Transportmanagement ¨ n Literatur: sämtliche Kombination der Grundideen bzw. Varianten unter A, B, C und D (c) Prof. Richard F. Hartl Operations Management 46

4. 1. 2. 4 Umlaufmethode n Heuristik n Kombination der Ideen von Eröffnungs und Verbesserungsverfahren Bestandteilen: n Initialisierung (i = 1): Ordne die OE mit der größten Summe der Transportintensitäten [A 1] in der Mitte des Standortträgers an (d. h. wo die Summe der Distanzen zu allen anderen Standorten minimal ist [B 1]). ¨ Iteration i (i = 2, . . . , n): ordne die i te OE zu ¨ (c) Prof. Richard F. Hartl Operations Management 47

Teil 1 Auswahl einer OE und eines freien Platzes: n wähle jene OE, die zu allen im Kern angeordneten OE die größte Summe der Transportintensitäten besitzt [A 3] n ordne sie auf einen freien Standort zu, so dass die Summe der Transportkosten zum Kern (bzw. innerhalb des neuen Kernes) minimal ist [B 3 a] (c) Prof. Richard F. Hartl Operations Management 48

Teil 2 Verbesserungsschritt ab Iteration i = 4: n versuche paarweise Vertauschungen der eben angeordneten OE mit allen anderen im Kern angeordneten OE [C 2] n wenn eine Verbesserung gefunden ist, führe diese Änderung durch und beginne wieder mit Teil 2 [D 2] Das Verfahren endet mit Abschluss von Iteration i = n, nachdem alle OE angeordnet sind. (c) Prof. Richard F. Hartl Operations Management 49

Beispiel – Teil 1 Initialisierung (i = 1): E = Zentrum Dort wird zunächst OE 3 angeordnet. A D G (c) Prof. Richard F. Hartl B E 3 H Operations Management C F I 50

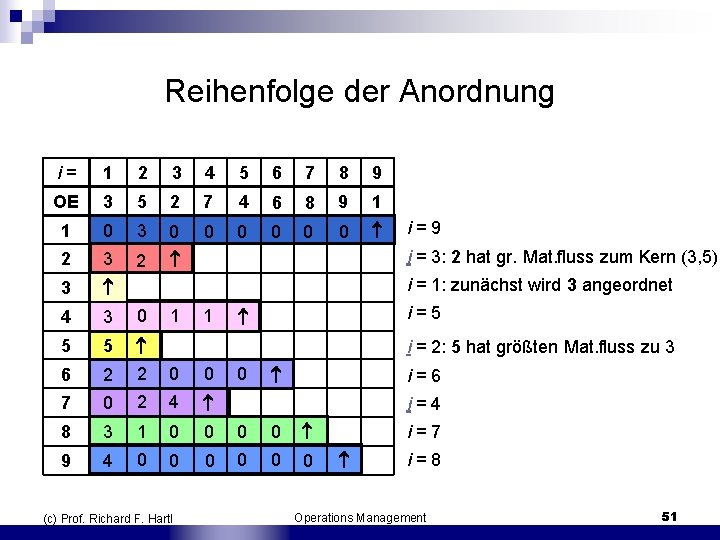
Reihenfolge der Anordnung i = 1 2 3 4 5 6 7 8 9 OE 3 5 2 7 4 6 8 9 1 1 0 3 0 0 0 i = 9 3 i = 3: 2 hat gr. Mat. fluss zum Kern (3, 5) 3 2 0 0 2 0 i = 1: zunächst wird 3 angeordnet 4 3 0 1 1 i = 5 5 5 i = 2: 5 hat größten Mat. fluss zu 3 6 2 2 0 0 0 i = 6 7 0 2 4 i = 4 8 3 1 0 0 i = 7 9 4 0 0 0 i = 8 (c) Prof. Richard F. Hartl Operations Management 51

Beispiel – Teil 1 Iteration i = 2 unter allen OE ist der Materialfluss von 5 zum Kern 3 maximal n Distanzen d. BE = d. DE = d. FE = d. HE = 1 gleichzeitig minimal D gewählt, n D 5 E 3 In Schritt i = 2 wird also D 5 zugeordnet. (c) Prof. Richard F. Hartl A B C Operations Management F G H I 52

Beispiel – Teil 1 Iteration i = 3 unter allen OE ist der Materialfluß von 2 zum Kern (3, 5) maximal n Suche Standort X, sodass d. XE t 23 + d. XD d 25 = d. XE 3 + d. XD 2 minimal wird: (A, B, G od. H) X = A d. AE 3 + d. AD 2 = 2 3 + 1 2 = 8 X = B d. BE 3 + d. BD 2 = 1 3 + 2 2 = 7 X = F d. FE 3 + d. FD 2 = 1 3 + 2 2 = 7 X = G d. GE 3 + d. GD 2 = 2 3 + 1 2 = 8 A B 2 C X = H d. HE 3 + d. HD 2 = 1 3 + 2 2 = 7 n B, F oder H B gewählt In Schritt i = 3 wird also B 2 zugeordnet. n (c) Prof. Richard F. Hartl Operations Management D 5 E 3 F G H I 53

Beispiel – Teil 1 Iteration i = 4 unter allen OE ist der Materialfluss von 7 zum Kern (2, 3, 5) maximal n Suche Standort X, sodass d. XE t 73 + d. XD t 75 + d. XB t 72 = d. XE 0 + d. XD 2 + d. XB 4 minimal wird n aus Lageplan nur A kommt in Frage In Schritt i = 4 wird also zunächst A 7 zugeordnet. n (c) Prof. Richard F. Hartl Operations Management 54

Beispiel – Teil 2 Versuche A mit E, B bzw. D zu vertauschen und ermittle jeweils die Kosten der Zuordnung: Aus Teil 1: E 3, D 5, B 2, A-7 = 18 probiere E 3, D 5, A 2, B 7 1 5+2 3+1 0+1 2+2 2+1 4 = 21 probiere E 3, A 5, B 2, D 7 2 5+1 3+1 0+1 2+2 4 = 25 probiere A 3, D 5, B 2, E 7 1 5+1 3+2 0+2 2+1 4 = 18 n Kosten =1 5+1 3+2 0+2 2+1 4 Kosten = Vertauschung A mit E wäre möglich ohne Kostenänderung. Da aber keine Verbesserung möglich ist: lasse Lösung wie aus Teil 1. u. s. w. (c) Prof. Richard F. Hartl Operations Management 55

Beispiel – Teil 2 n Nach 8 Iterationen ohne Teil 2: Kosten = 54 n Mit Teil 2 (letzte OE 9 mit 4 vertauscht): Kosten = 51 n Händisches durchrechnen ist für größere Probleme offensichtlich sehr mühsam n am Computer sind die Iterationen einfach zu implementieren. (c) Prof. Richard F. Hartl Operations Management 56

4. 1. 2. 5 Verfahren bei ungleichen Platzbedarf der OE n Anordnung der OE meist in einem Raster aus kleinen Quadraten weist jeder OE die nötige Anzahl benachbarter kleiner Quadrate zu n Eröffnungs und Verbesserungsverfahren auch hier anwendbar bei Vertauschungen kann sich die Gestalt der OEs ändern ¨ bei ungleicher Größe sind Verschiebungen nötig ¨ (c) Prof. Richard F. Hartl Operations Management 57

Beispiel n n Die Vertauschung von 3 und 5 ist unproblematisch Bei Vertauschung von 1 und 3 müssen die OE 2 oder 4 die Gestalt verändern. 1 4 2 5 3 (c) Prof. Richard F. Hartl Operations Management 58

4. 2 Konfiguration von Produktionsinseln Inselproduktion: n liegt zwischen Fließfertigung (Massenfertigung) und Werkstattfertigung (Einzelfertigung) n Arbeitssysteme unterschiedlicher Funktion werden räumlich zusammengefasst n jeder Produktionsinsel wird eine Erzeugnisfamilie (mit ähnlichen benötigten Ressourcen) zugeordnet n Voraussetzung ¨ Erzeugnisfamilien müssen sich auf natürliche Weise bilden lassen (c) Prof. Richard F. Hartl Operations Management 59

Vorteile n kurze Transportwege (zumeist innerhalb einer Insel) n geringe Umrüstzeiten wegen hoher Fertigungsverwandtschaft in Erzeugnisfamilie n hohe Flexibilität (bzgl. kurzfristigen Änderungen der Produktionsaufgaben) n geringer Investitionsbedarf (mit konventioneller Technologie realisierbar) n Übersichtlichkeit einfache Produktionssteuerung n Motivation und Zufriedenheit der Mitarbeiter durch Identifikation mit "ihren" Produkten n niedrige Losgrößen möglich, kurze Durchlaufzeiten (c) Prof. Richard F. Hartl Operations Management 60

4. 2. 1 Binäre Sortierung n Einfache Methode eine Gruppierung vorzunehmen n Matrixdarstellung: Bearbeitung des jeweiligen Erzeugnis auf der jeweiligen Maschinen n Auffassung diese Einträge zeilen und spalten weise als Binärzahlen n Sortierung der Zeilen in absteigender und der Spalten in aufsteigender Reihenfolge (c) Prof. Richard F. Hartl Operations Management 61

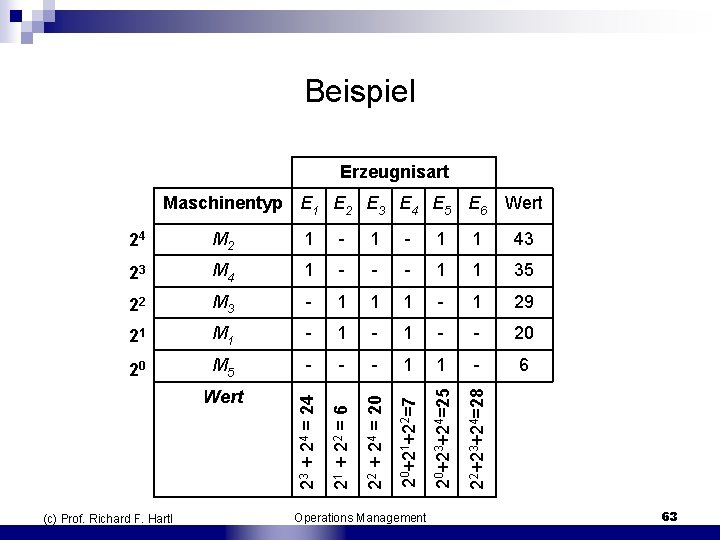
Beispiel n n Gegeben: 5 Maschinen; 6 Erzeugnisse, die jeweils auf eine Auswahl der Maschinen zu bearbeiten sind Maschinen/Erzeugnis Matrix: Maschinentyp Erzeugnisart Wert E 1 E 2 E 3 E 4 E 5 E 6 M 1 1 1 M 2 1 1 22 + 24 = 20 20 + 21 + 2 3 + 25 = 43 M 3 1 1 20 + 22 + 2 3 + 24 = 29 M 4 1 1 1 20 + 21 + 2 5 = 35 M 5 1 1 21 + 22 = 6 25 (c) Prof. Richard F. Hartl 24 23 22 21 20 Operations Management 62

Beispiel Erzeugnisart 1 1 43 23 M 4 1 1 1 35 22 M 3 1 1 29 21 M 1 1 1 20 20 M 5 1 1 6 Wert 22 + 24 = 20 20+21+22=7 (c) Prof. Richard F. Hartl Operations Management 22+23+24=28 M 2 20+23+24=25 24 21 + 22 = 6 Wert 23 + 24 = 24 Maschinentyp E 1 E 2 E 3 E 4 E 5 E 6 63

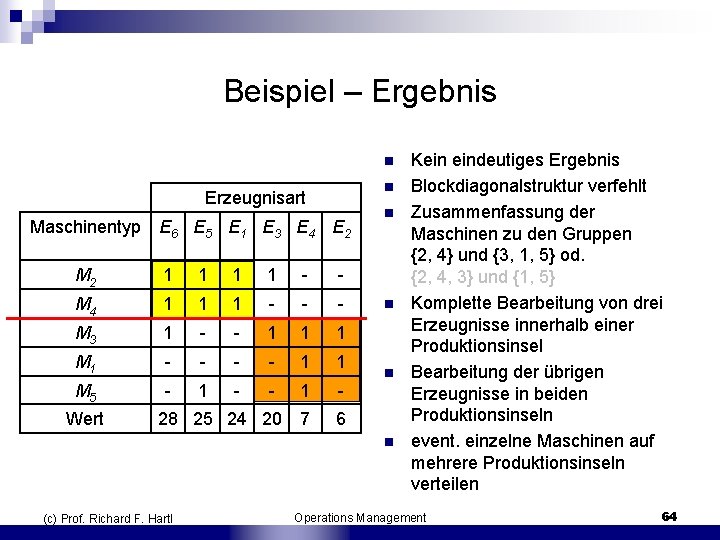
Beispiel – Ergebnis n n Erzeugnisart Maschinentyp E 6 E 5 E 1 E 3 E 4 E 2 M 2 1 1 M 4 1 1 1 M 3 1 1 1 1 M 1 1 1 M 5 1 1 7 6 Wert 28 25 24 20 n n (c) Prof. Richard F. Hartl Kein eindeutiges Ergebnis Blockdiagonalstruktur verfehlt Zusammenfassung der Maschinen zu den Gruppen {2, 4} und {3, 1, 5} od. {2, 4, 3} und {1, 5} Komplette Bearbeitung von drei Erzeugnisse innerhalb einer Produktionsinsel Bearbeitung der übrigen Erzeugnisse in beiden Produktionsinseln event. einzelne Maschinen auf mehrere Produktionsinseln verteilen Operations Management 64

4. 2. 2 Verfahren von Askin und Standridge Erweiterung der Gruppenbildung mittels der binären Sortierung. n jedes Erzeugnis wird innerhalb einer Maschinengruppe komplett bearbeitet n die Kapazitätsgrenzen der einzelnen Maschinen werden beachtet n jede Maschinengruppe nimmt nur eine vorgegebene Anzahl von Maschinen eines Typs auf n die maximale Anzahl von Maschinen innerhalb einer Gruppe ist vorgegeben (c) Prof. Richard F. Hartl Operations Management 65

Beispiel Verfahren von Askin und Standridge Beispiel: n n In einem Produktionssegment werden sieben Erzeugnisse auf insgesamt sechs Maschinentypen bearbeitet. Die Arbeitspläne zeigen auf welchen Maschinen ein Erzeugnis bearbeitet werden muss und welche Rüst bzw. Stückbearbeitungszeiten jeweils anfallen. Aufgrund des durchschnittlichen Periodenbedarfs kann somit ermittelt werden, welcher Anteil der Periodenkapazität einer Maschine jeweils für die Bearbeitung eines Erzeugnisses benötigt wird. Eine Gruppe besteht aus höchstens 4 Maschinen 9/4 = 2, 25 mindestens 3 Inseln Es darf höchstens je eine Maschine eines bestimmten Typs in einer Gruppe enthalten sein (c) Prof. Richard F. Hartl Operations Management 66

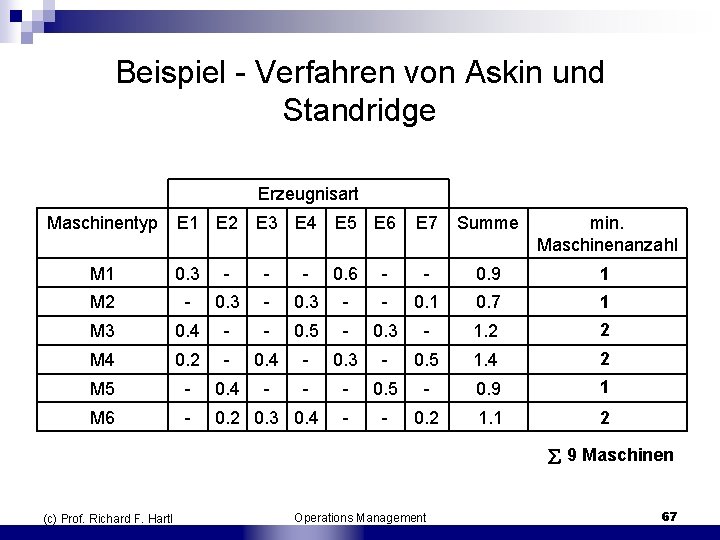
Beispiel Verfahren von Askin und Standridge Erzeugnisart Maschinentyp E 1 E 2 E 3 E 4 E 5 E 6 E 7 Summe min. Maschinenanzahl M 1 0. 3 0. 6 0. 9 1 M 2 0. 3 0. 1 0. 7 1 M 3 0. 4 0. 5 0. 3 1. 2 2 M 4 0. 2 0. 4 0. 3 0. 5 1. 4 2 M 5 0. 4 0. 5 0. 9 1 M 6 0. 2 0. 3 0. 4 0. 2 1. 1 2 9 Maschinen (c) Prof. Richard F. Hartl Operations Management 67

1. Schritt n Binäre Sortierung Erzeugnisart Maschinentyp E 1 E 5 E 7 E 3 E 4 E 6 M 4 0. 2 0. 3 0. 5 0. 4 M 3 0. 4 M 1 0. 3 0. 6 0. 5 0. 3 E 2 M 6 0. 2 0. 3 0. 4 0. 2 M 2 0. 1 0. 3 M 5 0. 5 0. 4 Lösung (c) Prof. Richard F. Hartl Operations Management 68

2. Schritt n Zuordnung der Erzeugnisse zu Maschinengruppen ¨ Benötigte Maschinen werden in die Maschinengruppe aufgenommen ¨ Weitere Erzeugnisse werden in Maschinengruppe aufgenommen, bis: n n Erreichung der Kapazitätsgrenze einer Maschine Erreichung der Höchstzahl von Maschinen in der Maschinengruppe (c) Prof. Richard F. Hartl Operations Management 69

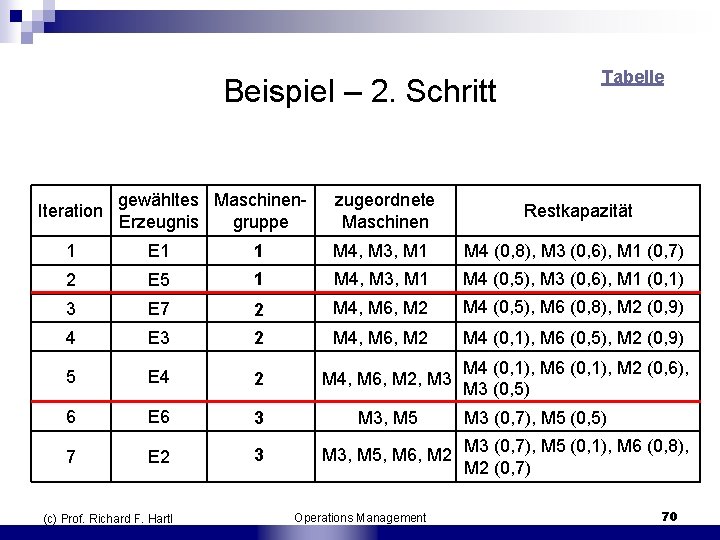
Beispiel – 2. Schritt Iteration gewähltes Maschinen Erzeugnis gruppe zugeordnete Maschinen Tabelle Restkapazität 1 E 1 1 M 4, M 3, M 1 M 4 (0, 8), M 3 (0, 6), M 1 (0, 7) 2 E 5 1 M 4, M 3, M 1 M 4 (0, 5), M 3 (0, 6), M 1 (0, 1) 3 E 7 2 M 4, M 6, M 2 M 4 (0, 5), M 6 (0, 8), M 2 (0, 9) 4 E 3 2 M 4, M 6, M 2 M 4 (0, 1), M 6 (0, 5), M 2 (0, 9) 5 E 4 2 M 4, M 6, M 2, M 3 6 E 6 3 M 3, M 5 7 E 2 3 (c) Prof. Richard F. Hartl M 4 (0, 1), M 6 (0, 1), M 2 (0, 6), M 3 (0, 5) M 3 (0, 7), M 5 (0, 5) M 3, M 5, M 6, M 2 M 3 (0, 7), M 5 (0, 1), M 6 (0, 8), M 2 (0, 7) Operations Management 70

Beispiel – Ergebnis n Benötigte Maschinen: Eine Maschine des Typs: M 1, M 5 ¨ Zwei Maschinen des Typs: M 2, M 4, M 6 ¨ Drei Maschinen des Typs: M 3 ¨ n Verfahren von Askin und Standridge: einfache Heuristik oft keine optimale Lösung n Vergleich: erhaltenes Ergebnis vs. theoretische Mindestanzahl an Maschinen event. Einsparung von je einer Maschine des Typs M 3 und M 2 möglich (c) Prof. Richard F. Hartl Operations Management 71

4. 2. 2. 1 LP Formulierung n n Zielsetzung: Minimierung der Gesamtzahl der benötigten Einzelmaschinen bei einer vorgegebenen Anzahl von Maschinengruppen Erklärung mittels vorhergehenden Beispiel Mind. 9 Maschinen erforderlich ¨ Jede Maschinengruppe höchstens M = 4 Einzelmaschinen ¨ 3 Maschinengruppen ¨ Jede Maschinengruppe enthält maximal eine einzige Maschine eines Typs ¨ (c) Prof. Richard F. Hartl Operations Management 72

Daten Kapazitätsbedarf von Erzeugnis j bezüglich Maschinentyp k Maschinengruppen bzw. Produktionsinseln Erzeugnisse Maschinentypen Höchstanzahl von Maschinen je Maschinengruppe (c) Prof. Richard F. Hartl Operations Management 73

Entscheidungsvariablen = 1, falls Erzeugnis j der Maschinengruppe i zugeordnet wird 0, sonst = 1, falls eine Maschine des Typs k der Maschinengruppe i zugeordnet wird 0, sonst (c) Prof. Richard F. Hartl Operations Management 74

Lineare Optimierung Zielfunktion: Nebenbedingungen: jedes Erzeugnis in eine Maschinengruppe Kapazität der Maschine k in Gruppe i beachten nicht mehr als M Maschine in Gruppe i binäre Variablen (c) Prof. Richard F. Hartl Operations Management 75

Lösung Maschinen gruppe Erzeugnisse 1 E 2, E 4, E 6 2 E 1, E 5 M 1, M 3, M 4 M 1 (0. 1), M 3 (0. 6), M 4 (0. 5) 3 E 3, E 7 M 2, M 4, M 6 M 2 (0. 9), M 4 (0. 1), M 6 (0. 5) n n n Maschinen Restkapazität M 2, M 3, M 5, M 6 M 2 (0. 4), M 3 (0. 2), M 5 (0. 1), M 6 (0. 4) Zulässige Konfiguration mit 10 Maschinen Optimale Lösung theoretische Mindestanzahl von 9 Maschinen aufgrund der Platzbeschränkung (M = 4) nicht erreicht (c) Prof. Richard F. Hartl Operations Management 76

4. 3 Konfiguration von Fließfertigungs Produktionssystemen n Objektprinzip n Anordnung der Arbeitssysteme orientiert sich an Arbeitsplänen der zu bearbeitenden Erzeugnisse n Bei einheitlichem Materialfluss: Arbeitssysteme werden i. d. R. linear angeordnet ¨ nur sinnvoll, wenn einheitliches Grundprodukt bzw. eine begrenzte Anzahl von Produktvarianten produziert wird ¨ (c) Prof. Richard F. Hartl Operations Management 77

4. 3. 1 Arten der Fließfertigung Nach dem zeitlichen Zusammenhang unterscheidet man 2 Formen der Fließfertigung: n Fließfertigung ohne Zeitzwang (Reihenfertigung) n Fließfertigung mit Zeitzwang (Fließbandabgleich) (c) Prof. Richard F. Hartl Operations Management 78

4. 3. 1. 1 Fließfertigung ohne Zeitzwang (Reihenfertigung) n n n Keine zeitlicher Beschränkung für die Durchführung des Arbeitsinhalt einer Station Einrichtung von Pufferlager nötig Materialfluss für alle Erzeugnisse weitgehend identisch Einzelne Arbeitsstationen können übersprungen werden; Rücksprünge nicht möglich Bearbeitungszeiten der einzelnen Produkte können sich unterscheiden (c) Prof. Richard F. Hartl Operations Management 79

4. 3. 1. 2 Fließfertigung mit Zeitzwang (Fließbandfertigung) n n getaktete Fließfertigung zeitliche Bindung zwischen den Arbeitsgängen fest vorgegebene Höchstzeit (Taktzeit) zur Bearbeitung eines Werkstückes in jeder Station Fließproduktion Selbstständige Fördereinrichtungen ¨ Einzelne Werkstücke können auch unabhängig voneinander bewegt werden (asynchroner Materialfluss) ¨ Bsp. : Montage von Fernsehern ¨ (c) Prof. Richard F. Hartl Operations Management 80

Fließbandfertigung n Verkettung zu automatisierten Gesamtsystem Transferstraße, Fließband ¨ Werkstücke sind fest mit dem Transportsystem verbunden ¨ Simultane Fortbewegung (synchroner Materialfluss) ¨ (c) Prof. Richard F. Hartl Operations Management 81

Getaktete Fließfertigung n Produktionsgeschwindigkeit = Kehrwert der Taktzeit Band kontinuierlich vorwärts bewegt Beschäftigte Personen bewegen sich während der Bearbeitung des Werkstückes parallel zum Fließband vorwärts und kehren am Ende des Taktes zum Stationsbeginn zurück n Weitere Möglichkeit: n n Band wird während Bearbeitung angehalten ¨ Werkstücke werden am Ende des Taktes zur nächsten Station weiterbewegt (intermittierender Transport) ¨ (c) Prof. Richard F. Hartl Operations Management 82

4. 3. 2 Fließbandabgleich n n Fließbandabstimmung, Fließbandaustaktung, Leistungsabstimmung, Bandabgleich Zerlegung des mehrstufigen Produktionsprozess für jedes herzustellende Produkt (Auftrag) in n Arbeitsgänge (unteilbare Elementartätigkeiten) Bearbeitungszeit tj zu jedem Arbeitsgang j Reihenfolge oder Vorrangrestriktionen möglich Vorranggraph: Zyklenfreier gerichteter Graph G = (V, E, t) ¨ Keine parallelen Pfeile oder Schlingen ¨ Für alle Pfeile (i, j) gilt die Beziehung i < j ¨ (c) Prof. Richard F. Hartl Operations Management 83

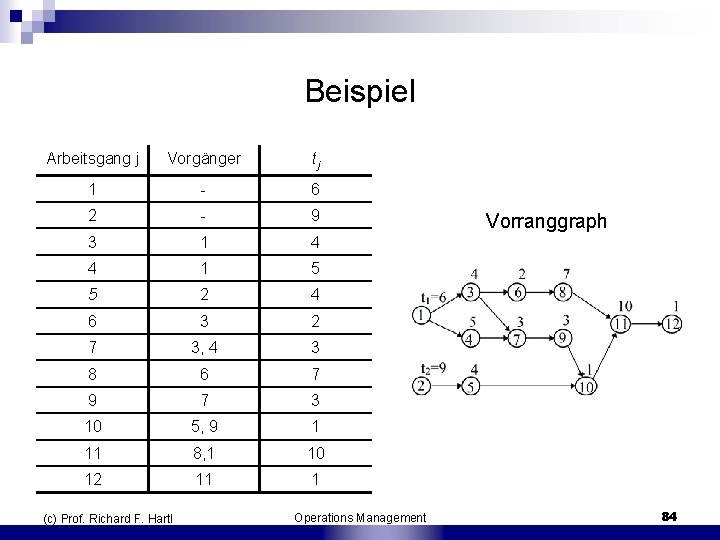
Beispiel Arbeitsgang j Vorgänger tj 1 6 2 9 3 1 4 4 1 5 5 2 4 6 3 2 7 3, 4 3 8 6 7 9 7 3 10 5, 9 1 11 8, 1 10 12 11 1 (c) Prof. Richard F. Hartl Operations Management Vorranggraph 84

Fließfertigung n n Produktiveinheiten (Maschinen) werden hintereinander angeordnet An jeder Arbeitsstation werden ein oder mehrere Arbeitsgänge ausgeführt Jeder Arbeitsgang wird genau einer Station zugeordnet (Unteilbarkeit) i vor j – (i, j) E: i und j in gleicher Station ¨ i auf früheren Station als j ¨ n Zuordnung der Arbeitsgänge zu den Stationen: zeit oder kostenorientierte Zielfunktion ¨ Einhaltung der Vorrangbeziehungen ¨ Taktzeit optimieren ¨ Gleichzeitige Bestimmung von Stationszahl und Taktzeit ¨ (c) Prof. Richard F. Hartl Operations Management 85

4. 3. 3 Einproduktmodelle n „klassisches Modell der Fließbandabstimmung“ n Simple assembly line balancing problem (c) Prof. Richard F. Hartl Operations Management 86

4. 3. 3. 1 Ein Grundmodell mit alternativen Zielsetzungen Annahmen: n n n n n Herstellung eines homogenen Produktes in n Arbeitsgängen vorgegebene Bearbeitungszeiten ti für die Arbeitsgänge j = 1, . . . , n Reihenfolgebeziehungen (Vorranggraphen) alle Stationen besitzen dieselbe Taktzeit fixe Anstoßrate gleichwertig ausgestattete Stationen (hinsichtlich Personal und Betriebsmittel) keine parallelen Stationen geschlossene Stationen unbewegliche Werkstücke (c) Prof. Richard F. Hartl Operations Management 87

4. 3. 3. 1. 1 Alternative 1 Minimierung der Stationsanzahl m bei vorgegebener Taktzeit c: n untere Schranke für die Stationszahl n obere Schranke für die Stationszahl (c) Prof. Richard F. Hartl Operations Management 88

Beweis t(Sk) … Belegungszeit der Stationen Sk, k = 1, . . . , m Ganzzahligkeit tmax + t(Sk) > c also t(Sk) c + 1 tmax k =1, . . . , m 1 Summieren der Ungleichungen und Ganzzahligkeit von m obere Schranke (c) Prof. Richard F. Hartl Operations Management 89

4. 3. 3. 1. 2 Alternative 2 Minimierung der Taktzeit (bzw. Maximierung der Produktionsgeschwindigkeit) untere Schranken für die Taktzeit c: n n n tmax = max {tj j = 1, . . . , n} … Dauer des längsten Arbeitsganges Unteilbarkeit der Arbeitsgänge c tmax Produktions bzw. Absatzhöchstmenge qmax im Planungszeitraum der Länge T vorgegeben Mit Hilfe der gegebenen Stationsanzahl m (c) Prof. Richard F. Hartl Operations Management 90

Alternative 2 n untere Schranke für die Taktzeit (insgesamt) n obere Schranke für die Taktzeit (c) Prof. Richard F. Hartl Operations Management 91

4. 3. 3. 1. 3. Alternative 3 Maximierung des Bandwirkungsgrades (BG) n Bestimmung von: positiver Taktzeit c ¨ positiver Stationszahl m ¨ um BG (Auslastung des Fließbandes) zu maximieren n BG = 1 Auslastung von 100% (keine Leerzeiten) (c) Prof. Richard F. Hartl Operations Management 92

Alternative 3 n untere Schranke für die Taktzeit wie bei Alternative 2 obere Schranke für die Taktzeit cmax gegeben n untere Schranke für die Stationszahl n obere Schranke für die Stationszahl n (c) Prof. Richard F. Hartl Operations Management 93

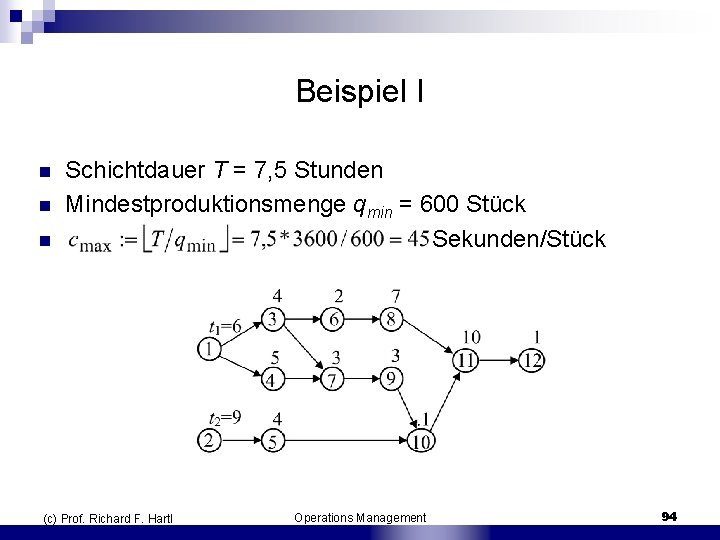
Beispiel I n n n Schichtdauer T = 7, 5 Stunden Mindestproduktionsmenge qmin = 600 Stück Sekunden/Stück (c) Prof. Richard F. Hartl Operations Management 94

Beispiel II Arbeitsgang j Vorgänger tj 1 6 2 9 3 1 4 4 1 5 5 2 4 6 3 2 7 3, 4 3 8 6 7 9 7 3 10 5, 9 1 11 8, 1 10 12 11 1 Summe 55 (c) Prof. Richard F. Hartl tj = 55 keine Absatzhöchstmenge Taktzeit mindestens cmin = tmax = 10 Sekunden/Stück Operations Management 95

Beispiel III Alle Kombinationen von m und c, für die eine zulässige Lösung des Problems existiert (c) Prof. Richard F. Hartl Operations Management 96

Beispiel IV n maximaler BG = 1 (nur für unzulässige Werte: m = 1 und c = 55 erreichbar) n Optimaler BG = 0, 982 (zulässiger Bereich: 10 c 45 und m 2) m = 2 Stationen c = 28 Sekunden/Stück (c) Prof. Richard F. Hartl Operations Management 97

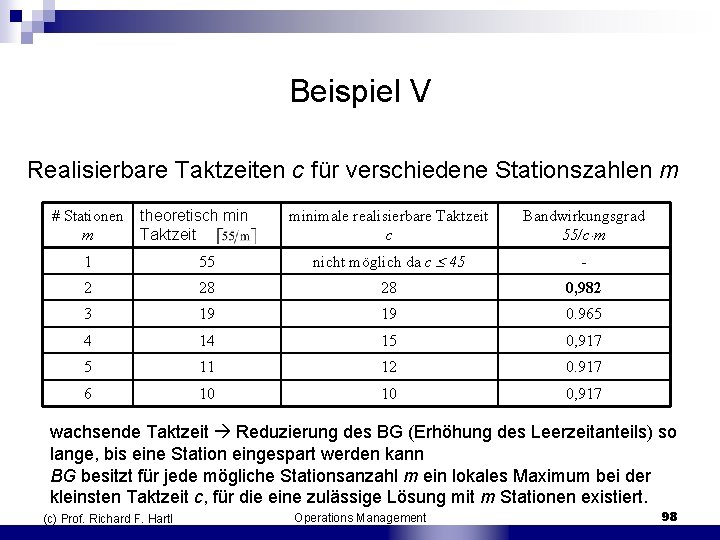
Beispiel V Realisierbare Taktzeiten c für verschiedene Stationszahlen m # Stationen m theoretisch min Taktzeit minimale realisierbare Taktzeit c Bandwirkungsgrad 55/c m 1 55 nicht möglich da c 45 - 2 28 28 0, 982 3 19 19 0. 965 4 14 15 0, 917 5 11 12 0. 917 6 10 10 0, 917 wachsende Taktzeit Reduzierung des BG (Erhöhung des Leerzeitanteils) so lange, bis eine Station eingespart werden kann BG besitzt für jede mögliche Stationsanzahl m ein lokales Maximum bei der kleinsten Taktzeit c, für die eine zulässige Lösung mit m Stationen existiert. (c) Prof. Richard F. Hartl Operations Management 98

4. 3. 3. 1. 4 Weitere Zielsetzungen für das Grundmodell Maximierung des BG ist äquivalent zu: n Minimierung der Durchlaufzeit: n Minimierung der Summe der Leerzeiten: n Minimierung des Leerzeitanteils: n Minimierung der Gesamtwartezeit: (c) Prof. Richard F. Hartl Operations Management D = m c LA = = 1 – BG 99

4. 3. 4 LP Formulierungen Unterscheidung zwischen: n LP Formulierung bei gegebener Taktzeit n LP Formulierung bei gegebener Stationszahl n Mathematische Formulierung bei Maximierung des Bandwirkungsgrades (c) Prof. Richard F. Hartl Operations Management 100

4. 3. 4. 1 LP Formulierung bei gegebener Taktzeit n Binärvariablen: j = 1, . . . , n k = 1, . . . , mmax n = Nummer der Station, der Arbeitsgang j zugeordnet ist n Annahme: Graph G besitzt Knoten n als einzige Senke (c) Prof. Richard F. Hartl Operations Management 101

Modellformulierung Zielfunktion: Nebenbedingungen: (c) Prof. Richard F. Hartl j = 1, . . . , n . . . AG auf genau eine Station k = 1, . . . , mmax . . . Einhaltung der Taktzeit bei Station k . . . Vorrangbeziehungen j und k . . . binäre Variablen Operations Management 102

Bemerkungen Mögliche Erweiterungen: n Zuordnungseinschränkungen in Form von Betriebsmittel oder Positionsrestriktionen ¨ n entsprechende Variablen aus dem Modell entfernen oder vorab zu Null fixieren Arbeitsgangrestriktionen ¨ Verhinderung, dass zwei Arbeitsgänge h und j mit (h, j) in derselben Station ausgeführt werden (c) Prof. Richard F. Hartl Operations Management 103

4. 3. 4. 2 LP Formulierung bei gegebener Stationszahl n Ersetzen vom mmax durch gegebene Stationszahl m n c wird zusätzliche Variable (c) Prof. Richard F. Hartl Operations Management 104

Modellformulierung Zielfunktion: Minimiere Z(x, c) = c Nebenbedingungen: … Taktzeit c 0 ganzzahlig j = 1, . . . , n . . . AG auf genau eine Station k = 1, . . . , m . . . Einhaltung der Taktzeit bei Station k . . . Vorrangbeziehungen j und k . . . binäre Variablen (c) Prof. Richard F. Hartl Operations Management 105

4. 3 Mathematische Formulierung bei Maximierung des Bandwirkungsgrades n Ist weder Taktzeit c noch Stationszahl m gegeben übernehmen der LP Formulierung bei gegebener Taktzeit Zielfunktion (nichtlinear): zusätzlichen Nebenbedingungen: c cmax c cmin (c) Prof. Richard F. Hartl Operations Management 106

Mathematische Formulierung bei Maximierung des Bandwirkungsgrades n Wiedererlangen eines LPs Gewichtung von Taktzeit und Stationsanzahl mit den Faktoren w 1 und w 2 Zielfunktion (linear): Minimiere Z(x, c) = w 1 ( k xnk) + w 2 c sehr große LP Modelle hohe Anzahl von Binärvariablen (c) Prof. Richard F. Hartl Operations Management 107

4. 3. 5. Heuristische Verfahren bei gegebener Taktzeit n Zahlreiche heuristische Verfahren (zumeist Prioritätsregelverfahren) n Verkürzte exakte Verfahren n enumerative Vorgehensweise (c) Prof. Richard F. Hartl Operations Management 108

Prioritätsregelverfahren I n Zuordnung eines Rangwerts RWj zu jedem Arbeitsgang j n Prioritätsliste n Ein noch nicht zugeordneter Arbeitsgang j ist in einer Station k einplanbar, falls alle seine Vorgänger im Vorranggraphen in einer der Stationen 1, . . . , k bereits eingeplant sind und ¨ die aktuelle Leerzeit der Station k nicht kleiner als die Bearbeitungszeit von j ist. ¨ (c) Prof. Richard F. Hartl Operations Management 109

Prioritätsregelverfahren II n Vorraussetzung: Taktzeit c ¨ einzuplanende Arbeitsgänge j=1, . . . , n mit Bearbeitungszeiten tj c ¨ Vorranggraph, gegeben durch Vorgängermengen V(j) ¨ n Variablen k ¨ ¨ Lp ¨ Ls ¨ (c) Prof. Richard F. Hartl Nummer der aktuellen Station Leerzeit der aktuellen Station Liste bisher eingeplanter Arbeitsgänge Sortierte Liste der n Arbeitsgänge gemäß Prioritätsregel Operations Management 110

Prioritätsregelverfahren III n Ein Arbeitsgang j Lp ist einplanbar, wenn tj und h Lp für alle h V(j) gilt n stationsweise vorgehen n unter den jeweils einplanbaren Arbeitsgängen wird derjenige mit höchster Priorität zugeordnet n Öffnung einer neue Station, wenn die aktuell betrachtete Station maximal belegt ist (c) Prof. Richard F. Hartl Operations Management 111

Prioritätsregelverfahren IV Start: bestimme Liste Ls mit Hilfe einer Prioritätsregel; k : = 0; LP : = <]; . . . noch nichts einge plant Iteration: repeat k : = k+1; : = c; while es existiert für Station k einplanbarer Arbeitsgang in der Liste Ls do begin wähle und entferne den ersten einplanbaren Arbeitsgang j aus Liste Ls; Lp: = < Lp, j]; : = tj end; until Ls = <]; Ergebnis: Lp enthält eine zulässige Reihung der Aufträge mit m = k Stationen. Single-Pass vs. Multi-Pass-Heuristiken (je nachdem ob Verfahren ein oder mehrmalig durchlaufen wird) (c) Prof. Richard F. Hartl Operations Management 112

Prioritätsregeln I n Regel 1: Zufällige Auswahl von Arbeitsgängen n Regel 2: Wähle die Arbeitsgänge nach monoton abnehmender (oder zunehmender) Bearbeitungszeit tj aus: RWj: = tj n Regel 3: Wähle die Arbeitsgänge nach monoton abnehmender (oder zunehmender) Zahl der unmittelbaren Nachfolger aus: RWj : = (j) n Regel 4: Wähle die Arbeitsgänge nach monoton wachsender Tiefe der Arbeitsgänge in G aus: RWj : = Anzahl Pfeile im Weg mit den meisten Pfeilen von einer Quelle des Vorranggraphen nach j (c) Prof. Richard F. Hartl Operations Management 113

Prioritätsregeln II n Regel 5: Wähle die Arbeitsgänge nach monoton abnehmendem Positionsgewicht (Positionswert): n Regel 6: Wähle die Arbeitsgänge nach monoton zunehmender oberer Schranke der für j und alle Vorgänger benötigten Stationszahl aus: n Regel 7: Wähle die Arbeitsgänge nach monoton zunehmender oberer Schranke für die spätestmögliche Station des Arbeitsganges j aus: (c) Prof. Richard F. Hartl Operations Management 114

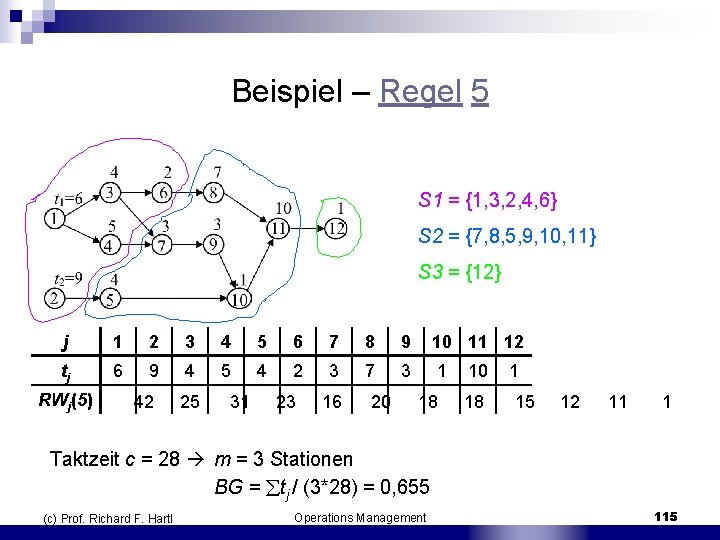
Beispiel – Regel 5 S 1 = {1, 3, 2, 4, 6} S 2 = {7, 8, 5, 9, 10, 11} S 3 = {12} j 1 2 3 4 5 6 7 8 9 10 11 12 tj 6 9 4 5 4 2 3 7 3 1 RWj(5) 42 25 31 23 16 20 18 1 15 12 11 1 Taktzeit c = 28 m = 3 Stationen BG = tj / (3*28) = 0, 655 (c) Prof. Richard F. Hartl Operations Management 115

Beispiel – Regel 7, 6 und 2 n = 3 j 1 2 3 4 5 6 7 8 9 10 11 12 RWj(7) 1 2 2 2 2 2 RWj(6) 1 1 1 1 1 2 2 2 RWj(2) 6 9 4 5 4 2 3 7 3 1 10 1 Anwendung von: primär Regel 7 (spätmöglichste Station) bei Gleichheit Regel 6 (für j und alle Vorgänger benötigten Stationszahl) bei Gleichheit Regel 2 (nach abnehmenden tj) Lösung: c = 28 m = 2; BG = 0, 982 S 1 = {1, 3, 2, 4, 5} ; S 2 = {7, 9, 6, 8, 10, 11, 12} (c) Prof. Richard F. Hartl Operations Management 116

Weitere heuristische Verfahren I n Stochastische Varianten der Prioritätsregeln 2 bis 7: zufällige Auswahl des nächsten Arbeitsganges unter den einplanbaren Arbeitsgängen ¨ Auswahlwahrscheinlichkeiten: proportional oder umgekehrt proportional zu Rangwerten ¨ Zufällig ermittelte Prioritätsregel ¨ n Enumerative Heuristiken: Ermittlung sämtlicher zulässiger Belegungen für erste Station ¨ Einplanung der Stationsbelegung mit geringster Leerzeit ¨ Analoge Bildung der weiteren Stationen (Greedy) ¨ (c) Prof. Richard F. Hartl Operations Management 117

Weitere heuristische Verfahren II n Heuristiken von Verschnitt und Verpackungsproblemen zusätzliche Beachtung der Vorrangbeziehungen ¨ z. B. : Verallgemeinerung der Heuristik First Fit Decreasing für das Bin Packing Problem ¨ n Kürzeste Wege Problem mit exponentiell vielen Knoten n Vertauschungsverfahren: Austauschen von Arbeitsgängen zwischen Stationen ¨ Ziel: Verbesserung des nachgeordneten Ziels einer möglichst gleichmäßigen Stationsauslastung ¨ (c) Prof. Richard F. Hartl Operations Management 118

Worst Case Analyse von Heuristiken Lösungseigenschaften bei Ganzzahligkeit von c und tj (j = 1, . . . , n) für Alternative 2: Summe der Belegungszeiten zweier benachbarter Stationen müssen die Taktzeit überschreiten Worst Case Schranken für die Abweichung einer Lösung mit m Stationen von einer optimalen Lösung mit m* Stationen: m/m* 2 2/m* für gerades m bzw. m/m* 2 1/m* für ungerades m m < c m*/(c - tmax + 1) + 1 (c) Prof. Richard F. Hartl Operations Management 119

4. 3. 6 Verfahren zur Bestimmung der Taktzeit n gegebene Stationszahl n Taktzeit nicht gegeben Taktzeit ist zu minimieren (Alternative 1) oder ¨ Taktzeit ist gemeinsam mit der Stationszahl zu optimieren um einen maximalen BG zu erzielen (Alternative 3) ¨ (c) Prof. Richard F. Hartl Operations Management 120

Iteratives Verfahren zur Ermittlung der minimalen Taktzeit I 1. Ermittle die theoretische minimale Taktzeit (bzw. cmin = tmax wenn dies größer ist) und setze c = cmin 2. Suche für die Taktzeit c eine optimale Lösung mit minimaler Stationszahl m(c) mittels Verfahren zu Alternative 1 (vgl. 2. 3. 2. und 2. 3. 3. ) 3. Wenn m(c) größer als die gegebene Stationszahl: vergrößere c um (ganzzahlig) und wiederhole Schritt 2. (c) Prof. Richard F. Hartl Operations Management 121

Iteratives Verfahren zur Ermittlung der minimalen Taktzeit II n Zulässige Lösung mit Taktzeit c und Stationszahl m gefunden. n Wenn > 1, so kann man noch eine Intervallschachtelung vornehmen: wenn also für Taktzeit c eine Lösung mit Stationszahl m gefunden wurde und für Taktzeit c nicht, so kann man noch c /2 probieren, etc. (c) Prof. Richard F. Hartl Operations Management 122

Beispiel – Regel 5 m = 5 Stationen Suche: maximal mögliche Produktionsrate minimale Taktzeit j 1 2 3 4 5 6 7 8 9 10 11 12 tj 6 9 4 5 4 2 3 7 3 1 10 1 RWj(5) 42 25 31 23 16 20 18 18 15 12 11 1 Es muss mindestens die Taktzeit cmin = tj/m = 55/5 = 11 gewählt werden (es ist 11 > tmax = 10) (c) Prof. Richard F. Hartl Operations Management 123

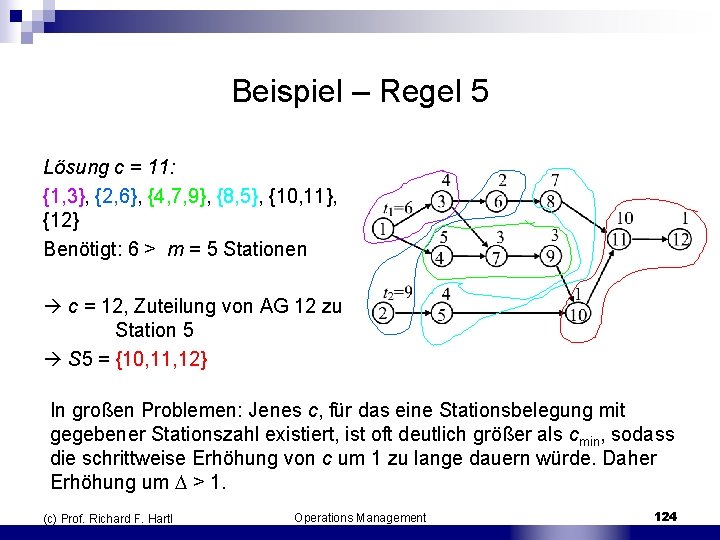
Beispiel – Regel 5 Lösung c = 11: {1, 3}, {2, 6}, {4, 7, 9}, {8, 5}, {10, 11}, {12} Benötigt: 6 > m = 5 Stationen c = 12, Zuteilung von AG 12 zu Station 5 S 5 = {10, 11, 12} In großen Problemen: Jenes c, für das eine Stationsbelegung mit gegebener Stationszahl existiert, ist oft deutlich größer als cmin, sodass die schrittweise Erhöhung von c um 1 zu lange dauern würde. Daher Erhöhung um > 1. (c) Prof. Richard F. Hartl Operations Management 124

4. 3. 7 Klassifikation von komplexeren Fließbandabstimmungsproblemen Überlegungen bezüglich: n Anzahl der Produkte n Zuordnungsrestriktionen n Parallele Stationen n Ausstattung von Stationen mit Arbeitskräften n Stationsbegrenzung n Anstoßrate n Verbindung der Werkstücke zum Transportsystem n Verfahrensalternativen n Zielsetzungen (c) Prof. Richard F. Hartl Operations Management 125

4. 3. 7. 1 Anzahl der Produkte n Einproduktmodelle: Fertigung eines homogenen Produkts auf einem Fließband ¨ Massenproduktion, Großserienfertigung ¨ n Mehrproduktmodelle: Gemeinsame Fertigung mehrerer Produkte auf einem oder mehreren Fließbändern ¨ Arten: ¨ n n Varianten Fließfertigung: Produkte sind Varianten eines Grundproduktes Bearbeitung in gemischter Folge auf dem Fließband losweise Mehrprodukt Fließfertigung: Umrüstvorgänge zwischen der Fertigung von verschiedenen Produkten Produktionslose (jedes Produkt hat eigene Fließbandaustaktung) Planung von Losgrößen und Reihenfolge der einzelnen Produkte TSP (c) Prof. Richard F. Hartl Operations Management 126

4. 3. 7. 2 Zuordnungsrestriktionen n Betriebsmittelrestriktionen: Ausrüstung einer bestimmten Station mit geeigneten Betriebsmittel nötig ¨ vorgegebene Umgebungsbedingungen ¨ n Positionsrestriktionen: ¨ n Arbeitsgangrestriktionen: ¨ n Festlegung der Position eines Werkstücks innerhalb der Station bestimmte AG nicht ausführbar (z. B. : Unterbodenarbeiten) zeitliche oder räumliche Mindest oder Maximalabstände zwischen 2 AG bestimme Arbeitsgangkombinationen an derselben Station nicht ausführbar Qualifikationsrestriktionen: ¨ Kombination von Arbeitsgängen mit ähnlichem Anspruchsniveau (c) Prof. Richard F. Hartl Operations Management 127

4. 3. 7. 3. Parallele Stationen n Modelle ohne parallelen Stationen: ¨ n Heterogene Stationen mit unterschiedlicher Zuordnung von AG serielles Fließband Modelle mit parallelen Stationen: Mindestens 2 Stationen, dieselben AG ausführen ¨ Bearbeitung von aufeinanderfolgenden Aufträgen auf zueinander parallelen Stationen im zeitlichen Wechsel ¨ n Mischform Parallelisierung von Arbeitsgängen: Zuordnung eines AG zu zwei verschiedenen Stationen eines seriellen Fließbandes ¨ Ausführung des AG abwechselnd in einer der beiden Stationen ¨ (c) Prof. Richard F. Hartl Operations Management 128

4. 3. 7. 4 Ausstattung von Stationen mit Arbeitskräften n Einfachbemannte Stationen: ¨ n Eine Arbeitskraft pro Station Mehrfachbemannung: Differenzierung der Arbeitsinhalte der Stationen möglich ¨ Kurzfristige Kapazitätsanpassung durch flexiblen Einsatz von Springern ¨ n Vollautomatisierte Stationen: Einsatz von Arbeitskräften zur Kontrolle des Fertigungsprozesses ¨ Oft für mehrere Stationen zuständig ¨ (c) Prof. Richard F. Hartl Operations Management 129

4. 3. 7. 5 Stationsbegrenzung n Geschlossene Stationen: räumliche Ausdehnung für Station fest vorgegeben ¨ Verlassen des Bereichs während der Bearbeitung nicht erlaubt ¨ n Offene Stationen: ¨ Stationsgrenzen dürfen in/oder entgegen der Fließrichtung verlassen werden n n rechtsoffen (in Fließrichtung verlassen) linksoffen (entgegen der Fließrichtung verlassen) kurzfristige Kapazitätsanpassung durch Unter bzw. Überschreitung der (lokalen) Taktzeit ¨ z. B. : Herstellung von Produktvarianten ¨ (c) Prof. Richard F. Hartl Operations Management 130

4. 3. 7. 6 Anstoßrate n Modelle mit fixer Anstoßrate: ¨ n Aufeinanderfolgende Werkstücke werden jeweils nach Ablauf derselben Zeitspanne (Auflageintervall) auf das Fließband gebracht Modelle mit variabler Anstoßrate: Das nächste Werkstück wird eingelastet, sobald die erste Bandstation wieder frei ist. ¨ Unterschiedliche Abstände der Werkstücke auf dem Fließband (bei Mehrproduktfertigung) ¨ (c) Prof. Richard F. Hartl Operations Management 131

4. 3. 7. 7 Verbindung der Werkstücke zum Transportsystem n Unbewegliche Werkstücke: fest mit dem Transportsystem verbunden ¨ allenfalls Drehbewegungen erlaubt ¨ n Bewegliche Werkstücke: ¨ Zwischenzeitliche Wegnahme vom Transportsystem erlaubt n n ¨ Nachbearbeitung Zwischenlagerung Fließfertigung ohne Zeitzwang (c) Prof. Richard F. Hartl Operations Management 132

4. 3. 7. 8 Verfahrensalternativen n Vorgegebene Produktionsverfahren ¨ n Arbeitspläne sind vorgegeben Verschiedene Produktionsverfahren Wahl bezüglich des einzusetzenden Verfahrens ¨ Mehrere alternative Arbeitspläne vorhanden (Vorranggraphen) ¨ und/oder ¨ unterschiedliche Bearbeitungszeiten einzelner Arbeitsgänge (c) Prof. Richard F. Hartl Operations Management 133

4. 3. 7. 9 Zielsetzungen n Zeitorientierte Zielsetzungen Minimierung der Durchlaufzeit, der Gesamtleerzeit, des Leerzeitanteils, der Gesamtwartezeit ¨ Maximierung der Kapazitätsauslastung (Bandwirkungsgrad) – bei den meisten (Einprodukt ) Modellen ¨ Gleichmäßige Auslastung der Stationen ¨ n Weitere Zielsetzungen Minimierung der Stationsanzahl bei geg. Taktzeit ¨ Minimierung der Taktzeit bei geg. Stationszahl ¨ Minimierung der Summe der gewichteten Taktzeit und der gewichteten Stationszahl ¨ (c) Prof. Richard F. Hartl Operations Management 134

Zielsetzungen n Erfolgsorientierte Ansätze: Maximierung des Gesamtdeckungsbeitrags ¨ Minimierung der Gesamtkosten ¨ n n Maschinen und Werkzeugkosten (Maschinenstundensätze – von Stationsanzahl abhängig) Lohnkosten: häufig identische Lohnsätze für die Arbeitskräfte aller Stationen Materialkosten: durch Ausbringungsmenge und Taktzeit bestimmt Leerkosten: Opportunitätskosten – hängen von Taktzeit und Stationsanzahl ab (c) Prof. Richard F. Hartl Operations Management 135

4. 3. 8 Mehrproduktmodelle n n n Variantenfließfertigung: Bearbeitung mehrere Varianten eines Grundmodells in gemischter Folge auf einem Fließband einzelne Arbeitsgänge können von Variante zu Variante unterschiedliche Bearbeitungszeiten aufweisen einzelne Arbeitsgänge nicht bei allen Varianten erforderlich Bestimmung einer optimalen Abstimmung des Fließbandes und einer optimalen Bearbeitungsreihenfolge für die Werkstücke (c) Prof. Richard F. Hartl Operations Management 136

n n n multi-model losweise Mehrprodukt Fließfertigung mit Umrüsten (c) Prof. Richard F. Hartl Umrüsten von Würfel auf Pyramide nach 2 Wochen Operations Management 137

n n mixed model Varianten fließfertigung ohne Umrüsten Abstimmung auf eine „theoretische Durchschnitts variante“ (c) Prof. Richard F. Hartl Operations Management 138

4. 3. 9 Fließbandabstimmung bei Variantenfertigung n Bei ähnlichen Varianten: Vermeidung von Umrüstung und Losbildung ¨ Betrachtung aller Varianten simultan (Varianten-Fließfertigung) ¨ n Verallgemeinerung des Grundmodells (von 2. 3. 1) ¨ ¨ ¨ Herstellung von p Varianten eines Grundproduktes in bis zu n Arbeitsgängen; das Produktionsverfahren ist fest vorgegebene Reihenfolgebeziehungen für die Arbeitsgänge in jeder Variante j = 1, . . . , n gemeinsamen Vorrangsgraphen über alle Varianten aggregieren jeder AG wird genau einer Station zugeordnet vorgegebene Bearbeitungszeiten tjv jedes AG j bei jeder Variante v gegebener Bedarf bv bei jeder Variante v gegebene Gesamtdauer T der Arbeitsschichten im Planungszeitraum (c) Prof. Richard F. Hartl Operations Management 139

Fließbandabstimmung bei Variantenfertigung n Gesamtbedarf aller Varianten im Planungszeitraum: n Kumulierte Bearbeitungszeit von AG j über alle Varianten im Planungszeitraum: (c) Prof. Richard F. Hartl Operations Management 140

LP Modell n Aggregierte Variante: ¨ n Fließband wird nicht taktweise, sondern auf Grundlage der Gesamtdauer T der Arbeitsschichten im Planungszeitraum abgestimmt Gleiche LP wie im Kapitel 2. 3. 1. 5, jedoch ¨ Ersetzen der Taktzeit c durch die Gesamtdauer T (c) Prof. Richard F. Hartl Operations Management 141

LP Modell Zielfunktion: … Nummer der letzten Station (mit AG n) Nebenbedingungen: (c) Prof. Richard F. Hartl für alle j = 1, . . . , n . . . AG auf genau eine Station für alle k = 1, . . . , . . . Gesamtdauer bei Station k für alle . . . Vorrangbeziehungen für alle j und k Operations Management 142

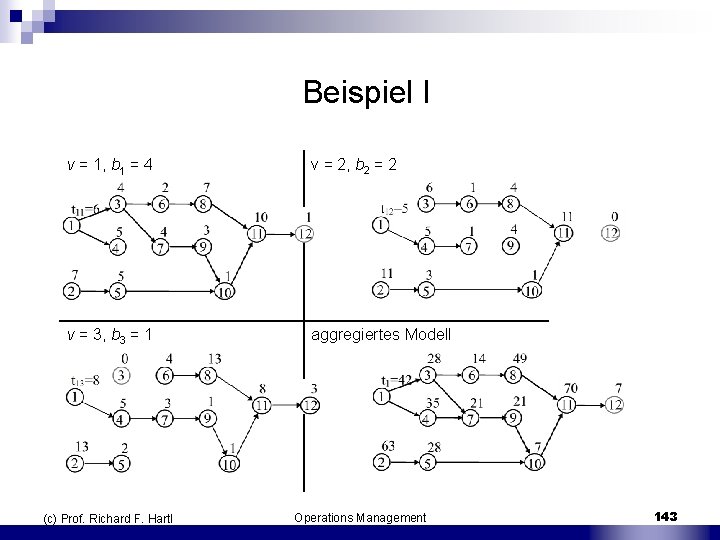
Beispiel I v = 1, b 1 = 4 v = 2, b 2 = 2 v = 3, b 3 = 1 aggregiertes Modell (c) Prof. Richard F. Hartl Operations Management 143

Beispiel II Verwendung von exakten Verfahren: n gegeben: T = 70 n Stationszuteilung mit m = 7 Stationen: S 1 = {1, 3} S 2 = {2} S 3 = {4, 6, 7} S 4 = {8, 9} S 5 = {5, 10} S 6 = {11} S 7 = {12} (c) Prof. Richard F. Hartl Operations Management 144

Größen. . . Belegungszeit der Station k durch Variante v in Zeitdauer T . . . mittlere Belegungszeit der m Stationen durch Variante v in T bzw. die analogen Größen pro Stück (ME): . . . Belegungszeit der Station k durch 1 ME von Variante v . . . mittlere Belegungszeit der m Stationen durch 1 ME Variante v Aggregiert über alle Varianten erhält man: . . . (c) Prof. Richard F. Hartl gesamte Belegungszeit der Station k in T Operations Management 145

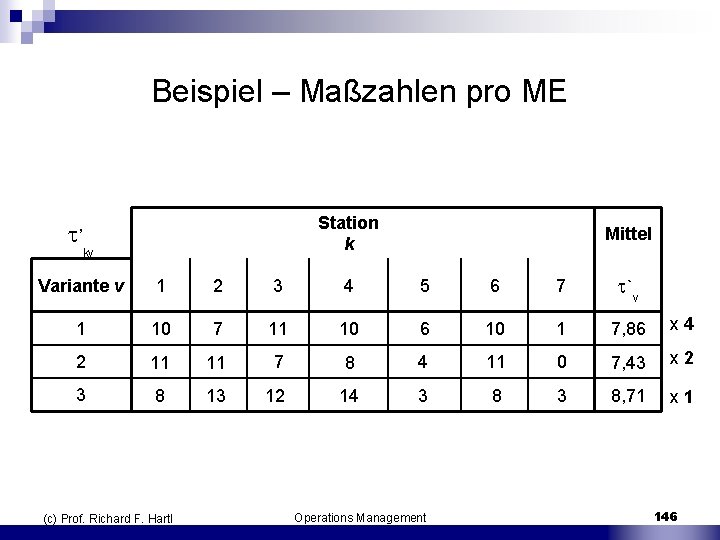
Beispiel – Maßzahlen pro ME Station k Mittel Variante v 1 2 3 4 5 6 7 `v 1 10 7 11 10 6 10 1 7, 86 x 4 2 11 11 7 8 4 11 0 7, 43 x 2 3 8 13 12 14 3 8, 71 x 1 ’ kv (c) Prof. Richard F. Hartl Operations Management 146

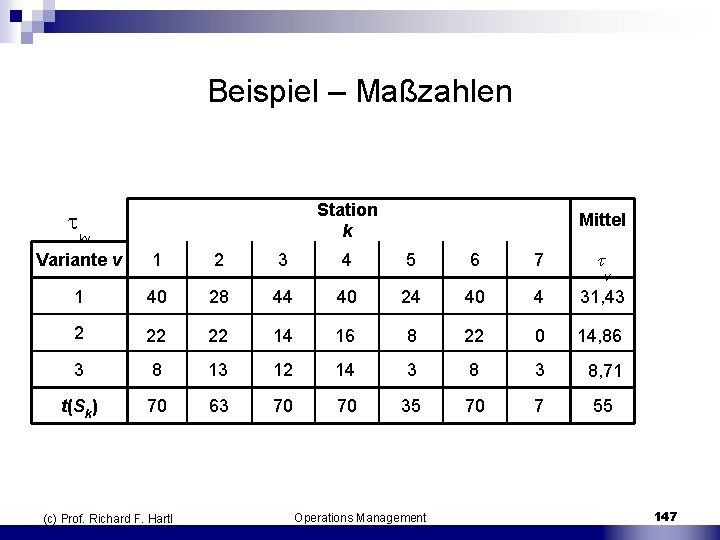
Beispiel – Maßzahlen Station k Mittel 1 2 3 4 5 6 7 kv Variante v v 1 40 28 44 40 24 40 4 31, 43 2 22 22 14 16 8 22 0 14, 86 3 8 13 12 14 3 8, 71 t(Sk) 70 63 70 70 35 70 7 55 (c) Prof. Richard F. Hartl Operations Management 147

Fazit n Station 5 und 7 sind sehr schlecht ausgelastet n die Belegungszeiten kv der Stationen k schwanken bei den Varianten v stärker als die aggregierte Variante t(Sk) n Die Belegungszeiten schwanken bei den Größen pro ME (2. Tabelle) stark mit der Variante. Bei Variante 3 sind z. B. die Stationen 2, 3 und 4 sehr stark beansprucht. ¨ mehrere ME von Variante 3 hintereinander gefertigt die mittlere Taktzeit kann hier nicht eingehalten werden, d. h. das Band muss angehalten werden. (c) Prof. Richard F. Hartl Operations Management 148

Behebung der ungleichen Auslastungen n durch Betrachtung nachgeordneter Zielfunktionen ¨ Unter mehreren Lösungen, die alle die gleiche (minimale) Stationszahl m liefern (1. Ziel), wählt man jene, die folgende 2. Zielfunktion minimiert: . . . ¨ Summe der absoluten Auslastungsunterschiede Minimierung z. B. durch folgende Greedy Heuristik möglich (c) Prof. Richard F. Hartl Operations Management 149

Verfahren von Thomopoulos Start: Abweichung = 0, k = 0 Iteration: solange noch nicht alle AG eingeplant: erhöhe k um 1 ermittle alle zulässigen Stationsbelegungen Sk für die nächste Station k wähle jenes Sk mit der kleinsten Abweichungssumme setze = + (Sk) (c) Prof. Richard F. Hartl Operations Management 150

Verfahren von Thomopoulos – Beispiel T = 70 m = 7 Lösung: 9 Stationen (min. Stationszahl = 7): S 1 = {1}, S 2 = {3, 6}, S 3 = {4, 7}, S 4 = {8}, S 5 = {2}, S 6 = {5, 9}, S 7 = {10}, S 8 = {11}, S 9 = {12} Abweichungssumme: = 183, 14 (c) Prof. Richard F. Hartl Operations Management 151

Verfahren von Thomopoulos n Nur jene Stationsbelegungen Sk kommt in Frage, deren Belegungszeit t(Sk) einen Wert überschreiten (keine zu großen Leerzeiten). n Wahl von : ¨ zu klein: n n ¨ sehr ausgeglichene Stationsbelegungen bezüglich der einzelnen Varianten u. U. zu viele Stationen. zu groß: n n wenig ausgeglichene Stationsbelegungen eher minimale Stationszahl. [sehr großes u. U. gar keine zulässige Stationsbelegung mit t(Sk) ] (c) Prof. Richard F. Hartl Operations Management 152

Verfahren von Thomopoulos – Beispiel Fort. = 49 Lösung: 7 Stationen: S 1 = {2}, S 2 = {1, 5}, S 3 = {3, 4}, S 4 = {7, 9, 10}, S 5 = {6, 8}, S 6 = {11}, S 7 = {12} Abweichungssumme: = 134, 57 (c) Prof. Richard F. Hartl Operations Management 153

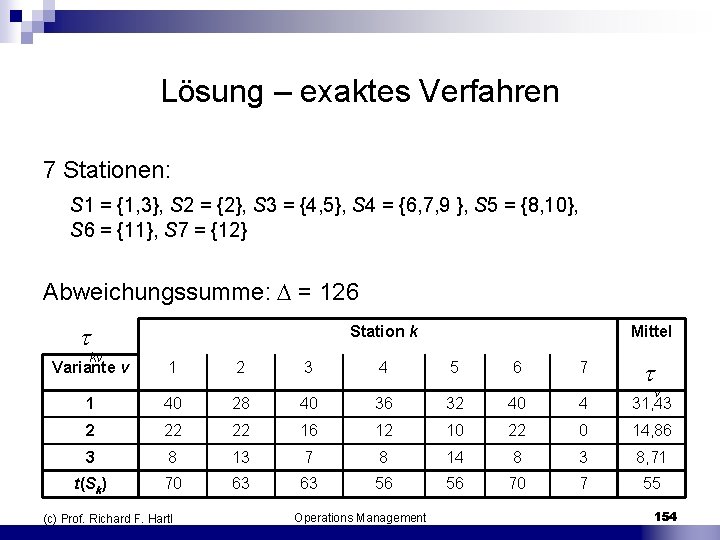
Lösung – exaktes Verfahren 7 Stationen: S 1 = {1, 3}, S 2 = {2}, S 3 = {4, 5}, S 4 = {6, 7, 9 }, S 5 = {8, 10}, S 6 = {11}, S 7 = {12} Abweichungssumme: = 126 Station k Mittel Variante v 1 2 3 4 5 6 7 1 40 28 40 36 32 40 4 31, 43 2 22 22 16 12 10 22 0 14, 86 3 8 13 7 8 14 8 3 8, 71 t(Sk) 70 63 63 56 56 70 7 55 kv (c) Prof. Richard F. Hartl Operations Management v 154

Weitere Zielsetzungen n Abstimmung von Nachfragewerten bj abhängig Änderung der Nachfragewerte Abstimmung wiederholen und umrüsten n Umgehen durch: n ¨ Nachfrageunabhängige Zielsetzungen … Summe der absoluten Auslastungsunterschiede pro Stück (c) Prof. Richard F. Hartl Operations Management 155

Weitere Zielsetzungen n Nachteil dieser Zielfunktionen: ¨ Große Abweichungen bei einer Station (die zu Störungen im Produktionsablauf führen können) können durch geringe Abweichungen bei einigen anderen Stationen kompensiert werden. . . . maximaler Auslastungsunterschied pro Stück (ME) (c) Prof. Richard F. Hartl Operations Management 156

4. 4 Konfiguration von Lagerhäusern n einfaches Modell von Askin & Standridge (c) Prof. Richard F. Hartl Operations Management 157

4. 5 Konfiguration und Analyse von flexiblen Fließfertigungssystemen n einfache Warteschlangenmodelle, M/M/s, M/G/1, GI/G/1 n aus Zeitgründen werden diese Themen hier nicht behandelt; (c) Prof. Richard F. Hartl Operations Management 158