Kapasitansi Kapasitor plat sejajar silinder koaksial Susunan Kapasitor

Kapasitansi Kapasitor plat sejajar, silinder koaksial Susunan Kapasitor Energi yang Tersimpan dalam Kapasitor Dielektrik

Kapasitansi Sebuah kapasitor pada dasarnya terdiri dari dua buah plat konduktor sejajar dengan udara atau bahan isolator diantara keduanya. Sebuah kapasitor tidak harus kelihatan seperti plat logam. E V 0 L V 1 Kapasitor untuk penggunaan pada audio system dengan kualitas bagus.

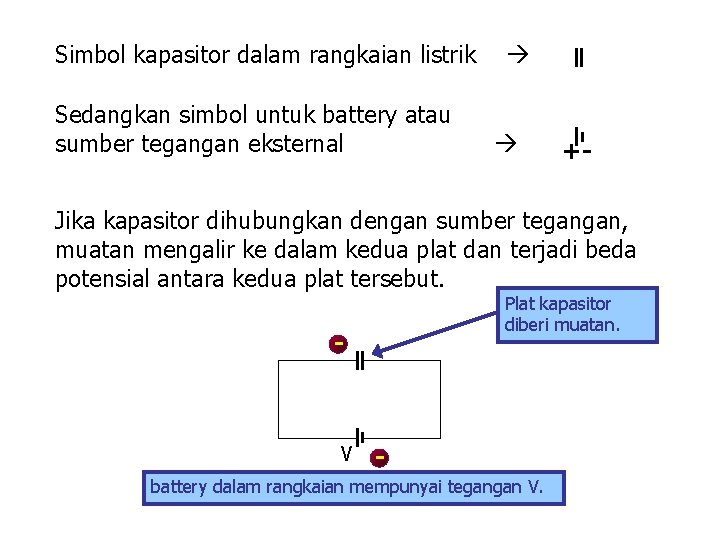
Simbol kapasitor dalam rangkaian listrik Sedangkan simbol untuk battery atau sumber tegangan eksternal +- Jika kapasitor dihubungkan dengan sumber tegangan, muatan mengalir ke dalam kedua plat dan terjadi beda potensial antara kedua plat tersebut. Plat kapasitor diberi muatan. - V - battery dalam rangkaian mempunyai tegangan V.

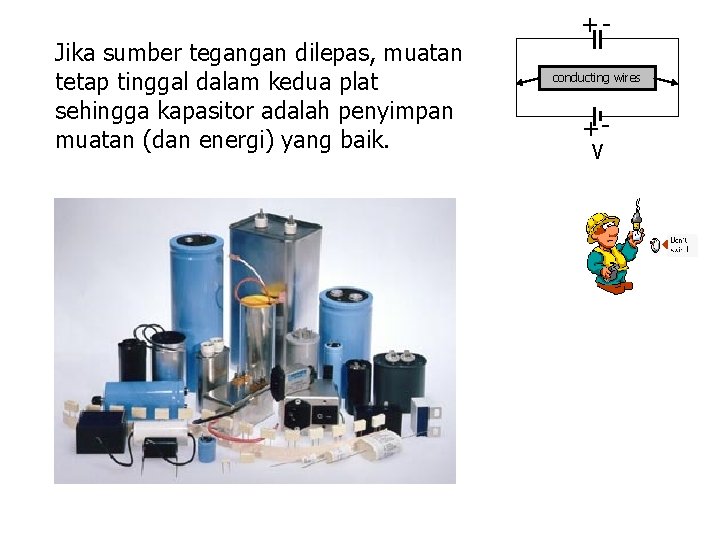
Jika sumber tegangan dilepas, muatan tetap tinggal dalam kedua plat sehingga kapasitor adalah penyimpan muatan (dan energi) yang baik. +conducting wires +V

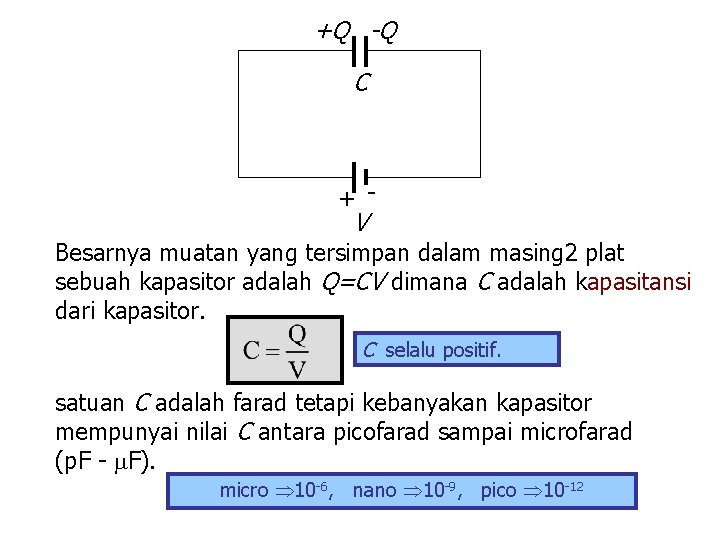
+Q -Q C + - V Besarnya muatan yang tersimpan dalam masing 2 plat sebuah kapasitor adalah Q=CV dimana C adalah kapasitansi dari kapasitor. C selalu positif. satuan C adalah farad tetapi kebanyakan kapasitor mempunyai nilai C antara picofarad sampai microfarad (p. F - F). micro 10 -6, nano 10 -9, pico 10 -12

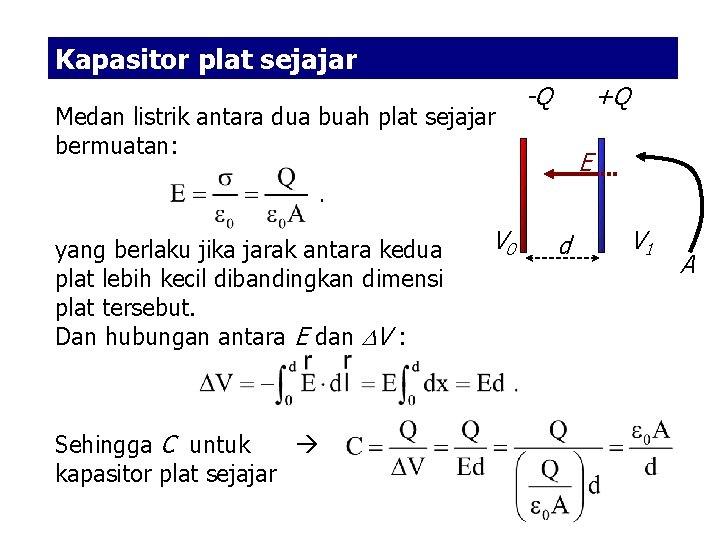
Kapasitor plat sejajar Medan listrik antara dua buah plat sejajar bermuatan: yang berlaku jika jarak antara kedua plat lebih kecil dibandingkan dimensi plat tersebut. Dan hubungan antara E dan V : Sehingga C untuk kapasitor plat sejajar V 0 -Q +Q E d V 1 A

Ingat: Q besarnya muatan pada masing 2 plat. V besarnya beda potensial antara kedua plat. V | V| atau biasanya dituliskan Vab. C selalu positif.

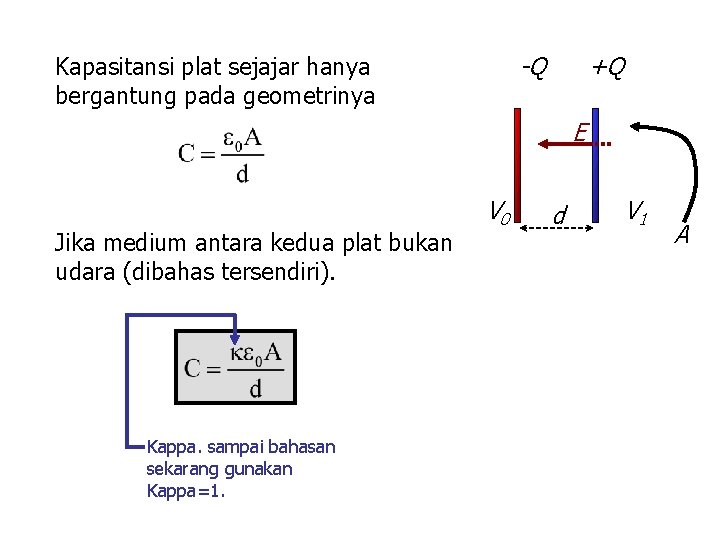
-Q Kapasitansi plat sejajar hanya bergantung pada geometrinya +Q E Jika medium antara kedua plat bukan udara (dibahas tersendiri). Kappa. sampai bahasan sekarang gunakan Kappa=1. V 0 d V 1 A

Kapasitor silinder koaksial Kita juga dapat menghitung kapasitansi kapasitor silinder koaksial (terbuat dari silinder koaksial). Bagaimana tampang lintang silinder di samping ini ? L

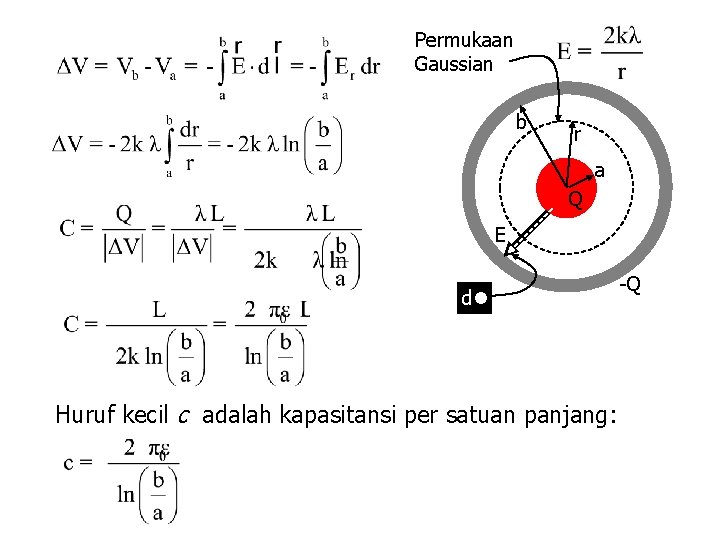
Permukaan Gaussian b r a Q E dl Huruf kecil c adalah kapasitansi per satuan panjang: -Q

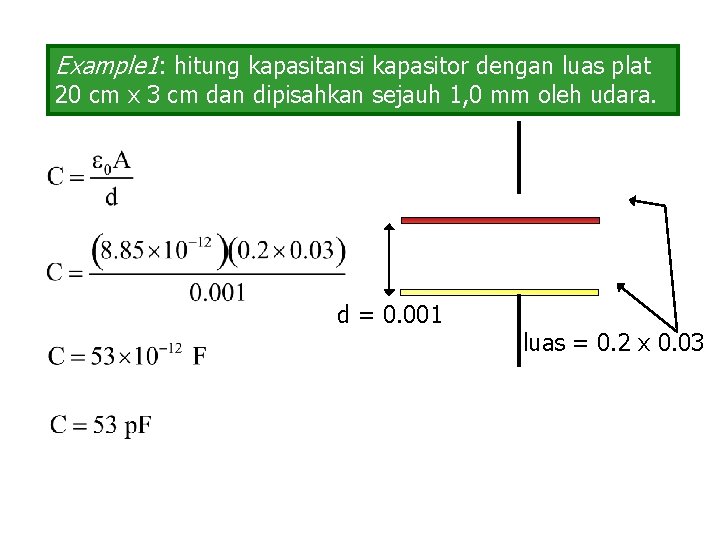
Example 1: hitung kapasitansi kapasitor dengan luas plat 20 cm x 3 cm dan dipisahkan sejauh 1, 0 mm oleh udara. d = 0. 001 luas = 0. 2 x 0. 03

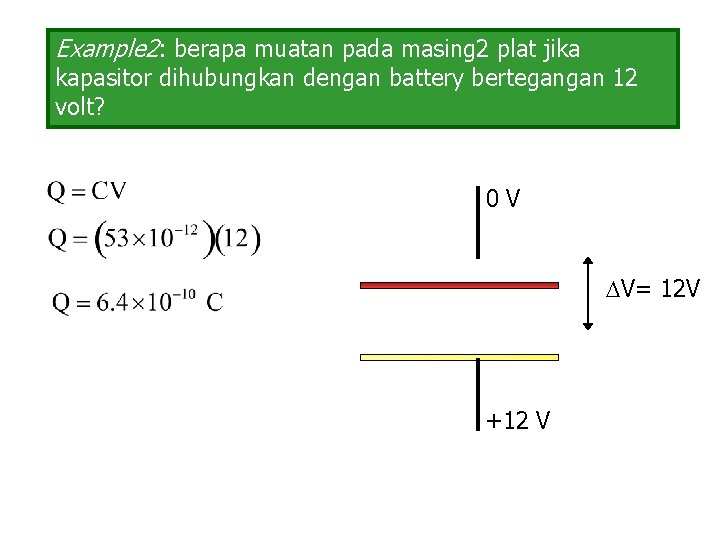
Example 2: berapa muatan pada masing 2 plat jika kapasitor dihubungkan dengan battery bertegangan 12 volt? 0 V V= 12 V +12 V

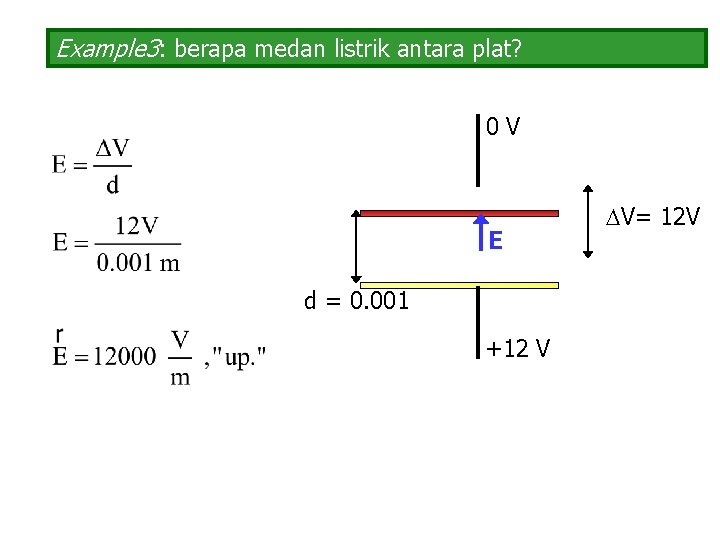
Example 3: berapa medan listrik antara plat? 0 V E d = 0. 001 +12 V V= 12 V

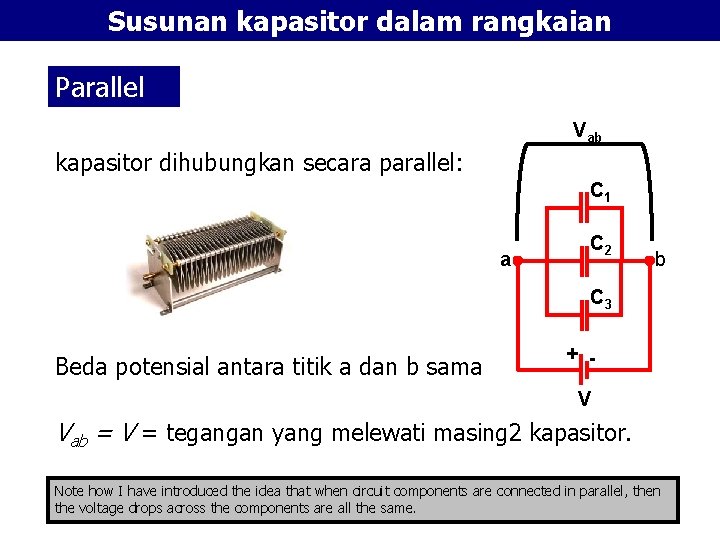
Susunan kapasitor dalam rangkaian Parallel Vab kapasitor dihubungkan secara parallel: C 1 a C 2 b C 3 + Beda potensial antara titik a dan b sama yaitu V. V Vab = V = tegangan yang melewati masing 2 kapasitor. Note how I have introduced the idea that when circuit components are connected in parallel, then the voltage drops across the components are all the same.

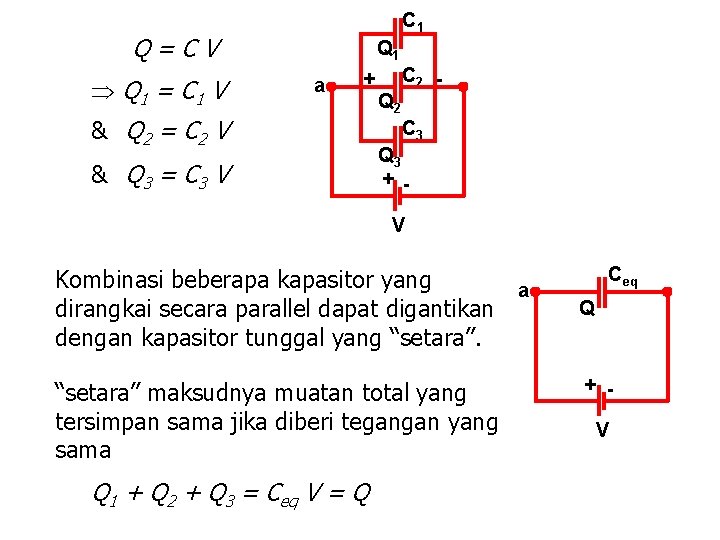
C 1 Q=CV Q 1 = C 1 V Q 1 a + & Q 2 = C 2 V & Q 3 = C 3 V Q 2 C 3 Q 3 + V Kombinasi beberapa kapasitor yang a dirangkai secara parallel dapat digantikan dengan kapasitor tunggal yang “setara” maksudnya muatan total yang tersimpan sama jika diberi tegangan yang sama Q 1 + Q 2 + Q 3 = Ceq V = Q Ceq Q + V

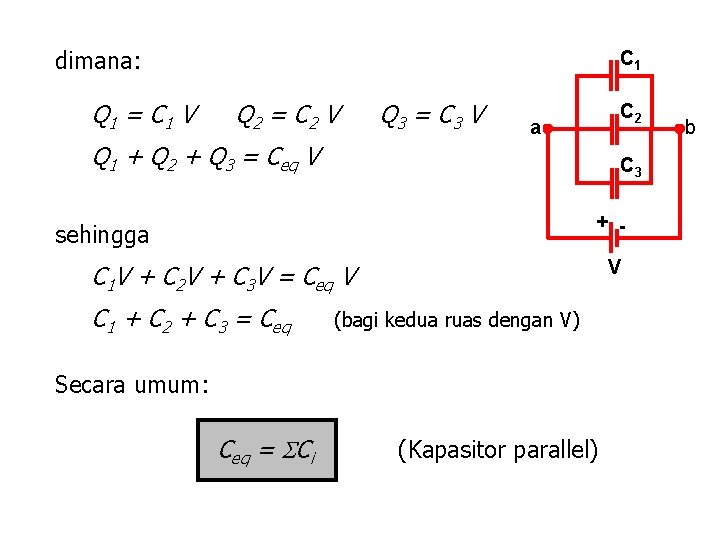
dimana: Q 1 = C 1 V C 1 Q 2 = C 2 V Q 3 = C 3 V C 2 a Q 1 + Q 2 + Q 3 = Ceq V C 3 + - sehingga V C 1 V + C 2 V + C 3 V = Ceq V C 1 + C 2 + C 3 = Ceq (bagi kedua ruas dengan V) Secara umum: Ceq = Ci (Kapasitor parallel) b

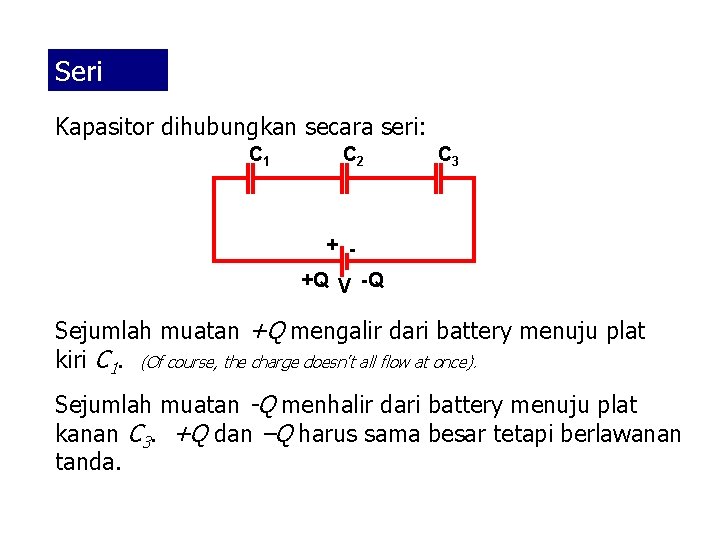
Seri Kapasitor dihubungkan secara seri: C 1 C 2 C 3 + +Q V -Q Sejumlah muatan +Q mengalir dari battery menuju plat kiri C 1. (Of course, the charge doesn’t all flow at once). Sejumlah muatan -Q menhalir dari battery menuju plat kanan C 3. +Q dan –Q harus sama besar tetapi berlawanan tanda.

muatan +Q and –Q menarik muatan yang sama dan berlawanan pada plat lainnya dari masing 2 kapasitor C 1 +Q -Q A C 2 +Q -Q B C 3 +Q -Q + V Muatan yang sama dan berlawanan ini berasal dari rangkaian netral pada daerag A dan B. Karena daerah A harus netral, harus ada muatan +Q pada plat kiri C 2. Karena daerah B juga harus netral, harus adal muatan -Q pada plat kanan C 2.

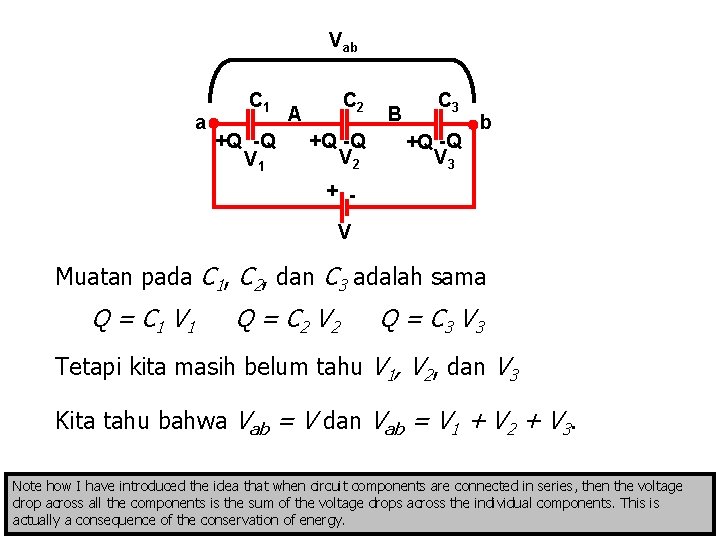
Vab a C 1 +Q -Q V 1 C 2 A +Q -Q V 2 B C 3 +Q -Q V 3 b + V Muatan pada C 1, C 2, dan C 3 adalah sama Q = C 1 V 1 Q = C 2 V 2 Q = C 3 V 3 Tetapi kita masih belum tahu V 1, V 2, dan V 3 Kita tahu bahwa Vab = V dan Vab = V 1 + V 2 + V 3. Note how I have introduced the idea that when circuit components are connected in series, then the voltage drop across all the components is the sum of the voltage drops across the individual components. This is actually a consequence of the conservation of energy.

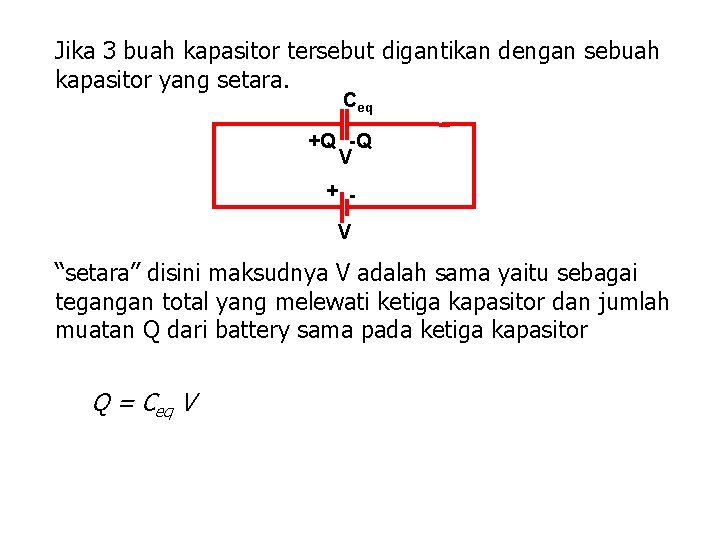
Jika 3 buah kapasitor tersebut digantikan dengan sebuah kapasitor yang setara. Ceq +Q -Q V + V “setara” disini maksudnya V adalah sama yaitu sebagai tegangan total yang melewati ketiga kapasitor dan jumlah muatan Q dari battery sama pada ketiga kapasitor Q = Ceq V

dimana: Q = C 1 V 1 Q = C 2 V 2 Q = C 3 Vab = V 1 + V 2 + V 3. Q = Ceq V Substitusi untuk V 1, V 2, dan V 3: Substitusi untuk V: Bagi kedua ruas dengan Q:

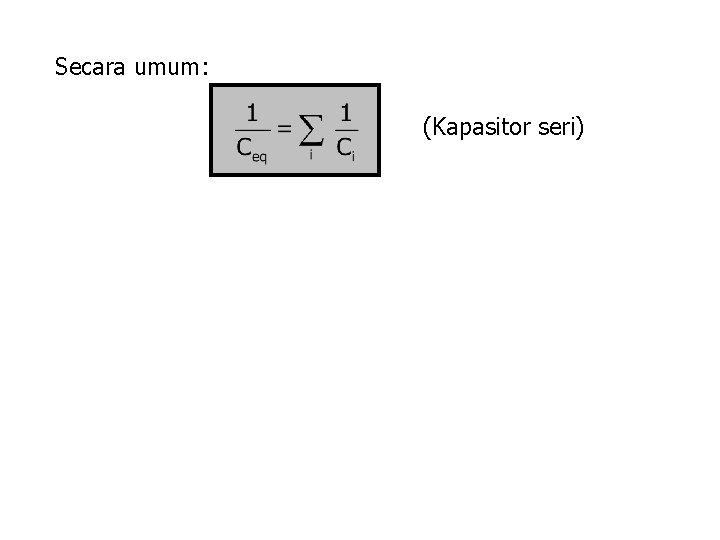
Secara umum: (Kapasitor seri)

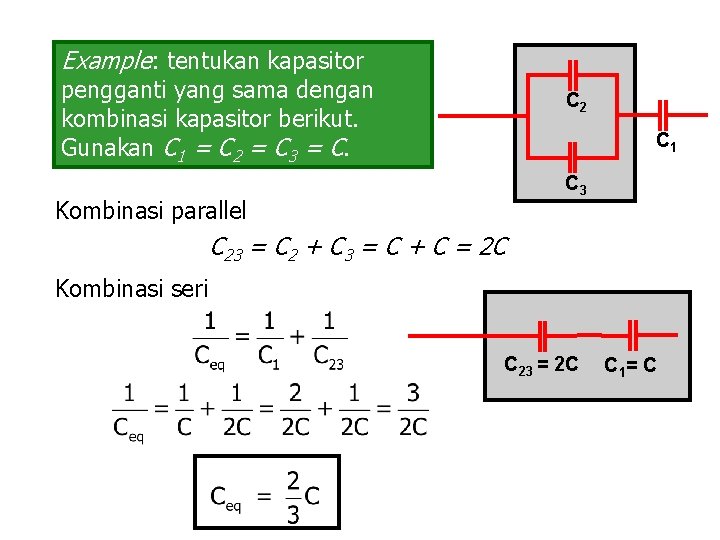
Example: tentukan kapasitor pengganti yang sama dengan kombinasi kapasitor berikut. Gunakan C 1 = C 2 = C 3 = C. C 2 C 1 C 3 Kombinasi parallel C 23 = C 2 + C 3 = C + C = 2 C Kombinasi seri C 23 = 2 C C 1 = C

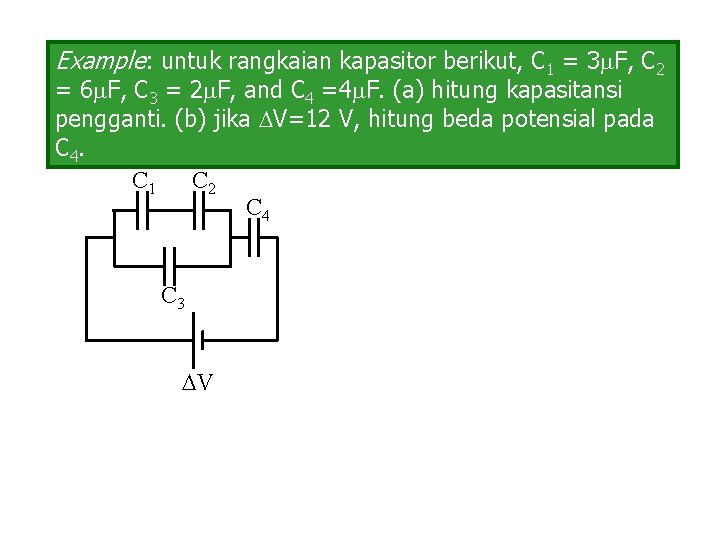
Example: untuk rangkaian kapasitor berikut, C 1 = 3 F, C 2 = 6 F, C 3 = 2 F, and C 4 =4 F. (a) hitung kapasitansi pengganti. (b) jika V=12 V, hitung beda potensial pada C 4. C 1 C 2 C 4 C 3 V

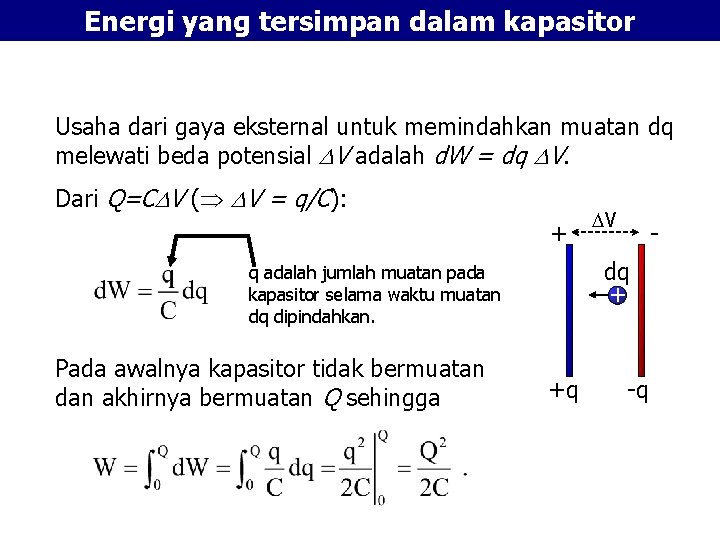
Energi yang tersimpan dalam kapasitor Usaha dari gaya eksternal untuk memindahkan muatan dq melewati beda potensial V adalah d. W = dq V. Dari Q=C V ( V = q/C): + - dq + q adalah jumlah muatan pada kapasitor selama waktu muatan dq dipindahkan. Pada awalnya kapasitor tidak bermuatan dan akhirnya bermuatan Q sehingga V +q -q

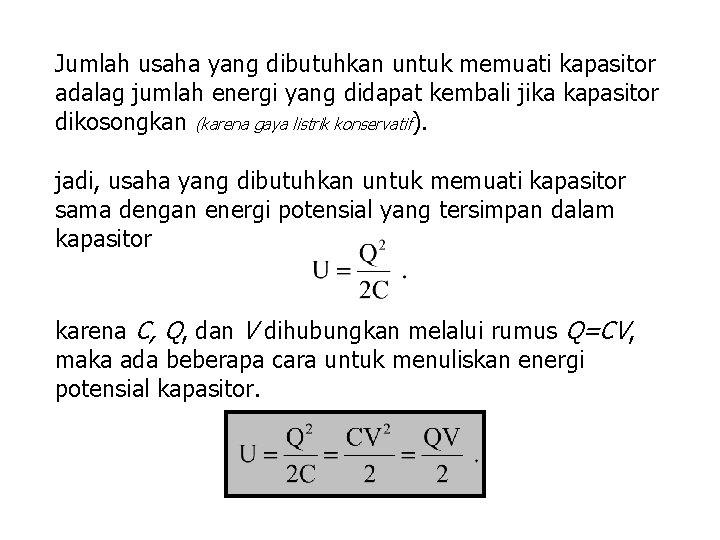
Jumlah usaha yang dibutuhkan untuk memuati kapasitor adalag jumlah energi yang didapat kembali jika kapasitor dikosongkan (karena gaya listrik konservatif). jadi, usaha yang dibutuhkan untuk memuati kapasitor sama dengan energi potensial yang tersimpan dalam kapasitor karena C, Q, dan V dihubungkan melalui rumus Q=CV, maka ada beberapa cara untuk menuliskan energi potensial kapasitor.

Example: flash kamera menyimpan energi dalam sebuah kapasitor 150 F pada 200 V. Berapa banyak energi listrik yang dapat tersimpan?

Energi tersimpan dalam kapasitor: V + - E +Q “volume kapasitor” =Ad Energi tersimpan per satuan volume (u): energi tersimpan dalam bentuk medan listrik d -Q area A

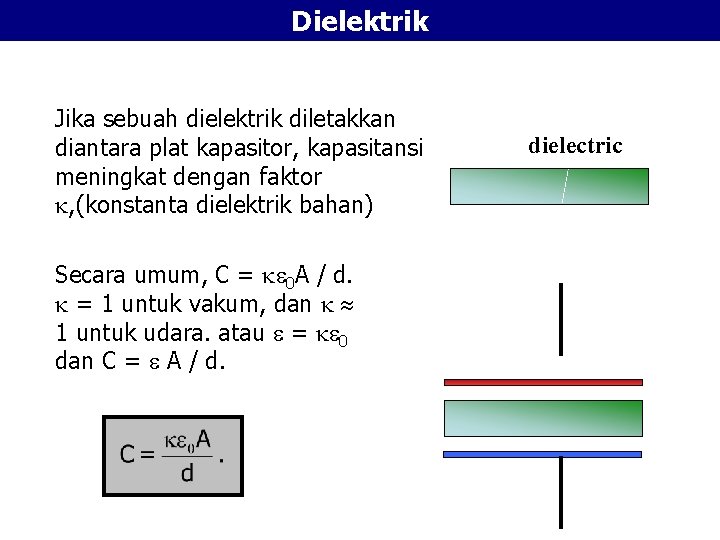
Dielektrik Jika sebuah dielektrik diletakkan diantara plat kapasitor, kapasitansi meningkat dengan faktor , (konstanta dielektrik bahan) Secara umum, C = 0 A / d. = 1 untuk vakum, dan 1 untuk udara. atau = 0 dan C = A / d. dielectric

dielektrik adalah isolator tipis yang diletakkan diantara plat kapasitor. dielectric alasan penggunaan kapasitor? Mendapatkan kapasitor dengan C yang besar untuk geometri tertentu ( >1)

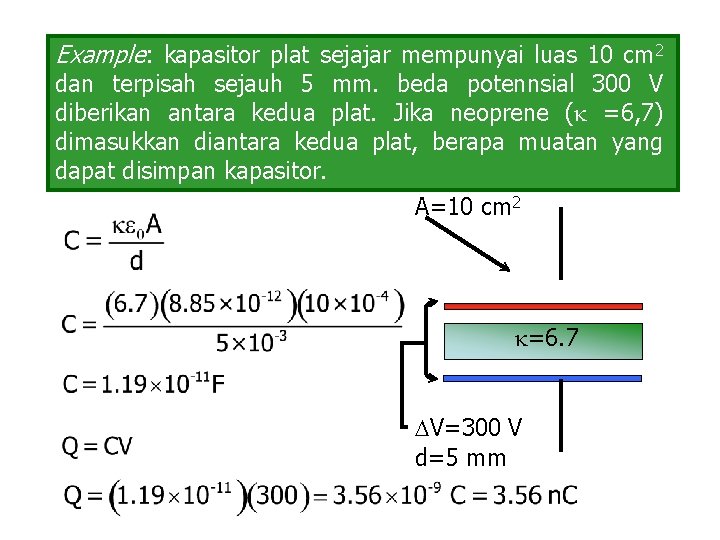
Example: kapasitor plat sejajar mempunyai luas 10 cm 2 dan terpisah sejauh 5 mm. beda potennsial 300 V diberikan antara kedua plat. Jika neoprene ( =6, 7) dimasukkan diantara kedua plat, berapa muatan yang dapat disimpan kapasitor. A=10 cm 2 =6. 7 V=300 V d=5 mm

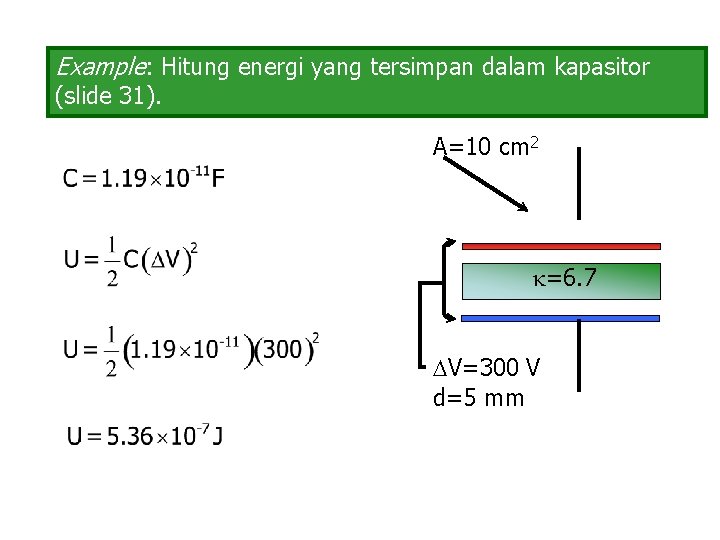
Example: Hitung energi yang tersimpan dalam kapasitor (slide 31). A=10 cm 2 =6. 7 V=300 V d=5 mm

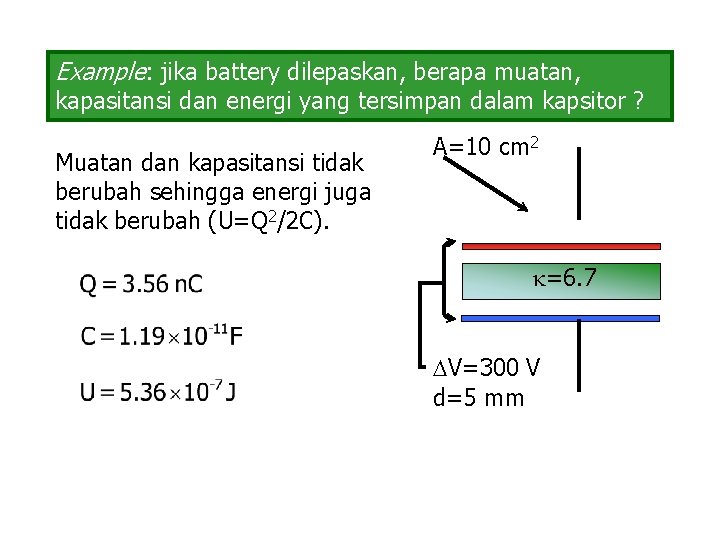
Example: jika battery dilepaskan, berapa muatan, kapasitansi dan energi yang tersimpan dalam kapsitor ? Muatan dan kapasitansi tidak berubah sehingga energi juga tidak berubah (U=Q 2/2 C). A=10 cm 2 =6. 7 V=300 V d=5 mm

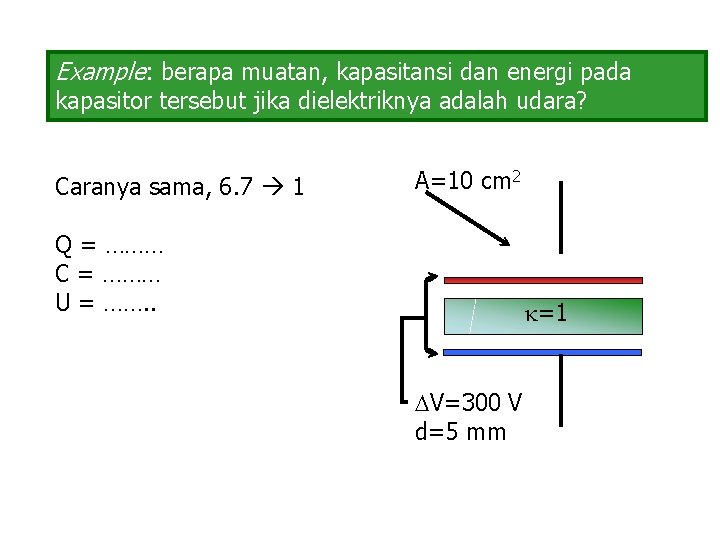
Example: berapa muatan, kapasitansi dan energi pada kapasitor tersebut jika dielektriknya adalah udara? Caranya sama, 6. 7 1 A=10 cm 2 Q = ……… C = ……… U = ……. . =1 V=300 V d=5 mm