Kap 09 Tre Slektstre med ulike generasjoner foreldre





















![Heap Building a max binary heap - Algorithm Gitt en array a[1. . n] Heap Building a max binary heap - Algorithm Gitt en array a[1. . n]](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-44.jpg)
![Heap. Sort - Algorithm [1/2] 4 8 3 2 7 5 Heap. Sort_Max. Bin. Heap. Sort - Algorithm [1/2] 4 8 3 2 7 5 Heap. Sort_Max. Bin.](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-46.jpg)
![8 Heap 8 7 5 2 4 3 Heap. Sort - Algorithm [2/2] 3 8 Heap 8 7 5 2 4 3 Heap. Sort - Algorithm [2/2] 3](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-47.jpg)





















![Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [1/2] Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [1/2]](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-96.jpg)
![Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [2/2] l. Pek Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [2/2] l. Pek](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-97.jpg)





































- Slides: 156

Kap 09 Tre

Slektstre med ulike generasjoner (foreldre, barnebarn, …)

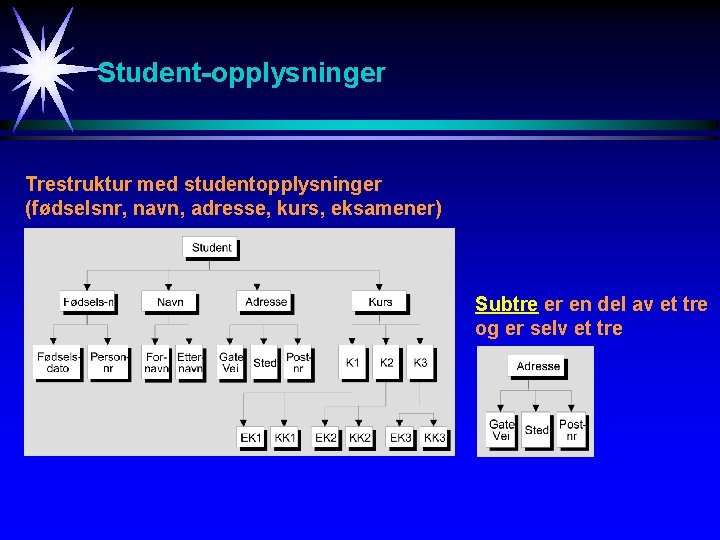
Student-opplysninger Trestruktur med studentopplysninger (fødselsnr, navn, adresse, kurs, eksamener) Subtre er en del av et tre og er selv et tre

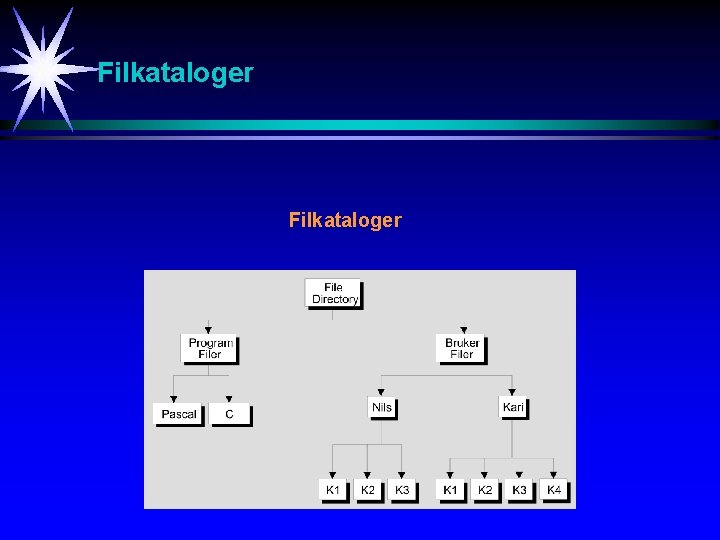
Filkataloger

Kompilering av program ved programsplitting i en trestruktur void main ( ) { int a, b; cout << ”Oppgi a: ”; cin >> a; cout << ”Oppgi b: ”; cin >> b; if(a>b) cout << ”Største tall: ” << a; else cout << ”Største tall: ” << b; }

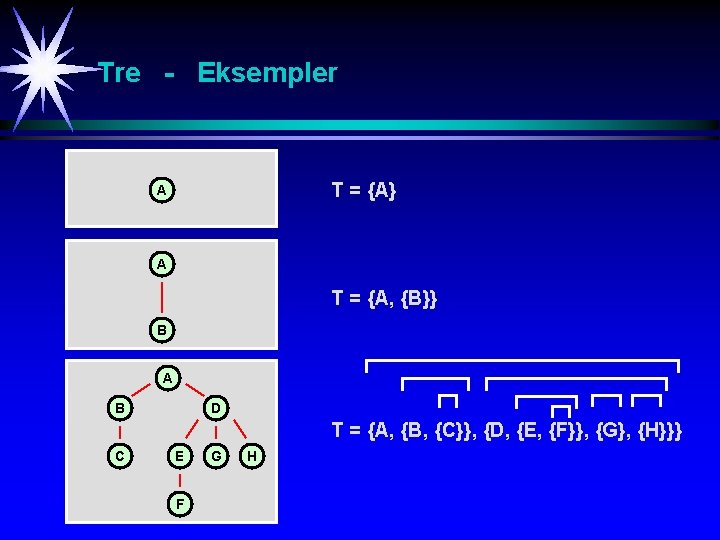
Tre - Definisjon Et tre T er en endelig mengde av noder med følgende egenskaper: 1. Enten er mengden tom, T = Ø, eller 2. Mengden består av en node R kalt rot og de resterende nodene er partisjonert i n >= 0 såkalte subtrær T 1, T 2, …, Tn hvor hver Ti selv er et tre. T = {R} U T 1 U T 2 U … U Tn = {R, T 1, T 2, …, Tn}

Tre - Eksempler T = {A} A A T = {A, {B}} B A B D T = {A, {B, {C}}, {D, {E, {F}}, {G}, {H}}} C E F G H

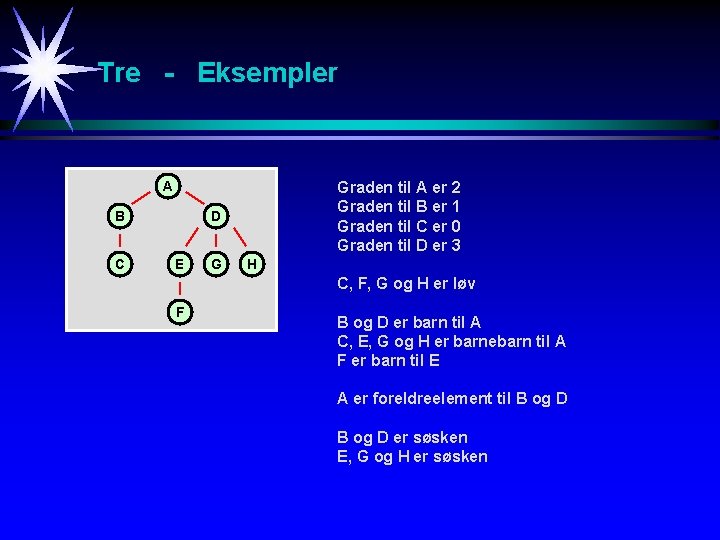
Tre - Definisjoner T = {R, T 1, T 2, …, Tn} Graden til en node er antall subtre assosiert med denne noden. Et løv er en node med grad null (har ingen subtre). Hver rot Ri i subtreet Ti til treet T kalles et barn til R. Tilsvarende defineres barnebarn, …. Roten R i treet T kalles foreldreelement til alle røttene Ri i subtreet Ti 1 < i <= n. Tilsvarende defineres besteforeldre. To røtter Ri og Rj av distinkte subtrær Ti og Tj i treet T kalles søsken.

Tre - Eksempler A B C Graden til A er 2 Graden til B er 1 Graden til C er 0 Graden til D er 3 D E G H C, F, G og H er løv F B og D er barn til A C, E, G og H er barnebarn til A F er barn til E A er foreldreelement til B og D er søsken E, G og H er søsken

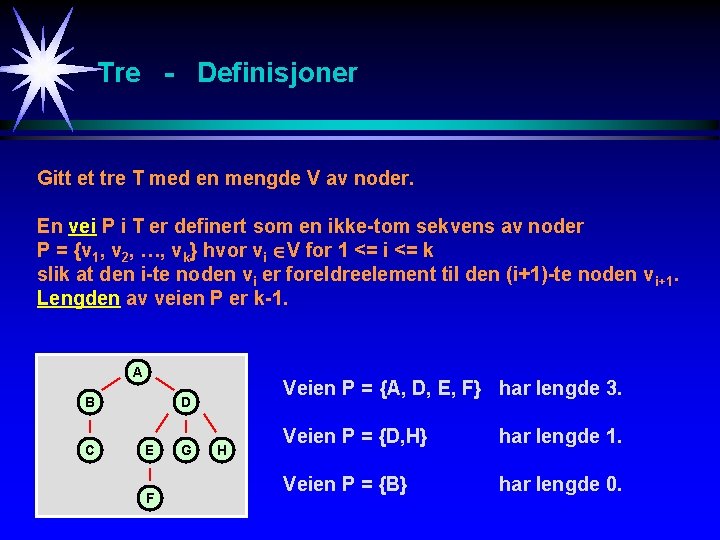
Tre - Definisjoner Gitt et tre T med en mengde V av noder. En vei P i T er definert som en ikke-tom sekvens av noder P = {v 1, v 2, …, vk} hvor vi V for 1 <= i <= k slik at den i-te noden vi er foreldreelement til den (i+1)-te noden vi+1. Lengden av veien P er k-1. A B C Veien P = {A, D, E, F} har lengde 3. D E F G H Veien P = {D, H} har lengde 1. Veien P = {B} har lengde 0.

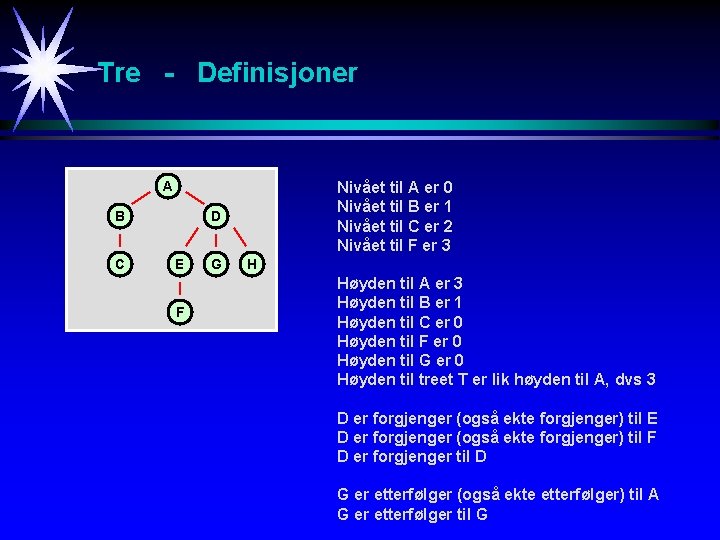
Tre - Definisjoner Gitt et tre T med en mengde V av noder. Nivået eller dybden til en node vi V i T er definert som lengden av den entydige veien i T fra roten R til noden v i. Høyden til en node vi V i T er definert som den lengste veien fra noden vi til et løv. Høyden til et tre T er definert som høyden til roten R. La vi og vj V. vi sies å være en forgjenger til vj hvis det finnes en vei fra vi til vj. vi og vj kan være samme node. vi sies å være en ekte forgjenger til vj hvis det finnes en vei med lengde ulik null fra vi til vj. Tilsvarende defineres etterfølger og ekte etterfølger.

Tre - Definisjoner A B C Nivået til A er 0 Nivået til B er 1 Nivået til C er 2 Nivået til F er 3 D E F G H Høyden til A er 3 Høyden til B er 1 Høyden til C er 0 Høyden til F er 0 Høyden til G er 0 Høyden til treet T er lik høyden til A, dvs 3 D er forgjenger (også ekte forgjenger) til E D er forgjenger (også ekte forgjenger) til F D er forgjenger til D G er etterfølger (også ekte etterfølger) til A G er etterfølger til G

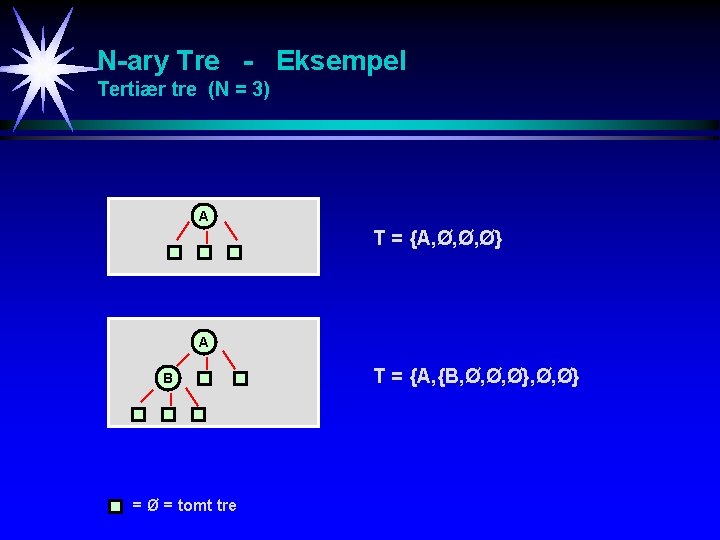
N-ary Tre - Definisjon Et N-ary tre T er et tre hvor alle nodene har samme grad N. T = {R, T 0, T 1, …, TN-1} hvor hver Ti er et N-ary tre Det tomme treet kalles en ekstern node fordi det ikke har noe subtre. Et ikke-tomt tre kalles en intern node. Et løv er en intern node som kun har eksterne subtrær.

N-ary Tre - Eksempel Tertiær tre (N = 3) A T = {A, Ø, Ø, Ø} A B = Ø = tomt tre T = {A, {B, Ø, Ø, Ø}

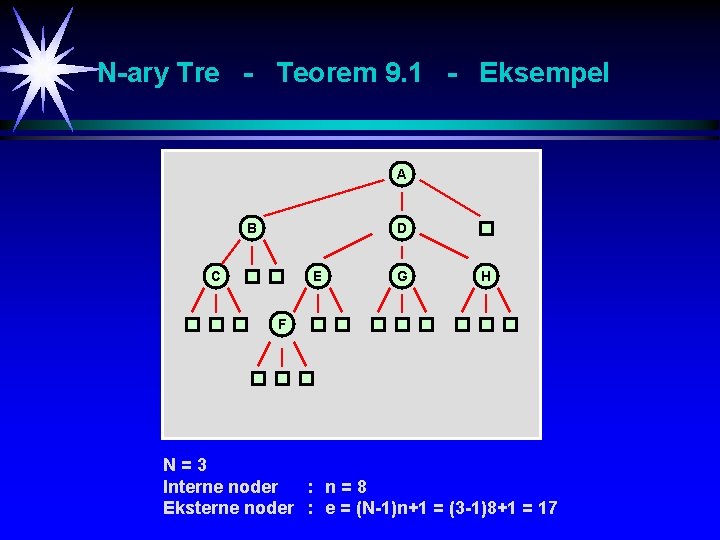
N-ary Tre - Teorem 9. 1: Et N-ary tre med n >= 0 noder inneholder (N-1)n+1 eksterne noder. Bevis: La antall eksterne noder være e. Siden hver node unntatt roten (tom eller ikke) har ett foreldreelement, må det være (n+e-1)/N foreldreelementer i treet siden hvert foreldreelement har N barn. Herav har vi: n = (n+e-1)/N som gir e = (N-1)n+1.

N-ary Tre - Teorem 9. 1 - Eksempel A B D C E G H F N=3 Interne noder : n=8 Eksterne noder : e = (N-1)n+1 = (3 -1)8+1 = 17

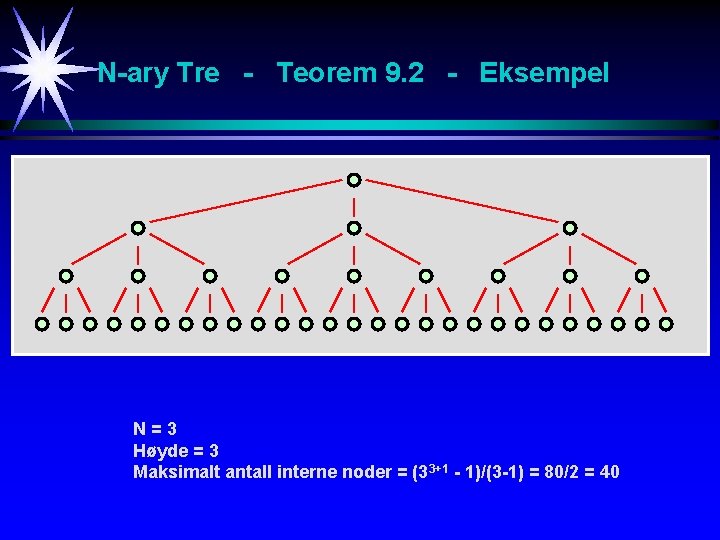
1 N-ary Tre - Teorem 9. 2: La T være et N-ary tre med høyde h >= 0. Maksimalt antall interne noder i T er da gitt ved: (Nh+1 -1)/(N-1) Bevis: (ved induksjon) La T være et N-ary tre med høyde null. Det består av en intern node og N tomme subtrær. Teoremet holder derfor h = 0 siden (N 0+1 -1)/(N-1) = (N-1)/(N-1) = 1. Anta at teoremet holder for h = 0, 1, 2, …, k hvor k >= 0. La T være et N-ary tre med høyde k+1. Et slikt tre består av en rot og N subtrær hver inneholdene høyst (Nk+1 -1)/(N-1) interne noder. Maksimalt antall interne noder er derfor: N(Nk+1 -1)/(N-1)+1 = (Nk+2 -1)/(N-1) k k+1 … …

N-ary Tre - Teorem 9. 2 - Eksempel N=3 Høyde = 3 Maksimalt antall interne noder = (33+1 - 1)/(3 -1) = 80/2 = 40

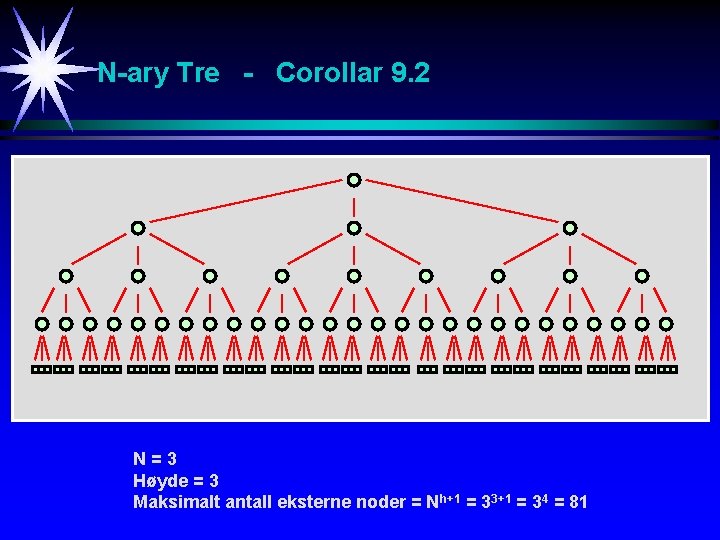
N-ary Tre - Corollar 9. 2: La T være et N-ary tre med høyde h >= 0. Maksimalt antall eksterne noder i T er da gitt ved: (N-1)(Nh+1 -1)/(N-1) + 1 = Nh+1 nmax Hint (fra teorem 9. 1): emax = (N-1)nmax + 1

N-ary Tre - Corollar 9. 2 N=3 Høyde = 3 Maksimalt antall eksterne noder = Nh+1 = 33+1 = 34 = 81

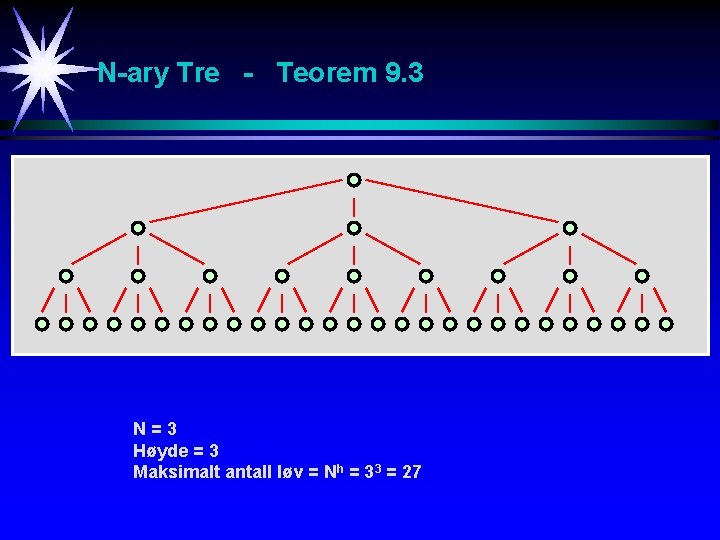
1 N-ary Tre - Teorem 9. 3: La T være et N-ary tre med høyde h >= 0. Maksimalt antall løv noder i T er da gitt ved: Nh Bevis: (ved induksjon) La T ha høyde null. T består av nøyaktig en node som har N tomme subtrær. Den ene noden er derfor et løv. Teoremet holder for h = 0 siden N 0 = 1. Anta at teoremet holder for h = 0, 1, 2, …, k. La T ha høyde k+1. Foruten en rot R består T av N subtrær som hver har høyest Nk løv. Maksimalt antall løv er derfor N x Nk = Nk+1 k k+1 … …

N-ary Tre - Teorem 9. 3 N=3 Høyde = 3 Maksimalt antall løv = Nh = 33 = 27

Binært tre - Definisjon Et binært tre er et N-ary tre hvor N = 2, dvs hver node har eksakt to barn (uten eksterne noder maksimalt to barn). T = {R, TL, TR} TL og TR kalles for henholdsvis venstre subtre og høyre subtre. A A B C D B = C D

Tre gjennomløping A B Tre gjennomløping: C - Bredde først gjennomløp - Dybde først gjennomløp - Pre. Orden gjennomløp - In. Orden gjennomløp (kun for binært tre) - Post. Orden gjennomløp D E F H

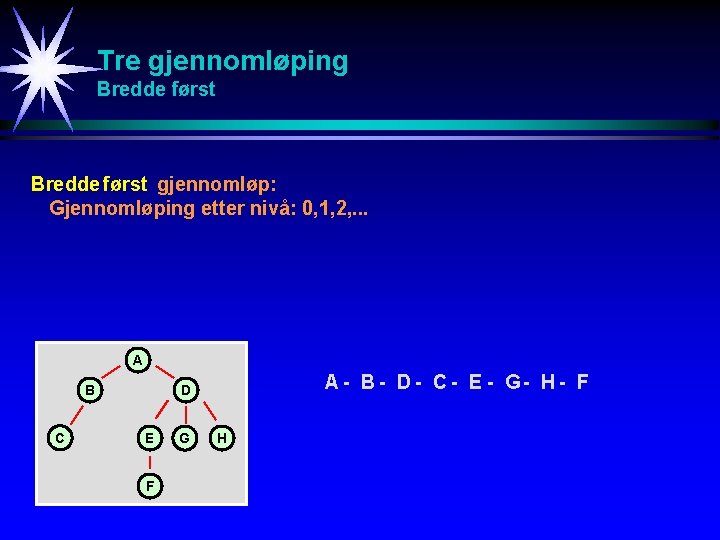
Tre gjennomløping Bredde først gjennomløp: Gjennomløping etter nivå: 0, 1, 2, . . . A B C A - B - D - C - E - G- H - F D E F G H

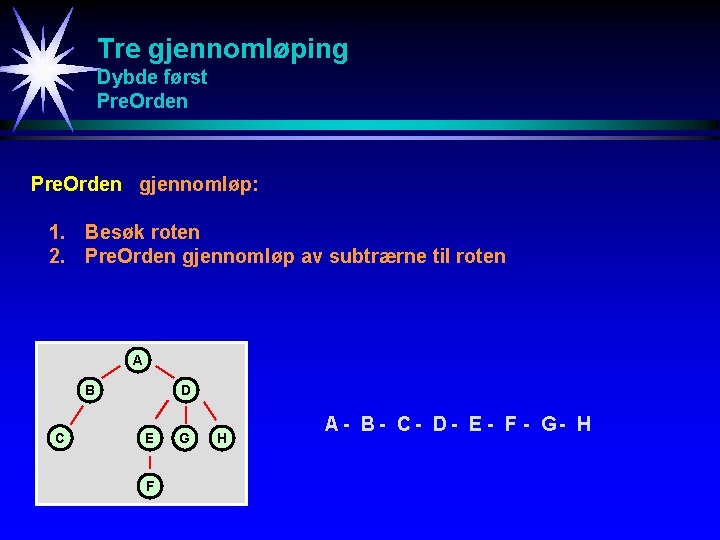
Tre gjennomløping Dybde først Pre. Orden gjennomløp: 1. Besøk roten 2. Pre. Orden gjennomløp av subtrærne til roten A B C D E F G H A - B - C - D - E - F - G- H

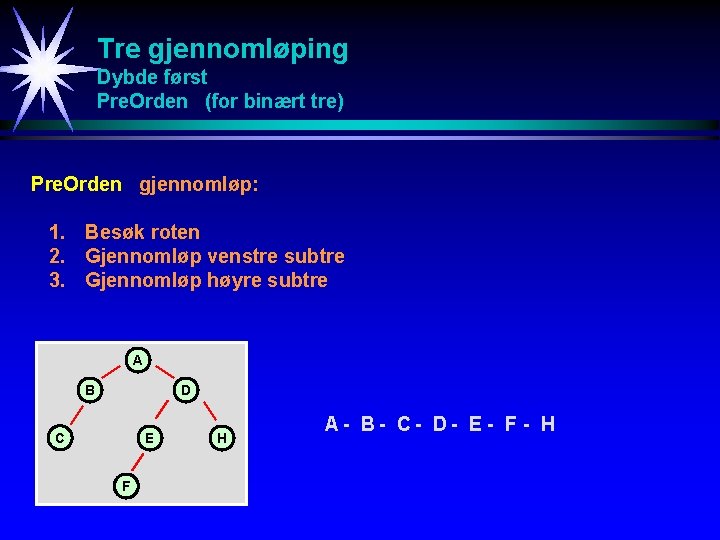
Tre gjennomløping Dybde først Pre. Orden (for binært tre) Pre. Orden gjennomløp: 1. Besøk roten 2. Gjennomløp venstre subtre 3. Gjennomløp høyre subtre A B D C E F H A- B- C- D- E - F - H

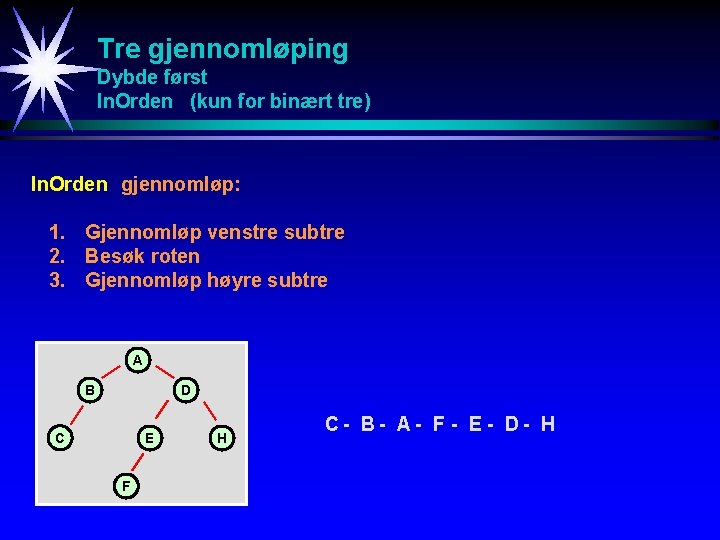
Tre gjennomløping Dybde først In. Orden (kun for binært tre) In. Orden gjennomløp: 1. Gjennomløp venstre subtre 2. Besøk roten 3. Gjennomløp høyre subtre A B D C E F H C- B- A- F - E - D- H

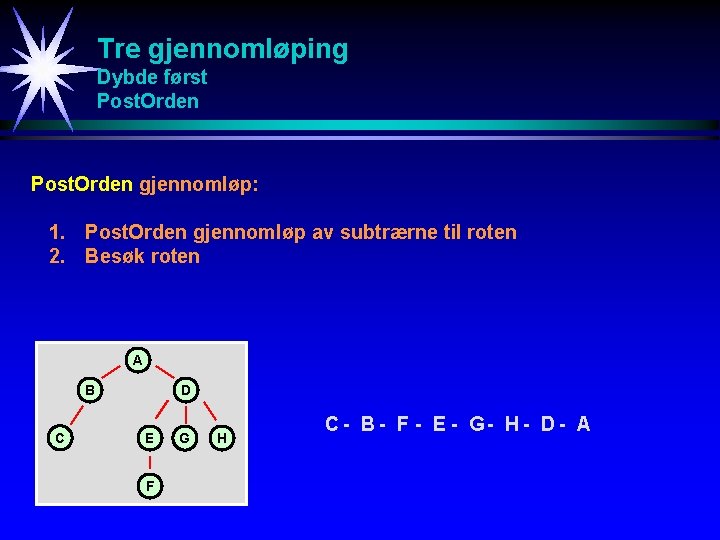
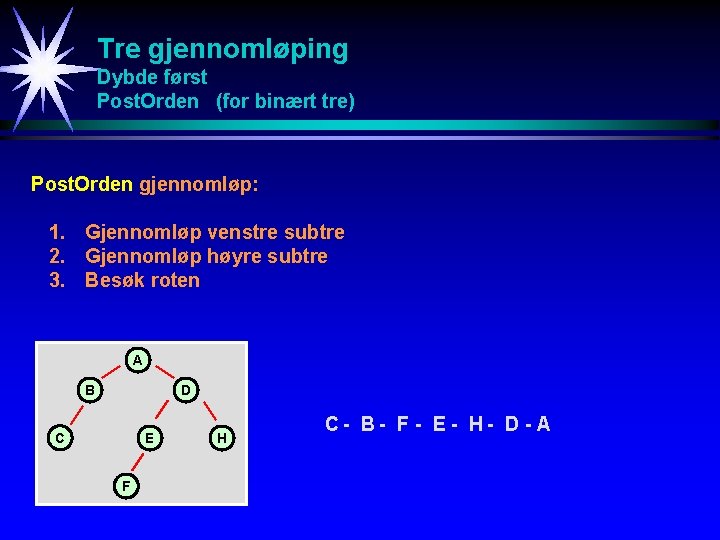
Tre gjennomløping Dybde først Post. Orden gjennomløp: 1. Post. Orden gjennomløp av subtrærne til roten 2. Besøk roten A B C D E F G H C - B - F - E - G- H - D - A

Tre gjennomløping Dybde først Post. Orden (for binært tre) Post. Orden gjennomløp: 1. Gjennomløp venstre subtre 2. Gjennomløp høyre subtre 3. Besøk roten A B D C E F H C- B- F - E - H- D - A

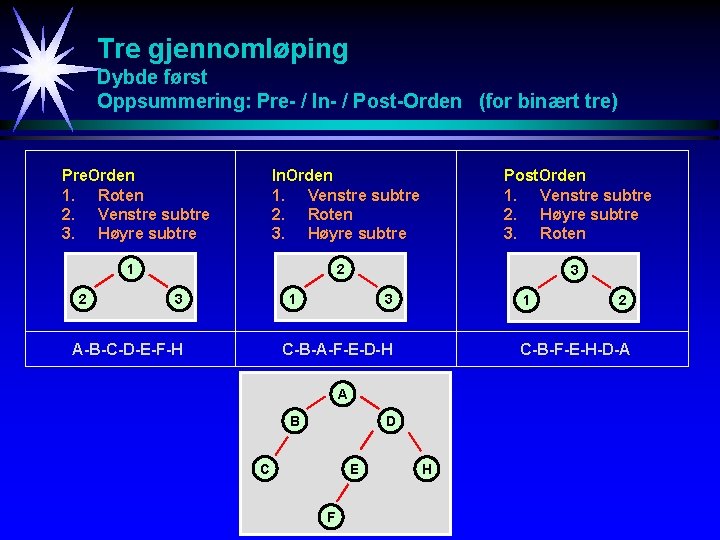
Tre gjennomløping Dybde først Oppsummering: Pre- / In- / Post-Orden (for binært tre) Pre. Orden 1. Roten 2. Venstre subtre 3. Høyre subtre In. Orden 1. Venstre subtre 2. Roten 3. Høyre subtre 1 2 Post. Orden 1. Venstre subtre 2. Høyre subtre 3. Roten 2 3 3 1 A-B-C-D-E-F-H 3 1 C-B-A-F-E-D-H C-B-F-E-H-D-A A B D C E F 2 H

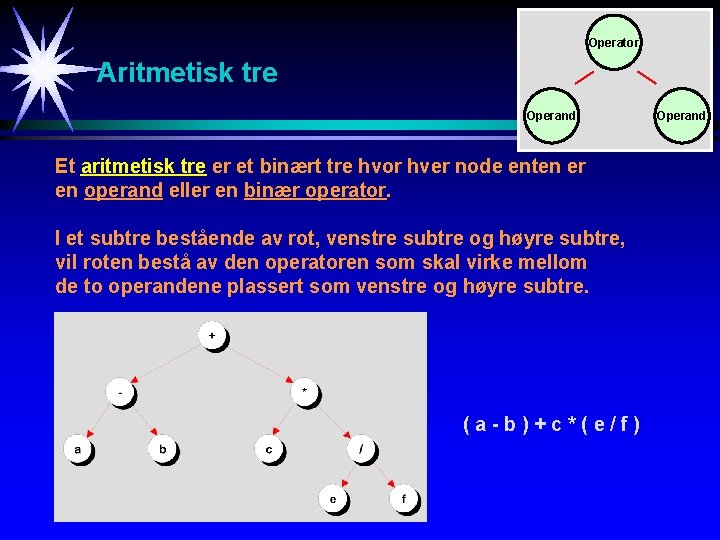
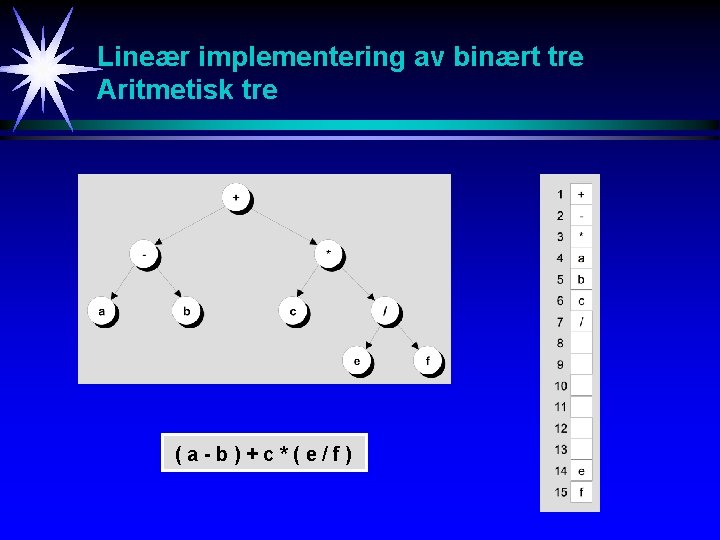
Operator Aritmetisk tre Operand Et aritmetisk tre er et binært tre hvor hver node enten er en operand eller en binær operator. I et subtre bestående av rot, venstre subtre og høyre subtre, vil roten bestå av den operatoren som skal virke mellom de to operandene plassert som venstre og høyre subtre. (a-b)+c*(e/f) Operand

Traversering av et binært tre Aritmetisk tre Preorder traversal : +-ab*c/ef 1. Besøk roten 2. Gjennomløp venstre subtre 3. Gjennomløp høyre subtre Inorder traversal : (a-b)+c*(e/f) 1. Gjennomløp venstre subtre 2. Besøk roten 3. Gjennomløp høyre subtre Postorder traversal : 1. Gjennomløp venstre subtre 2. Gjennomløp høyre subtre 3. Besøk roten ab-cef/*+

Aritmetisk tre In. Orden gjennomløp 1. 2. 3. 4. 5. Skriv venstreparentes Gjennomløp venstre subtre Skriv roten Gjennomløp høyre subtre Skriv høyre parentes (( a - b ) + (c * ( e / f ))) (a-b)+c*(e/f)

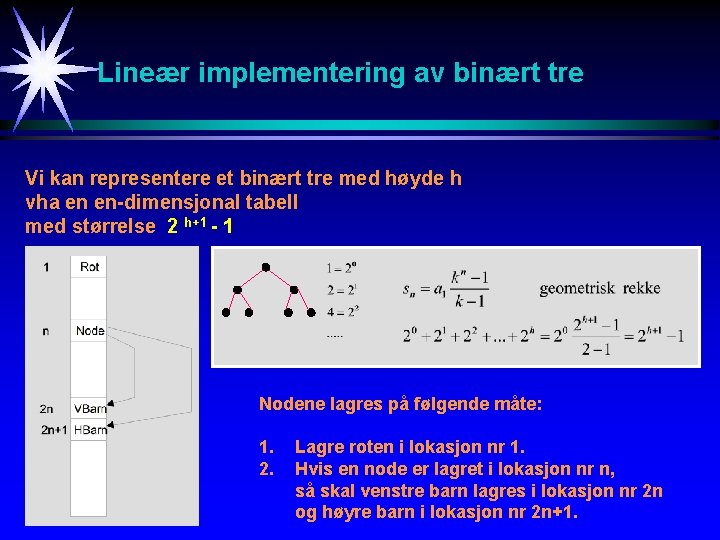
Lineær implementering av binært tre Vi kan representere et binært tre med høyde h vha en en-dimensjonal tabell med størrelse 2 h+1 - 1 Nodene lagres på følgende måte: 1. 2. Lagre roten i lokasjon nr 1. Hvis en node er lagret i lokasjon nr n, så skal venstre barn lagres i lokasjon nr 2 n og høyre barn i lokasjon nr 2 n+1.

Lineær implementering av binært tre Aritmetisk tre (a-b)+c*(e/f)

Lineær implementering av binært tre Aritmetisk tre (a-b)+c*(e/f) Fordeler: - Enkel sammenheng mellom far/barn. Far i lokasjon n => barn i lokasjon 2 n og 2 n+1. Et barn i lokasjon n => far i lokasjon n DIV 2. - Kan lett implementeres i alle språk. Ulemper: - Kan medføre plass-sløsing. - Kan medføre mye flytting ved. innsetting/sletting.

Heap er hensiktsmessig bl. a. ved sortering, prioritetskø og komprimering En heap er en trestruktur med følgende undergrupper: Max. Heap Generelt tre hvor hver node har nøkkelverdi større enn eller lik nøkkelverdi til hvert av sine barn Max. Bin. Heap Binært tre hvor hver node har nøkkelverdi større enn eller lik nøkkelverdi til hvert av sine barn Min. Heap Generelt tre hvor hver node har nøkkelverdi mindre enn eller lik nøkkelverdi til hvert av sine barn Min. Bin. Heap Binært tre hvor hver node har nøkkelvedi mindre enn eller lik nøkkelverdi til hvert av sine barn 8 5 3 7 2 6 4 1 8 5 3 7 2 6 1 2 5 6 3 8 4 9 7 2 5 7 3 9 4 8

Heap Binary Heap Benytter lineær implementering med innsetting fra venstre, nivå for nivå Max. Bin. Heap Binært tre hvor hver node har nøkkelverdi større enn eller lik nøkkelverdi til hvert av sine barn Min. Bin. Heap Binært tre hvor hver node har nøkkelvedi mindre enn eller lik nøkkelverdi til hvert av sine barn

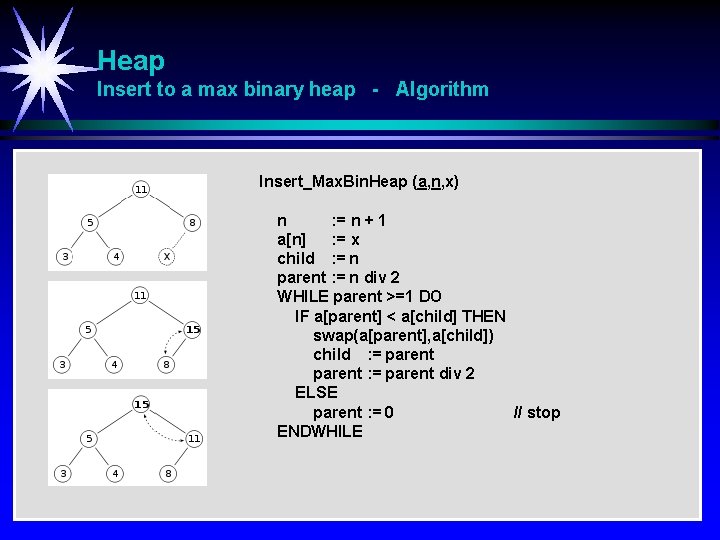
Heap Insert to a max binary heap 1. Adder nytt element til bunnen av heap’en. 2. Sammenlign nytt element med foreldre-element. Hvis korrekt rekkefølge, stopp. 3. Hvis ikke korrekt rekkefølge, bytt nytt element med foreldre-element og fortsett i pkt 2.

Heap Insert to a max binary heap - Algorithm Insert_Max. Bin. Heap (a, n, x) n : = n + 1 a[n] : = x child : = n parent : = n div 2 WHILE parent >=1 DO IF a[parent] < a[child] THEN swap(a[parent], a[child]) child : = parent div 2 ELSE parent : = 0 // stop ENDWHILE

Heap Delete from a max binary heap 1. Kopier roten i heap’en. 2. Erstatt roten med siste element i siste nivå. Hvis korrekt rekkefølge, stopp. 3. Hvis ikke korrekt rekkefølge, gjennomfør ’buble-down’ (swap med det største barnet), inntil heap-egenskapen er gjenopprettet.

Heap Delete from a max binary heap Delete_Max. Bin. Heap (a, n, top, empty) IF (n == 0) THEN empty : = true ELSE empty : = false top : = a[1] : = a[n] n : = n – 1 parent : = 1 child : = 2 WHILE (child <= n – 1) DO IF (a[child] < a[child+1]) THEN child : = child + 1 ENDIF IF (a[child] > a[parent]) THEN swap(a[parent], a[child]) parent : = child : = 2*child ELSE child : = n ENDIF ENDWHILE ENDIF // stop
![Heap Building a max binary heap Algorithm Gitt en array a1 n Heap Building a max binary heap - Algorithm Gitt en array a[1. . n]](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-44.jpg)
Heap Building a max binary heap - Algorithm Gitt en array a[1. . n] av elementer i vilkårlig rekkefølge. 4 8 3 2 7 5 Induksjon: 1. a[1] er en heap 2. Anta at a[1. . k] er en heap 3. Tilordning av a[1. . k+1] til en heap 8 4 3 2 Benytt Insert_Max. Bin. Heap til å innsette element nr k+1 i heap a[1. . k] Build_Max. Bin. Heap (a, n) FOR i : = 2 TO n DO Insert_Max. Bin. Heap(a, i-1, a[i]) ENDFOR 8 7 3 2 4 8 7 5 2 4 3 4 8 3 2 7 5 8 4 3 8 4 2 3 8 7 2 4 3 8 7 5 2 4 3

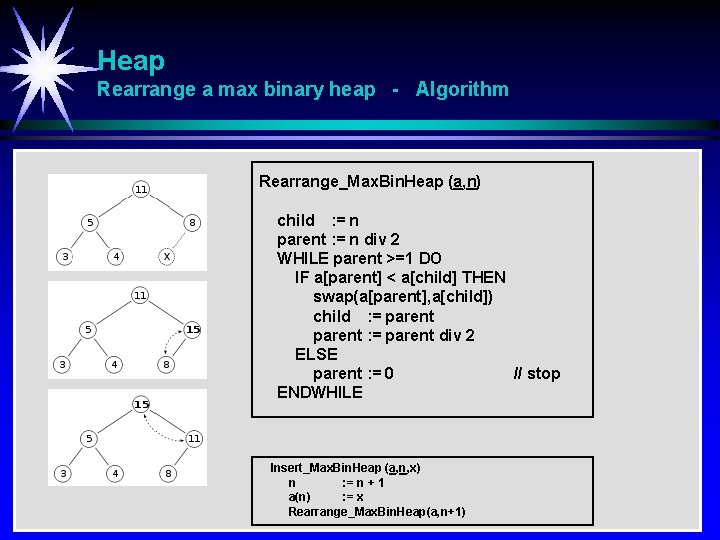
Heap Rearrange a max binary heap - Algorithm Rearrange_Max. Bin. Heap (a, n) child : = n parent : = n div 2 WHILE parent >=1 DO IF a[parent] < a[child] THEN swap(a[parent], a[child]) child : = parent div 2 ELSE parent : = 0 // stop ENDWHILE Insert_Max. Bin. Heap (a, n, x) n : = n + 1 a(n) : = x Rearrange_Max. Bin. Heap(a, n+1)
![Heap Sort Algorithm 12 4 8 3 2 7 5 Heap SortMax Bin Heap. Sort - Algorithm [1/2] 4 8 3 2 7 5 Heap. Sort_Max. Bin.](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-46.jpg)
Heap. Sort - Algorithm [1/2] 4 8 3 2 7 5 Heap. Sort_Max. Bin. Heap (a, n) Build_Max. Bin. Heap(a, n) FOR (i : = n DOWNTO 2) DO swap(a[1], a[i]) Rearrange_Max. Bin. Heap(a, i-1) ENDFOR 8 7 5 2 4 3 swap Rearrange i = 6 3 7 5 2 4 8 7 4 5 2 3 8 i = 5 3 4 5 2 7 8 5 4 3 2 7 8 i = 4 2 4 3 5 7 8 4 2 3 5 7 8 i = 3 3 2 4 5 7 8 i = 2 2 3 4 5 7 8
![8 Heap 8 7 5 2 4 3 Heap Sort Algorithm 22 3 8 Heap 8 7 5 2 4 3 Heap. Sort - Algorithm [2/2] 3](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-47.jpg)
8 Heap 8 7 5 2 4 3 Heap. Sort - Algorithm [2/2] 3 7 7 5 2 4 8 4 5 2 3 8 3 5 4 5 2 7 8 4 3 2 7 8 2 4 4 3 5 7 8 2 3 5 7 8 3 3 2 4 5 7 8 2 2 3 4 5 7 8 7 5 2 4 3 swap Rearrange i = 6 3 7 5 2 4 8 7 4 5 2 3 8 i = 5 3 4 5 2 7 8 5 4 3 2 7 8 i = 4 2 4 3 5 7 8 4 2 3 5 7 8 i = 3 3 2 4 5 7 8 i = 2 2 3 4 5 7 8

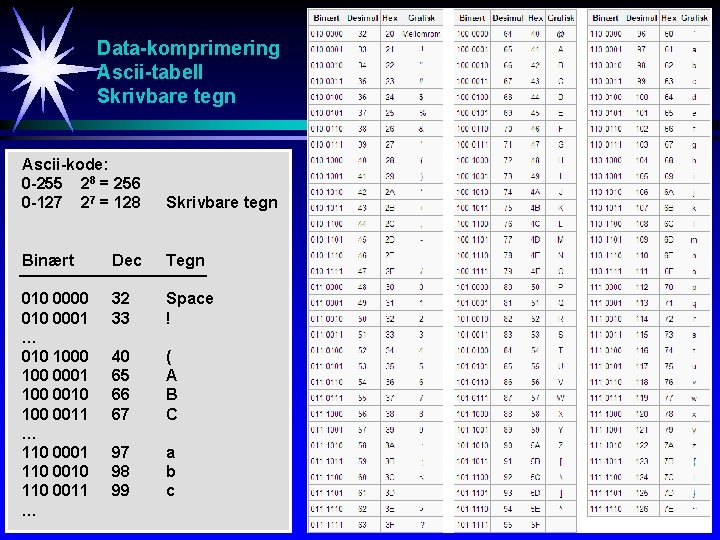
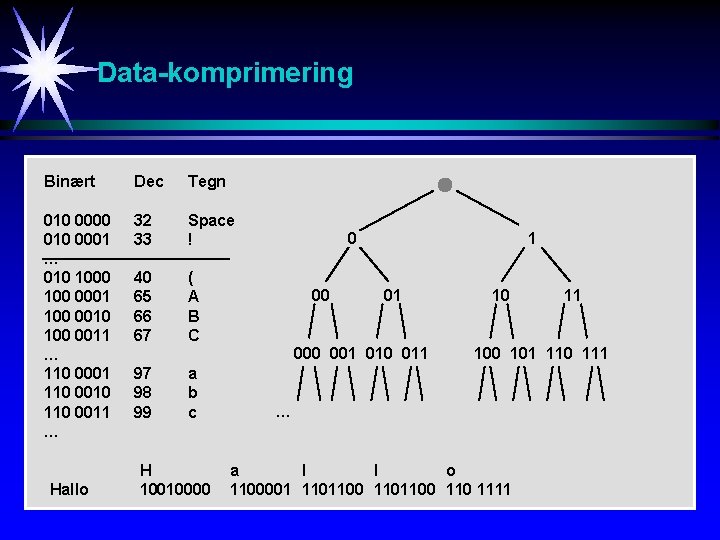
Data-komprimering Ascii-tabell Skrivbare tegn Ascii-kode: 0 -255 28 = 256 0 -127 27 = 128 Skrivbare tegn Binært Dec Tegn 010 0000 010 0001 … 010 100 0001 100 0010 100 0011 … 110 0001 110 0010 110 0011 … 32 33 Space ! 40 65 66 67 ( A B C 97 98 99 a b c

Data-komprimering Binært Dec Tegn 010 0000 010 0001 … 010 100 0001 100 0010 100 0011 … 110 0001 110 0010 110 0011 … 32 33 Space ! 40 65 66 67 ( A B C Hallo 0 00 1 01 000 001 010 011 97 98 99 a b c H 10010000 10 11 100 101 110 111 … a l l o 1100001 1101100 110 1111

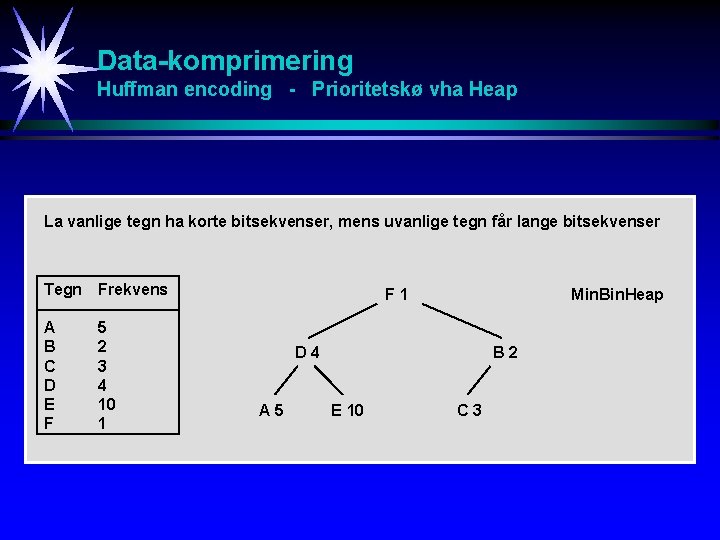
Data-komprimering Huffman encoding - Prioritetskø vha Heap La vanlige tegn ha korte bitsekvenser, mens uvanlige tegn får lange bitsekvenser Tegn Frekvens A B C D E F 5 2 3 4 10 1 F 1 Min. Bin. Heap D 4 A 5 B 2 E 10 C 3

Data-komprimering Huffman encoding - Prioritetskø vha Heap Huffman_Encoding insert all elements into a min. Bin. Heap H according to their frequencies WHILE H is not empty DO IF H contains only one X element THEN make X the root of binary tree T ELSE pick two elements X and Y with lowest frequencies and delete them from H insert a new element Z with f(Z) = f(X) + f(Y) into H insert a new element Z with children X an Y and f(Z) = f(X) + f(Y) into T ENDIF ENDWHILE Z 5 25 E 10 Z 4 15 E 0 Z 2 6 Z 1 3 F 1 Z 3 9 C 3 B 2 1 D 4 10 A 5 100 F 1000 11 C 101 B 1001 D 110 A 111

Symbolsk derivasjon Derivasjon benyttes til å beskrive prosessendringer Typer av diff. lign. ODE Ordinære PDE Partielle Newtons 2. lov Radioaktivitet Kvantefysikk SHM Varmetransport Bølger Elektrisk krets Endringer mht en enkelt variabel Endringer mht flere variabler

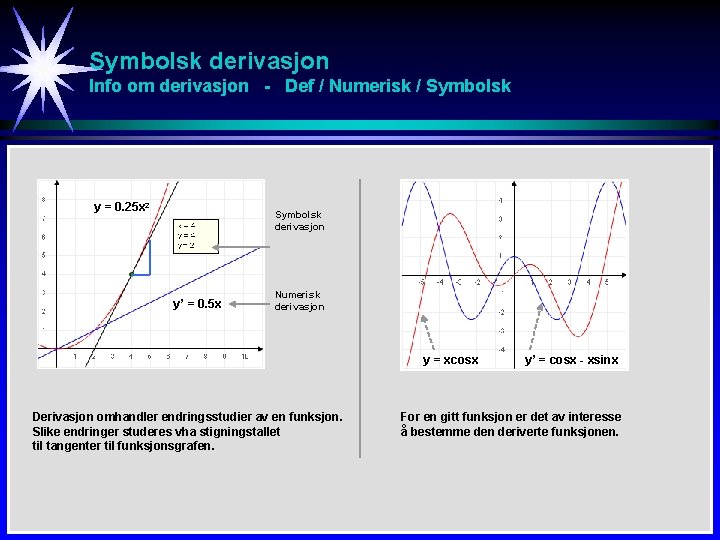
Symbolsk derivasjon Info om derivasjon - Def / Numerisk / Symbolsk y = 0. 25 x 2 Symbolsk derivasjon y’ = 0. 5 x Numerisk derivasjon y = xcosx Derivasjon omhandler endringsstudier av en funksjon. Slike endringer studeres vha stigningstallet til tangenter til funksjonsgrafen. y’ = cosx - xsinx For en gitt funksjon er det av interesse å bestemme den deriverte funksjonen.

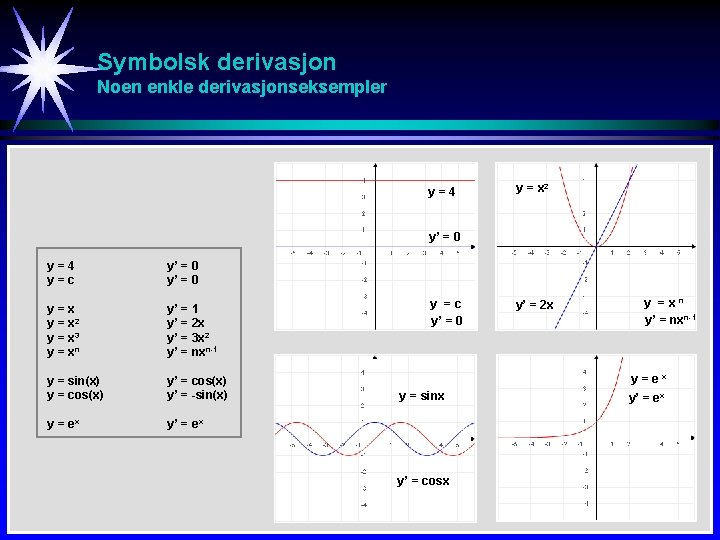
Symbolsk derivasjon Noen enkle derivasjonseksempler y=4 y = x 2 y’ = 0 y=4 y=c y’ = 0 y=x y = x 2 y = x 3 y = xn y’ = 1 y’ = 2 x y’ = 3 x 2 y’ = nxn-1 y = sin(x) y = cos(x) y’ = -sin(x) y = ex y’ = ex y =c y’ = 0 y’ = 2 x y =xn y’ = nxn-1 y=ex y = sinx y’ = cosx y’ = ex

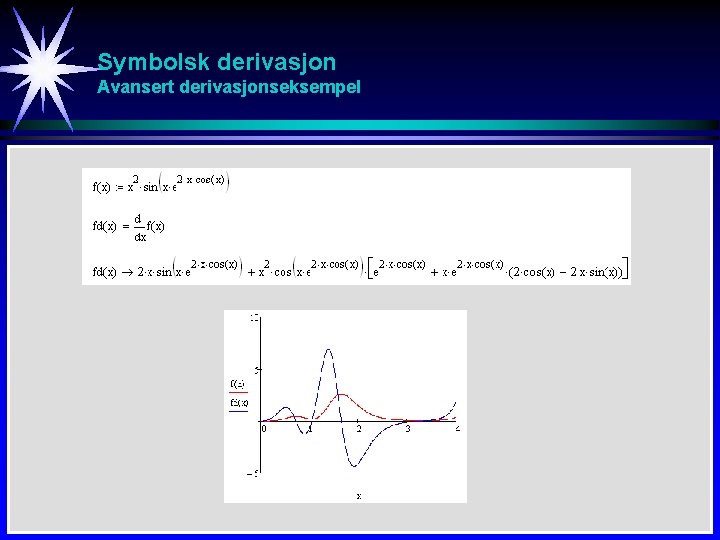
Symbolsk derivasjon Avansert derivasjonseksempel

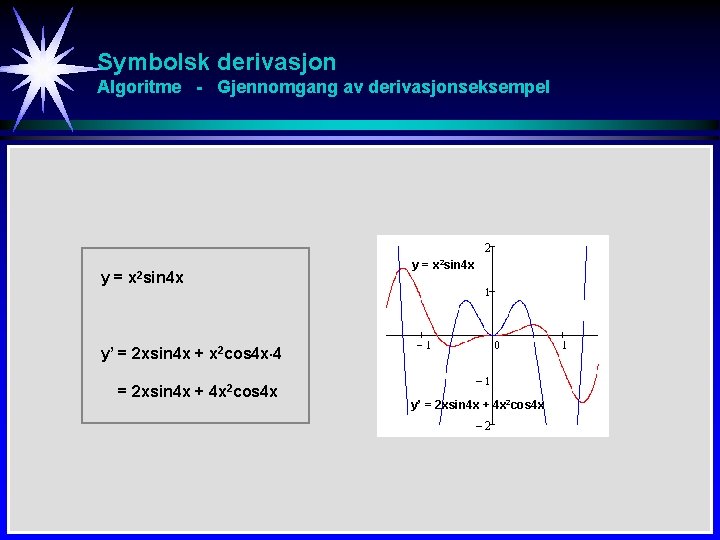
Symbolsk derivasjon Algoritme - Gjennomgang av derivasjonseksempel y= x 2 sin 4 x y’ = 2 xsin 4 x + x 2 cos 4 x 4 = 2 xsin 4 x + 4 x 2 cos 4 x y’ = 2 xsin 4 x + 4 x 2 cos 4 x

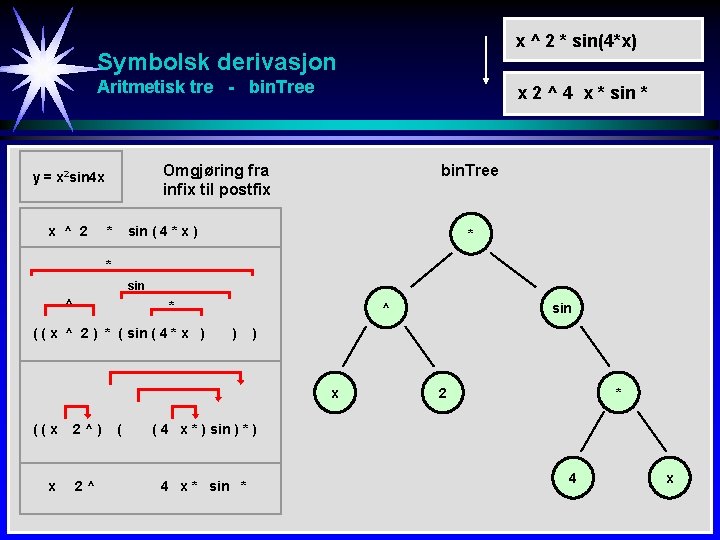
x ^ 2 * sin(4*x) Symbolsk derivasjon Aritmetisk tre - bin. Tree Omgjøring fra infix til postfix y = x 2 sin 4 x x ^ 2 x 2 ^ 4 x * sin * * bin. Tree sin ( 4 * x ) * * sin ^ * ( ( x ^ 2 ) * ( sin ( 4 * x ) ^ ) ) x ((x x 2^) 2^ ( sin 2 * ( 4 x * ) sin ) * ) 4 x * sin * 4 x

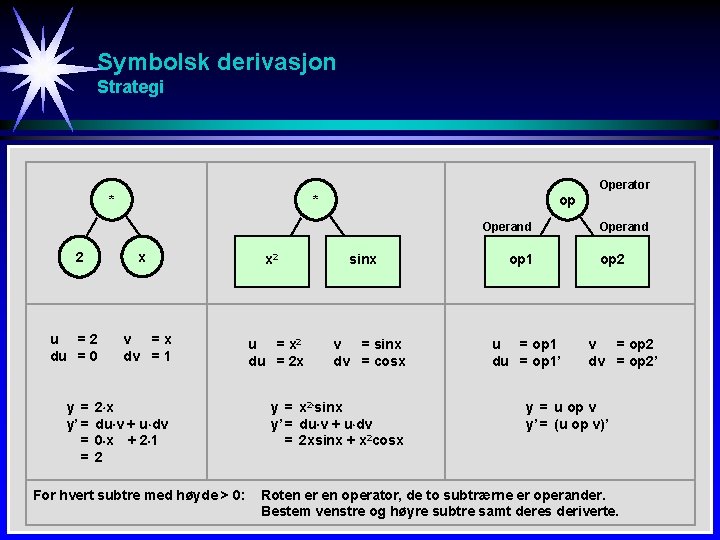
Symbolsk derivasjon Strategi Operator * op * Operand x 2 u =2 du = 0 y = y’ = = = v =x dv = 1 2 x du v + u dv 0 x + 2 1 2 For hvert subtre med høyde > 0: x 2 u = x 2 du = 2 x sinx v = sinx dv = cosx y = x 2 sinx y’ = du v + u dv = 2 xsinx + x 2 cosx op 1 u = op 1 du = op 1’ Operand op 2 v = op 2 dv = op 2’ y = u op v y’ = (u op v)’ Roten er en operator, de to subtrærne er operander. Bestem venstre og høyre subtre samt deres deriverte.

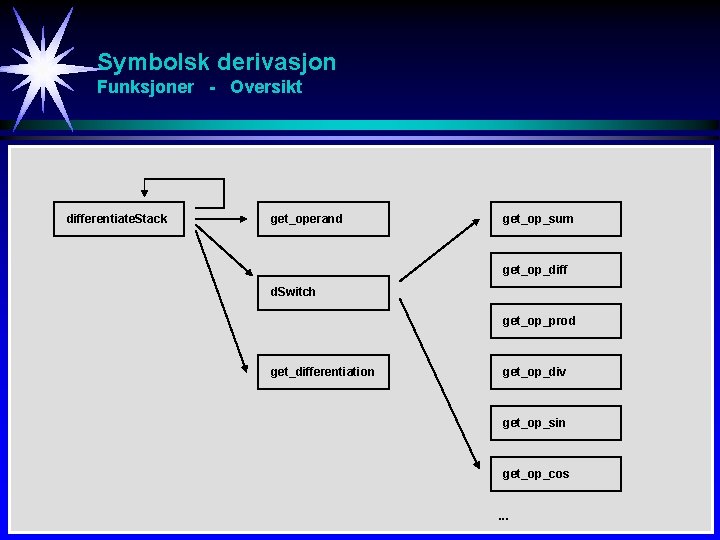
Symbolsk derivasjon Funksjoner - Oversikt differentiate. Stack get_operand get_op_sum get_op_diff d. Switch get_op_prod get_differentiation get_op_div get_op_sin get_op_cos . . .

Symbolsk derivasjon differentiate. Stack

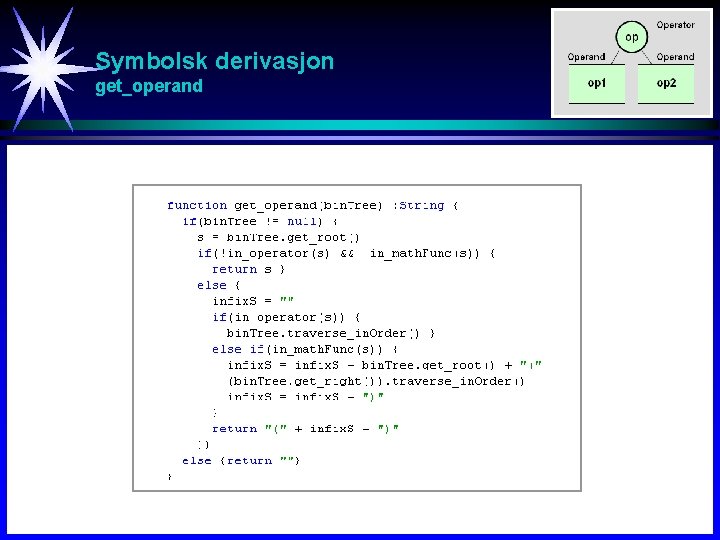
Symbolsk derivasjon get_operand

Symbolsk derivasjon get_differentiation

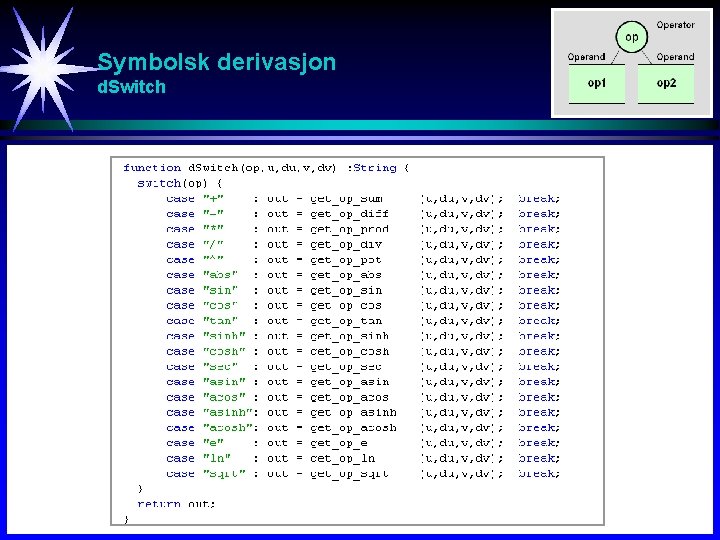
Symbolsk derivasjon d. Switch

Symbolsk derivasjon get_op_. . .

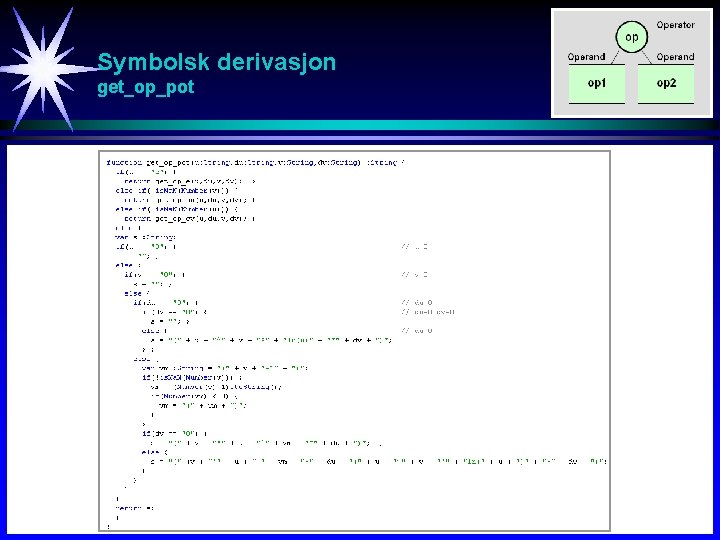
Symbolsk derivasjon get_op_pot

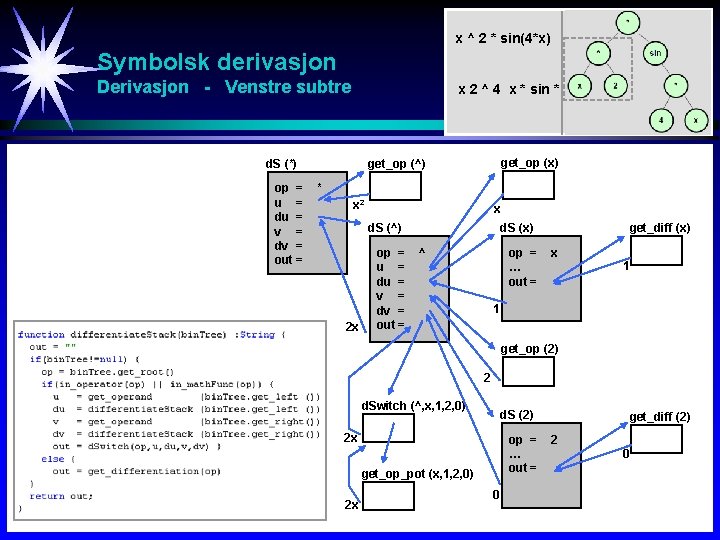
x ^ 2 * sin(4*x) Symbolsk derivasjon y = x 2 sin 4 x Derivasjon - Venstre subtre x 2 ^ 4 x * sin * d. S (*) op = u = du = v = dv = out = get_op (x) get_op (^) * x 2 x d. S (x) d. S (^) 2 x op = u = du = v = dv = out = op = … out = ^ get_diff (x) x 1 1 get_op (2) 2 d. Switch (^, x, 1, 2, 0) d. S (2) 2 x op = … out = get_op_pot (x, 1, 2, 0) 2 x 0 get_diff (2) 2 0

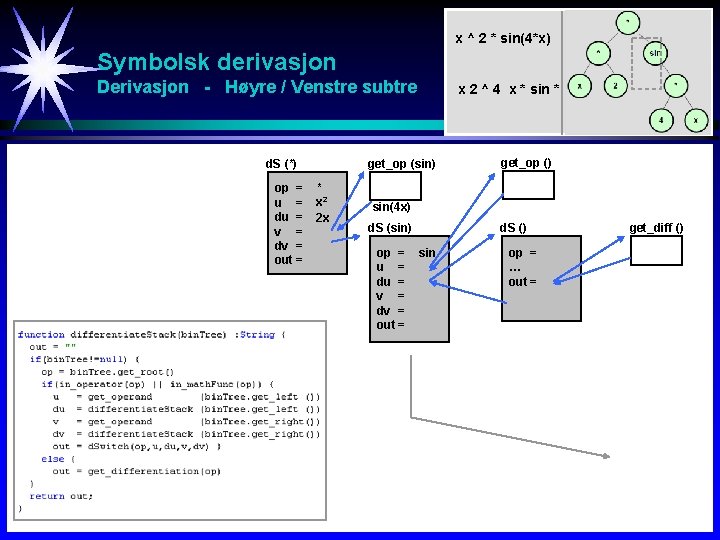
x ^ 2 * sin(4*x) Symbolsk derivasjon y = x 2 sin 4 x Derivasjon - Høyre / Venstre subtre d. S (*) op = u = du = v = dv = out = x 2 ^ 4 x * sin * get_op (sin) * x 2 2 x get_op () sin(4 x) d. S (sin) op = u = du = v = dv = out = sin op = … out = get_diff ()

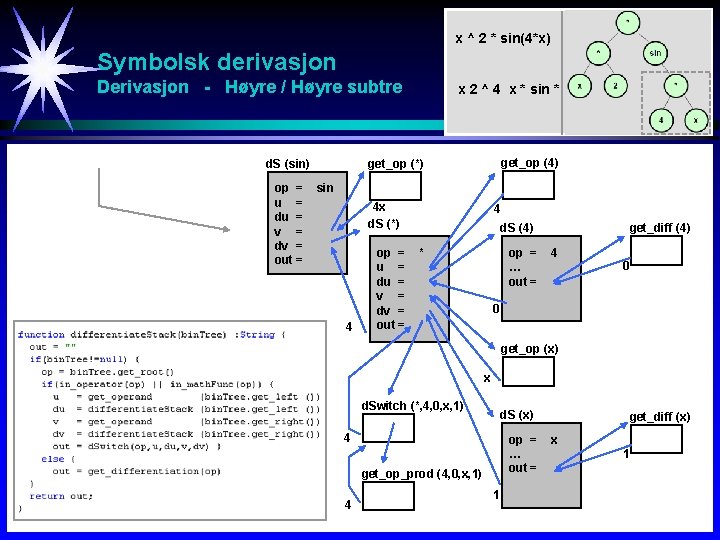
x ^ 2 * sin(4*x) Symbolsk derivasjon y = x 2 sin 4 x Derivasjon - Høyre / Høyre subtre d. S (sin) op = u = du = v = dv = out = x 2 ^ 4 x * sin * get_op (4) get_op (*) sin 4 x d. S (*) 4 op = u = du = v = dv = out = 4 d. S (4) op = … out = * get_diff (4) 4 0 0 get_op (x) x d. Switch (*, 4, 0, x, 1) d. S (x) 4 op = … out = get_op_prod (4, 0, x, 1) 4 1 get_diff (x) x 1

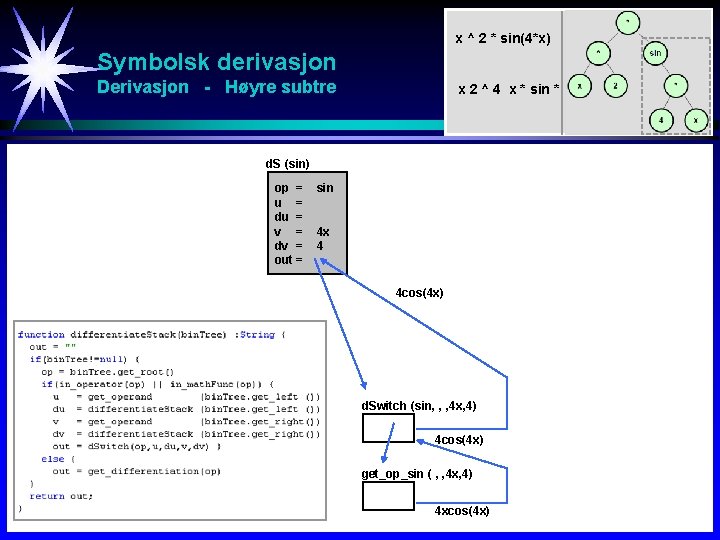
x ^ 2 * sin(4*x) Symbolsk derivasjon y = x 2 sin 4 x Derivasjon - Høyre subtre x 2 ^ 4 x * sin * d. S (sin) op = u = du = v = dv = out = sin 4 x 4 4 cos(4 x) d. Switch (sin, , , 4 x, 4) 4 cos(4 x) get_op_sin ( , , 4 x, 4) 4 xcos(4 x)

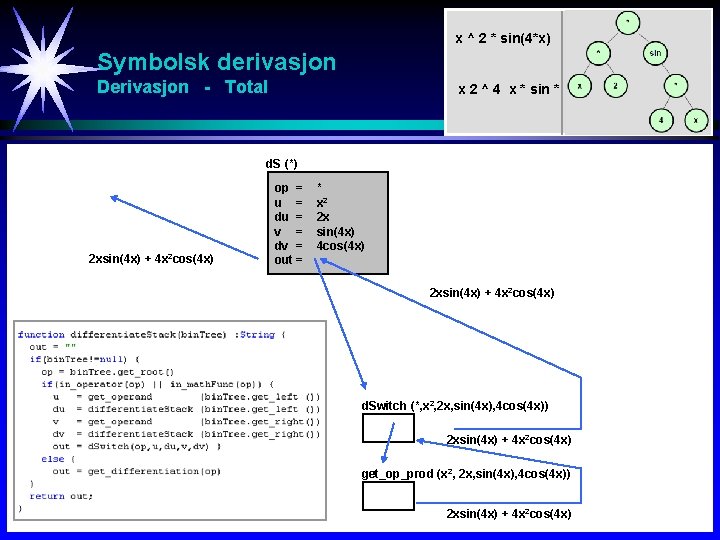
x ^ 2 * sin(4*x) Symbolsk derivasjon y = x 2 sin 4 x Derivasjon - Total x 2 ^ 4 x * sin * d. S (*) 2 xsin(4 x) + 4 x 2 cos(4 x) op = u = du = v = dv = out = * x 2 2 x sin(4 x) 4 cos(4 x) 2 xsin(4 x) + 4 x 2 cos(4 x) d. Switch (*, x 2, 2 x, sin(4 x), 4 cos(4 x)) 2 xsin(4 x) + 4 x 2 cos(4 x) get_op_prod (x 2, 2 x, sin(4 x), 4 cos(4 x)) 2 xsin(4 x) + 4 x 2 cos(4 x)

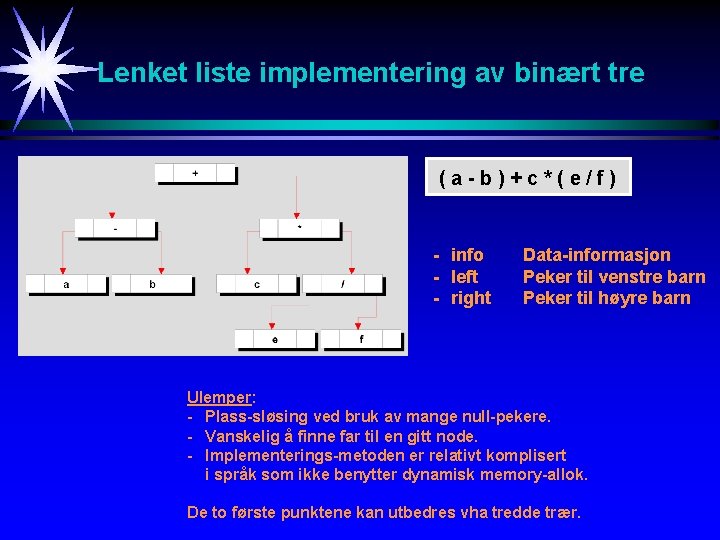
Lenket liste implementering av binært tre (a-b)+c*(e/f) - info - left - right Data-informasjon Peker til venstre barn Peker til høyre barn Ulemper: - Plass-sløsing ved bruk av mange null-pekere. - Vanskelig å finne far til en gitt node. - Implementerings-metoden er relativt komplisert i språk som ikke benytter dynamisk memory-allok. De to første punktene kan utbedres vha tredde trær.

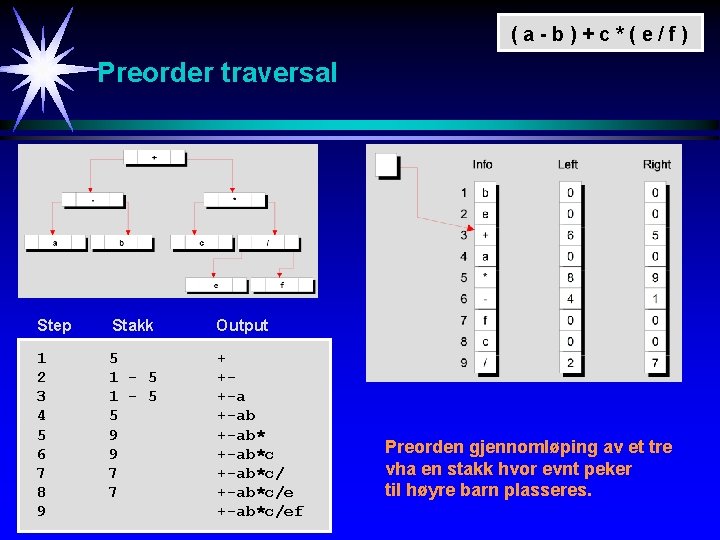
(a-b)+c*(e/f) Preorder traversal Step Stakk Output 1 2 3 4 5 6 7 8 9 5 1 - 5 5 9 9 7 7 + ++-a +-ab*c/ +-ab*c/ef Preorden gjennomløping av et tre vha en stakk hvor evnt peker til høyre barn plasseres.

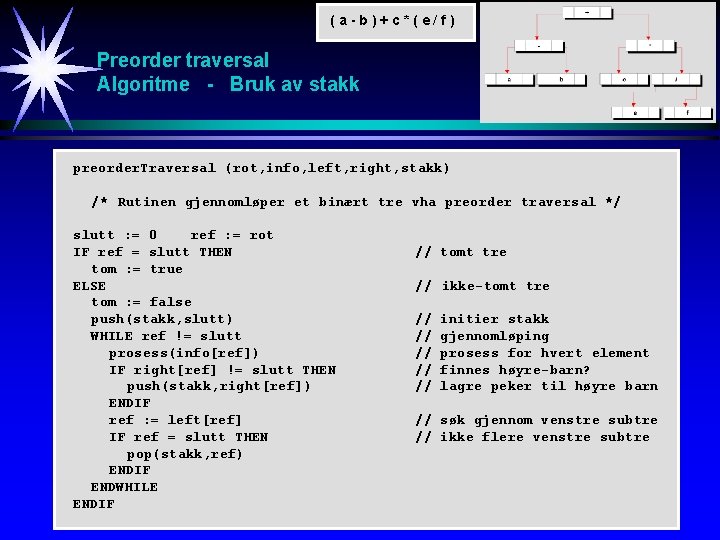
(a-b)+c*(e/f) Preorder traversal Algoritme - Bruk av stakk preorder. Traversal (rot, info, left, right, stakk) /* Rutinen gjennomløper et binært tre vha preorder traversal */ slutt : = 0 ref : = rot IF ref = slutt THEN tom : = true ELSE tom : = false push(stakk, slutt) WHILE ref != slutt prosess(info[ref]) IF right[ref] != slutt THEN push(stakk, right[ref]) ENDIF ref : = left[ref] IF ref = slutt THEN pop(stakk, ref) ENDIF ENDWHILE ENDIF // tomt tre // ikke-tomt tre // // // initier stakk gjennomløping prosess for hvert element finnes høyre-barn? lagre peker til høyre barn // søk gjennom venstre subtre // ikke flere venstre subtre

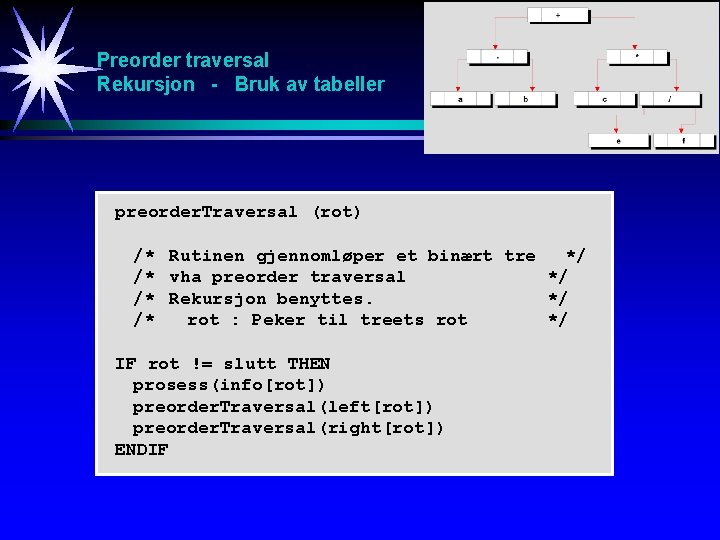
Preorder traversal Rekursjon - Bruk av tabeller preorder. Traversal (rot) /* Rutinen gjennomløper et binært tre */ /* vha preorder traversal */ /* Rekursjon benyttes. */ /* rot : Peker til treets rot */ IF rot != slutt THEN prosess(info[rot]) preorder. Traversal(left[rot]) preorder. Traversal(right[rot]) ENDIF

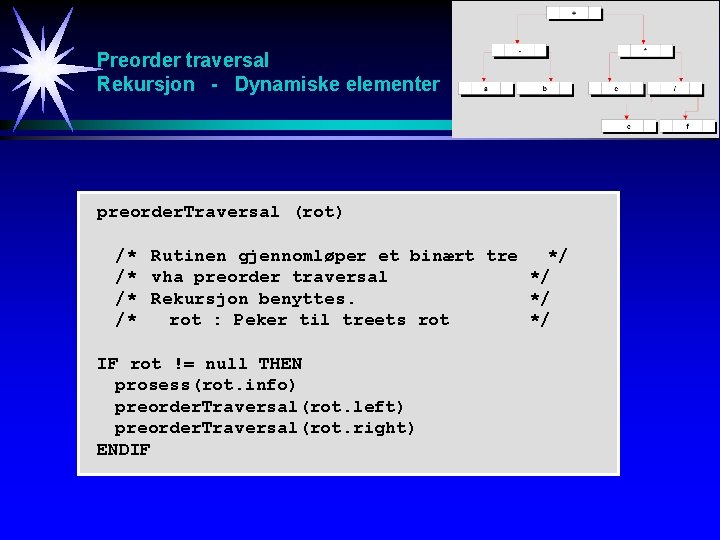
Preorder traversal Rekursjon - Dynamiske elementer preorder. Traversal (rot) /* Rutinen gjennomløper et binært tre */ /* vha preorder traversal */ /* Rekursjon benyttes. */ /* rot : Peker til treets rot */ IF rot != null THEN prosess(rot. info) preorder. Traversal(rot. left) preorder. Traversal(rot. right) ENDIF

Preorder – Inorder – Postorder traversal IF rot != null THEN prosess(rot. info) preorder. Traversal(rot. left) preorder. Traversal(rot. right) ENDIF Preorder IF rot != null THEN inorder. Traversal(rot. left) prosess(rot. info) inorder. Traversal(rot. right) ENDIF Inorder Postorder IF rot != null THEN postorder. Traversal(rot. left) postorder. Traversal(rot. right) prosess(rot. info) ENDIF

Sortering vha binært tre Et binært tre sies å være sortert (i stigende rekkefølge) når følgende er oppfylt: Til enhver node med innhold N vil: - venstre subtre kun inneholde elementer som er mindre enn N - høyre subtre kun inneholde elementer som er større enn eller lik N Dette medfører at i et sortert binært tre vil inorden traversering gi elementene i sortert rekkefølge.

Sortering vha binært tre 19 - 5 - 10 - 7 - 25 - 8 - 15 - 90 - 12 - 2 1. 2. 3. 4. 5. . Første tall (her 19) plasseres i treets rot. Neste tall 5 leses. Siden 5 er mindre enn 19, plasseres 5 som venstre barn til 19. Tallet 10 leses. 10 er mindre enn 19, derfor går vi til venstre for 19. 10 er større enn 5, derfor plasseres 10 som høyre barn til 5.

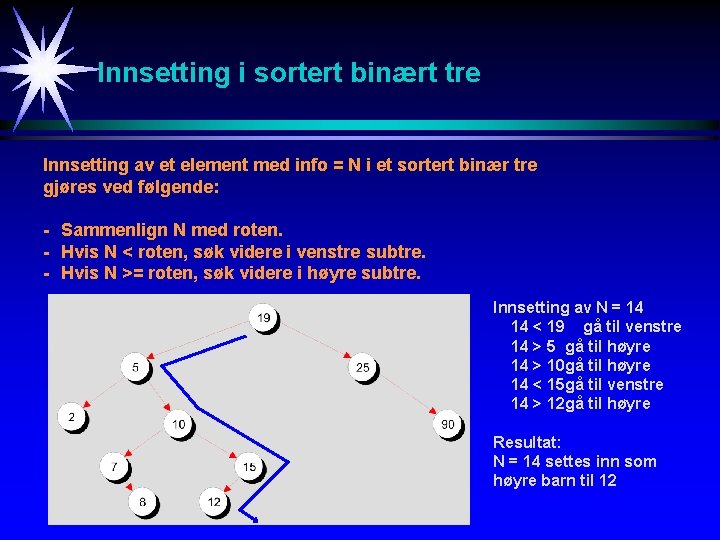
Innsetting i sortert binært tre Innsetting av et element med info = N i et sortert binær tre gjøres ved følgende: - Sammenlign N med roten. - Hvis N < roten, søk videre i venstre subtre. - Hvis N >= roten, søk videre i høyre subtre. Innsetting av N = 14 14 < 19 gå til venstre 14 > 5 gå til høyre 14 > 10 gå til høyre 14 < 15 gå til venstre 14 > 12 gå til høyre Resultat: N = 14 settes inn som høyre barn til 12

Innsetting i et sortert binært tre Algoritme Innsett (info, left, right, led, post, rot, full) NULL : = 0 IF Led = NULL THEN Full : = True ELSE Full : = False Ny : = Led : = Left[ny] Info[Ny] : = Post Left[Ny] : = NULL Right[ny]: = NULL IF Rot = NULL THEN Rot : = Ny ELSE Peker : = Rot WHILE Peker <> NULL DO Forrige : = Peker IF Post < Info[Peker] THEN Peker : = Left[Peker] ELSE Peker : = Right[Peker] ENDIF ENDWHILE IF Post < Info[Forrige] THEN Left[Forrige] : = Ny ELSE Right[Forrige] : = Ny ENDIF // Treet er fullt // Ledig plass i treet // Plasser ny post // Ajourfør ledig-listen // Innsett data i ny post // Opprinnelig tomt tre // Innsetting i ikke-tomt tre // Søk nedover i treet // Til venstre // Til høyre // Pekere til ny post

Slettting i binært tre Inorden gjennomløping av det binære treet gir elementene i sortert rekkefølge: Grete, Kari, Kjell, Lars, Martin, Nils, Ola, Per, Renate, Rolf, Stine, Truls, Åse. Stine skal fjernes. Dette kan løses på to måter: - Erstatt Stine med største element i venstre subtre hvor Stine er rot, dvs Rolf. - Erstatt Stine med minste element i høyre subtre hvor Stine er rot, dvs Trine.

Sletting i binært tre Stine skal fjernes. Erstatt Stine med største element i venstre subtre hvor Stine er rot, dvs Rolf.

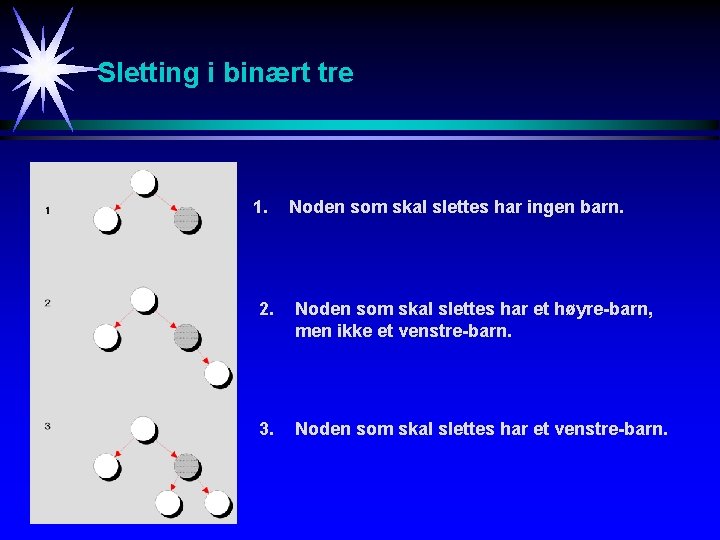
Sletting i binært tre 1. Noden som skal slettes har ingen barn. 2. Noden som skal slettes har et høyre-barn, men ikke et venstre-barn. 3. Noden som skal slettes har et venstre-barn.

Sletting i et sortert binært tre - Algoritme Case 1: Noden som skal slettes har ingen barn p. Pek sletting_1 (info, left, right, spek, p. Pek, rot, led) null : = 0 IF ppek = null THEN rot : = null ELSE IF s. Pek = Left[p. Pek] THEN left[p. Pek] : = null ELSE right[p. Pek] : = null ENDIF left[s. Pek] : = led : = s. Pek // Fjerning av rot // Forelder finnes // Ledigliste s. Pek

Sletting i et sortert binært tre - Algoritme Case 2: Noden som skal slettes har et høyre-barn, men ikke et venstre-barn p. Pek sletting_2 (info, left, right, spek, p. Pek, rot, led) null : = 0 IF ppek = null THEN // Fjerning av rot : = right[s. Pek] ELSE // Forelder finnes IF s. Pek = Left[p. Pek] THEN left[p. Pek] : = right[s. Pek] ELSE right[p. Pek] : = right[s. Pek] ENDIF left[s. Pek] : = led // Ledigliste led : = s. Pek Case 1 er et spesialtilfelle av Case 2

Sletting i et sortert binært tre - Algoritme Case 3. 1: Noden som skal slettes har et venstre-barn. Venstre-barn til noden som skal slettes har ikke høyrebarn. p. Pek sletting_3_1 (info, left, right, spek, p. Pek, rot, led) null : = 0 peker : = left[s. Pek] IF ppek = NULL THEN rot : = peker ELSE IF left[p. Pek] = s. Pek THEN left[p. Pek] : = peker ELSE right[p. Pek] : = peker ENDIF right[peker] : = right[s. Pek] left[s. Pek] : = led : = s. Pek // erst. slettet e. // Fjerning av rot // Forelder finnes s. Pek // Flyttet element // Ledigliste

Sletting i et sortert binært tre - Algoritme Case 3. 2: Noden som skal slettes har et venstre-barn. Venstre-barn til noden som skal slettes har høyre-barn. p. Pek sletting_3_2 (info, left, right, spek, p. Pek, rot, led) null : = 0 peker : = left[s. Pek] forrige : = peker WHILE right[peker] != null forrige : = peker : = right[peker] ENDWHILE IF ppek = NULL THEN rot : = peker ELSE IF left[p. Pek] = s. Pek THEN left[p. Pek] : = peker ELSE right[p. Pek] : = peker ENDIF right[peker] : = right[s. Pek] right[forrige] : = left[peker] : = left[s. Pek] : = led : = s. Pek // Fjerning av rot // Forelder finnes // Ledigliste s. Pek

Ulike strukturer av binært tre I et tre (her binært tre) kan det av og til være ønskelig med ekstra pekere bl. a. for å lette gjennomløping av et slikt tre.

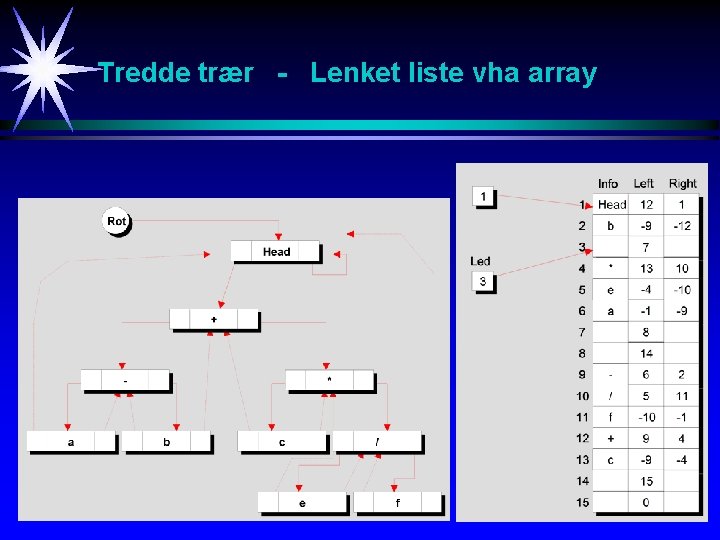
Tredde trær I såkalte tredde trær benyttes såkalte Tpekere (opprinnelige null-pekere fra løv-noder) til å peke oppover i treet igjen, dette bl. a. for å lette gjennomløping av et slikt tre. Tpekere settes negative. En Tpeker som erstatter en left. Peker, peker til foregående node og en Tpeker som erstatter en right. Peker, peker til neste node (begge ved inorden gjennomløping. Ytterste venstre og høyre Tpeker tilbake til roten.

Tredde trær - Tomt tre med dummynode Et tomt tredd tre med dummynode. Det er hensiktsmessig å la høyre Tpeker være en ordinær peker, dvs høyre Tpeker er positiv. Head

Tredde trær - Lenket liste vha array

Tredde trær tredd. Inorder - Algoritme tredd. Inorder (info, left, right, rot, tom) peker : = rot IF Abs(left[peker]) = rot THEN tom : = true ELSE tom : = false REPEAT IF right[peker] < 0 THEN peker : = abs(right[peker]) ELSE peker : = right[peker] WHILE left[peker] > 0 DO peker : = left[peker] ENDWHILE ENDIF IF peker <> rot THEN prosess(info[peker]) ENDIF UNTIL peker = rot ENDIF // tomt tre // Ikke-tomt tre // Tpeker // Ordinær peker // Søk nedover til venstre // Reell node // Hele treet gjennomløpt

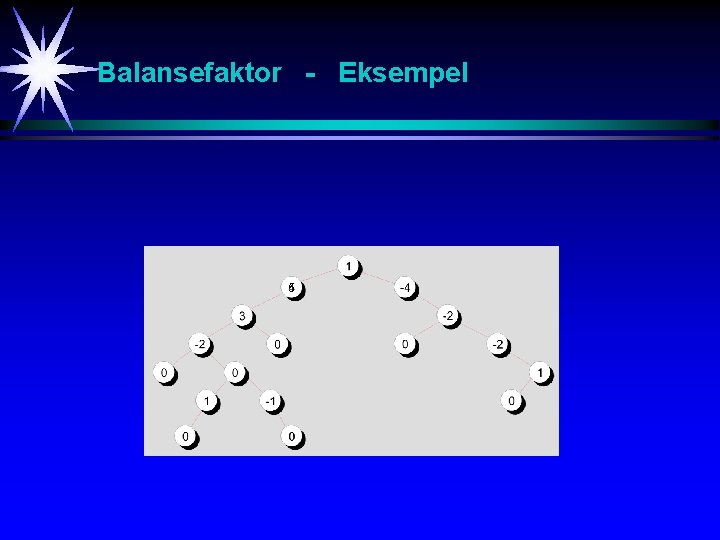
Balanserte trær For å minimalisere gjennomsnittlig søke-lengde etter en gitt node i et tre, er det viktig at venstre og høyre subtre til en node er av tilnærmet samme lengde. For å kontrollere ulikheter i lengden av venstre/høyre subtre, innføres for hver node en såkalt balansefaktor (BF). BF = lengden av venstre subtre - lengden av høyre subtre Et tre sies å være balansert hvis alle noder har en balansefaktor BF = -1, 0, 1

Balansefaktor - Eksempel 5

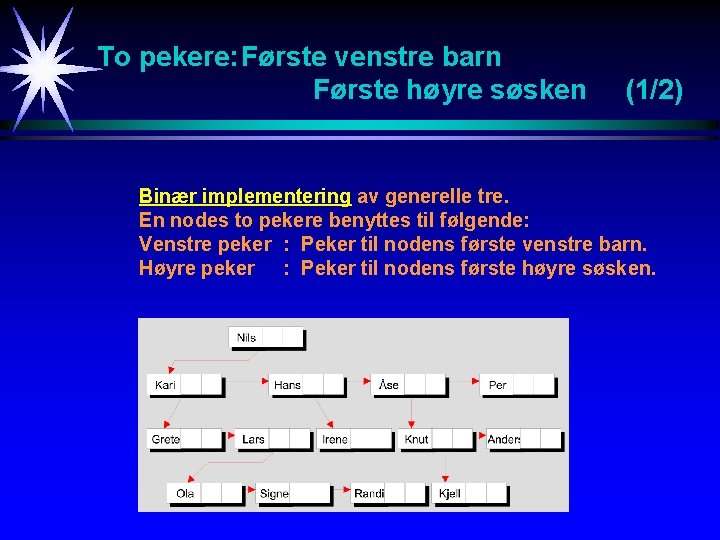
AVL-rotasjon Ved innsetting gjøres følgende: 1. La nytt element gjennomløpe greinene inntil innsettingspunkt er funnet. Samtidig merkes av siste node hvor opprinnelig balansefaktor er +1 eller -1. Denne noden kalles for PIVOT-noden. Innsett nytt element på korrekt plass. 2. Korriger balansefaktoren for PIVOT-noden og samtlige noder i det subtreet som har PIVOT-noden som rot. Det kan vises at ingen andre noder i treet får sin balansefaktor endret ved AVL-rotasjoner. 3. Hvis absoluttverdien av balansefaktoren for PIVOT-noden ble endret fra 1 til 2, så skal subtreet hvor PIVOT-noden er rot gjennomgå en AVL-rotasjon. Dette gjøres ved å endre pekere, men på en slik måte at treet’s ordnings-rekkefølge blir uendret.
![Case 1 Innsetting i venstre subtre til venstre barn til Pivotnode 12 Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [1/2]](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-96.jpg)
Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [1/2]
![Case 1 Innsetting i venstre subtre til venstre barn til Pivotnode 22 l Pek Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [2/2] l. Pek](https://slidetodoc.com/presentation_image/2f01566992a38d732d57d7ed25bc4cfc/image-97.jpg)
Case 1: Innsetting i venstre subtre til venstre barn til Pivot-node [2/2] l. Pek (1) 4 AVL_Left (left, right, bf, pivot) 3 pivot (5) r. Pek (2) /* AVL_Left-rotasjon */ /* left Tabell med venstre-peker*/ /* right Tabell med høyre-peker */ /* bf Tabell med balansefaktor */ /* pivot Peker til pivot-node */ l. Pek right[l. Pek] left[pivot bf[pivot] bf[right[pivot]] : = left[pivot] : = right[l. Pek] : = pivot : = r. Pek : = l. Pek : = 0 // 1 // 2 // 3 // 4 // 5 // 6 // 7

Case 2: Innsetting i høyre subtre til høyre barn til Pivot-node

Case 3. 1: Innsetting i høyre subtre til venstre barn til Pivot-node

Case 3. 2: Innsetting i venstre subtre til høyre barn til venstre barn til Pivot-node

Case 3. 3: Innsetting i høyre subtre til høyre barn til venstre barn til Pivot-node

Case 4: Innsetting i venstre subtre til høyre barn til Pivot-node Algoritmene til Case 4 blir analoge med algoritmene til Case 3.

Generell tre I et binært tre har hver node maksimalt to barn. I et generelt tre har hver node et vilkårlig antall barn. Ethvert generelt tre kan implementeres som et binært tre.

Variabelt antall pekere til barn Generelt tre hvor hver node har et variabelt antall pekere til barna.

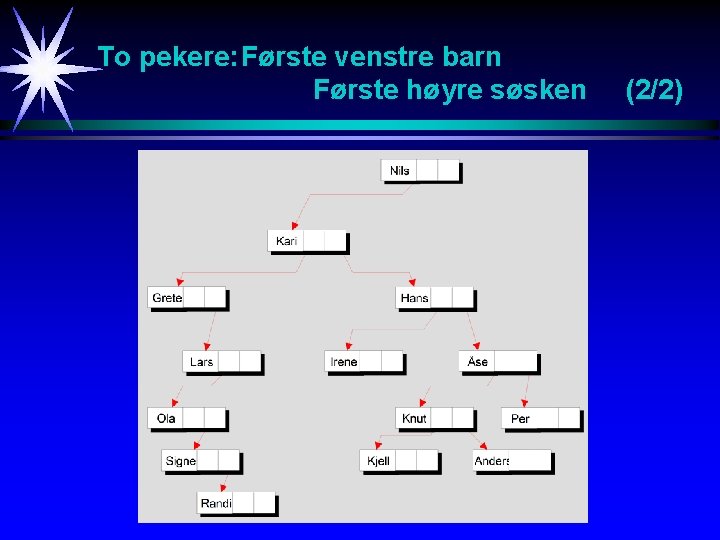
To pekere: Første venstre barn Første høyre søsken (1/2) Binær implementering av generelle tre. En nodes to pekere benyttes til følgende: Venstre peker : Peker til nodens første venstre barn. Høyre peker : Peker til nodens første høyre søsken.

To pekere: Første venstre barn Første høyre søsken (2/2)

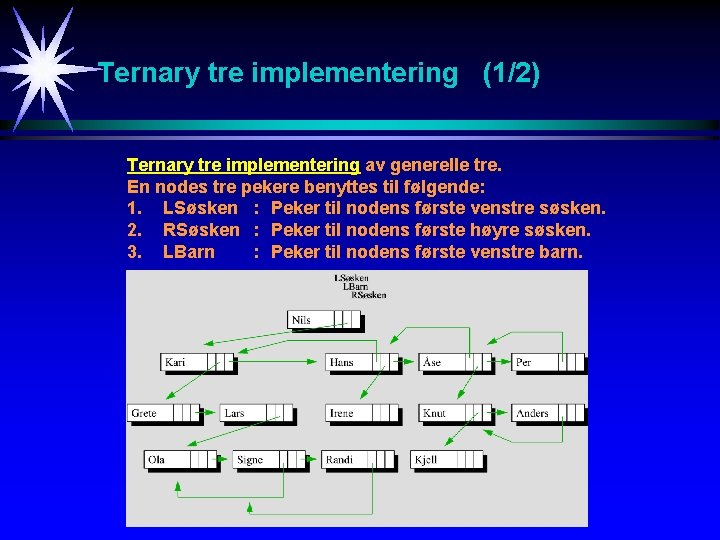
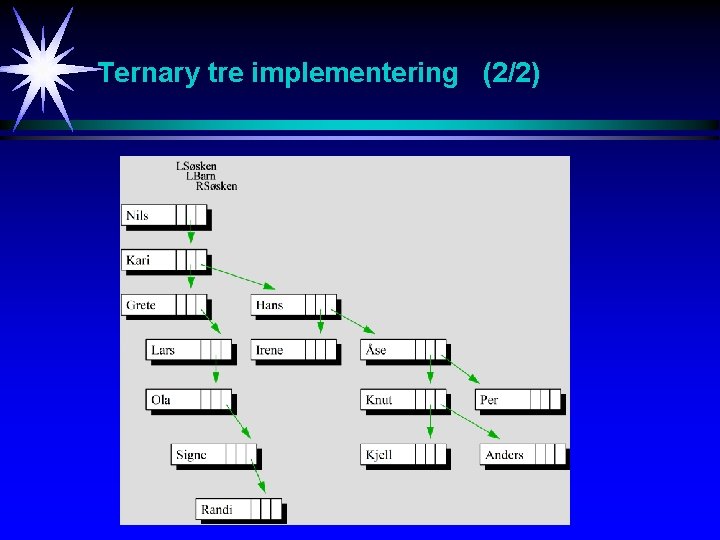
Ternary tre implementering (1/2) Ternary tre implementering av generelle tre. En nodes tre pekere benyttes til følgende: 1. LSøsken : Peker til nodens første venstre søsken. 2. RSøsken : Peker til nodens første høyre søsken. 3. LBarn : Peker til nodens første venstre barn.

Ternary tre implementering (2/2)

Hierarkisk datastruktur - Bil Tre-struktur / Hierarkisk struktur benyttes ofte der hvor det er aktuelt å få svar på spørsmål av typen: - Gitt et objekt, hvilke komponenter består objektet av ? - Gitt et objekt, hvilket større objekt er dette en del av ?

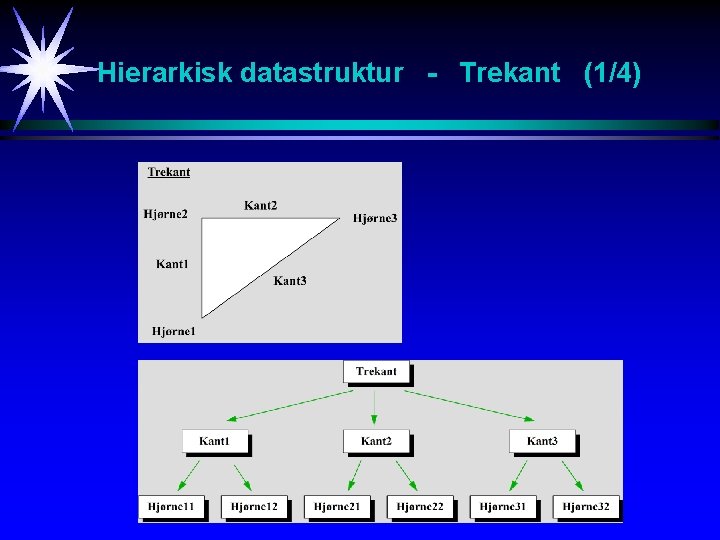
Hierarkisk datastruktur - Trekant (1/4)

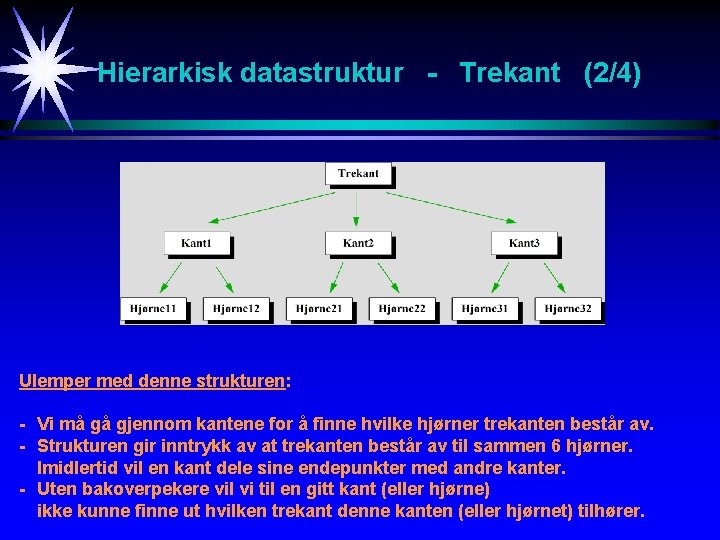
Hierarkisk datastruktur - Trekant (2/4) Ulemper med denne strukturen: - Vi må gå gjennom kantene for å finne hvilke hjørner trekanten består av. - Strukturen gir inntrykk av at trekanten består av til sammen 6 hjørner. Imidlertid vil en kant dele sine endepunkter med andre kanter. - Uten bakoverpekere vil vi til en gitt kant (eller hjørne) ikke kunne finne ut hvilken trekant denne kanten (eller hjørnet) tilhører.

Hierarkisk datastruktur - Trekant (3/4) - Vi tar utgangs-punkt i at en trekant består av 3 kanter og 3 hjørner. - Videre ønsker vi mulighet for raskt å kunne scanne igjennom kantene/hjørnene til en gitt trekant. - Uansett hvor vi kommer inn på kant/hjørne skal vi raskt kunne scanne igjennom de øvrige kantene/hjørnene. - For gitt kant/hjørne skal vi raskt kunne finne ut hvilken trekant denne tilhører. Siden det til hver kant finnes to endepunkter, kan vi bestemme foreldre-elementet til en gitt kant ved å gå gjennom ett av endepunktene. Dette vil spare lagerplass. - For gitt kant skal vi raskt kunne bestemme denne kantens endepunkter. - En trekant kan vi tenke oss som en del av et større geometrisk objekt bestående av flere elementer. For hver trekant ønsker vi derfor en peker til neste element.

Hierarkisk datastruktur - Trekant (4/4) Trekant: - Type - Peker til første kant - Peker til første hjørne - Peker til neste element Hjørne: - Type - XKoordinat - YKoordinat - Peker til neste hjørne - Peker til foreldre Kant: - Type - Peker til endepunt 1 - Peker til endepunt 2 - Peker til neste kant

Hierarkisk datastruktur - Multiple trekanter Trekant: - Type - Peker til første kant - Peker til første hjørne - Peker til neste element Hjørne: - Type - XKoordinat - YKoordinat - Peker til neste hjørne - Peker til foreldre Kant: - Type - Peker til endepunt 1 - Peker til endepunt 2 - Peker til neste kant - Peker tilsluttet kant - Peker til nabo-trekant

Hierarkisk datastruktur - Grafisk system Trekant: - Type - Peker til første kant - Peker til første hjørne - Peker til neste element Hjørne: - Type - XKoordinat - YKoordinat - Peker til neste hjørne - Peker til foreldre Kant: - Type - Peker til endepunt 1 - Peker til endepunt 2 - Peker til neste kant - Peker tilsluttet kant - Peker til nabo-trekant

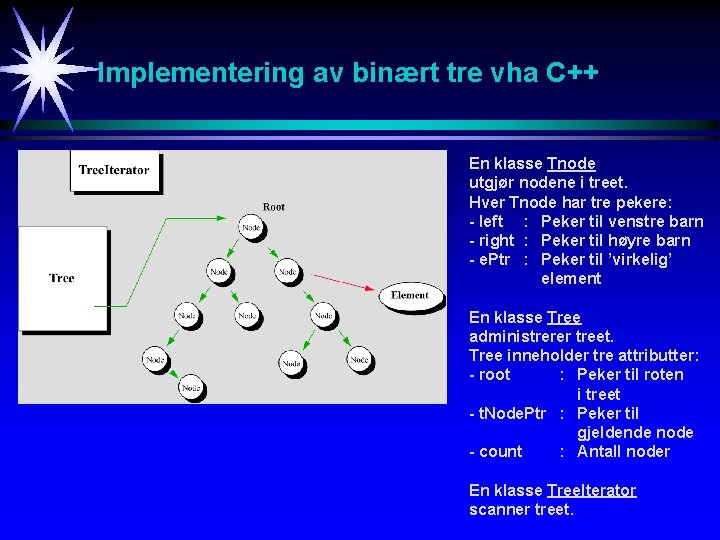
Implementering av binært tre vha C++ En klasse Tnode utgjør nodene i treet. Hver Tnode har tre pekere: - left : Peker til venstre barn - right : Peker til høyre barn - e. Ptr : Peker til ’virkelig’ element En klasse Tree administrerer treet. Tree inneholder tre attributter: - root : Peker til roten i treet - t. Node. Ptr : Peker til gjeldende node - count : Antall noder En klasse Tree. Iterator scanner treet.

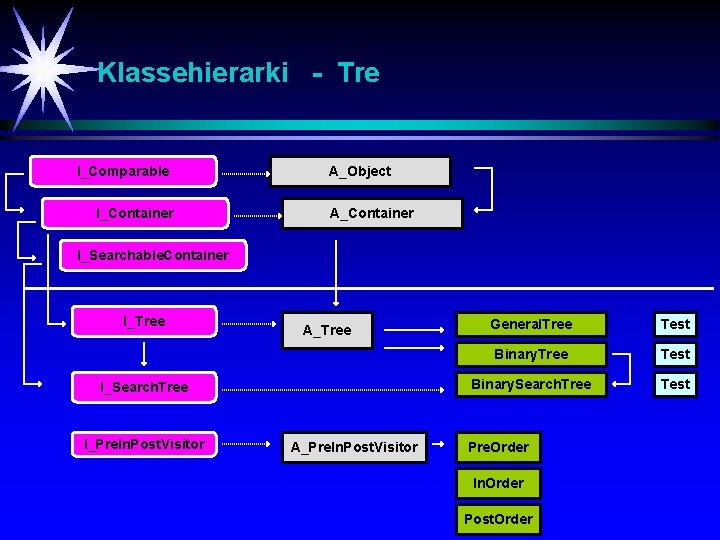
Klassehierarki - Tre I_Comparable I_Container A_Object A_Container I_Searchable. Container I_Tree A_Tree I_Search. Tree I_Pre. In. Post. Visitor A_Pre. In. Post. Visitor General. Tree Test Binary. Search. Tree Test Pre. Order In. Order Post. Order

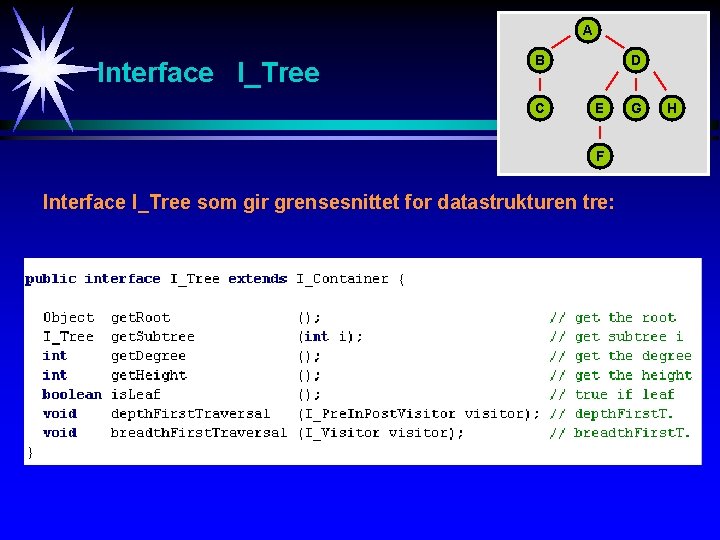
A Interface I_Tree B C D E F Interface I_Tree som gir grensesnittet for datastrukturen tre: G H

A depth. First. Traversal B C depth. First. Traversal omfatter de tre spesialtilfellene: - Pre. Order - In. Order (kun for binære trær) - Post. Order D E G F For å kunne håndtere disse tre spesialtilfellene, benytter depth. First. Traversal parametertypen I_Pre. In. Post. Visitor. For å kunne sende en I_Visitor til depth. First. Traversal lages en såkalt adapter (konverterer et interface nødvendig for en klasse over til et annet interface nødvendig for en annen klasse). Vi benytter 3 slike adaptere: Klassene Pre. Order, In. Order og Post. Order som alle implementerer I_Pre. In. Post. Visitor. I_Visitor v = new …Visitor( ); I_Tree t = new …Tre( ); … t. depth. First. Traversal (new Pre. Order(v)); … H

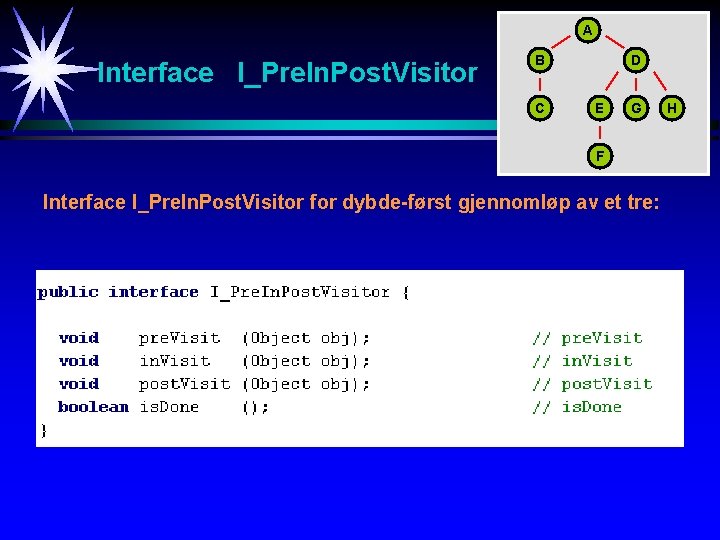
A Interface I_Pre. In. Post. Visitor B C D E G F Interface I_Pre. In. Post. Visitor for dybde-først gjennomløp av et tre: H

Abstract class A_Pre. In. Post. Visitor

class Pre. Order

class In. Order

class Post. Order

A abstract class A_Tree depth. First. Traversal B C D E F G H

A abstract class A_Tree breadth. First. Traversal B C D E F G H

A abstract class A_Tree B D accept C E F G H

A abstract class A_Tree B D get. Enumeration C E F En parameter visitor av typen I_Pre. In. Post. Visitor følger med. G H

A abstract class A_Tree B D Tree. Enumeration C E F G H

A abstract class A_Tree B Tree. Enumeration has. More. Elements - next. Element C D E F G H

A abstract class A_Tree B get. Root – get. Subtree get. Degree- get. Height - is. Leaf C D E F G H

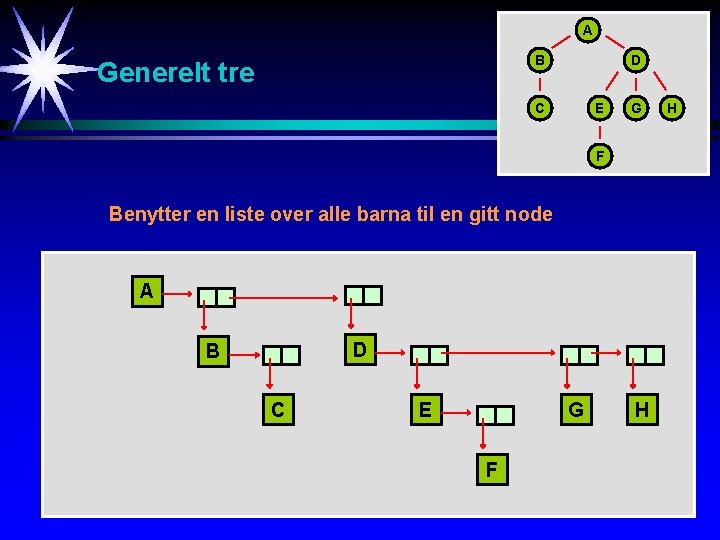
A B Generelt tre D C E G F Benytter en liste over alle barna til en gitt node A D B C E G F H H

A Generelt tre B D constructor C E F G H

A Generelt tre get. Root - get. Degree - get. Subtree B C D E F G H

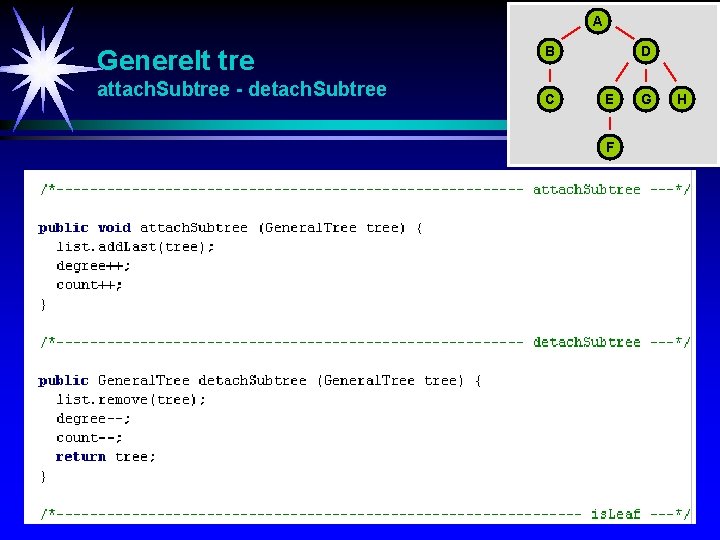
A Generelt tre attach. Subtree - detach. Subtree B C D E F G H

A Generelt tre is. Leaf - is. Empty - remove. All B C D E F G H

A Test Generelt tre (1/2) B D C

A Test Generelt tre (2/2) B D C

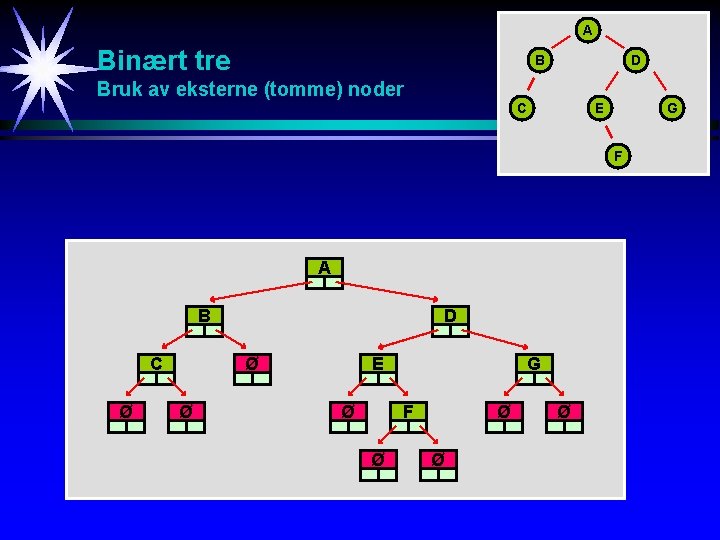
A Binært tre B D Bruk av eksterne (tomme) noder C E G F A B C Ø D Ø Ø E Ø G F Ø Ø

A Binært tre constructors B C D E G F

A Binært tre B D get. Root - get. Left - get. Right C E G F

A Binært tre B D attach. Left - attach. Right C E G F

A B Binært tre is. Empty - is. Leaf - remove. All C D E G F

A Binært tre B D dept. First. Traversal C E G F

A B Binært tre breadth. First. Traversal C D E G F

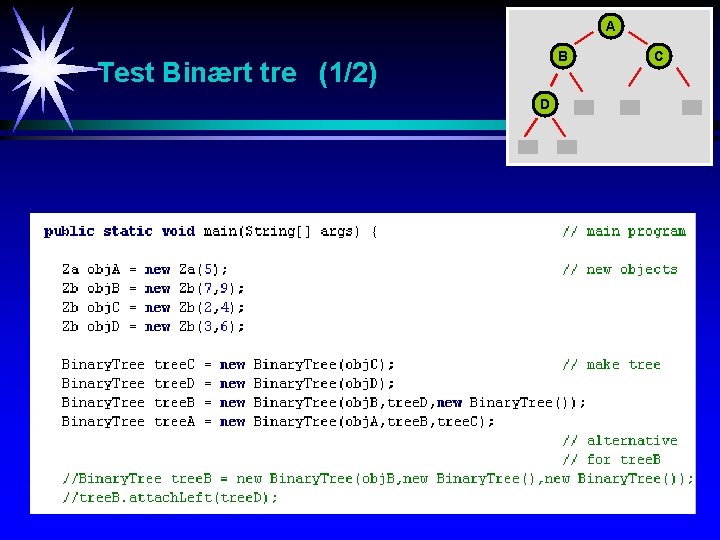
A B Test Binært tre (1/2) D C

A B Test Binært tre (2/2) D C

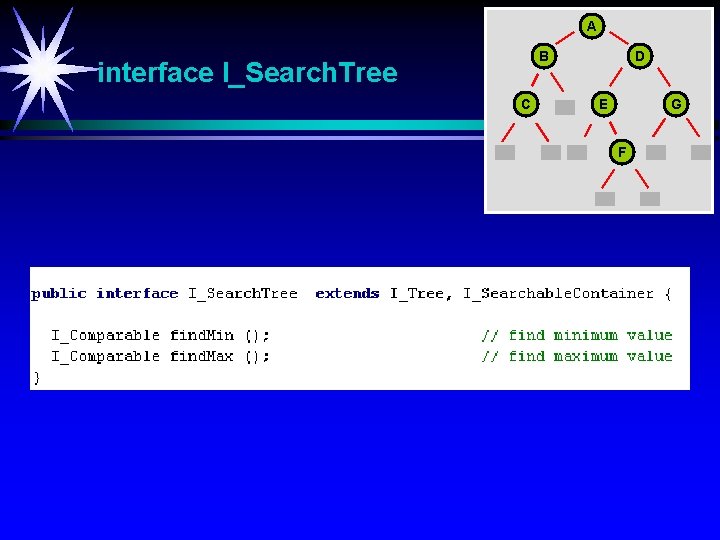
A B interface I_Search. Tree C D E G F

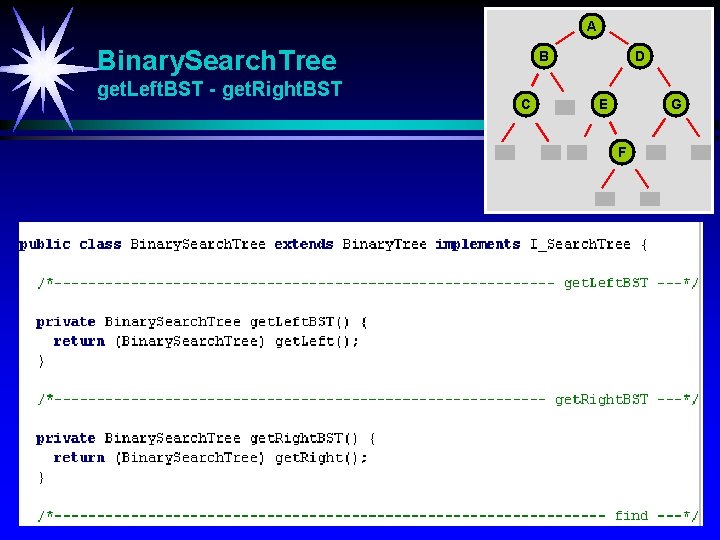
A Binary. Search. Tree get. Left. BST - get. Right. BST B C D E G F

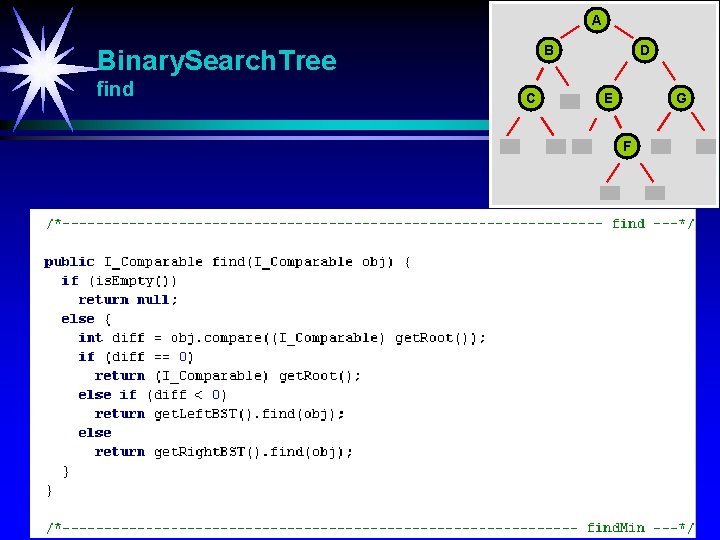
A B Binary. Search. Tree find C D E G F

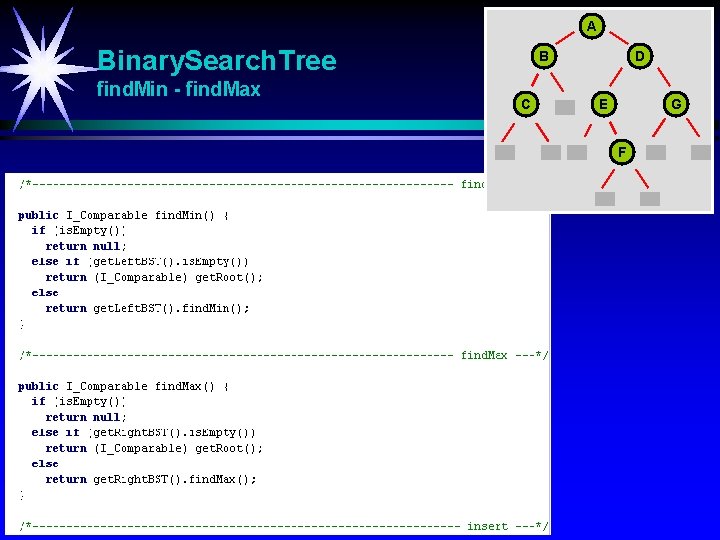
A Binary. Search. Tree find. Min - find. Max B C D E G F

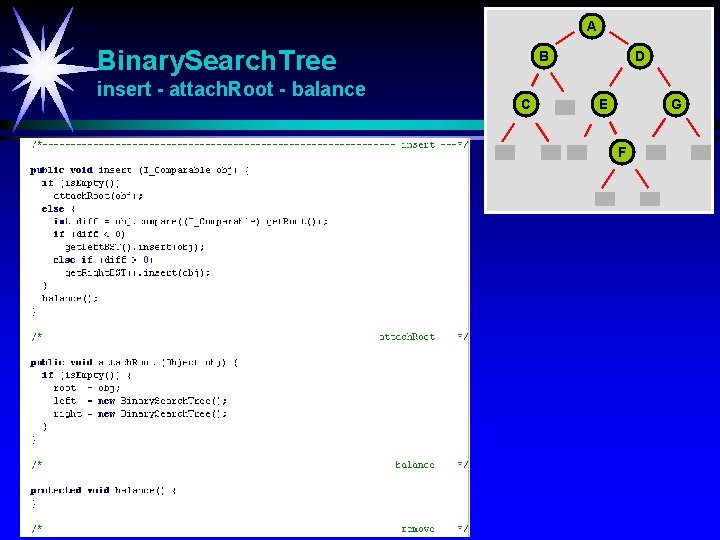
A Binary. Search. Tree insert - attach. Root - balance B C D E G F

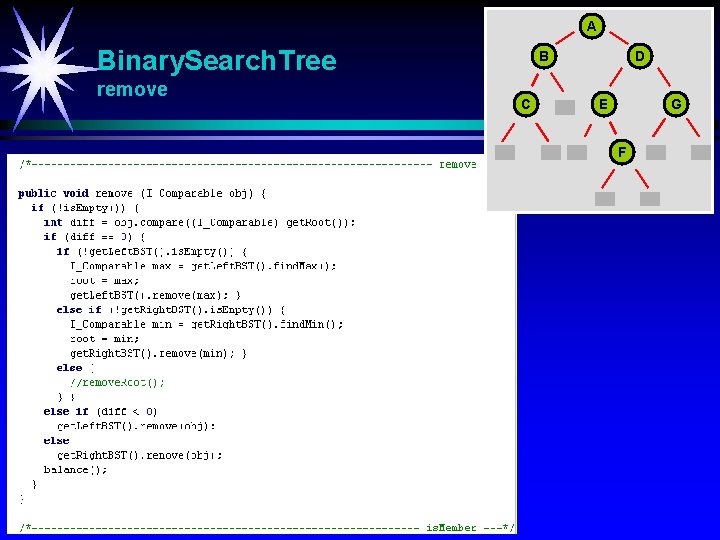
A Binary. Search. Tree remove B C D E G F

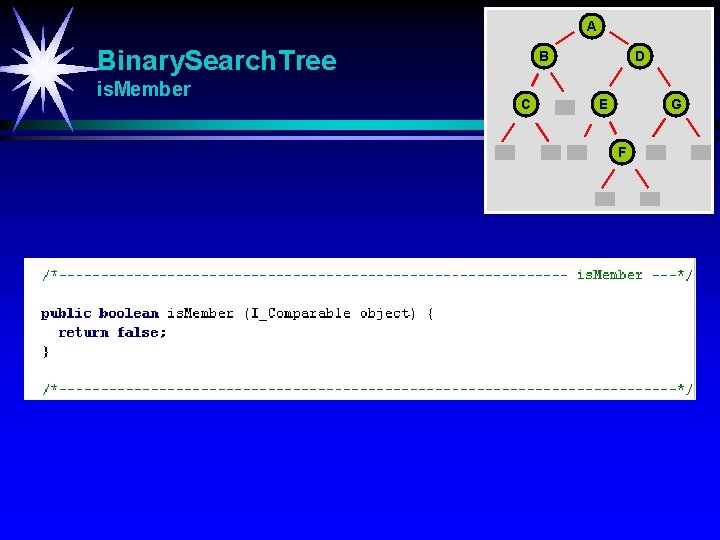
A Binary. Search. Tree is. Member B C D E G F

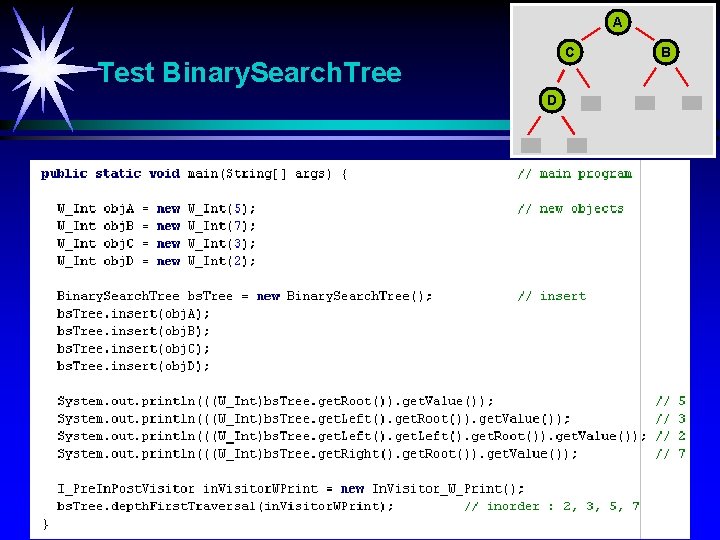
A C Test Binary. Search. Tree D B

END