K means clustering Step By Step Example Mr

K- means clustering Step By Step Example Mr. Balasaheb S. Tarle Associate Professor Computer Engineering MVP Samaj’s KBTCOE, Nasik

Typical Alternatives to Calculate the Distance between Clusters • Single link: smallest distance between an element in one cluster and an element in the other, i. e. , dis(Ki, Kj) = min(tip, tjq) • Complete link: largest distance between an element in one cluster and an element in the other, i. e. , dis(Ki, Kj) = max(tip, tjq) • Average: avg distance between an element in one cluster and an element in the other, i. e. , dis(Ki, Kj) = avg(tip, tjq) • Centroid: distance between the centroids of two clusters, i. e. , dis(Ki, Kj) = dis(Ci, Cj) • Medoid: distance between the medoids of two clusters, i. e. , dis(Ki, Kj) = dis(Mi, Mj) • Medoid: one chosen, centrally located object in the cluster 2

Centroid, Radius and Diameter of a Cluster (for numerical data sets) • Centroid: the “middle” of a cluster • Radius: square root of average distance from any point of the cluster to its centroid • Diameter: square root of average mean squared distance between all pairs of points in the cluster 3

Partitioning Algorithms Heuristic methods: k-means algorithm • K-means : Each cluster is represented by the center of the cluster • K-Means clustering intends to partition n objects into k clusters in which each object belongs to the cluster with the nearest mean. • This method produces exactly k different clusters of greatest possible distinction. • The best number of clusters k leading to the greatest separation (distance) is not known as a priori and must be computed from the data. • The objective of K-Means clustering is to minimize total intracluster variance, or, the squared error function: 4

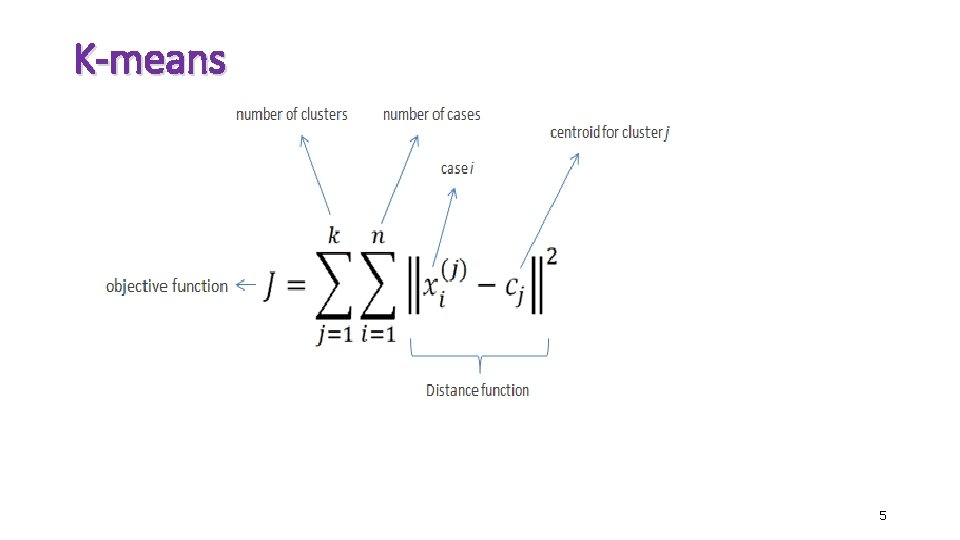
K-means 5

K-Means Algorithm 1. Clusters the data into k groups where k is predefined. 2. Select k points at random as cluster centers. 3. Assign objects to their closest cluster center according to the Euclidean distance function. 4. Calculate the centroid or mean of all objects in each cluster. 5. Repeat steps 2, 3 and 4 until the same points are assigned to each cluster in consecutive rounds. 6

The K-Means Clustering Method • Given k, the k-means algorithm is implemented in four steps: • Partition objects into k nonempty subsets • Compute seed points as the centroids of the clusters of the current partition (the centroid is the center, (i. e. , mean point, of the cluster) • Assign each object to the cluster with the nearest seed point • Go back to Step 2, stop when no more new assignment 7

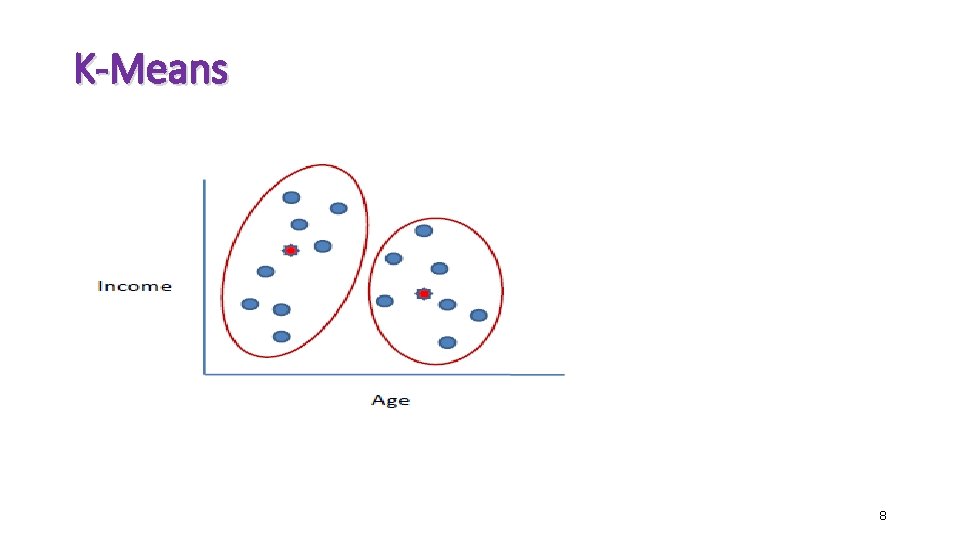
K-Means 8

K-Means • K-Means is relatively an efficient method. • We need to specify the number of clusters, in advance and the final results are sensitive to initialization and often terminates at a local optimum. • Unfortunately there is no global theoretical method to find the optimal number of clusters. • A practical approach is to compare the outcomes of multiple runs with different k and choose the best one based on a predefined criterion. • A large k probably decreases the error but increases the risk of overfitting. 9

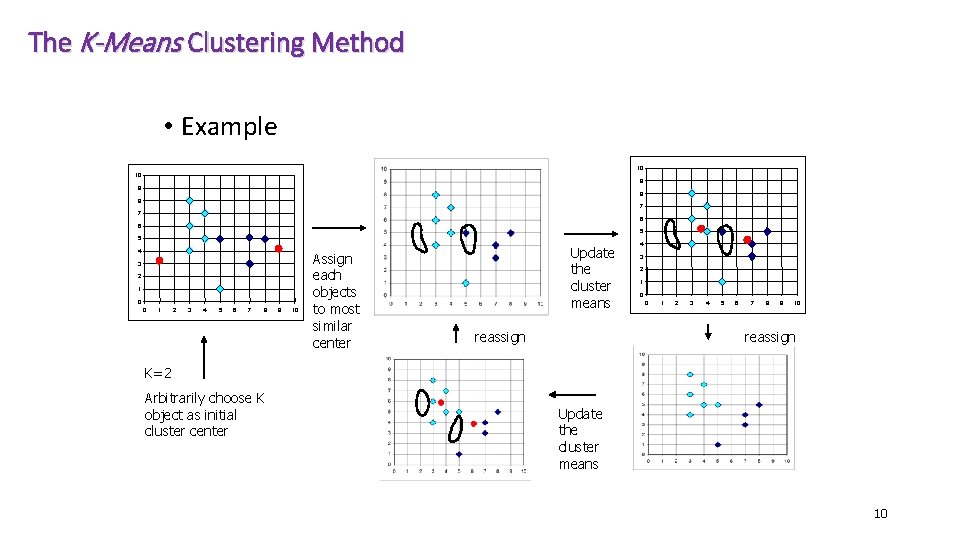
The K-Means Clustering Method • Example 10 10 9 9 8 8 7 7 6 6 5 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 Assign each objects to most similar center Update the cluster means reassign 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 reassign K=2 Arbitrarily choose K object as initial cluster center Update the cluster means 10

Example: Suppose we want to group the visitors to a website using just their age (a one-dimensional space) as follows: 15, 16, 19, 20, 21, 22, 28, 35, 40, 41, 42, 43, 44, 60, 61, 65 Initial clusters: Centroid (C 1) = 16 [16] Centroid (C 2) = 22 [22] Iteration 1: C 1 = 15. 33 [15, 16] C 2 = 36. 25 [19, 20, 21, 22, 28, 35, 40, 41, 42, 43, 44, 60, 61, 65] Iteration 2: C 1 = 18. 56 [15, 16, 19, 20, 21, 22] C 2 = 45. 90 [28, 35, 40, 41, 42, 43, 44, 60, 61, 65] 11

Example cont. • Iteration 3: • C 1 = 19. 50 [15, 16, 19, 20, 21, 22, 28] C 2 = 47. 89 [35, 40, 41, 42, 43, 44, 60, 61, 65] • Iteration 4: • C 1 = 19. 50 [15, 16, 19, 20, 21, 22, 28] C 2 = 47. 89 [35, 40, 41, 42, 43, 44, 60, 61, 65] • No change between iterations 3 and 4 has been noted. • By using clustering, 2 groups have been identified 15 -28 and 35 -65. • The initial choice of centroids can affect the output clusters, so the algorithm is often run multiple times with different starting conditions in order to get a fair view of what the clusters should be.

Example for Practice • Problem: Cluster the following eight points (with (x, y) representing locations) into three clusters A 1(2, 10) A 2(2, 5) A 3(8, 4) A 4(5, 8) A 5(7, 5) A 6(6, 4) A 7(1, 2) A 8(4, 9). Initial cluster centers are: A 1(2, 10), A 4(5, 8) and A 7(1, 2). The distance function between two points a=(x 1, y 1) and b=(x 2, y 2) is defined as: ρ(a, b) = |x 2 – x 1| + |y 2 – y 1|. • Use k-means algorithm to find the three cluster centers after the second iteration. 13

References • https: //www. analyticsvidhya. com/blog/2016/11/anintroduction-to-clustering-and-different-methods-ofclustering/ • https: //www. geeksforgeeks. org/clustering-in-machinelearning/