Junior Mathematics Trig Ratios Junior Mathematics Trig Ratios

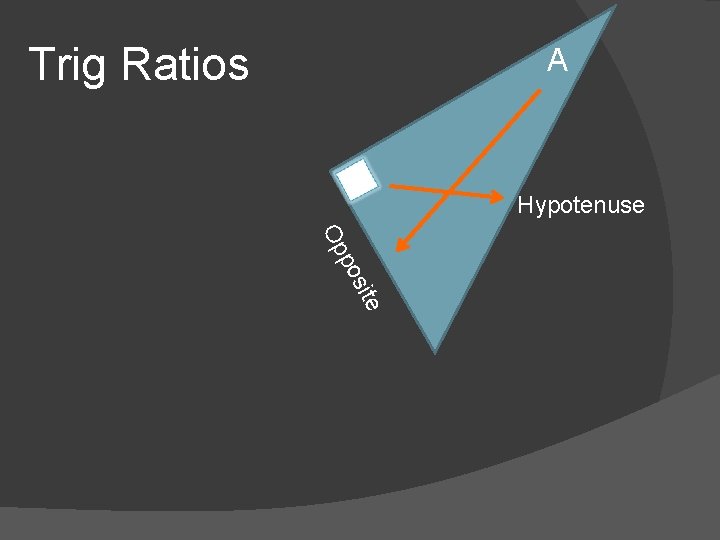
Junior Mathematics – Trig Ratios

Junior Mathematics – Trig Ratios !! r to la u lc a c y m n o s n h t g de i f n b … d n A o c e in t n in s u ix s e g i r T b o t t u

Here’s a happy student who nailed this topic!

Or , p er ha ps it’s SW EE TS !

YOU HAVE 3 SWEETS : ONE GREEN, ONE YELLOW, AND ONE RED. YOU ARE GOING TO PICK UP TWO PIECES ONE AT A TIME. THE QUESTION IS: IN HOW MANY DIFFERENT WAYS CAN YOU PICK UP TWO SWEETS? SHOW YOUR RESULTS IN A TABLE.

E. G

THERE ARE 6 COMBINATIONS

TRIGONOMETRIC RATIOS

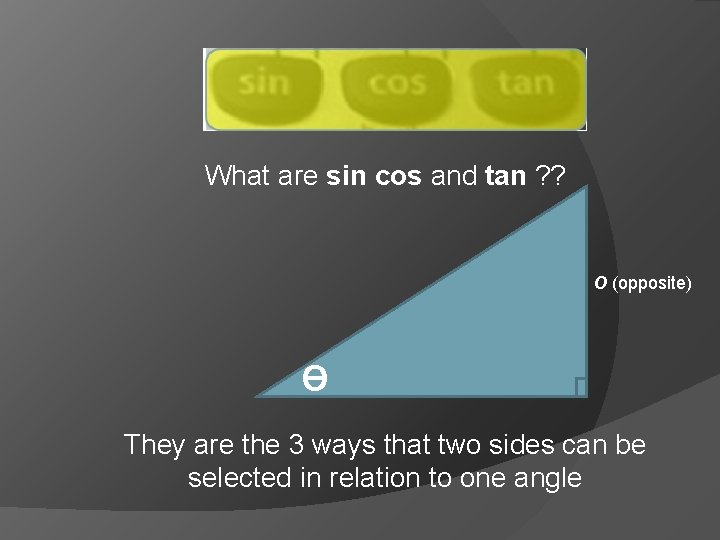
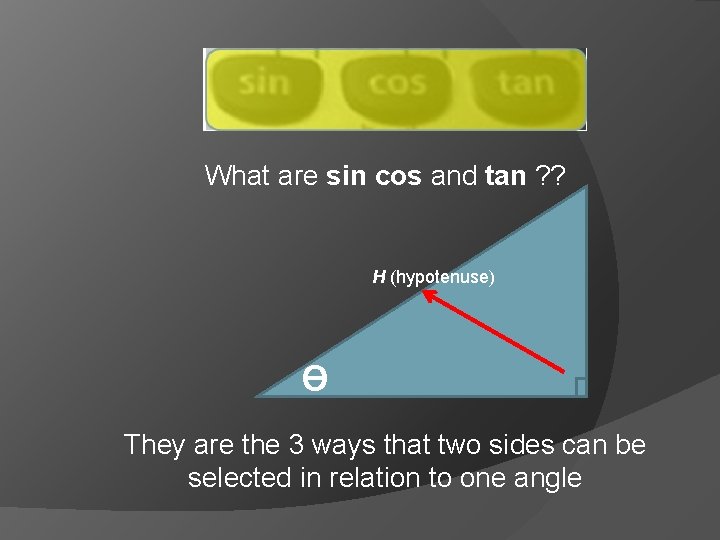
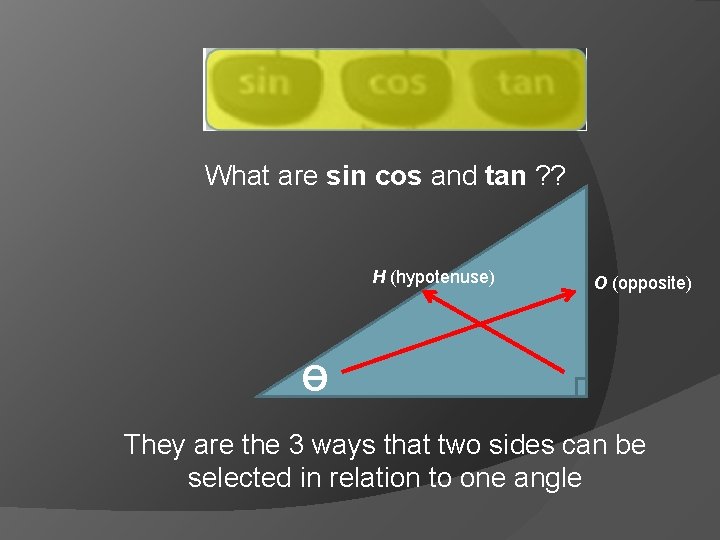
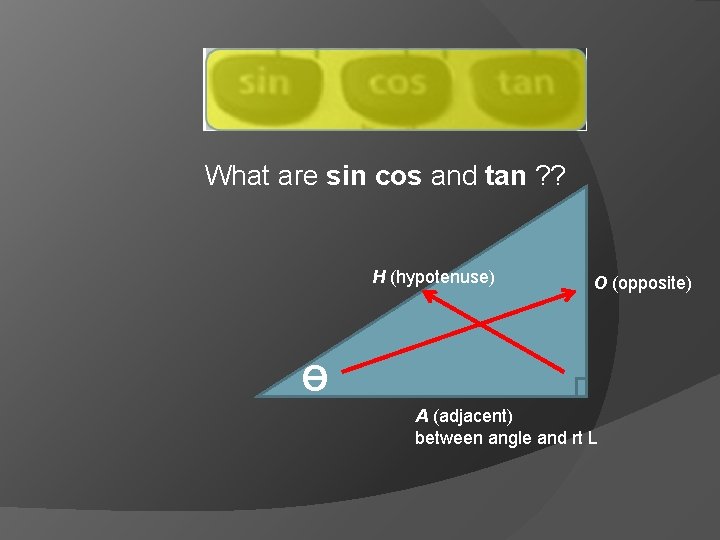
What are sin cos and tan ? ?

What are sin cos and tan ? ? Clues – used in Where there are 3 sides. So, like the sweets, we can combine two sides in 6 different ways

What are sin cos and tan ? ? Clues – used in They are the 3 ways that two sides can be selected in relation to one angle

What are sin cos and tan ? ? Ɵ They are the 3 ways that two sides can be selected in relation to one angle

What are sin cos and tan ? ? O (opposite) Ɵ They are the 3 ways that two sides can be selected in relation to one angle

What are sin cos and tan ? ? O (opposite) Ɵ They are the 3 ways that two sides can be selected in relation to one angle

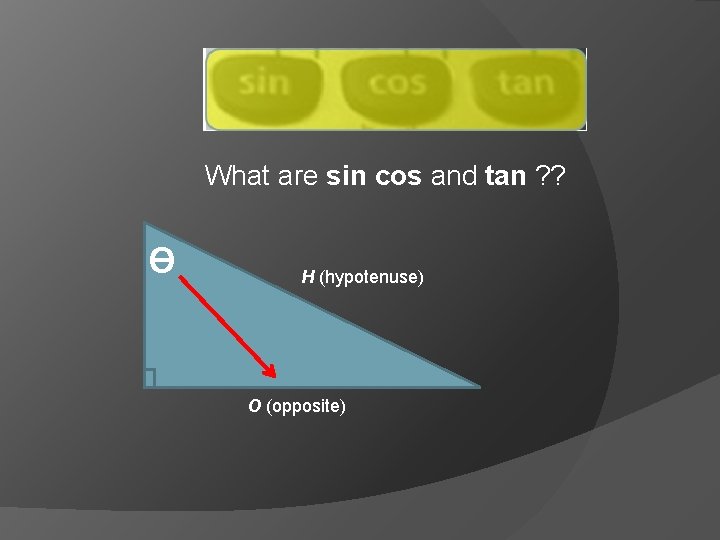
What are sin cos and tan ? ? H (hypotenuse) Ɵ They are the 3 ways that two sides can be selected in relation to one angle

What are sin cos and tan ? ? H (hypotenuse) O (opposite) Ɵ They are the 3 ways that two sides can be selected in relation to one angle

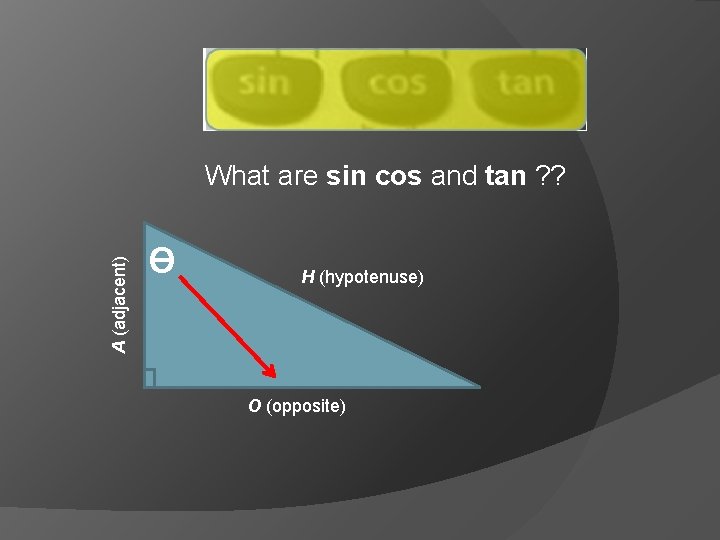
What are sin cos and tan ? ? H (hypotenuse) O (opposite) Ɵ A (adjacent) between angle and rt L

What are sin cos and tan ? ? Ɵ

What are sin cos and tan ? ? Ɵ H (hypotenuse)

What are sin cos and tan ? ? Ɵ H (hypotenuse) O (opposite)

A (adjacent) What are sin cos and tan ? ? Ɵ H (hypotenuse) O (opposite)

So, what are sin cos and tan ? ? They are the 3 ratios that two sides make in relation to one angle

-1 -1 -1 What are sin cos and tan ? Ɵ They are the 3 ways that an angle can be found when given the lengths of two sides

Finding Trig Ratios A trigonometric ratio is a ratio of the lengths of two sides of a right triangle. The word trigonometry is derived from the ancient Greek language and means measurement of triangles. The three basic trigonometric ratios are sine, cosine, and tangent, which are abbreviated as sin, cos, and tan respectively.

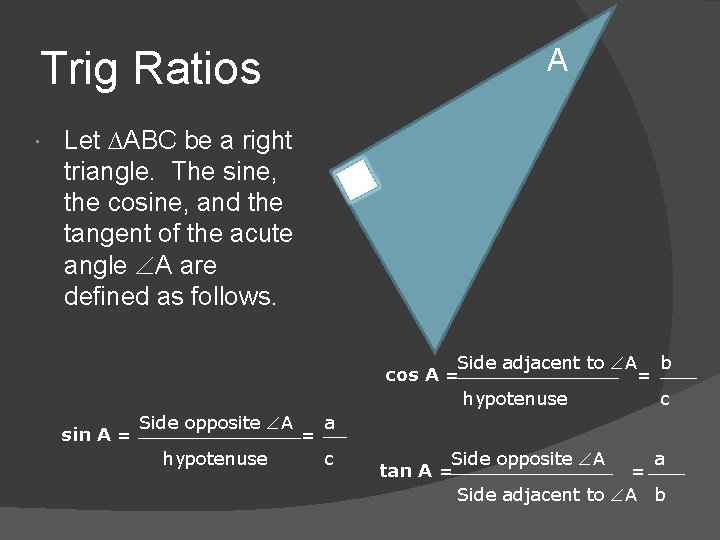
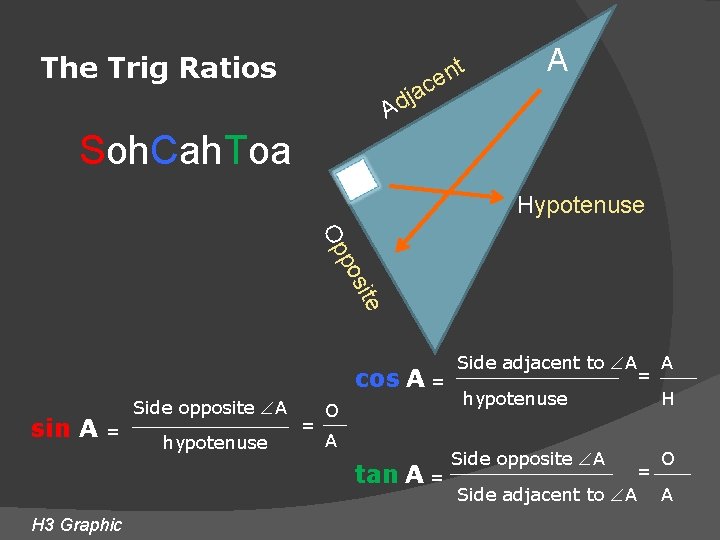
A Trig Ratios Let ∆ABC be a right triangle. The sine, the cosine, and the tangent of the acute angle A are defined as follows. Side adjacent to A b cos A = = hypotenuse c sin A = Side opposite A hypotenuse = a c Side opposite A a tan A = = Side adjacent to A b

Trig Ratios A Hypotenuse

Trig Ratios A Hypotenuse site po Op

The Trig Ratios A c a j d t en A Soh. Cah. Toa Hypotenuse Op site po cos A = sin A Side opposite A = hypotenuse = O A tan A = H 3 Graphic Side adjacent to A = hypotenuse Side opposite A Side adjacent to A A H = O A

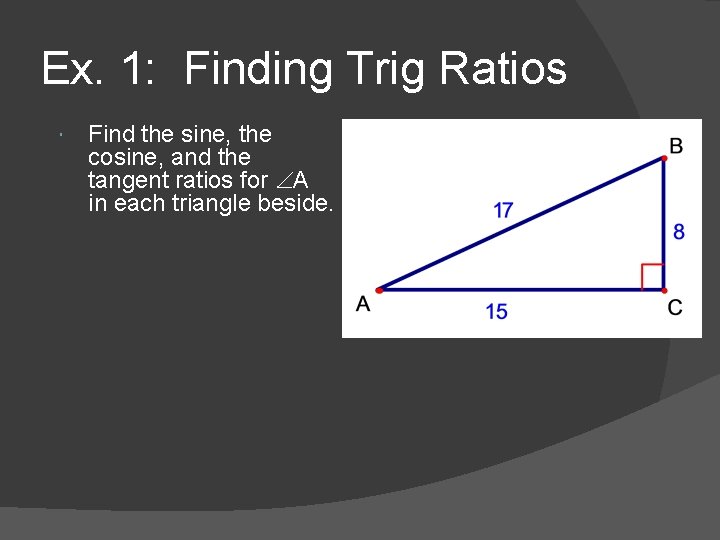
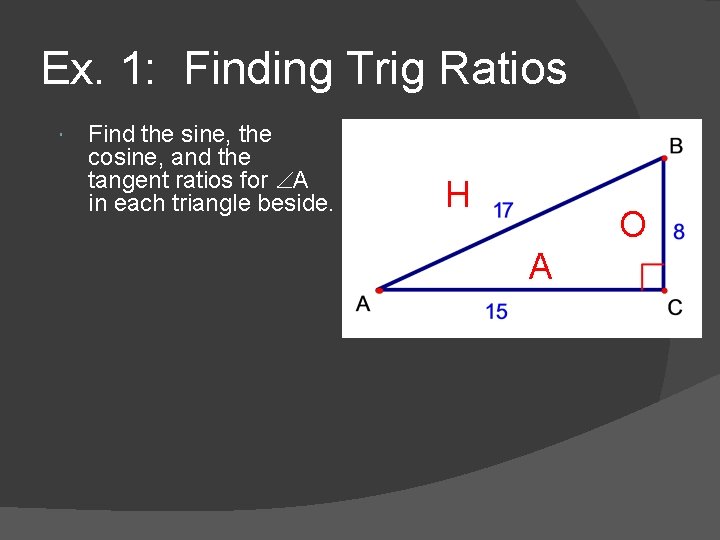
Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside.

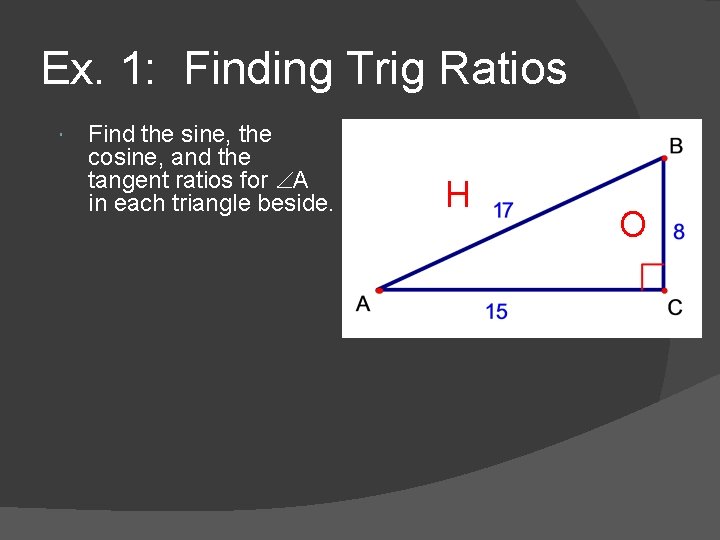
Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside. H O

Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside. H O A

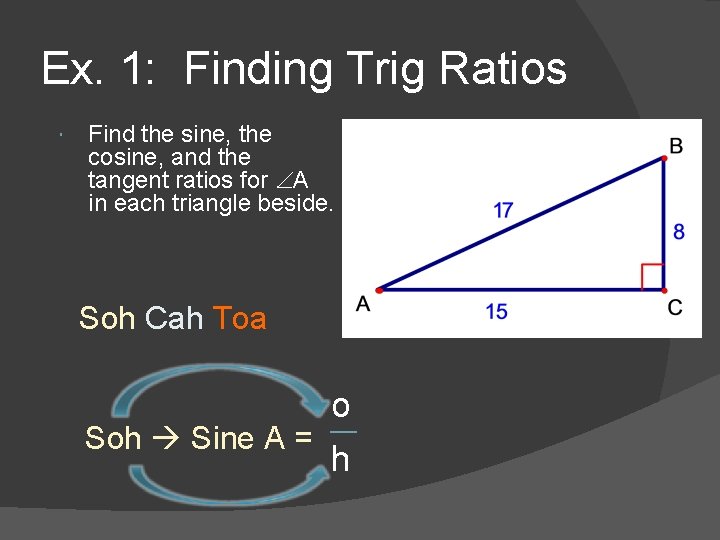
Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside. Soh Cah Toa o Soh Sine A = h

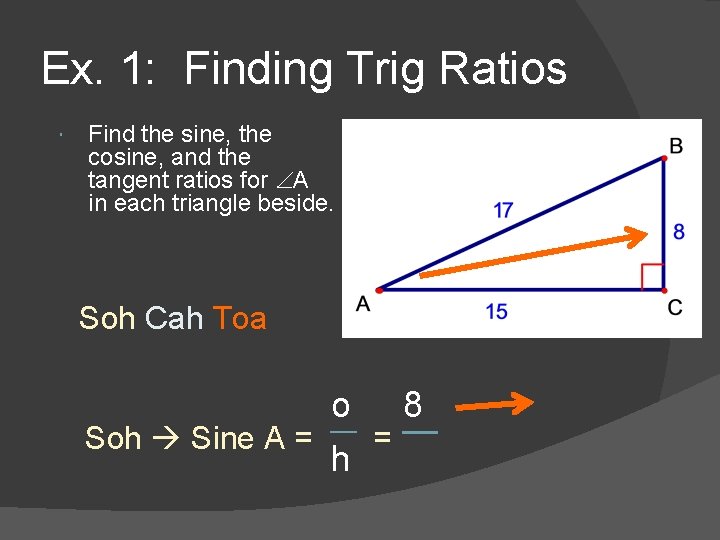
Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside. Soh Cah Toa o 8 Soh Sine A = = h

Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside. Soh Cah Toa o 8 Soh Sine A = = h 17

Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside. Soh Cah Toa o Soh Sine A = h

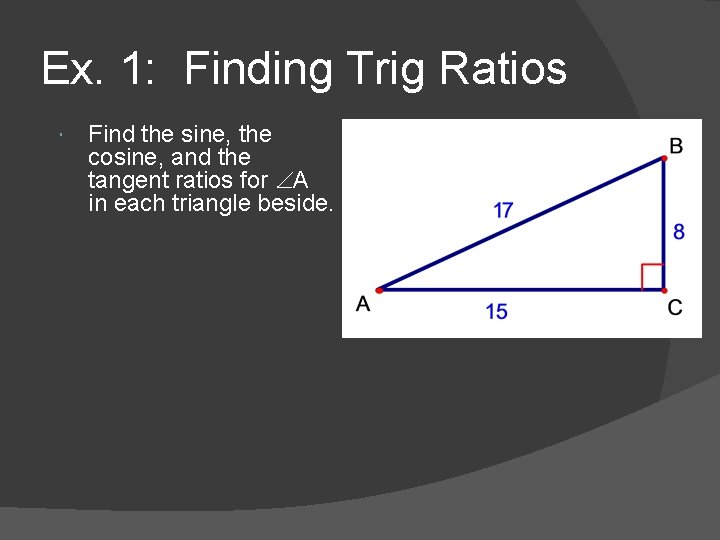
Ex. 1: Finding Trig Ratios Find the sine, the cosine, and the tangent ratios for A in each triangle beside.

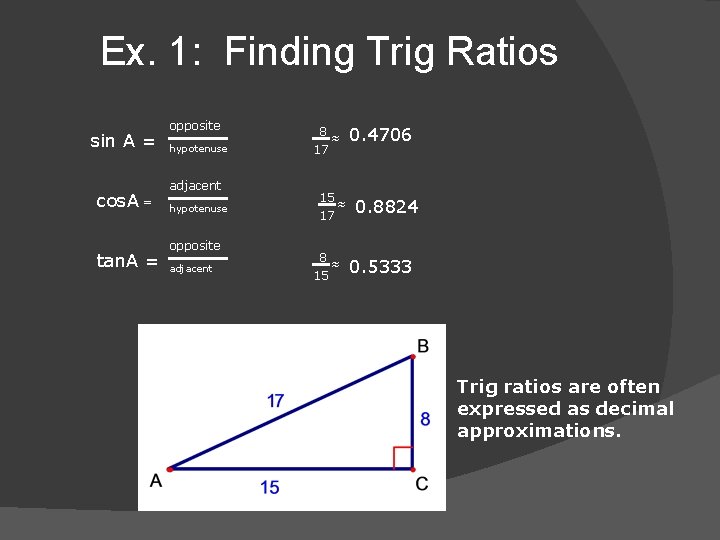
Ex. 1: Finding Trig Ratios sin A = cos. A = tan. A = opposite hypotenuse adjacent hypotenuse opposite adjacent 8 17 ≈ 15 ≈ 17 8≈ 15 0. 4706 0. 8824 0. 5333 Trig ratios are often expressed as decimal approximations.

Using a Calculator You can use a calculator to approximate the sine, cosine, and the tangent of 74. Make sure that your calculator is in degree mode. The table shows some sample keystroke sequences accepted by most calculators.

Ex 2 – sample keystrokes Sample keystroke sequences 74 SIN ENTER 74 COS ENTER 74 TAN ENTER Sample calculator display Rounded To 4 Decimal Places

Ex 2 – sample keystrokes Sample keystroke sequences SIN Sample calculator display Rounded To 4 Decimal Places 0. 961262695 0. 9613 0. 275637355 0. 2756 3. 487414444 3. 4874 74 ENTER 74 COS ENTER 74 TAN ENTER

Using Trigonometric Ratios in Reallife Suppose you stand look up at a point in the distance. Maybe you are looking up at the top of a tree as in Example 6. The angle that your line of sight makes with a line drawn horizontally is called angle of elevation.

Ex. 3: Indirect Measurement You are measuring the height of a pine tree in Alaska. You stand 15 m from the base of the tree. You measure the angle of elevation from a point on the ground to the top of the tree to be 59°. To estimate the height of the tree, you can write a trigonometric ratio that involves the height h and the known length of 15 m

The math tan 59° = opposite tan 59° = 15 tan 59° = h 15 (1. 6643) = h 24. 96 m = h Write the trig ratio adjacent h 15 Substitute values 15 Multiply each side by 15 Use a calculator to find tan 59° Simplify The tree is about 25 m tall

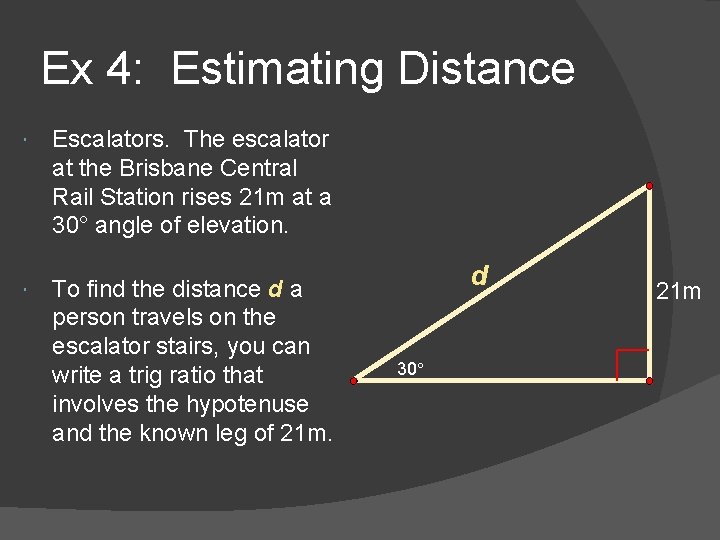
Ex 4: Estimating Distance Escalators. The escalator at the Brisbane Central Rail Station rises 21 m at a 30° angle of elevation. To find the distance d a person travels on the escalator stairs, you can write a trig ratio that involves the hypotenuse and the known leg of 21 m. d 30° 21 m

Now the maths sin 30° = opposite hypotenuse d d sin 30° = 21 d= for sine of 30° 21 sin 30° = d= Write the ratio 21 Substitute values. Multiply each side by d. Divide each side by sin 30° 21 0. 5 d = 42 m Substitute 0. 5 for sin 30° Simplify A person travels 42 m on the escalator stairs.

Using the inverse Trig ratios to find angles The angle that an anchor line makes with the sea bed is really critical for holding the ship. This angle depends upon the type of sea bed, etc. In this case, the sea bed is mud and the best angle for holding this ship is between 42 -50 degrees. Will the boat be safely anchored?

Using the inverse Trig ratios to find angles Soh. Cah. Toa The angle that an anchor line makes with the sea bed is really critical for holding the ship. This angle depends upon the type of sea bed, etc. In this case, the sea bed is mud and the best angle for holding this ship is between 42 -50 degrees. Will the boat be safely anchored?

Using the inverse Trig ratios to find angles Soh. Cah. Toa The angle at “a” uses the opposite side and the hypotenuse – that is, “o” and “h”. Therefore, the trig ratio must also use “o” and “h”, which is the Sine ratio. hypotenuse opposite The angle that an anchor line makes with the sea bed is really critical for holding the ship. This angle depends upon the type of sea bed, etc. In this case, the sea bed is mud and the best angle for holding this ship is between 42 -50 degrees. Will the boat be safely anchored?

Using the inverse Trig ratios to find angles Sin a° = opp hyp 18. 88 30 0. 8128 sin-1 x sin a° = sin-1 x 0. 8128 a anchor angle, a = Sin-1 (. 8128) = 54. 4 degrees (1 dp) No, the boat will not be safely anchored The angle that an anchor line makes with the sea bed is really critical for holding the ship. This angle depends upon the type of sea bed, etc. In this case, the sea bed is mud and the best angle for holding this ship is between 42 -50 degrees. Will the boat be safely anchored?