Jtkelmlet stratgiai magatarts Vlogatott fejezetek kzgazdasgtanbl Stratgiai magatarts

Játékelmélet, stratégiai magatartás Válogatott fejezetek közgazdaságtanból

Stratégiai magatartás • Amennyiben a piacon csak egy vállalat van, akkor a termelési mennyisége illetve árai meghatározásakor csak a saját költségeire, illetve a keresleti oldalra kell tekintettel lennie. • Ha pedig egy vállalat tökéletesen versenyző piacon működik, a piaci ár számára adottság lesz, így stratégia kialakítására ugyancsak nincs szükség. • Viszont akkor, ha egy vállalat nem árelfogadó, de nincs is egyedül a kínálati oldalon, döntenie kell arról is, hogy milyen módon viszonyul a piacon lévő többi vállalathoz, versenytársként vagy szövetségesként kezeli-e őket.

Játékelméleti megközelítés • A gazdasági szereplők stratégiai egymásra hatása nagyon változatos módokon történhet, és ezen interakciókat elvileg sokféle módon elemezhetnénk, de legcélszerűbb a játékelmélet eszköztárát segítségül hívnunk. • Az interakciót, a „játékot” egy ún. kifizetési mátrix segítségével írjuk le, és kétszemélyes, véges számú stratégiát tartalmazó játékokkal foglalkozunk.

Játéktípusok típusai • Az információs halmazok szerint: teljes információs játék ( inform. aszimmetria) • A játék egyfordulós vagy többször (véges vagy végtelen sokszor) ismétlik. • A szereplők egyszerre vagy egymás után döntenek (szimultán szekvenciális) • Kezdetben a legegyszerűbb, szimultán, teljes információs, egyfordulós játékokat elemezzük.

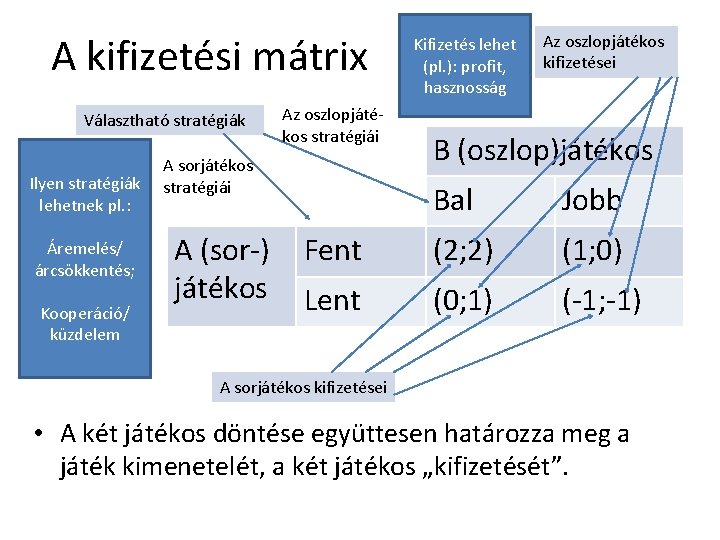
A kifizetési mátrix Választható stratégiák Ilyen stratégiák lehetnek pl. : Áremelés/ árcsökkentés; Kooperáció/ küzdelem Az oszlopjátékos stratégiái A sorjátékos stratégiái A (sor-) játékos Kifizetés lehet (pl. ): profit, hasznosság Az oszlopjátékos kifizetései B (oszlop)játékos Bal Jobb Fent (2; 2) (1; 0) Lent (0; 1) (-1; -1) A sorjátékos kifizetései • A két játékos döntése együttesen határozza meg a játék kimenetelét, a két játékos „kifizetését”.

Domináns stratégia • A játéknak létezik ún. domináns stratégián alapuló egyensúlya, ha mindkét játékos számára van olyan döntés, ami mindig optimális, attól függetlenül, hogy a másik játékos melyik lehetőséget választja. • Az előző példában pl. a „fent” az A játékos számára mindig magasabb kifizetést eredményez (2 > 1; 1 > -1); és a B játékos számára a „bal” mindig jobb, mint a „jobb” (2 > 1; 1 > -1). • A játék kimenetele tehát „fent, bal” lesz, a hozzá tartozó (2; 2) egységnyi kifizetéssel.

Nincs mindig domináns stratégia A: fent B: bal (1 > 0); de A: lent B: jobb (2 > 0); B: bal A: fent (2 > 0); de B: jobb A: lent (1 > 0). A (sor-) játékos B (oszlop)játékos Bal Jobb Fent (2; 1) (0; 0) Lent (0; 0) (1; 2) Domináns stratégián alapuló egyensúlya nem minden játéknak van, ebben a példában pl. ha az A játékos a „fentet” választja, a B játékos legjobb választása a „bal”, de ha a „jobbot”, akkor a lent. (A játék szimmetrikus. )

Nash-egyensúly Minden domináns stratégián alapuló egyensúly egyben Nash-egyensúly is. • Ilyen esetekben feltételeznünk kell azt, hogy a másik játékos racionálisan fog dönteni, és meg kell keresni azt, hogy a másik szereplő optimális választása esetén számunkra milyen választás lesz optimális. • Egy stratégiapáros [pl. fent, bal] ún. Nash-egyensúlyt alkot, ha B adott döntése esetén A döntése optimális, és A adott döntése esetén B döntése is optimális. • A Nash-egyensúly úgy értelmezhető, mint a másik játékos választására vonatkozó kölcsönös várakozás: a másik döntéséről tudomást szerezve senki sem akarja megváltoztatni a magatartását.

Egynél több Nash-egyensúly • Egy játéknak akár több Nash-egyensúlyi pontja is lehet, pl. ha az A játékos a „fentet” választotta, a B játékos a „balt”, akkor az a játékos csökkentené a kifizetését, aki megváltoztatná a döntést. • De amennyiben a B játékos a „jobb” stratégiát választotta, az A pedig a „lentet”, akkor innen sem éri meg egyik játékosnak sem elmozdulni.

Nincs „tiszta” Nash-egyensúly A: fent B: bal (0 > -1); de B: bal A: lent (1 > 0); ám A: lent B: jobb (3 > 0); viszont B: jobb A: fent (0 > -1) stb. A (sor-) játékos B (oszlop)játékos Bal Jobb Fent (0; 0) (0; -1) Lent (1; 0) (-1; 3) Van olyan játék is, amelynek ún. „tiszta stratégiák” esetén nincs Nash-egyensúlya, pl. a fenti játék esetében ha A fentet játszik, akkor B a balt választja; ekkor A inkább a lentet; de ilyenkor B a jobbra vált; amire A válasza a fent.

Tiszta és kevert stratégiák • Tiszta stratégiák: mindegyik szereplő meghozza a döntését, amihez aztán ragaszkodik. • Tiszta stratégiákra nem mindig létezik Nashegyensúly. Kevert stratégiákra azonban ilyenkor is létezhet. • Kevert stratégia: minden szereplő a stratégiákhoz adott p, q, … valószínűségeket rendel, és egyszer az egyik, másszor (gyakrabban vagy ritkábban – a választott valószínűségektől függően) a másik döntést hozza meg.

Kevert stratégia • A cél az, hogy a másik adott (optimális) stratégiája esetén a mi valószínűségekről hozott döntésünk optimális legyen. • A játékos r valószínűséggel a fentet, (1 -r) valószínűséggel a lentet választja. • B játékos c valószínűséggel a balt, (1 -c) valószínűséggel pedig a jobbot.

Kifizetések kevert stratégiáknál • Ekkor az egyes kifizetések, szorozva a valószínűségekkel: (0. rc; 0. rc) (1. [1 -r]c; 0. [1 -r]c) (0. r[1 -c]; -1. r[1 -c]) (-1. [1 -r][1 -c]; 3. [1 -r][1 -c]) • A játékosok várható kifizetései: • π(A) = 0 rc + 0 r[1 -c] + 1[1 -r]c − 1[1 -r][1 -c] = 1[1 -r]c − 1[1 -r][1 -c] • π(B) = 0 rc − 1 r[1 -c] + 0[1 -r]c + 3[1 -r][1 -c] = = 3[1 -r][1 -c] − 1 r[1 -c] =

A játékosok célfüggvényei • B játékosnál: • A függvények maximumhelye (a függvények parciális deriváltjai, azzal a feltételezéssel, hogy dr*/dc=0 és dc*/dr=0 ): Azaz az A játékos 75% valószínűséggel a fentet, 25% valószínűséggel a lentet fogja játszani, B pedig fele-fele arányban a balt és a jobbat.

Legjobbválasz-görbék • Az előző megoldás a lokális maximumpontot adta meg (a ]0; 1[ intervallumon belül), általánosságban azonban egy játéknak lehet több Nash-egyensúlyi pontja is; amelyek között köztes és szélső [tiszta stratégiákra is értelmezett] megoldások egyaránt lehetnek. • A tiszta és kevert stratégiákra értelmezett összes egyensúlyi pont meghatározásához az ún. legjobbválasz-görbéket használhatjuk fel.

Legjobb válaszok • Egy játékos „legjobb válasza” az a választás, amely a másik játékos tetszőleges választása esetén a kifizetését maximalizálja. • Ha nem egyetlen legjobb választása van, akkor a legjobb válasz valamennyi ilyen választás halmaza. Nézzük az alábbi, korábban már bemutatott játékot, aminek a tiszta stratégiák közt két egyensúlya volt: A (sor-) játékos B (oszlop)játékos Bal Jobb Fent (2; 1) (0; 0) Lent (0; 0) (1; 2)

Nash-egyensúly ált. definíciója • Tekintsünk egy kétszemélyes játékot, amelyben a sorjátékos lehetséges választásai r 1, …, r. R; az oszlopjátékosé pedig c 1, …, c. C • A sorjátékos minden r választásához tartozzon az oszlopjátékosnak egy bc(r) legjobb választása, és az oszlopjátékos minden c választásához a sorjátékosnak egy br(c) legjobb választása. • Ekkor a játék Nash-egyensúlya az az (r*, c*) stratégiapár lesz, amely kielégíti az alábbi egyenleteket:

Kölcsönös következetesség • A Nash-egyensúly definíciója azt követeli meg a választásoktól, hogy kölcsönösen következetesek legyenek. Ha a sorjátékos úgy véli, hogy az oszlopjátékos a balt választja, akkor a fentet fogja játszani, ha viszont az oszlopjátékos arra számít, hogy a sorjátékos a fentet választja, akkor a balt fogja játszani. • Vagyis a Nash-egyensúlyban a játékosok vélekedései és tényleges cselekedetei azok, amelyek kölcsönösen következetesek.

Az összes Nash-egyensúly • Mivel most már megoldásainkat (a Nash-egyensúlyt) nemcsak a tiszta, hanem a kevert stratégiák mellett is keressük; tegyük fel, hogy r annak a valószínűsége, hogy a sorjátékos a fentet választja, és (1 -r) a lent választás valószínűsége. • Hasonlóan, legyen c annak a valószínűsége, hogy az oszlopjátékos a balt, (1 -c), hogy a jobb stratégiát választja. • Tiszta stratégiák esetében r vagy c értéke 0 vagy 1.

Kevert stratégiák esetén (2; 1) (0; 0) (1; 2) • Számítsuk ki a játékosok várható kifizetéseit, ha a sorjátékos r valószínűséggel választja a fent, az oszlopjátékos pedig c valószínűséggel a bal stratégiát: Kombinációk Valószínűség A játékosok Várható kifizetések kifizetése Sorjátékos Oszlopjátékos (fent; bal) r. c (2; 1) 2 rc + (lent; bal) (1−r). c (0; 0) 0(1−r). c + (fent; jobb) r. (1−c) (0; 0) 0 r(1−c) + (lent; jobb) (1−r). (1−c) (1; 2) (1−r). (1−c) = 2(1−r). (1−c) = = 3 rc+1−r−c = 3 rc+2− 2 r− 2 c

A kifizetés változása ha r változik • Tfh. a sorjátékos azon gondolkodik, hogy a fent stratégia választásának r valószínűségét Δr-rel megnövelje. Hogyan változik a kifizetés? • π(A[r])= 3 rc − r − c + 1 • π(A[r+Δr]) − π(A[r]) = 3(r+Δr)c − (r+Δr) − c + 1 − − 3 rc + r + c − 1 = 3Δrc − Δr = (3 c − 1)Δr • E kifejezés értéke akkor pozitív, ha 3 c > 1 és negatív, ha 3 c < 1; azaz a sorjátékos akkor kívánja majd növelni r értékét, ha c > 1/3 és csökkenteni, ha c < 1/3; illetve bármilyen 0 és 1 közötti valószínűséggel elégedett, ha c = 1/3

A kifizetés változása ha c változik • Tfh. az oszlopjátékos azon gondolkodik, hogy a bal stratégia választásának c valószínűségét Δcvel megnövelje. Hogyan változik a kifizetés? • π(B[c])= 3 rc − 2 r − 2 c + 2 • π(B[c+Δc]) − π(B[c]) = 3(c+Δc)r − 2(c+Δc) − 2 r + 2 − − 3 rc + 2 r − 2 = 3Δrc − 2Δc = (3 r − 2)Δc • E kifejezés értéke akkor pozitív, ha 3 r > 2 és negatív, ha 3 r < 2; azaz az oszlopjátékos akkor kívánja majd növelni c értékét, ha r > 2/3 és csökkenteni, ha r < 2/3; illetve bármilyen 0 és 1 közötti valószínűséggel elégedett, ha r = 2/3

A legjobbválasz-görbék • Ezeket az információkat felhasználva megrajzolhatók a legjobbválasz-görbék. • Ha az oszlopjátékos c = 0 -t választ, akkor a sorjátékos az r értékét a lehető legkisebb értéken szeretné meghatározni, ami r = 0. • Ez a választás nem változik, amíg c < 1/3, ha viszont c = 1/3, akkor bármely r∈(0; 1) legjobb válasznak minősül. Ha c > 1/3, akkor a sorjátékos legjobb válasza r = 1.

Legjobbválaszgörbe c Hasonlóan, amíg r < 2/3, addig c=0; ha r > 2/3, akkor c=1 a legjobb válasz, ill. ha r = 2/3, akkor c 0 és 1 között bármennyi lehet. A három Nash-egyensúly a metszéspontokban található: (0; 0), (1; 1) és (2/3; 1/3). A sorjátékos legjobb választása 0 Az oszlopjátékos legjobb választása r

A Nash-egyensúly és a Pareto-hatékonyság • A tökéletes verseny esetében „jól működött” az ún. „láthatatlan kéz”, azaz az egyes szereplők optimális döntései egyben a társadalom számára is optimális (ún. Pareto-hatékony) eredményre vezettek. • A Nash-egyensúly esetében viszont ez nem feltétlenül teljesül, tehát elképzelhető, hogy bár mindkét fél a maga számára optimális döntést hoz, a végső kifizetés egy másik döntés esetén mindkettejük számára magasabb lehetett volna.

Fogolydilemma • Alapszituáció: Két előzetesben lévő gyanúsítottat külön hallgatnak ki. Mindketten dönthetnek, hogy vallomást tesznek-e a másikra vagy tagadják a bűntény elkövetését. • Ha csak egyikük vall, őt elengedik, és a másik 6 hónap büntetést kap; ha mindkettejük, akkor pedig 3 -3 hónapot. Ha mindketten tagadnak, akkor egy kisebb bűncselekmény alapján 1 -1 hónap büntetést kapnak.

A fogolydilemma kifizetési mátrixa Ha mindketten biztosak lehetnének abban, hogy a másik nem fog „köpni”, akkor kisebb büntetéssel is megúszhatnák. 2. gyanusított A kifizetések a börtönben töltendő hónapok -1*-esei Vall Tagad 1. gyanú- Vall sított Tagad (-3; -3) (0; -6) (-6; 0) (-1; -1) Mindkét játékos számára a vallomástétel lesz a domináns stratégia [(-3 > -6) és (0 > -1)], így a (vall; vall) kimenet lesz a domináns stratégián alapuló egyensúly, de ez nem Paretohatékony.

A fogolydilemma-játék közgazdasági alkalmazásai • Ez a gondolatmenet alkalmazható arra az esetre, ha egy duopolista iparágban a vállalatok kartellbe tömörülnek, azaz nem egymással versengve a saját, hanem az együttes profitjukat próbálják maximalizálni. • Ilyenkor az optimális kimenet érdekében mindkettejüknek a „monopolista” árhoz kellene tartaniuk magukat, de az egyéni profitjukat növelhetnék, ha a megállapodást megszegve árat csökkentenének.

Ismételt játékok • A játék kimenete különbözhet akkor, ha a játékot nem csak egyszer játszanák le, hanem a szereplők többször kerülnének ugyanabba a helyzetbe. • Az előző példában például, ha a vállalat tudja, hogy a kartell-megállapodás megszegéséért a versenytársa „meg tudja büntetni őt”, azzal hogy csökkenti az árait, akkor ez kevésbé kifizetődővé tehetné számára a csalást.

Véges sokszor ismételt játék • Ha a játékot csupán véges számban ismétlik meg, és mindketten tudják, hogy melyik lesz az utolsó forduló, akkor ebben a fordulóban úgy kell viselkedniük, mintha a játékot csak egyszer játszanák le, azaz pl. mindketten cserbenhagyják a másikat. • Ha viszont tudják, hogy a másik az utolsó alkalommal cserben fogja őket hagyni, akkor már az utolsó előtti alkalommal sem kell kalkulálniuk azzal, hogy legközelebb a társuk bosszúból nem fog kooperálni, mert tudják, hogy ez úgyis mindenképpen bekövetkezik, így az utolsó előtti fordulóban is csalnak. • Ezt a gondolatmenetet kiterjesztve pedig már az első fordulóban is mindketten csalni fognak.

Végtelen sokszor ismételt játék • Ha azonban a játék végtelen sokszor ismétlődhet, akkor van mód az ellenfél magatartásának befolyásolására. • Ilyenkor a döntésünket attól is függővé tehetjük, hogy a másik az előző forduló(k)ban mit lépett; és a nemkooperatív magatartását „megbüntethetjük”, rákényszerítve a kooperálásra. • Míg az egyszer lejátszott, és a véges számban ismételt fogoly-dilemma típusú játék esetében mindig a „vallomástétel” a nyerő stratégia, a végtelen sokszor ismételt játékban sikeresebbek lehetnek az eleinte együttműködő, de a másik cserbenhagyását a következő fordulóban megbosszuló „szemet-szemért stratégiák” (tit for tat; tit for two tats).

Szekvenciális játékok • A játékosok gyakran nem egy időben, hanem egymás után hozzák meg a döntéseiket, pl. A játékos először dönt arról, hogy a fent vagy a lent opciót válassza, és B csak ezután dönti el, hogy a bal vagy a jobb opciót válassza. • Ekkor a kifizetési mátrix helyett a játékot ún. extenzív formában (döntési fával) ábrázoljuk, ami a választás időbeliségét is tükrözi.

Szekvenciális játék „kifizetési mátrixa” A kifizetési mátrix elrejti a tényt, hogy az egyik játékos tudni fogja, hogy a másik mit választott az ő döntése előtt; nem érzékelteti a játék aszimmetrikus természetét. A (sor-) játékos B (oszlop)játékos Bal Jobb Fent (1; 9) Lent (0; 0) (2; 1) A fenti játékban pl. két Nash-egyensúlyi pont is van, a (fent; bal) és a (lent; jobb), de ha B csak A után hozza meg a döntését, akkor ezek közül csak az egyik valósulhat meg.

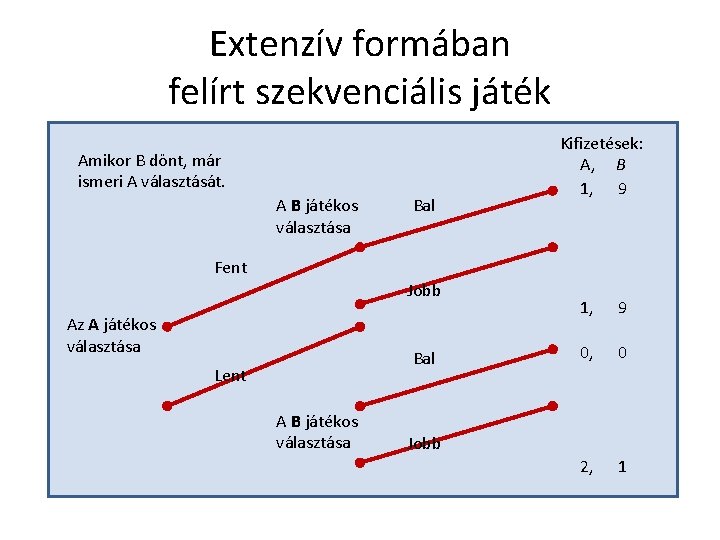
Extenzív formában felírt szekvenciális játék Amikor B dönt, már ismeri A választását. A B játékos választása Bal Kifizetések: A, B 1, 9 Fent Jobb Az A játékos választása Bal Lent A B játékos választása 1, 9 0, 0 2, 1 Jobb

A játék megoldása • Ha az A játékos már meghozta a döntését, és a fentet választotta, akkor B bármit választ, a játék kifizetése (1; 9) lesz. • Ha viszont A a lentet választja, akkor B számára célszerű a jobbot választani (1 > 0), így a játék kifizetése (2; 1) lesz. • Így, amikor A kezdetben dönt, akkor már figyelembe veheti B várható reakcióját, és a fent döntés 1; a lent döntés (a várható „jobb” döntés esetén) 2 hasznosságot jelent számára. • A így a lentet, B a jobbot fogja választani.

A végkimenetel B szempontjából • A (fent; bal) stratégiapáros szekvenciális játék esetében nem egyensúlyi pont, csak a (lent; jobb) az. • B játékos ezzel rosszul jár, hiszen mindenképpen az 1 kifizetéssel kell megelégednie a (fent; bal) esetén várható 9 helyett, de nem tud ez ellen mit tenni, hiszen ha A már meghozta a döntését (lent), számára a „jobb” az egyetlen racionális választás. • Ha B játékos el tudná hitetni A-val, hogy mindenképpen a balt fogja választani, akkor jobb helyzetbe kerülhetne, de ehhez (előre) szűkítenie kell a döntési lehetőségeit.

Zéró összegű játékok • A játékok egy része esetében a két játékos mindenképpen verseng egymással, mert csak egymás rovására érhetnek el magasabb kifizetéseket. • A zéró összegű játékokban az egyik játékos pozitív kifizetése (nyeresége) egyenlő a másik játékos negatív kifizetésével (veszteségével). • Pl. a labdajátékok (sport) általában tipikusan ebbe a kategóriába tartoznak (az egyik által elért gól/pont miatt a másik távolabb kerül a győzelemtől).

Példa a zéró összegű játékokra (Büntetők egy futballmeccsen) • A sorjátékos (csatár) büntetőt rúg, az oszlopjátékos (kapus) szeretné hárítani. • A sorjátékos a büntetőt rúghatja jobbra vagy balra, az oszlopjátékos pedig vetődhet jobbra vagy balra. A két játékos szimultán dönt arról, hogy merre rúgja a labdát ill. merre vetődjön. • A játék kifizetéseit a sikeres büntetők százalékában fejezhetjük ki. A játék nem feltétlenül szimmetrikus, hiszen a rúgó lehet jobb- vagy ballábas, a kapus jobb- vagy balkezes.

A büntető-játék kifizetési mátrixa Jobbkezes kapus, jobblábas rúgó: a kifizetések azt mutatják, hogy az esetek hány százalékában sikeres a büntető, ha a sorjátékos az adott irányba rúgja és az oszlopjátékos az adott irányba vetődik. A (sor-) játékos A kapus ugyanannyira örül annak is, ha a csatár mellérúgja, mintha ő védené ki! B (oszlop)játékos Bal Jobb Bal (50; -50) (80; -80) Jobb (90; -90) (20; -20) A kifizetések összege mindegyik négyzetben nulla, a sorjátékos maximalizálni szeretné a sikeres 11 -es gyakoriságát, az oszlopjátékos ugyanakkor ezt minimalizálni (a saját negatív kifizetéseit maximalizálni) szeretné.

Kevert stratégiák • Ha bármelyik játékos előre tudná, hogy a másik merre rúgná a labdát, ill. merre vetődne, akkor előnybe kerülne. Így a sorjátékos időnként balra (p arányban), máskor az erősebbik oldalára (1 -p arányban) rúgja a büntetőt, az oszlopjátékos pedig hol balra (q arányban), hol jobbra (1 -q arányban) vetődik. • Azaz mindkét játékos kevert stratégiát fog követni. ( minimax-stratégia)

A sorjátékos A kifizetésének alakulása különböző p értékek mellett: 50 p + 90(1 -p) illetve 80 p + 20(1 -p) A (sor-) Bal játékos Jobb választása sorjátékos kifizetései B (oszlop)játékos választása Bal Jobb 50 p 80 p 90(1−p) 20(1−p) A sorjátékos felismeri, hogy az oszlopjátékos mindig minimalizálni akarja az ő várható kifizetéseit. Így bármilyen p választása mellett a legjobb kifizetés, amiben reménykedhet, a két stratégiából adódó lehetséges kifizetések minimuma: π = min{50 p + 90(1−p); 80 p + 20(1 − p)}

A sorjátékos stratégiája • A sorjátékos célja természetesen az, hogy ezt a kifejezést maximalizálja: • Mivel (90 − 40 p) értéke p=0 -nál 90, de p növekedésével csökken, és (60 p + 20) értéke p=0 -nál 20, de p növekedésével nő (p=1 -nél 80), így a kifejezés ott lesz maximális, ahol fennáll:

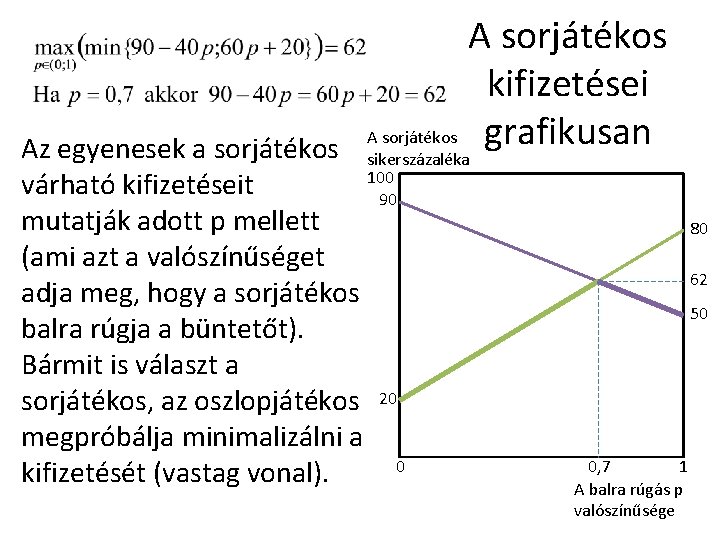
A sorjátékos kifizetései A sorjátékos grafikusan Az egyenesek a sorjátékos sikerszázaléka 100 várható kifizetéseit 90 mutatják adott p mellett (ami azt a valószínűséget adja meg, hogy a sorjátékos balra rúgja a büntetőt). Bármit is választ a sorjátékos, az oszlopjátékos 20 megpróbálja minimalizálni a 0 kifizetését (vastag vonal). 80 62 50 0, 7 1 A balra rúgás p valószínűsége

Az oszlopjátékos stratégiája A táblázat a sorjátékos kifizetéseit mutatja az oszlopjátékos adott q választása mellett; az oszlopjátékos kifizetése ennek -1*-ese. A (sor-) Bal játékos Jobb választása B (oszlop)játékos választása Bal Jobb 50 q 80(1−q) 90 q 20(1−q) • Az oszlopjátékos célja a sorjátékoséval éppen ellentétes, ő az alábbi kifizetést minimalizálná:

Az egyenesek a sorjátékos várható kifizetéseit mutatják adott q mellett (ami azt a valószínűséget adja meg, hogy a kapus balra fog elvetődni). Bármit is választ az oszlopjátékos, a sorjátékos megpróbálja maximalizálni a kifizetését (vastag vonal). A sorjátékos sikerszázaléka 100 A kapus stratégiája grafikusan 80 80 62 50 20 0 0, 6 1 A balra vetődés q valószínűsége

Az egyensúlyi stratégiák • Ezzel megadtuk az egyensúlyi stratégiákat mindkét játékos számára. A csatárnak az esetek 70%-ában balra kell rúgnia a labdát, a kapusnak 60%-ban balra kell vetődnie. • Ezeket az értékeket úgy választottuk meg, hogy a játékosok kifizetései ugyanazok legyenek, bármit is csinál a másik játékos, mivel ezeket a kifizetéseket a szemben álló játékosok stratégiai választásait egyenlővé téve kaptuk meg.

Az eredmények konzisztenciája • Ha a sorjátékos a p=0, 7 -es valószínűséget választja, az oszlopjátékos számára közömbös, hogy balra vagy jobbra vetődik. Az oszlopjátékos akkor lesz a legelégedettebb, ha q=0, 6 valószínűséggel vetődik balra. • Hasonlóan, ha az oszlopjátékos 0, 6 valószínűséggel balra vetődik, akkor a sorjátékos számára közömbös, hogy balra vagy jobbra rúgja a büntetőt. Az teszi leginkább elégedetté, ha balra rúg 0, 7 valószínűséggel.

Az egyensúly értelmezése • Ez azt jelenti, hogy ezek a valószínűségi választások egyben Nash-egyensúlyi helyzetek is: mindegyik játékos optimalizálja a helyzetét a másik adott választásai mellett. • Egyensúlyi helyzetben a sorjátékos 62 %-ban értékesíti a büntetőt, míg 38 %-ban kihagyja. Ez a legtöbb, amit elérhet, ha a másik játékos optimálisan válaszol. Hasonlóképpen, a kapus legfeljebb 38%-ban tudja elkerülni a gólt.

Legjobbválasz-görbék • Mi a helyzet akkor, ha a másik nem optimálisan válaszol? E kérdés megválaszolásához felhasználhatjuk a korábban már bemutatott legjobbválasz-görbéket. • Ha p kisebb 0, 7 -nél, akkor az oszlopjátékosnak balra kell vetődnie, ha nagyobb, akkor pedig jobbra. Hasonlóan, ha q kisebb 0, 6 -nál, a sorjátékosnak balra érdemes rúgni a büntetőt, ha nagyobb 0, 6 -nál, akkor pedig jobbra.

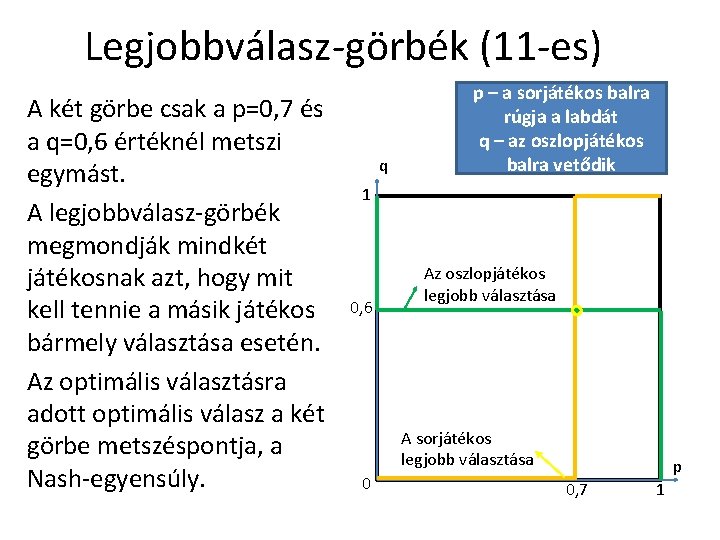
Legjobbválasz-görbék (11 -es) A két görbe csak a p=0, 7 és a q=0, 6 értéknél metszi egymást. A legjobbválasz-görbék megmondják mindkét játékosnak azt, hogy mit kell tennie a másik játékos bármely választása esetén. Az optimális választásra adott optimális válasz a két görbe metszéspontja, a Nash-egyensúly. q p – a sorjátékos balra rúgja a labdát q – az oszlopjátékos balra vetődik 1 0, 6 Az oszlopjátékos legjobb választása A sorjátékos legjobb választása 0 p 0, 7 1