JPEG Tutorial JPEG is the image compression standard

JPEG Tutorial JPEG is the image compression standard developed by the Joint Photographic Experts Group. It works best on natural images (scenes). This tutorial describes general JPEG compression for greyscale images. JPEG, unlike other formats like PPM, PGM, and GIF, is a lossy compression technique; this means visual information is lost permanently. The key to making JPEG work is choosing what data to throw away. Author: Ray Wolfgang

How JPEG Works JPEG divides up the image into 8 by 8 pixel blocks, and then calculates the discrete cosine transform (DCT) of each block. A quantizer rounds off the DCT coefficients according to the quantization matrix. This step produces the "lossy" nature of JPEG, but allows for large compression ratios. JPEG's compression technique uses a variable length code on these coefficients, and then writes the compressed data stream to an output file (*. jpg). For decompression, JPEG recovers the quantized DCT coefficients from the compressed data stream, takes the inverse transforms and displays the image.

The Discrete Cosine Transform The discrete cosine transform (DCT) helps separate the image into parts (or spectral sub -bands) of differing importance (with respect to the image's visual quality). The DCT is similar to the discrete Fourier transform: it transforms a signal or image from the spatial domain to the frequency domain. With an input image, A, the coefficients for the output "image, " B, are: The input image is N 2 pixels wide by N 1 pixels high; A(i, j) is the intensity of the pixel in row i and column j; B(k 1, k 2) is the DCT coefficient in row k 1 and column k 2 of the DCT matrix. All DCT multiplications are real. This lowers the number of required multiplications, as compared to the discrete Fourier transform. The DCT input is an 8 by 8 array of integers. This array contains each pixel's gray scale level; 8 bit pixels have levels from 0 to 255. The output array of DCT coefficients contains integers; these can range from -1024 to 1023. For most images, much of the signal energy lies at low frequencies; these appear in the upper left corner of the DCT. The lower right values represent higher frequencies, and are often small - small enough to be neglected with little visible distortion.

JPEG’s Quantizing Scheme There is a tradeoff between image quality and degree of quantization. A large quantization step size can produce unacceptably large image distortion. This effect is similar to quantizing Fourier series coefficients too coarsely; large distortion would result. Unfortunately, finer quantization leads to lower compression ratios. The question is how to quantize the DCT coefficients most efficiently. Because of human eyesight's natural high frequency roll-off, these frequencies play a less important role than low frequencies. This lets JPEG use a much higher step size for the high frequency coefficients, with little noticeable image deterioration.

Quantization Matrix The quantization matrix is the 8 by 8 matrix of step sizes (sometimes called quantums) - one element for each DCT coefficient. It is usually symmetric. Step sizes will be small in the upper left (low frequencies), and large in the upper right (high frequencies); a step size of 1 is the most precise. The quantizer divides the DCT coefficient by its corresponding quantum, then rounds to the nearest integer. Large quantums drive small coefficients down to zero. The result: many high frequency coefficients become zero, and therefore easier to code. The low frequency coefficients undergo only minor adjustment. The next section explains how many zeros among the high frequency coefficients leads to efficient compression.

JPEG's Compression Technique After quantization, it is not unusual for more than half of the DCT coefficients to equal zero. JPEG incorporates run-length coding to take advantage of this. For each non-zero DCT coefficient, JPEG records the number of zeros that preceded the number, the number of bits needed to represent the number's amplitude, and the amplitude itself. To consolidate the runs of zeros, JPEG processes DCT coefficients in the zigzag pattern shown in the following figure:

Encoding The number of previous zeros and the bits needed for the current number's amplitude form a pair. Each pair has its own code word, assigned through a variable length code ( for example Huffman, Shannon-Fano or Arithmetic coding). JPEG outputs the code word of the pair, and then the codeword for the coefficient's amplitude (also from a variable length code). After each block, JPEG writes a unique end-of-block sequence to the output stream, and moves to the next block. When finished with all blocks, JPEG writes the end-of-file marker.

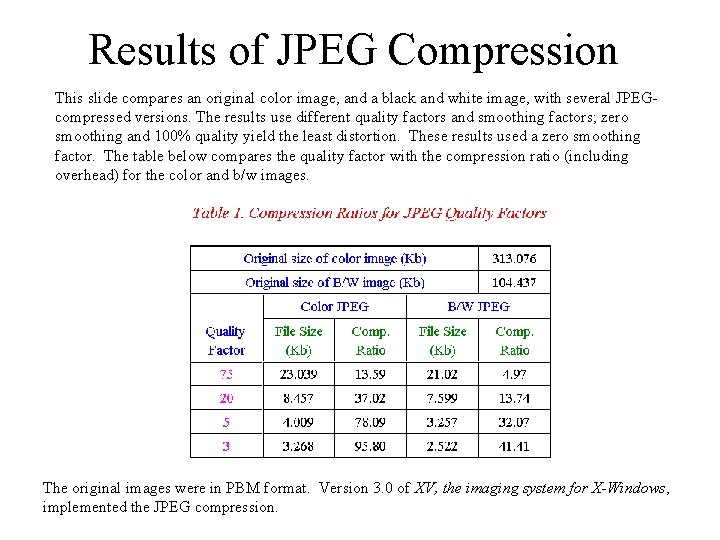
Results of JPEG Compression This slide compares an original color image, and a black and white image, with several JPEGcompressed versions. The results use different quality factors and smoothing factors; zero smoothing and 100% quality yield the least distortion. These results used a zero smoothing factor. The table below compares the quality factor with the compression ratio (including overhead) for the color and b/w images. The original images were in PBM format. Version 3. 0 of XV, the imaging system for X-Windows, implemented the JPEG compression.

Color Images Quality 75 20 5 3 Image Difference Image

Grayscale Images Quality 75 20 5 3 Image Difference Image

Software Many current software libraries include JPEG capability. These include the XV image viewer for the X-Windows system, and the SOLARIS XIL imaging library. Many commercial packages import and export files in JPEG format ( MATLAB, Adobe Photoshop, etc. ). Solaris XIL 1. 1 Imaging Library Programmer's Guide, 1993, Sun Microsystems, Inc. , Revision A, November, pp. 265 - 270. Bradley, John, XV: Image viewer for the X-Windows system, Version 3. 0, programmers guide. 1993. Information on XV is available at http: //www. trilon. com/xv/. C. Thompson and L. Shure, The MATLAB Imaging Processing Toolbox Manual, 1993, Mathworks, Inc. , pp. 1 -94 to 1 -96, 2 -43.

References G. K. Wallace, “The JPEG Still Picture Compression Standard, ” Communications of the ACM, April, 1991, pp. 35. Mark Nelson, The Data Compression Book, 1992, M and T Publishing, Inc. , New York, NY, pp. 347 - 373. An anonymous FTP site for more JPEG documentation is: ftp: //ftp. uu. net/graphics/jpeg. The official JPEG site is: http: //www. jpeg. org