Jose Pablo Reyes 10 5 Describe what a

Jose Pablo Reyes 10 – 5

Describe what a perpendicular bisector is. Explain the perpendicular bisector theorem and its converse. Give 3 examples of each. � Perpendicular bisector – is a line that goes through a segment cutting it into equal parts, creating 90°angles � Perpendicular bisector theorem – if a segment is bisected by a perpendicular line then any point on the perpendicular bisector is equidistant to the end point of the segment � Converse – is a point is equidistant from the endpoint of a segment, then the point lies on the perpendicular bisector of the segment

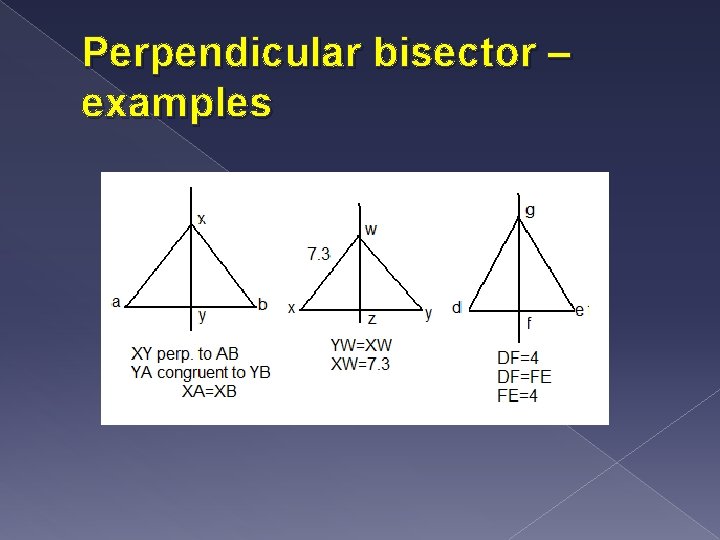
Perpendicular bisector – examples

Describe what an angle bisector is. Explain the angle bisector theorem and its converse. Give at least 3 examples of each. � Angle bisector – line/ray that goes exactly through the half of an angle � Angle bisector theorem – if an angle is bisected by a line/ray then any point on that line is equidistant from both sides of the angle � Converse – if a given point in the interior of an angle is equidistant from the sides of the angle then it is on the bisector of the angle

Angle bisector – examples

Describe what concurrent means. Explain the concurrency of Perpendicular bisectors of a triangle theorem. Explain what a circumcenter is. Give at least 3 examples of each. � Concurrent – three or more lines that intersect at one point � Circumcenter – is the point of congruency in a triangle which is where the points intersect. � Concurrency of perpendicular bisectors of a triangle theorem – perpendicular bisectors of a triangle intersect in a point that is equidistant from the vertices

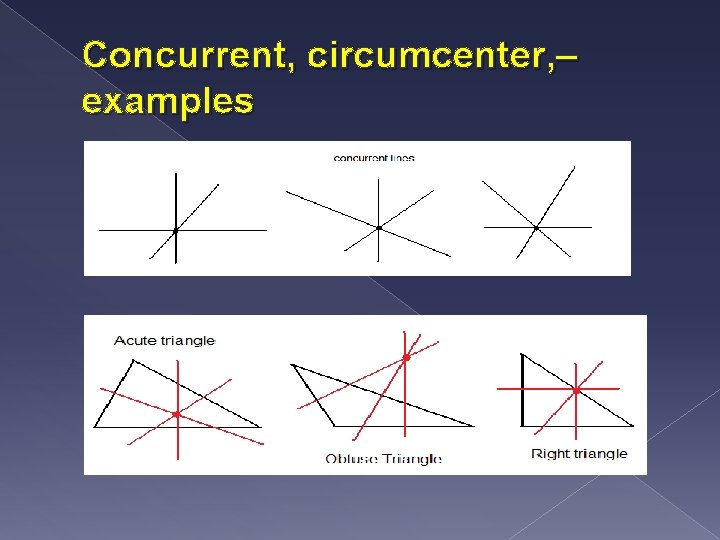
Concurrent, circumcenter, – examples

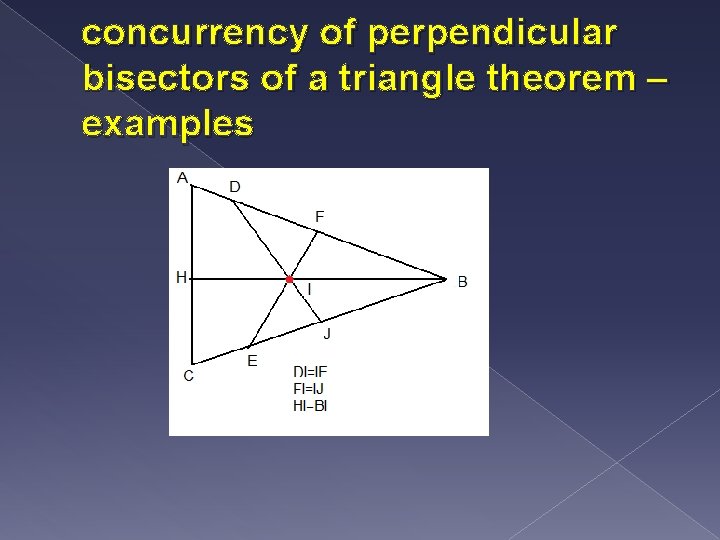
concurrency of perpendicular bisectors of a triangle theorem – examples

Describe the concurrency of angle bisectors of a triangle theorem. Explain what an incenter is. Give at least 3 examples of each. � The concurrency of angle bisectors of a triangle says that the 3 bisectors are congruent � The incenter is the point of concurrency of the angle bisectors, always inside the triangle

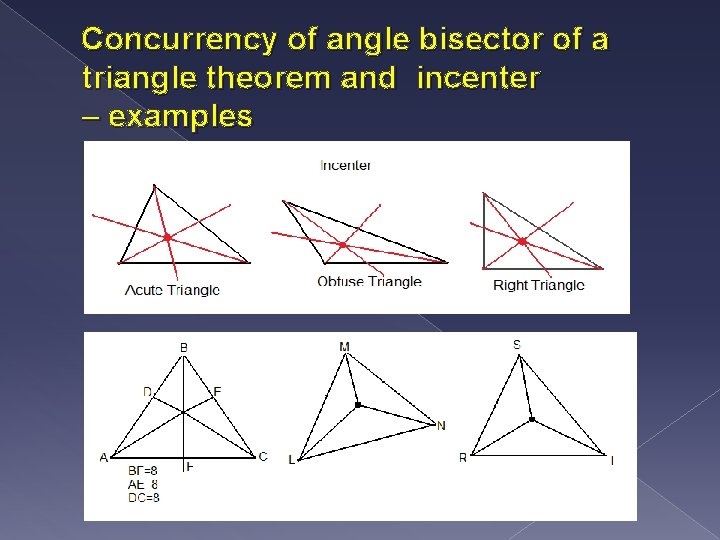
Concurrency of angle bisector of a triangle theorem and incenter – examples

Describe what a median is. Explain what a centroid is. Explain the concurrency of medians of a triangle theorem. Give at least 3 examples of each. � Median – is a segments in which the endpoints are a vertex of the triangle and the midpoint of the opposite side � Centroid – is the point of concurrency of the medians of a triangle. � The centroid of a triangle is 2/3 of the distance from each vertex to the midpoint of the opposite side

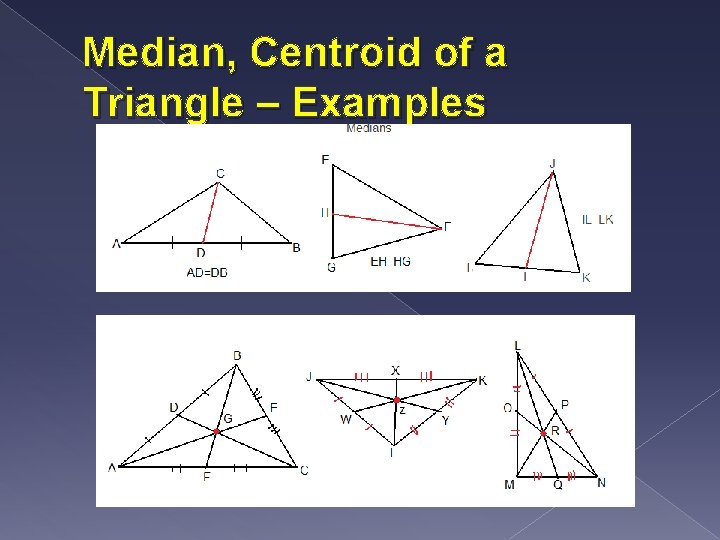
Median, Centroid of a Triangle – Examples

Describe what an altitude of a triangle is. Explain what an orthocenter is. Explain the concurrency of altitudes of a triangle theorem. Give at least 3 examples. � Altitude of a triangle – is a segment from one vertex to the opposite side so the segment is perpendicular to the side. There are 3 altitudes for any triangle, it can be inside, outside or in the triangle � Orthocenter – is the point where three altitudes of a triangle intersect. In obtuse triangles the orthocenter is outside � Concurrency of altitudes of a triangle theorem – the three lines containing the altitudes of a triangle are congruent

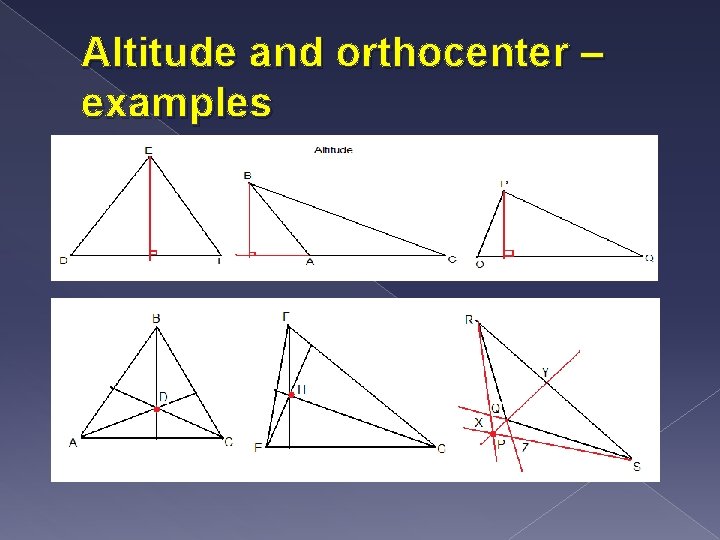
Altitude and orthocenter – examples

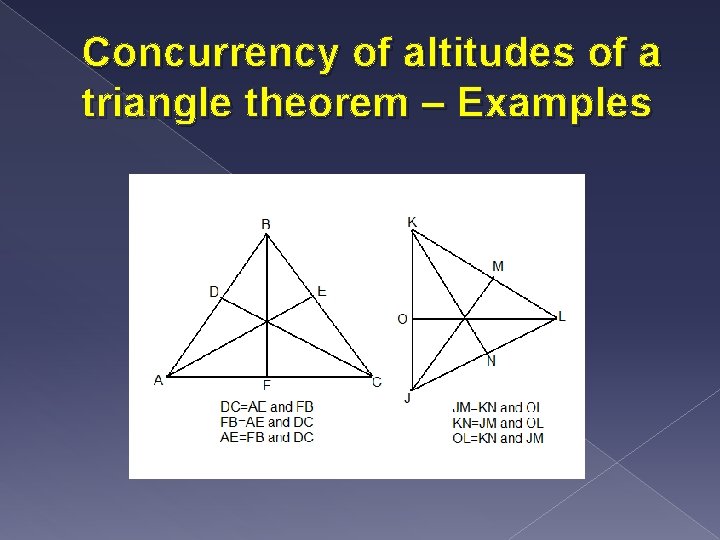
Concurrency of altitudes of a triangle theorem – Examples

Describe what a midsegment is. Explain the midsegment theorem. Give at least 3 examples. � Midsegment of a triangle – any segment that joins the midpoint of two sides of the triangle � Midsegment theorem – a midsegment of a triangle is parallel to the side of the triangle and the length is half the length of that side

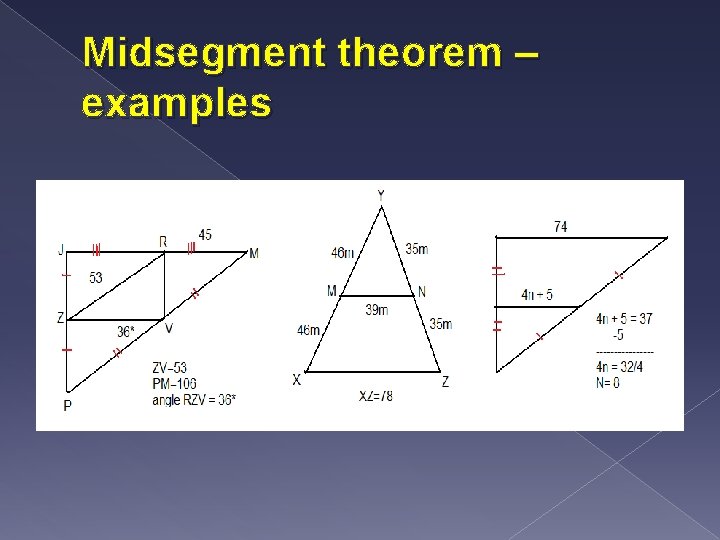
Midsegment theorem – examples

Describe the relationship between the longer and shorter sides of a triangle and their opposite angles. Give at least 3 examples. � Angle side relation in a triangle, the side opposite to the biggest angle will always have the longest length, the side opposite to the smallest angle will have the smallest length

Angle side relation – examples

Describe the exterior angle inequality. Describe the triangle inequality. Give at least 3 examples. � Exterior angle inequality – the exterior angle is greater than the non-adjacent interior angles of the triangle � Triangle inequality – any two sides of a triangle must add up to more than the 3 rd side

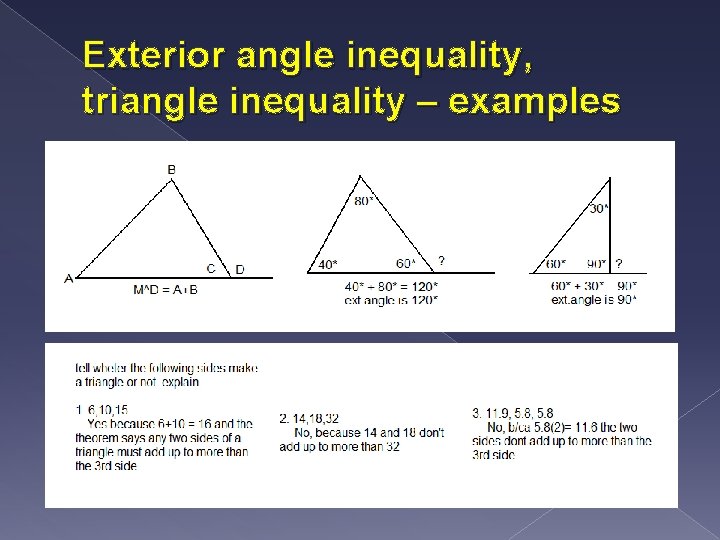
Exterior angle inequality, triangle inequality – examples

Describe how to write an indirect proof. Give at least 3 . examples � Steps to write an indirect proof – 1. Assume that what you are trying to prove is false 2. Try to prove it using the same steps as in normal proofs 3. When you face a contradiction, you have to prove theory true

Indirect proofs – examples

Describe the hinge theorem and its converse. Give at least 3 examples. � Hinge theorem – if two sides of two different triangles are congruent and the angle between them is not congruent, then the triangle with the larger angle will have the longer 3 rd side

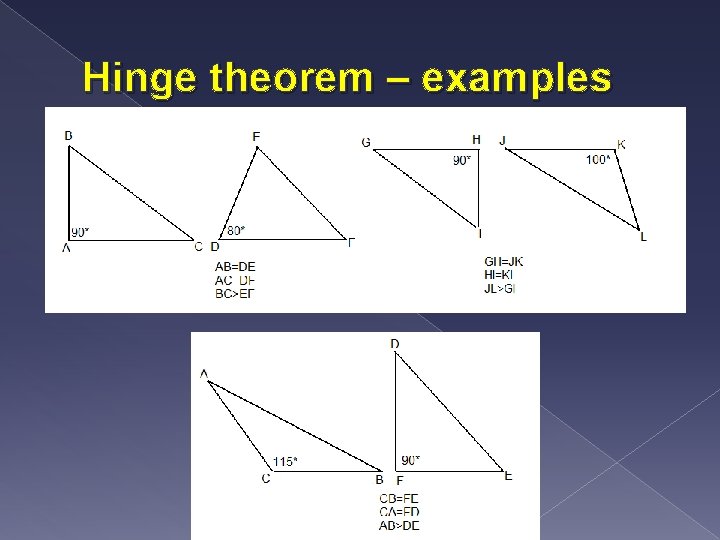
Hinge theorem – examples