Joint Physical Layer Coding and Network Coding for

















- Slides: 49

Joint Physical Layer Coding and Network Coding for Bi-Directional Relaying Makesh Wilson, Krishna Narayanan, Henry Pfister and Alex Sprintson Department of Electrical and Computer Engineering Texas A&M University, College Station, TX

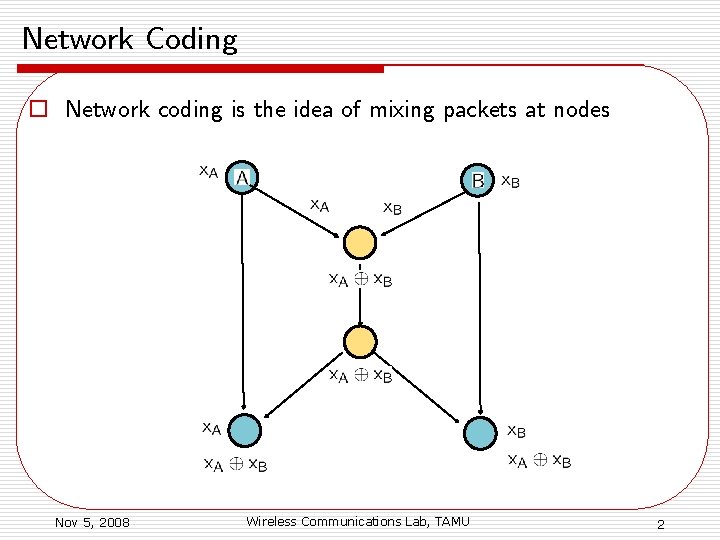
Network Coding o Network coding is the idea of mixing packets at nodes Nov 5, 2008 Wireless Communications Lab, TAMU 2

Characteristics of Wireless Systems o Superposition of signals – signals add at the PHY layer o Broadcast nature – node can broadcast to nodes naturally Nov 5, 2008 Wireless Communications Lab, TAMU 3

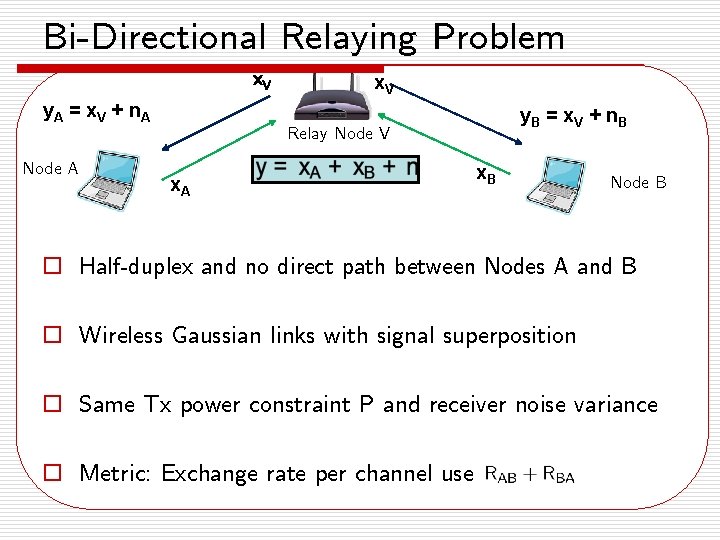
Bi-Directional Relaying Problem x. V y. A = x V + n A y. B = x V + n B Relay Node V Node A x. B Node B o Half-duplex and no direct path between Nodes A and B o Wireless Gaussian links with signal superposition o Same Tx power constraint P and receiver noise variance o Metric: Exchange rate per channel use

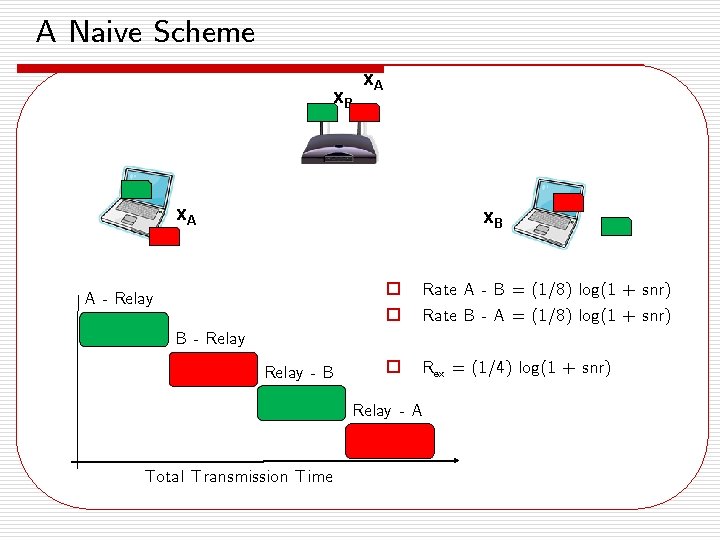
A Naive Scheme x. B x. A x. B A - Relay o o Rate A - B = (1/8) log(1 + snr) Rate B - A = (1/8) log(1 + snr) o Rex = (1/4) log(1 + snr) B - Relay - B Relay - A Total Transmission Time

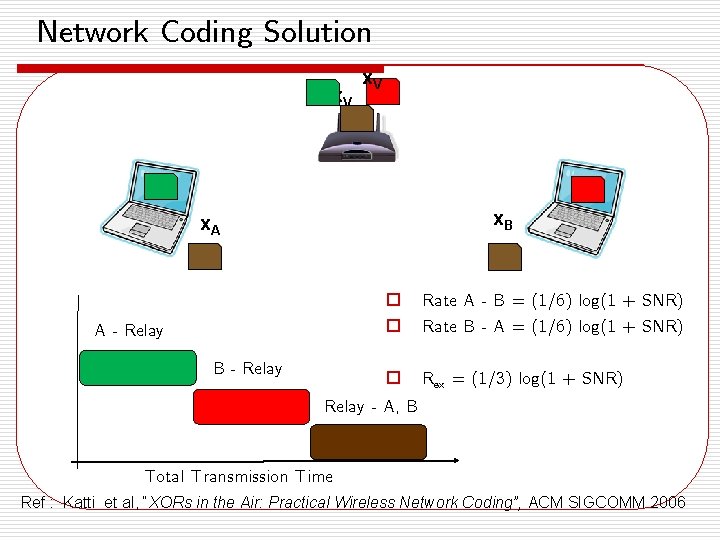
Network Coding Solution x. V x. B x. A A - Relay B - Relay o o Rate A - B = (1/6) log(1 + SNR) Rate B - A = (1/6) log(1 + SNR) o Rex = (1/3) log(1 + SNR) Relay - A, B Total Transmission Time Ref : Katti et al, “XORs in the Air: Practical Wireless Network Coding”, ACM SIGCOMM 2006

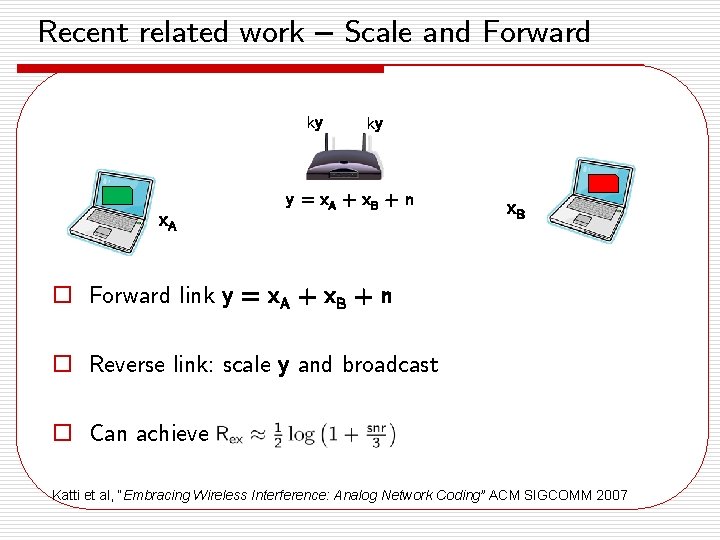
Recent related work – Scale and Forward ky x. A ky y = x A + x. B + n x. B o Forward link y = x. A + x. B + n o Reverse link: scale y and broadcast o Can achieve Katti et al, “Embracing Wireless Interference: Analog Network Coding” ACM SIGCOMM 2007

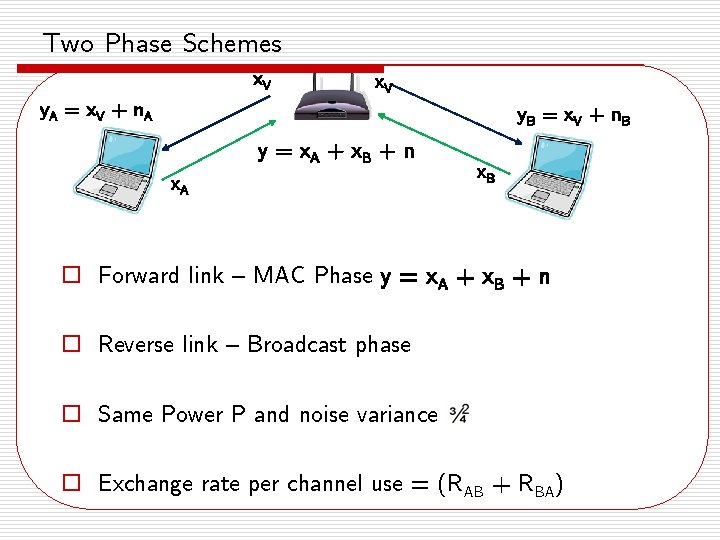
Two Phase Schemes x. V y. A = x V + n. A y. B = x V + n. B y = x A + x. B + n x. A x. B o Forward link – MAC Phase y = x. A + x. B + n o Reverse link – Broadcast phase o Same Power P and noise variance o Exchange rate per channel use = (RAB + RBA)

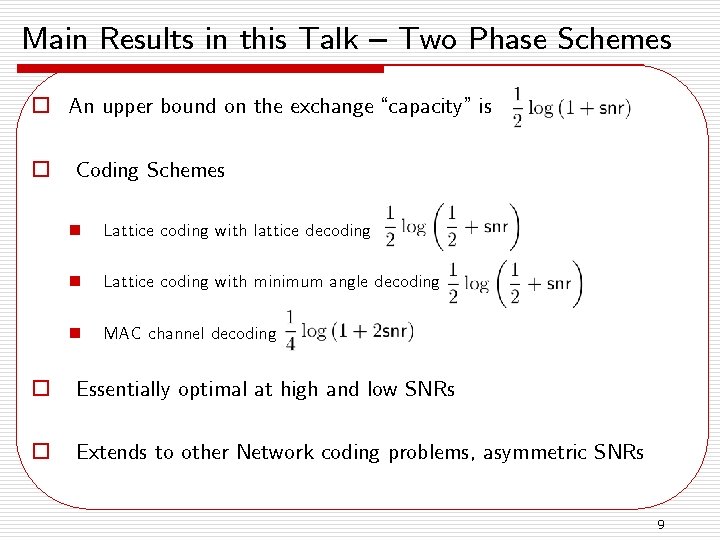
Main Results in this Talk – Two Phase Schemes o An upper bound on the exchange “capacity” is o Coding Schemes n Lattice coding with lattice decoding n Lattice coding with minimum angle decoding n MAC channel decoding o Essentially optimal at high and low SNRs o Extends to other Network coding problems, asymmetric SNRs 9

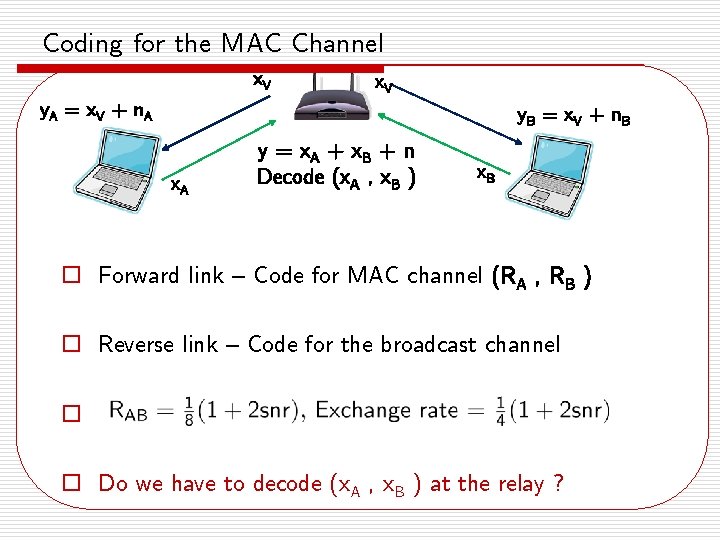
Coding for the MAC Channel x. V y. A = x V + n. A y. B = x V + n. B x. A y = x A + x. B + n Decode (x. A , x. B ) x. B o Forward link – Code for MAC channel (RA , RB ) o Reverse link – Code for the broadcast channel o o Do we have to decode (x. A , x. B ) at the relay ?

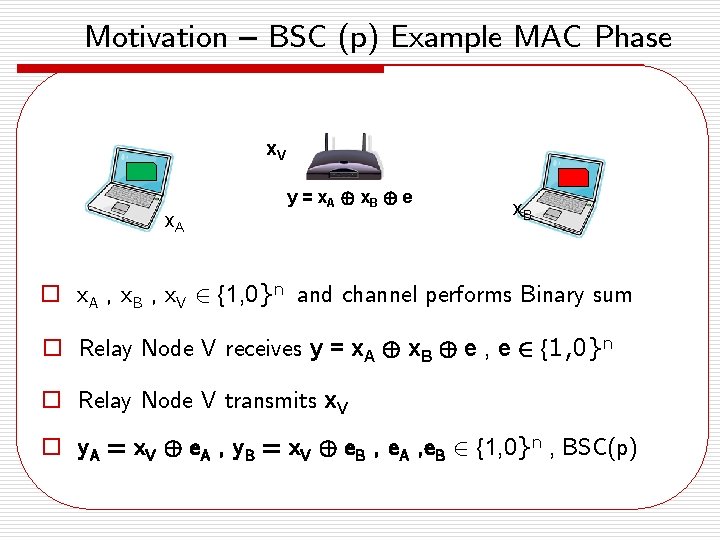
Motivation – BSC (p) Example MAC Phase x. V x. A y = x A © x. B © e x. B o x. A , x. B , x. V 2 {1, 0}n and channel performs Binary sum o Relay Node V receives y = x. A © x. B © e , e 2 {1, 0}n o Relay Node V transmits x. V o y. A = x. V © e. A , y. B = x. V © e. B , e. A , e. B 2 {1, 0}n , BSC(p)

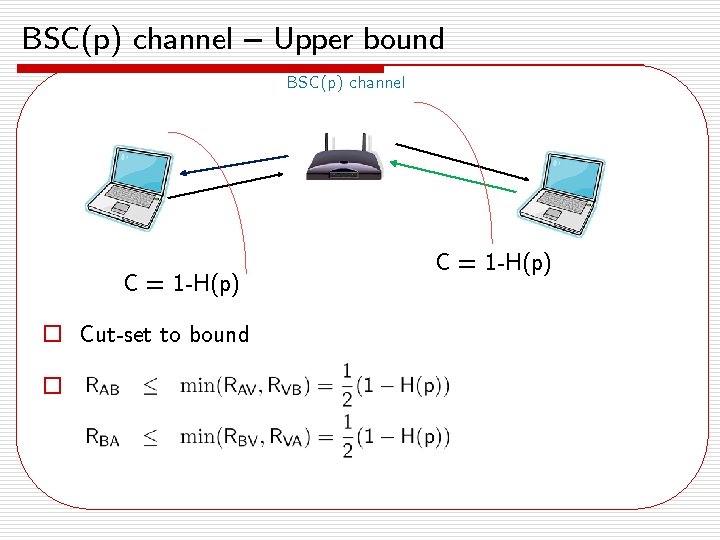
BSC(p) channel – Upper bound BSC(p) channel C = 1 -H(p) o Cut-set to bound o C = 1 -H(p)

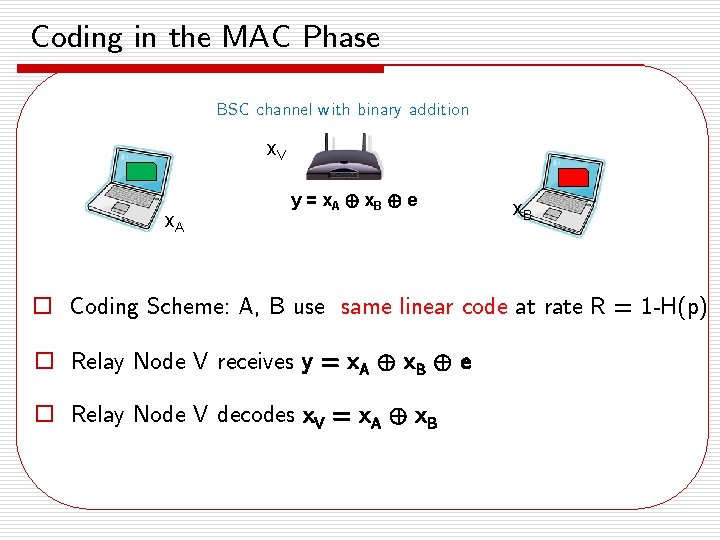
Coding in the MAC Phase BSC channel with binary addition x. V x. A y = x A © x. B © e x. B o Coding Scheme: A, B use same linear code at rate R = 1 -H(p) o Relay Node V receives y = x. A © x. B © e o Relay Node V decodes x. V = x. A © x. B

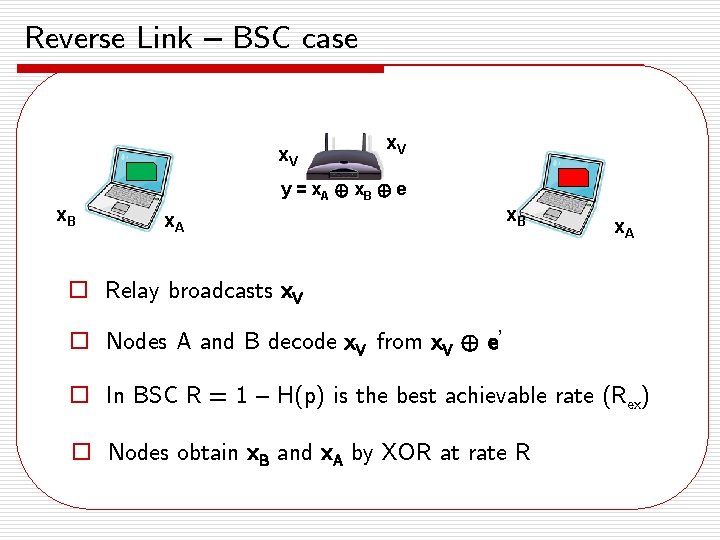
Reverse Link – BSC case x. V y = x A © x. B © e x. B x. A o Relay broadcasts x. V o Nodes A and B decode x. V from x. V © e’ o In BSC R = 1 – H(p) is the best achievable rate (Rex) o Nodes obtain x. B and x. A by XOR at rate R

Main point Linearity was important in the uplink Structured codes outperform random codes

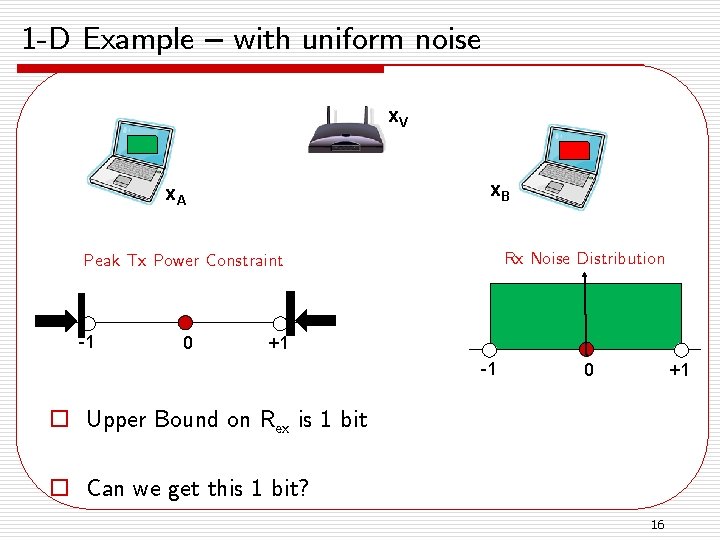
1 -D Example – with uniform noise x. V x. B x. A Rx Noise Distribution Peak Tx Power Constraint -1 0 +1 -1 +1 0 o Upper Bound on Rex is 1 bit o Can we get this 1 bit? 16

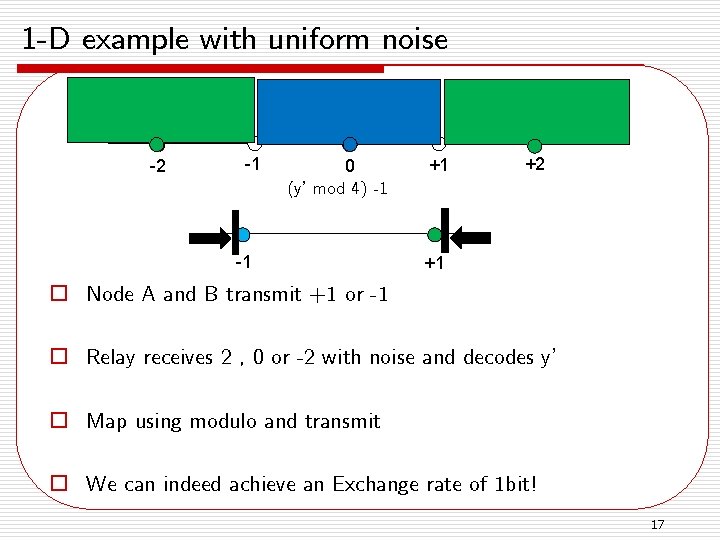
1 -D example with uniform noise -2 -1 0 (y’ mod 4) -1 -1 +1 +2 +1 o Node A and B transmit +1 or -1 o Relay receives 2 , 0 or -2 with noise and decodes y’ o Map using modulo and transmit o We can indeed achieve an Exchange rate of 1 bit! 17

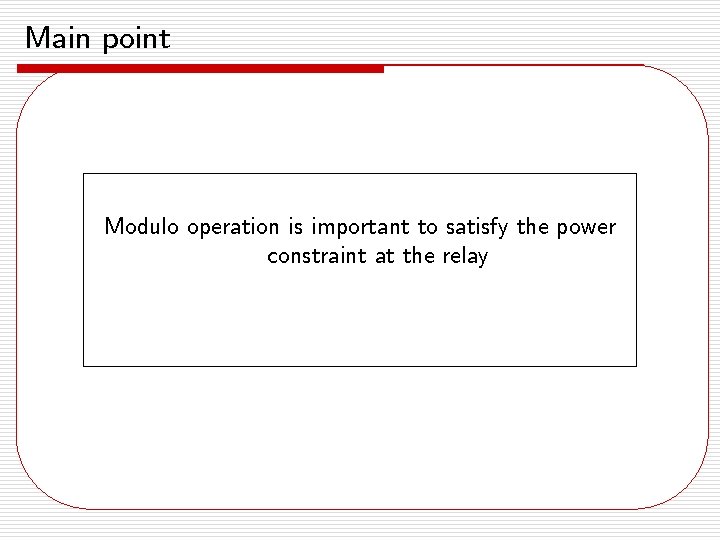
Main point Modulo operation is important to satisfy the power constraint at the relay

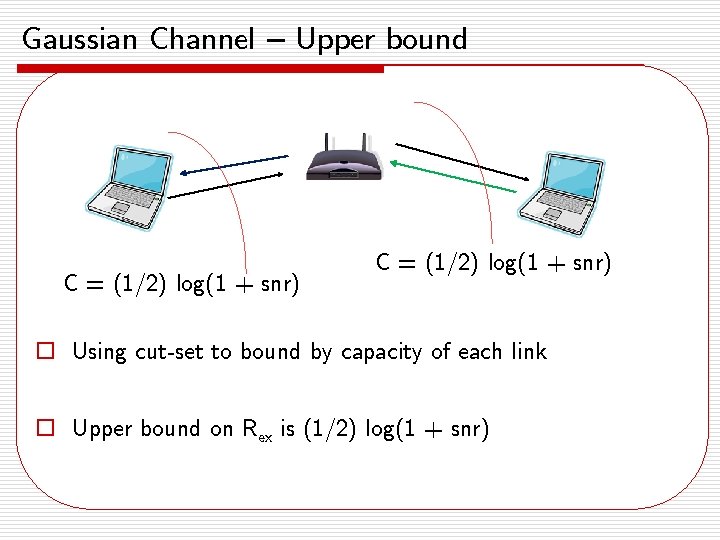
Gaussian Channel – Upper bound C = (1/2) log(1 + snr) o Using cut-set to bound by capacity of each link o Upper bound on Rex is (1/2) log(1 + snr)

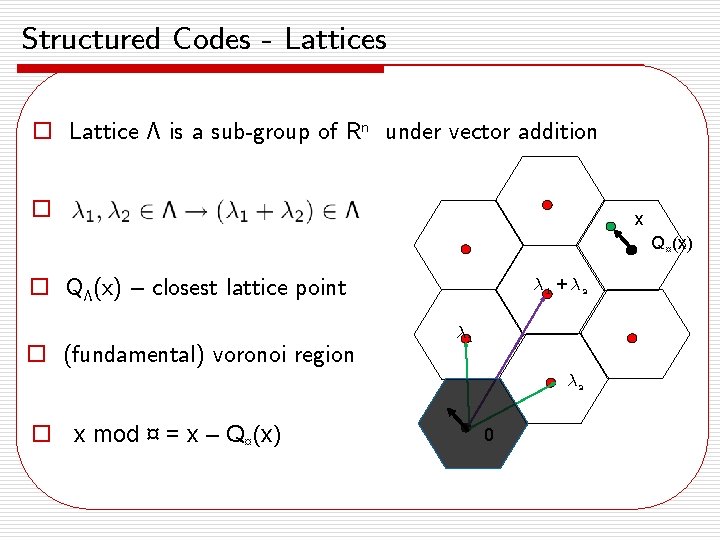
Structured Codes - Lattices o Lattice ¤ is a sub-group of Rn under vector addition o x Q¤(x) o Q¤(x) – closest lattice point o (fundamental) voronoi region ¸ 1 + ¸ 2 ¸ 1 ¸ 2 o x mod ¤ = x – Q¤(x) 0

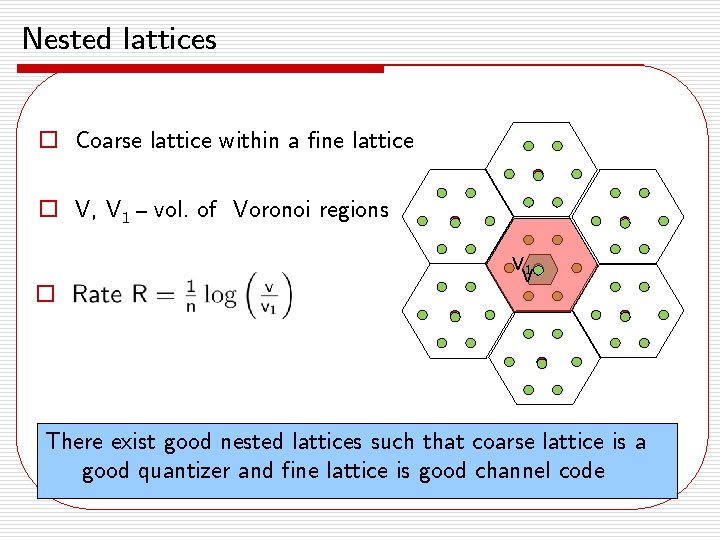
Nested lattices o Coarse lattice within a fine lattice o V, V 1 – vol. of Voronoi regions o V 1 V There exist good nested lattices such that coarse lattice is a good quantizer and fine lattice is good channel code

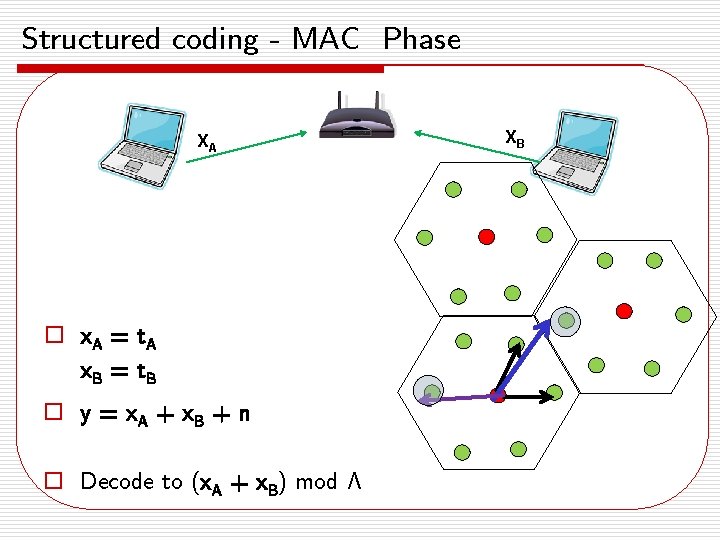
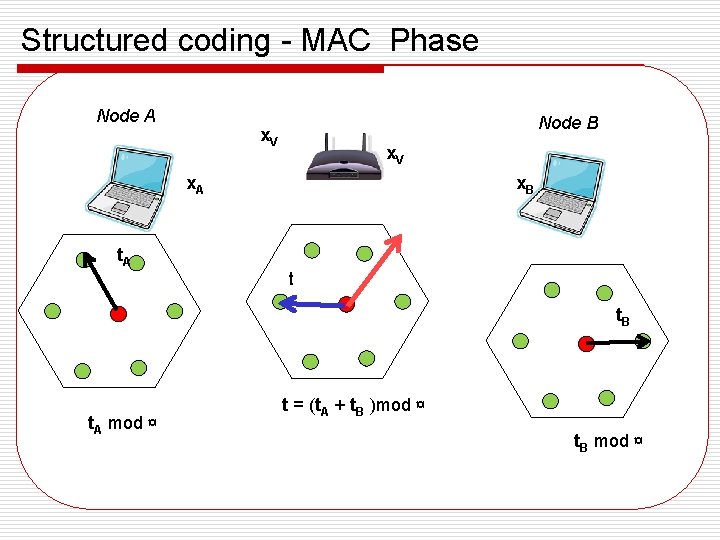
Structured coding - MAC Phase XA o x. A = t A x. B = t B o y = x. A + x. B + n o Decode to (x. A + x. B) mod ¤ XB

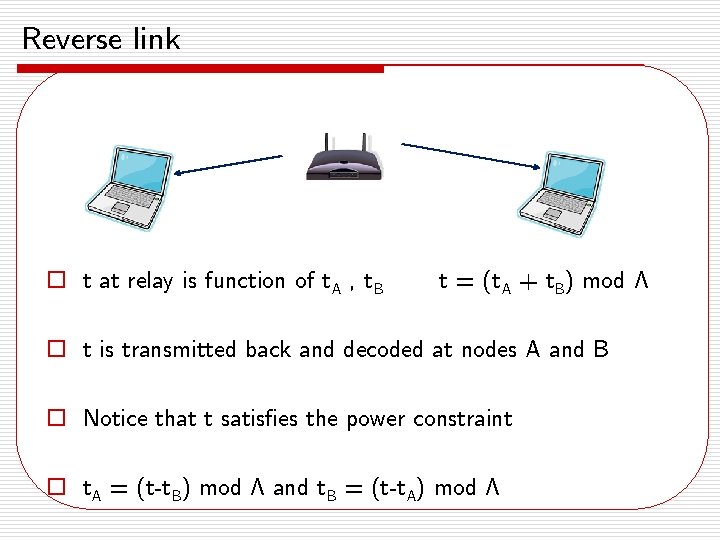
Reverse link o t at relay is function of t. A , t. B t = (t. A + t. B) mod ¤ o t is transmitted back and decoded at nodes A and B o Notice that t satisfies the power constraint o t. A = (t-t. B) mod ¤ and t. B = (t-t. A) mod ¤

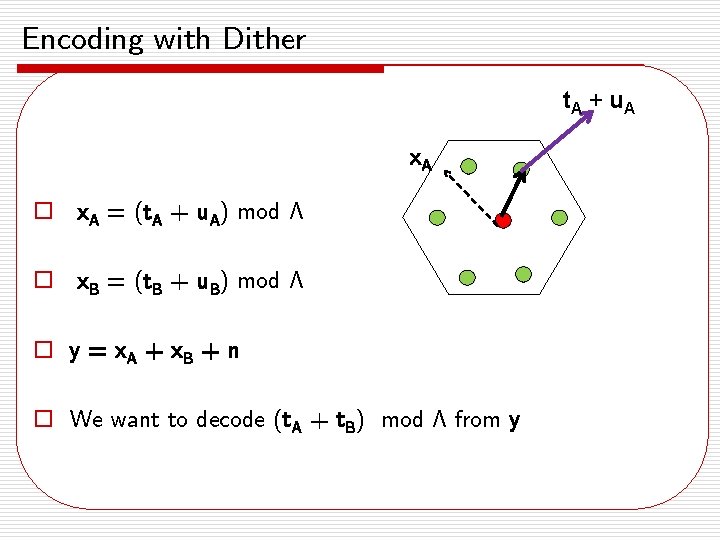
Encoding with Dither t. A + u A x. A o x. A = (t. A + u. A) mod ¤ o x. B = (t. B + u. B) mod ¤ o y = x A + x. B + n o We want to decode (t. A + t. B) mod ¤ from y

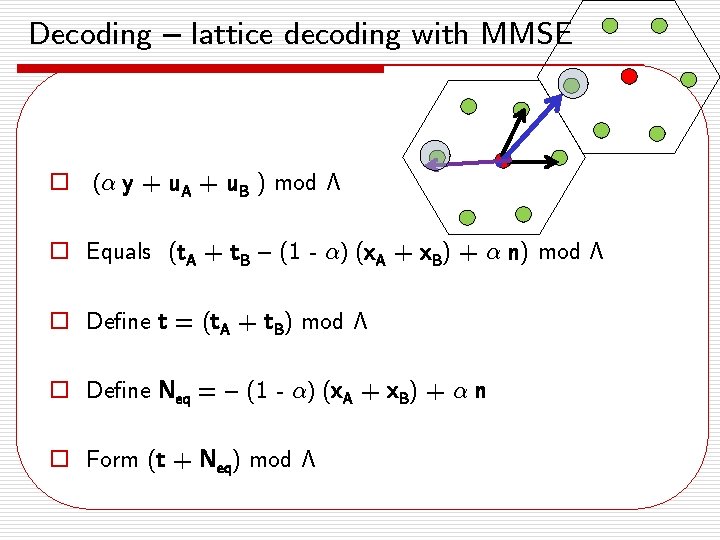
Decoding – lattice decoding with MMSE o (® y + u. A + u. B ) mod ¤ o Equals (t. A + t. B – (1 - ®) (x. A + x. B) + ® n) mod ¤ o Define t = (t. A + t. B) mod ¤ o Define Neq = – (1 - ®) (x. A + x. B) + ® n o Form (t + Neq) mod ¤

Achievable rate o Theorem: Using Nested lattices a rate of (1/2) log (0. 5 + snr) is achievable o The second moment of Neq is (2 P ¾ 2)/(2 P + ¾ 2) o The second moment of t is P o Hence rate is (1/2) log (0. 5 + snr) – so many fine lattice points in Coarse lattice o At high SNR approx equal to (1/2) log (1 + snr) , the upper bound

More Proof details o Follows Erez and Zamir results for Modulo Lattice Additive Noise (MLAN) Channel o (t mod ¤ + Neq) mod ¤ o Neq can be approximated by Gaussian o t mod ¤ is uniformly distributed o Poltyrev exponents can be calculated

Low/medium SNR regime o Does Gaussian MAC to achieve CAB + CBA = (1/4) log(1 + 2 snr) o Note relay can decode both x. A and x. B o Does Slepian Wolf Coding in reverse link

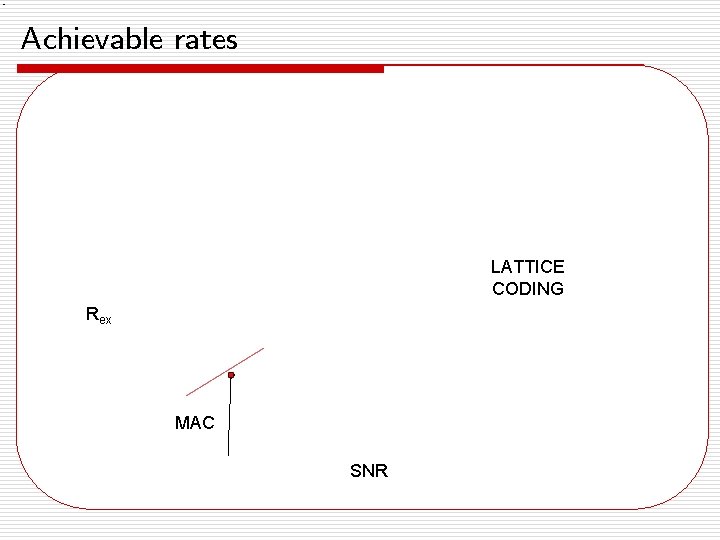
Achievable rates LATTICE CODING Rex MAC SNR

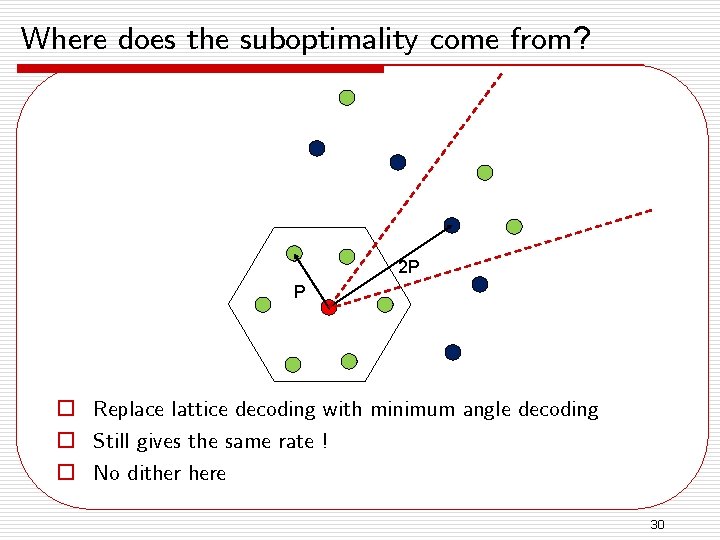
Where does the suboptimality come from? 2 P P o Replace lattice decoding with minimum angle decoding o Still gives the same rate ! o No dither here 30

Where does the sub-optimality come from? 2 P P o Not all lattice points at radius of 2 P are code words at low rates! o Prior distribution of (x. A + x. B) is not uniform ! 31

Does it Generalize? o Exchanging information between nodes in Multi-hop o Holds for general networks like the Butterfly network o Asymmetric channel gains

Multiple hops o Multi-hop with each node can communicate with only two immediate neighbors o Each node can not broadcast and listen in the same transmission slot o Again (1/2) log (0. 5 + snr) can be achieved

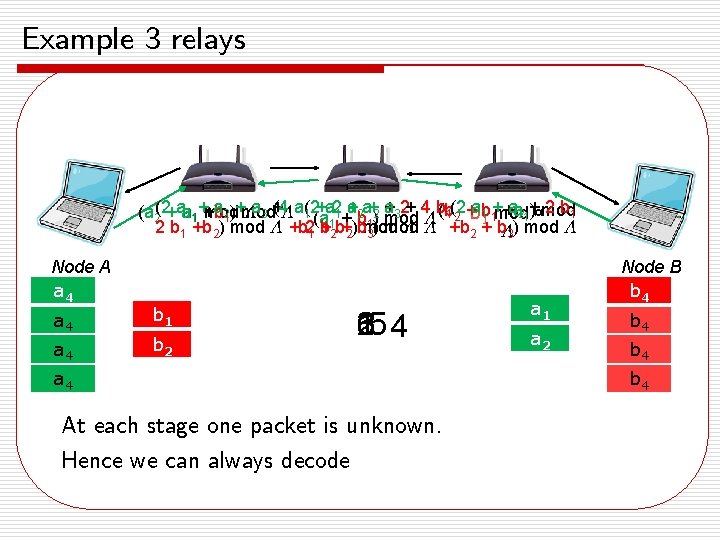
Example 3 relays a 2)+mod a + (4 a(2+a 2 a +2 a+2 a +32+ 4 b(b 1(2 a 1 b 1+mod a 21+ 2 b 1 +a )¤mod (a 2(2+aa 11++b mod b 2 + 1 ¤ 3 ¤ 1 (a 1+ b 1 ) mod ¤ 1) mod 2 b 1 +b 2) mod ¤ +b 21 b +12 b+2)bmod ¤ ¤ +b 2 + b¤ 3) mod ¤ 3 Node A a 4132 a 43 b 1 b 2 6 25 4 1 3 a 4 At each stage one packet is unknown. Hence we can always decode a 1 a 2 Node B b 4132 b 43 b 4

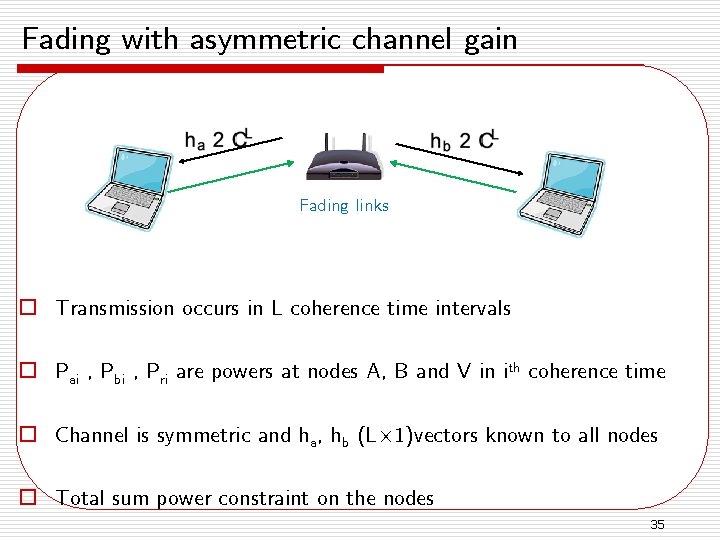
Fading with asymmetric channel gain Fading links o Transmission occurs in L coherence time intervals o Pai , Pbi , Pri are powers at nodes A, B and V in ith coherence time o Channel is symmetric and ha, hb (L£ 1)vectors known to all nodes o Total sum power constraint on the nodes 35

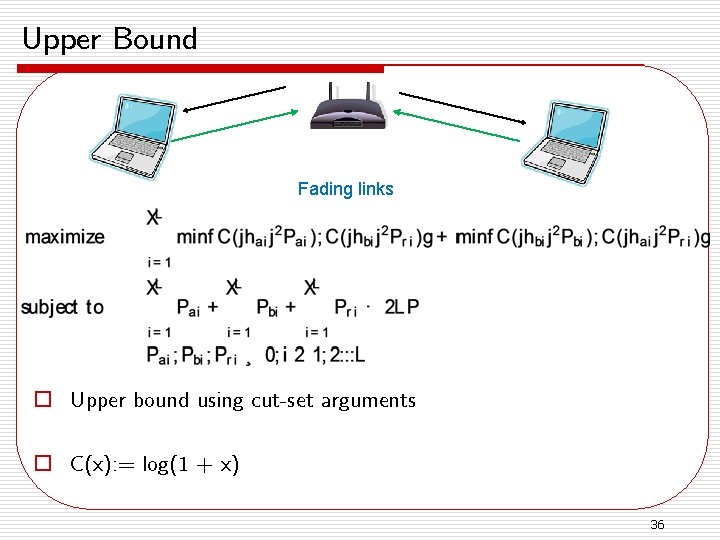
Upper Bound Fading links o Upper bound using cut-set arguments o C(x): = log(1 + x) 36

Analysis for L = 1 o For · 2 small o For · 2 large o Hence o Or 37

Achievable scheme using channel inversion o D(snr): = Rate using Lattice/MAC based scheme for given snr 38

Analysis for L = 1 o Here · 2 Pa = Pb 39

Comparison of the Bounds for arbitrary L o Theorem: For the problem setup, for arbitrary L and ¢ = 0. 5, under the high snr approximation, the channel inversion scheme with Lattices is at max a constant (0. 09 bits per complex channel use), away from the upper bound! 40

Does it Generalize? o Exchanging information between nodes in Multi-hop o Holds for general networks like the Butterfly network

Conclusion o Structured codes are advantageous in wireless networking o Results for high and low snr show are nearly optimal o Extension to multihop channels and asymmetric gains o Many challenges remain n n Capacity is unknown –only 2 -phase schemes were considered Channel has to be known Even if channel is known can we get 0. 5 log(1+snr) ? Practical lattice codes to achieve these rates

Structured coding - MAC Phase Node A Node B x. V x. A x. B t. A t t. B t. A mod ¤ t = (t. A + t. B )mod ¤ t. B mod ¤

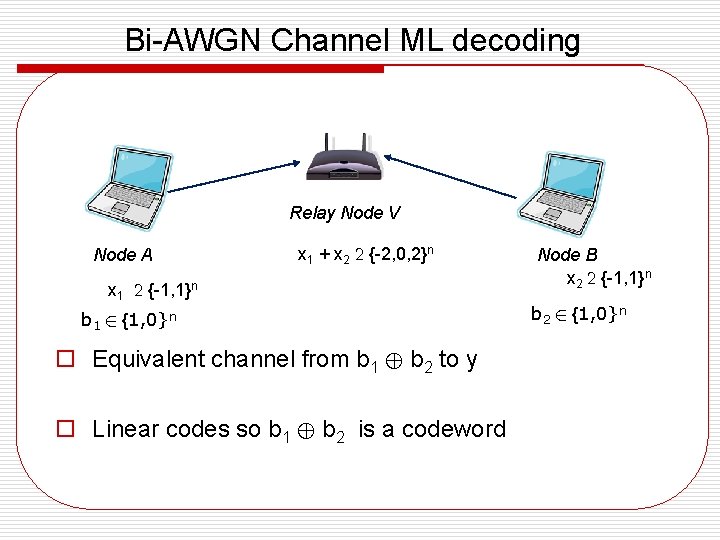
Bi-AWGN Channel ML decoding Relay Node V Node A x 1 + x 2 2 {-2, 0, 2}n x 1 2 {-1, 1}n b 1 2 {1, 0}n o Equivalent channel from b 1 © b 2 to y o Linear codes so b 1 © b 2 is a codeword Node B x 2 2 {-1, 1}n b 2 2 {1, 0}n

Conjecture ML decoding Lattices o Can’t do better than (1/2)log ( 0. 5 + SNR) with ML o Minkowski-Hlawka for existence of lattices o Blichfeldts Principle for Concentration of codewords ideas o Assuming uniform distribution yeilds good concentration

Concentration at 2 P o Sum x. A + x. B will be in 2 P x 1 Use Blichfeldt for lattice equivalent x 2

Projecting to inner sphere Project Codewords to inner sphere Use Minkowski – Hlawka to show existence of Lattice Calculate probability of error

Connection to Lattices o Using Blichfeldts theorem we can establish concentration for lattices also o Minkowski-Hlawka theorem can be used to perform ML Decoding o Again it appears we can get only (1/2) log (0. 5 + SNR)

References o
 Apa itu selective coding
Apa itu selective coding Contoh open coding
Contoh open coding Physical layer coding violations
Physical layer coding violations Character stuffing and destuffing program in c
Character stuffing and destuffing program in c The basic unit of a physical network (osi layer 1) is the:
The basic unit of a physical network (osi layer 1) is the: Pigmented layer and neural layer
Pigmented layer and neural layer Git layers
Git layers Secure socket layer and transport layer security
Secure socket layer and transport layer security Secure socket layer and transport layer security
Secure socket layer and transport layer security Secure socket layer and transport layer security
Secure socket layer and transport layer security Secure socket layer and transport layer security
Secure socket layer and transport layer security Coding dna and non coding dna
Coding dna and non coding dna Joint
Joint Depression movement
Depression movement Layer 6 presentation layer
Layer 6 presentation layer Layer 2 e layer 3
Layer 2 e layer 3 Layer-by-layer assembly
Layer-by-layer assembly Layer 2 vs layer 3 bitstream
Layer 2 vs layer 3 bitstream Block coding in data link layer
Block coding in data link layer Axial coding vs open coding
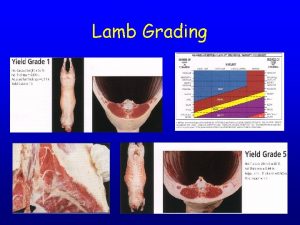
Axial coding vs open coding A grade lamb
A grade lamb Uncovertebral joint
Uncovertebral joint Venture meaning in accounting
Venture meaning in accounting Lamb carcass grading
Lamb carcass grading Classic ethernet mac sublayer protocol
Classic ethernet mac sublayer protocol What is the purpose of the osi physical layer?
What is the purpose of the osi physical layer? Physical layer in osi model examples
Physical layer in osi model examples Physical layer function
Physical layer function Physical architecture layer design
Physical architecture layer design Physical architecture layer design
Physical architecture layer design Physical layer transmission media
Physical layer transmission media Physical architecture layer design
Physical architecture layer design Data link osi layer
Data link osi layer Characteristics of llc sublayer
Characteristics of llc sublayer Physical layer encoding
Physical layer encoding The physical layer concerns with
The physical layer concerns with Physical layer encoding
Physical layer encoding Hub layer 1
Hub layer 1 What is the basic purpose of the osi physical layer
What is the basic purpose of the osi physical layer Physical layer pipe
Physical layer pipe Spacewire physical layer
Spacewire physical layer Analog digital transmission
Analog digital transmission Physical layer in lte
Physical layer in lte 802 3
802 3 Transmission media in computer network
Transmission media in computer network Network layer design
Network layer design Comparison of virtual circuit and datagram subnets
Comparison of virtual circuit and datagram subnets Fungsi utama network layer
Fungsi utama network layer Network layer design issues
Network layer design issues Introduction to network layer
Introduction to network layer