John Napier 1550 1617 matematico scozzese invent i
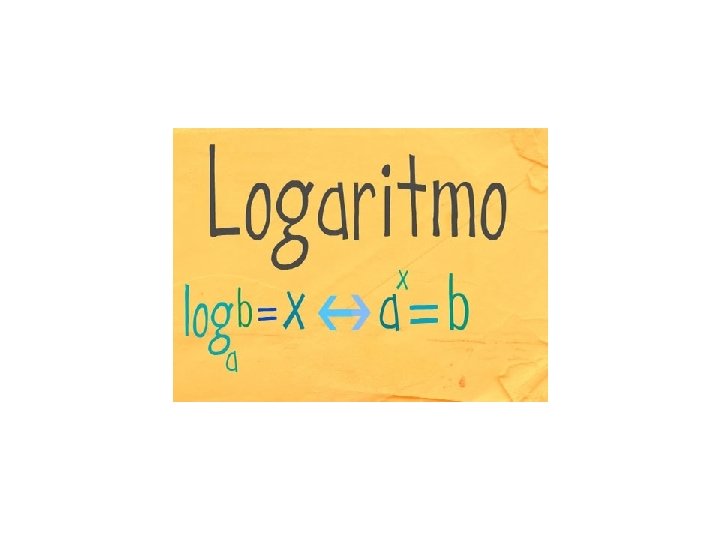





















- Slides: 28

John Napier (1550 -1617), matematico scozzese inventò i LOGARITMI ed essi costituirono lo strumento di calcolo fondamentale fino all'avvento delle moderne macchine da calcolo. Essi permettono di eseguire moltiplicazioni e divisioni semplicemente come somme o differenze. Fu Nepero a coniare il termine logaritmo (dal greco: lògon [ragione, intesa qui nel senso usato nelle progressioni geometriche, cioè rapporto] e arithmòs [numero]: numero razionale, nel senso di numero "artificiale", creato dalla ragione). La sua discussione sui logaritmi appare nella celebre opera " Mirifici logarithmorum canonis descriptio" del 1614. Con essa egli sperava di fornire uno strumento che rendesse molto più veloci i calcoli degli astronomi.

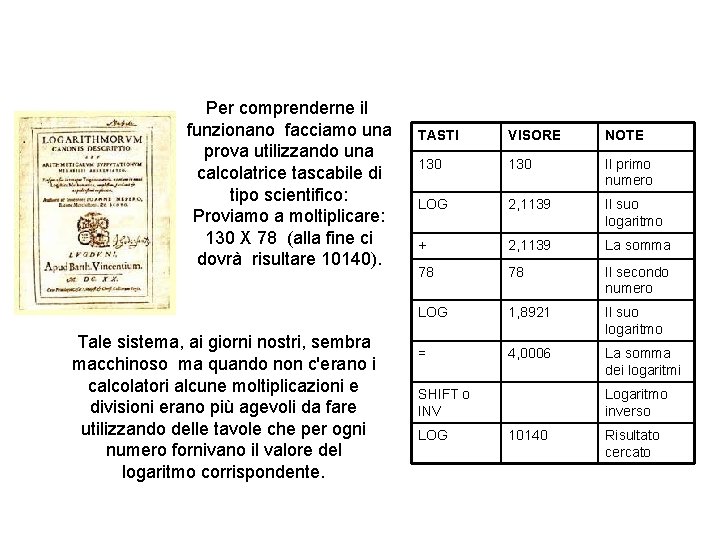
Per comprenderne il funzionano facciamo una prova utilizzando una calcolatrice tascabile di tipo scientifico: Proviamo a moltiplicare: 130 X 78 (alla fine ci dovrà risultare 10140). Tale sistema, ai giorni nostri, sembra macchinoso ma quando non c'erano i calcolatori alcune moltiplicazioni e divisioni erano più agevoli da fare utilizzando delle tavole che per ogni numero fornivano il valore del logaritmo corrispondente. TASTI VISORE NOTE 130 Il primo numero LOG 2, 1139 Il suo logaritmo + 2, 1139 La somma 78 78 Il secondo numero LOG 1, 8921 Il suo logaritmo = 4, 0006 La somma dei logaritmi SHIFT o INV LOG Logaritmo inverso 10140 Risultato cercato

Oggi i logaritmi trovano svariate applicazioni in diversi campi: • in fisica (termologia): ad esempio, se si porta ad ebollizione l’acqua e poi si misura, ad intervalli regolari (per es. ogni due minuti) la temperatura T dell’acqua che si raffredda, le misurazioni effettuate seguono un andamento logaritmico decrescente; • in chimica: il calcolo del p. H è il valore del logaritmo negativo in base 10 della concentrazione degli ioni idrogeno (H+) in una soluzione; • in astronomia: la luminosità delle stelle (“magnitudine”) viene calcolata in scala logaritmica, in funzione della temperatura (diagramma H-R: Hertzsprung-Russell); • in sismologia: l’intensità dei terremoti, misurata come “magnitudo” con la scala Richter, calcola l’ampiezza delle onde sismiche con una formula logaritmica; • in finanziaria: alcuni regimi finanziari applicano formule esponenziali e logaritmiche per il calcolo dei tassi d’interesse; • in musica: tra una nota musicale e la successiva, l’aumento di frequenza dell’onda sonora segue un andamento logaritmico crescente.

Si dice logaritmo in base a di un numero b l’esponente c che si deve dare ad a per avere b, in simboli si scrive: Questo significa che le scritture e si equivalgono. a si chiama base del logaritmo e b argomento del logaritmo.

Alcune considerazioni importanti: • il numero a deve essere positivo e diverso da 1; • il numero b, essendo il risultato di una potenza di base positiva, deve essere positivo; • il numero c, invece, rappresentando l’esponente da dare ad a per avere b, può essere sia positivo, che negativo, che nullo.

Esempi Calcolare i seguenti logaritmi: 1. Occorre chiedersi: qual è l'esponente che devo dare a 2 per ottenere 8? 2. Occorre chiedersi: qual è l'esponente che devo dare a 3 per ottenere 27? 3. Occorre chiedersi: qual è l'esponente che devo dare a 7 per ottenere 1/49?

Dalla definizione, supponendo a > 0, con a ≠ 1 e b > 0, discendono le seguenti proprietà fondamentali: • cioè logab è l’esponente che si deve dare ad a per avere b; • loga a = 1 cioè 1 è l’esponente che si deve dare ad a per avere a; • loga 1 = 0 cioè 0 è l’esponente che si deve dare ad a per avere 1.

FUNZIONE LOGARITMICA Ora che abbiamo visto la definizione di logaritmo possiamo esprimere la relazione che ci consente di scrivere l’equazione della funzione inversa di quella esponenziale. Infatti, dalla relazione y = ax ricaviamo che x = loga y. Scambiando poi il nome della variabile otteniamo la funzione inversa. La funzione y = loga x si dice funzione logaritmica. Possiamo osservare che: dominio e codominio si scambiano i grafici delle due funzioni sono simmetrici rispetto alla bisettrice del primo e terzo quadrante la curva logaritmica è crescente se è a >1, decrescente se 0 < a < 1, interseca l'asse delle ascisse nel punto di coordinate (1, 0)

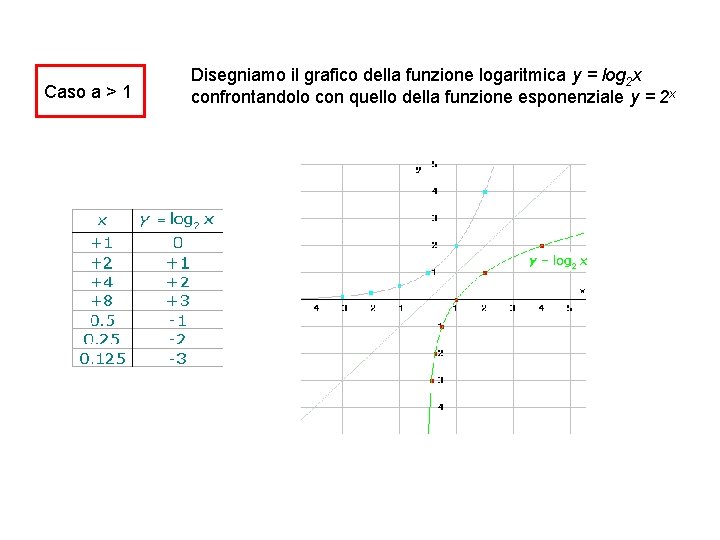
Caso a > 1 Disegniamo il grafico della funzione logaritmica y = log 2 x confrontandolo con quello della funzione esponenziale y = 2 x

Cosa si può osservare? il grafico giace tutto nel semipiano positivo delle ascisse; il grafico non interseca l’asse delle ordinate; il grafico interseca l’asse delle ascisse nel punto (1, 0); la funzione è monotona crescente (cresce sempre più lentamente al crescere della x); ha come asintoto verticale l'asse delle y; il grafico è il simmetrico rispetto alla bisettrice del primo e terzo quadrante di quello della funzione esponenziale corrispondente.

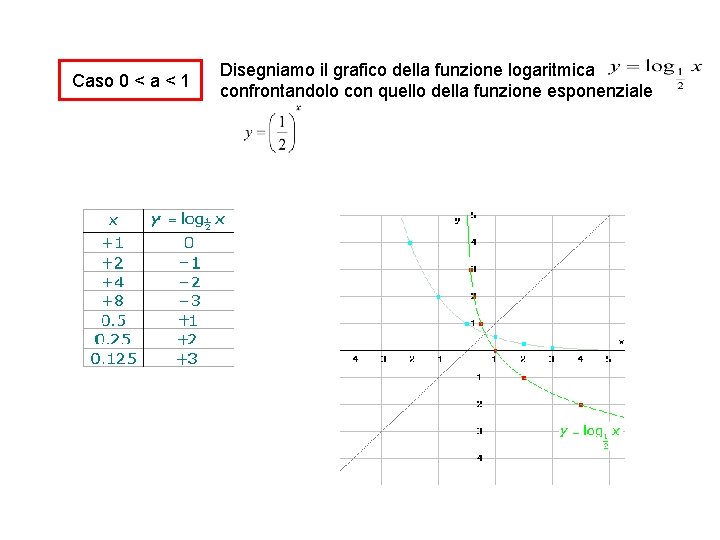
Caso 0 < a < 1 Disegniamo il grafico della funzione logaritmica confrontandolo con quello della funzione esponenziale

Cosa si può osservare? il grafico giace nel semipiano positivo delle ascisse; il grafico non interseca l’asse delle ordinate; il grafico interseca l’asse delle ascisse nel punto (1, 0); ha come asintoto verticale l'asse delle y; la funzione è monotona decrescente; il grafico è il simmetrico rispetto alla bisettrice del primo e terzo quadrante di quello della funzione esponenziale corrispondente.

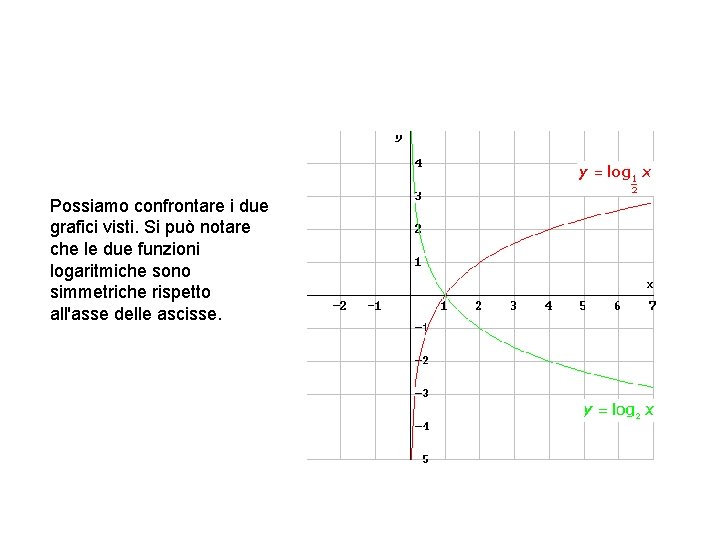
Possiamo confrontare i due grafici visti. Si può notare che le due funzioni logaritmiche sono simmetriche rispetto all'asse delle ascisse.

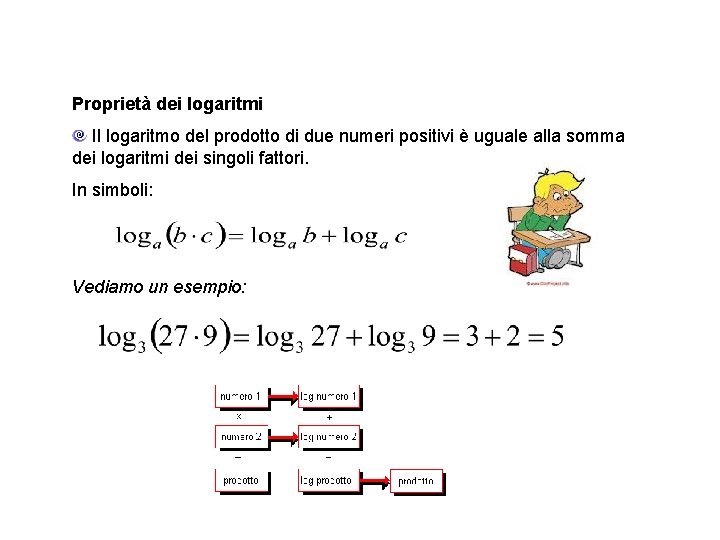
Proprietà dei logaritmi Il logaritmo del prodotto di due numeri positivi è uguale alla somma dei logaritmi dei singoli fattori. In simboli: Vediamo un esempio:

Naturalmente vale anche il contrario: la somma di due logaritmi aventi la stessa base è uguale al logaritmo del prodotto dei due argomenti. Alla scrittura non si può applicare la proprietà perché i logaritmi non hanno la stessa base.

Il logaritmo del quoziente di due numeri positivi è uguale alla differenza fra il logaritmo del dividendo e quello del divisore. In simboli: Vediamo un esempio:

Anche questa proprietà può essere letta in senso inverso: la differenza di due logaritmi aventi la stessa base è uguale al logaritmo del quoziente dei due argomenti.

Il logaritmo della potenza di un numero positivo è uguale al prodotto fra l’esponente della potenza ed il logaritmo del numero. In simboli: Vediamo degli esempi:

Il logaritmo di un radicale è uguale al quoziente fra il logaritmo del radicando e l’indice del radicale. In simboli: Vediamo degli esempi:

L’insieme dei logaritmi in una data base a di ciascun numero positivo si chiama di solito sistema di logaritmi in base a. In un’espressione si possono ritrovare logaritmi in basi diverse, si pone quindi il problema di passare da una base all’altra. La formula che ci consente questo è la seguente: Trasformiamo i seguenti logaritmi nelle base indicate. log 5 24 in base 2 Applichiamo la formula: in base 8:

I risultati che abbiamo ottenuto negli esempi fatti non ci hanno dato però informazioni precise sul valore numerico di un logaritmo. Ad esempio quanto vale log 29? Poiché i sistemi di logaritmi sono infiniti, è impensabile cercare di trovare il valore numerico del logaritmo di ogni numero reale positivo in una base qualunque. I sistemi di logaritmi che si usano comunemente sono quelli in base 10 ed in base e, detti rispettivamente logaritmi decimali e logaritmi naturali o neperiani dal nome del matematico inglese John Napier a cui si attribuisce l’invenzione dei logaritmi. Essi si indicano con simboli particolari evitando così di ripetere ogni volta la base: log 10 x si indica con log x loge x si indica con ln x Per calcolare il logaritmo decimale o naturale di un numero positivo basta usare la calcolatrice scientifica.

LE EQUAZIONI LOGARITMICHE Un’equazione si dice logaritmica quando l’incognita compare come argomento di uno o più logaritmi. Poiché abbiamo visto che è possibile calcolare in R solo i logaritmi di numeri positivi, quando risolviamo un’equazione logaritmica dovremo fare attenzione nella determinazione del suo dominio: ogni argomento di logaritmo dovrà essere positivo.

Per risolvere un’equazione logaritmica dovremo seguire il seguente procedimento: individuare il dominio dell’equazione richiedendo che ogni argomento di logaritmo sia positivo; applicare le proprietà dei logaritmi fino ad ottenere un’equazione nella forma loga A(x) = loga B(x) oppure loga A(x) = b Dove A(x) e B(x) sono espressioni di variabile x, b è un numero reale, a si suppone positivo e diverso da 1; uguagliare gli argomenti dei logaritmi nel primo caso, porre cioè A(x) = B(x) Trasformare l’equazione nella forma esponenziale equivalente nel secondo caso: A(x) = ab.

Vediamo alcuni esempi: Determiniamo il dominio dell’equazione chiedendo che siano positivi gli argomenti dei logaritmi; dobbiamo risolvere il sistema: La soluzione del sistema è l’insieme dei valori di x tali che , quindi il dominio dell’equazione è: L’equazione si presenta già nella forma loga A(x) = loga B(x), basta quindi uguagliare gli argomenti: La soluzione è accettabile perché appartiene al dominio.

Determiniamo innanzitutto il dominio dell’equazione: Osserviamo poi che il termine 3 può essere visto come log 2 8; l’equazione quindi si trasforma nella seguente:

Applicando le proprietà dei logaritmi, possiamo scrivere l’equazione nella forma: Solamente la seconda soluzione appartiene al dominio, quindi S = {-8}. Avremmo potuto evitare di ottenere un’equazione frazionaria se, prima di applicare le proprietà dei logaritmi, avessimo trasportato da un membro all’altro I termini con segno negativo; in questo modo si sarebbe ottenuta un’equazione in cui compaiono solo operazioni di addizione fra logaritmi e quindi poi solo operazioni di moltiplicazione fra gli argomenti.

Prova a svolgere il seguente esercizio guidato: Il dominio dell’equazione è D = {x | x > 0}. Opera la sostituzione log x = t; ottieni l‘equazione …………. le cui soluzioni sono t = …………… v t = ………………… Operando la sostituzione inversa hai log x = …………. v log x = …………. . Da cui x = ……………. . v x = ………………