JML and Class Specifications Class invariant JML definitions

JML and Class Specifications • • Class invariant JML definitions Queue example Running JML in Eclipse

Review JML Language 1. JML specs are comments: /*@ …. @*/ 2. The Hoare triple {P} s 1; s 2; …; sn {Q} is written in JML/Java as: /*@ requires P ; ensures Q ; @*/ type method (parameters) { locals s 1; s 2; …; sn }

More JML

Class Specifications A class C is formally specified if: 1. Every constructor and public method M in the class has preconditions and postconditions, and 2. C has a special predicate called its class invariant INV which, for every object o in C, argument x and call o. M(x), must be true both before and after the call. Note: During a call, INV may temporarily become false. Why are we doing this? ? ? • Formal specifications provide a foundation for rigorous OO system design (e. g. , “design by contract”). • They enable static and dynamic assertion checking of an entire OO system. • They enable formal correctness proof of an OO system.

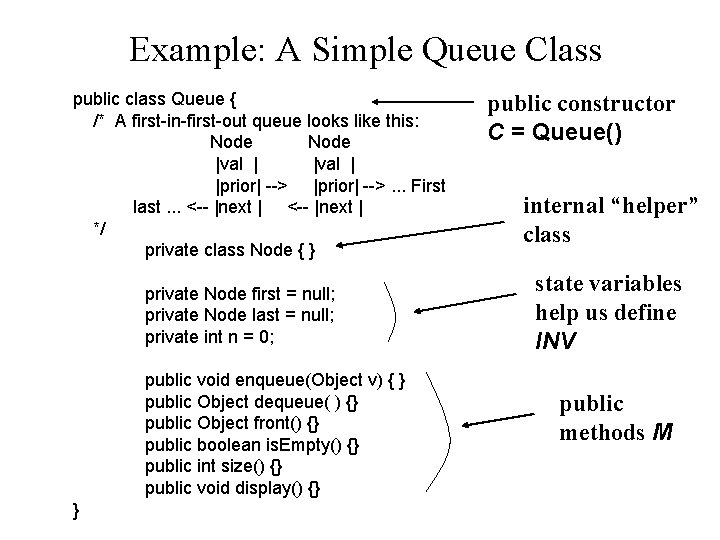
Example: A Simple Queue Class public class Queue { /* A first-in-first-out queue looks like this: Node |val | |prior| -->. . . First last. . . <-- |next | */ private class Node { } private Node first = null; private Node last = null; private int n = 0; public void enqueue(Object v) { } public Object dequeue( ) {} public Object front() {} public boolean is. Empty() {} public int size() {} public void display() {} } public constructor C = Queue() internal “helper” class state variables help us define INV public methods M

Adding Class-Level Specifications JML model variables /*@ public model Node H, T; private represents H <- first; class invariant INV private represents T <- last; public invariant n == size(); more JML @*/ private /*@ spec_public @*/ Node first = null; private /*@ spec_public @*/ Node last = null; private /*@ spec_public @*/ int n = 0; Notes: 1) JML model variables allow a specification to distance itself from the class’s implementation details. 2) “spec_public” allows JML specifications to treat a Java 3) variable as public without forcing the code to do the same.

Adding Method Specifications /*@ ensures T. prior == old(T) && H. prior == null && T. val. equals(v) ; @*/ public void enqueue(Object v) { last = new Node(v, last, null); if (first == null) first = last; else (last. prior). next = last; n = n+1; } Notes: 1) old denotes the value of T at entry to enqueue. 2) The ensures clause specifies that enqueue adds v to the 3) tail T, and that the head H is not affected.

What specifications for dequeue? /*@ @*/ public Object dequeue( ) { Object result = first. val; first = first. next; if (first != null) first. prior = null ; else last = null; n = n-1; return result; }

“Pure” methods /*@ requires n > 0; ensures result == H. val && H == old(H); @*/ public /*@ pure @*/ Object front() { return first. val; } Note: A method is pure if: 1) it has no non-local side effects, and 2) it is provably non-looping.

Design by Contract Concretized

The contract for the Queue class

Test driving the Queue class public class Queue. Test { public static void main(String[] args) { Queue q = new Queue(); int val; int n = Integer. parse. Int(args[0]); for (int i=1; i <= n; i++) q. enqueue(args[i]); System. out. print("Queue contents = "); q. display(); System. out. println("Is Queue empty? " + q. is. Empty()); System. out. println("Queue size = " + q. size()); while (! q. is. Empty()) { System. out. print(" dequeue " + q. dequeue()); System. out. print(" Queue contents = "); q. display(); } System. out. println("Is Queue empty now? " + q. is. Empty()); } }

Contract test 1: normal run % jmlrac Queue. Test 5 1 2 3 4 5 Queue contents = last --> 5 4 3 2 1 <-- first Is Queue empty? false Queue size = 5 dequeue 1 Queue contents = last --> 5 4 3 2 <-- first dequeue 2 Queue contents = last --> 5 4 3 <-- first dequeue 3 Queue contents = last --> 5 4 <-- first dequeue 4 Queue contents = last --> 5 <-- first dequeue 5 Queue contents = last --> <-- first Is Queue empty now? true %

Contract test 2: precondition violation Queue contents = last --> 1 2 3 4 5 <-- first … dequeue 4 Queue contents = last --> 5 <-- first dequeue 5 Queue contents = last --> <-- first Exception in thread "main" org. jmlspecs. jmlrac. runtime. JMLEntry. Precondition. Error: by method Queue. dequeue regarding specifications at File ". . /home/allen/Desktop/workspace/my. Queue. Test/myqueuetest/ Queue. java", line 36, character 29 when 'this' is myqueuetest. Queue@b 166 b 5 at myqueuetest. Queue. check. Pre$dequeue$Queue(Queue. java: 626) at myqueuetest. Queue. dequeue(Queue. java: 771) at myqueuetest. Queue. Test. main(Queue. Test. java: 16) Note: blame is likely to be with the caller Queue. Test, since a precondition has been violated.

Contract test 3: postcondition violation Queue contents = last --> 5 4 3 2 1 <-- first Is Queue empty? False Exception in thread "main" org. jmlspecs. jmlrac. runtime. JMLNormal. Postcondition. Error: by method Queue. dequeue regarding specifications at File ". . /home/allen/Desktop/workspace/ my. Queue. Test/myqueuetest/Queue. java", line 37, character 52 when 'old(H)' is myqueuetest. Queue$Node@b 166 b 5 'result' is 5 'this' is myqueuetest. Queue@cdfc 9 c … Note: blame is likely to be with the callee Queue, since a postcondition has been violated.

Contract test 4: invariant error % jmlrac Queue. Test 5 1 2 3 4 5 Exception in thread "main" org. jmlspecs. jmlrac. runtime. JMLInvariant. Error: by method Queue. enqueue@post<File ". . /home/allen/Desktop/workspace/ my. Queue. Test/myqueuetest/Queue. java", line 28, character 24> regarding specifications at File ". . /home/allen/Desktop/workspace/my. Queue. Test/ myqueuetest/Queue. java", line 22, character 38 … Note: blame is again likely to be with the callee Queue, since an invariant has been violated.

Class and System Correctness So far, we have only done testing! What about formal verification? 1. A class C is (formally) correct if: a. It is formally specified, and b. For every object o and every constructor and public method M in the class, the Hoare triple is valid for every argument x. 2. A system is correct if all its classes are correct.

E. g. , Correctness of dequeue() 1. 2. 3. 4. 5. 6. 7. /*@ requires n > 0; ensures result. equals(old(H). val) && H == old(H). next; @*/ public Object dequeue( ) { Object result = first. val; first = first. next; if (first != null) first. prior = null ; To prove: else last = null; n = n-1; where: return result; } Note: We again use rules of inference and reason through the code, just like we did with Factorial.

A “loose” correctness proof for dequeue() 1. “Loose” because a. We assume the validity of size(), and b. We omit some details. 2. The assignments in dequeue(), together with ensure the validity of : a. Steps 1 and 7 establish result = old(first). val b. Steps 2 -5 establish first = old(first). next c. Step 6 and our assumption establish n = size(): a. I. e. , n = old(n) -1 1. and size() = old(size()) -1 a. c. So, n = size(), since old(n) = old(size()) ,

More Observations 1. Formal verification: a. is an enormous task for large programs. b. only proves that specifications and code agree. c. only proves partial correctness (assumes termination). 2. Tools exist for: a. Statically checking certain run-time properties of Java programs (ESC/Java 2) b. formally verifying Ada programs (Spark) 3. Tools are being developed to help with formal verification of Java programs (Diacron, LOOP) 4. What is the cost/benefit of formal methods? ? ?