Jet Physics in Heavy Ion Collisions at the

Jet Physics in Heavy Ion Collisions at the LHC Andreas Morsch CERN QGP Meeting’ 06, VECC, Kolkata, India, February 5 -7 th 2006

Outline n Reconstructed jets versus leading particles at the LHC n Jet reconstruction n Jet structure analysis

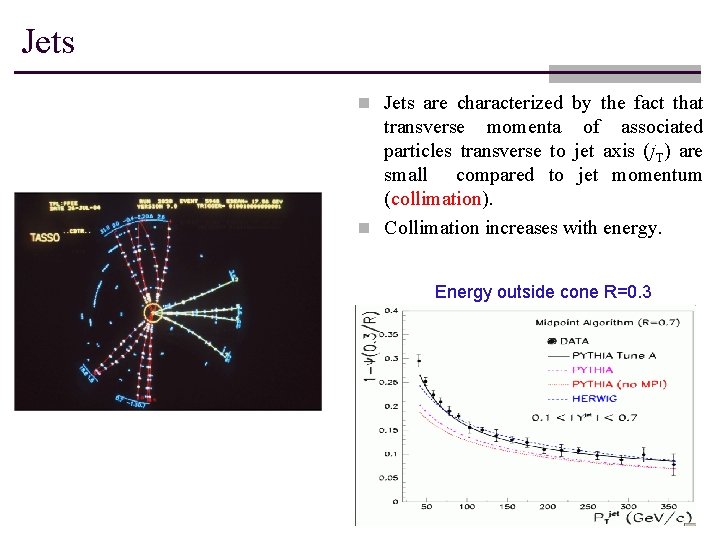
Jets n Jets are characterized by the fact that transverse momenta of associated particles transverse to jet axis (j. T) are small compared to jet momentum (collimation). n Collimation increases with energy. Energy outside cone R=0. 3

Jet Reconstruction: Full reconstruction n Jet finders, in general, n Uses collimated structure of the jet to find jet axis and subsequently maximizes energy inside a jet cone. n Jet cone in h-f: R = Dh 2+Df 2 n Typical jet cones 0. 7 -1 n 80% of jet energy in R < 0. 3 !

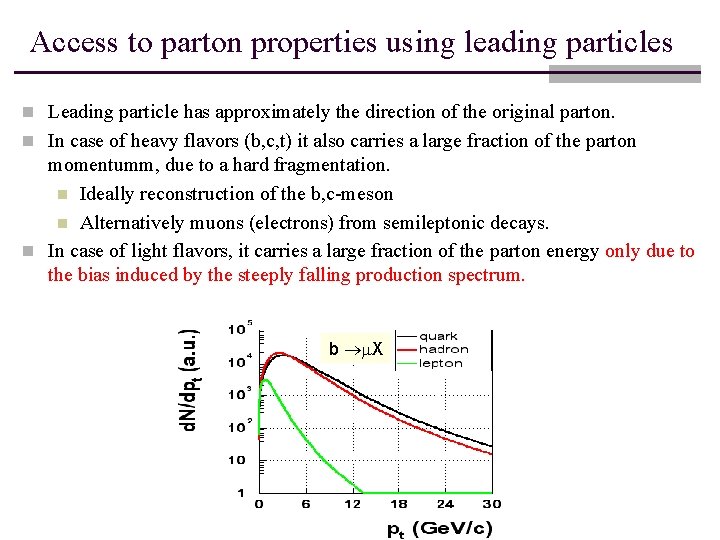
Access to parton properties using leading particles n Leading particle has approximately the direction of the original parton. n In case of heavy flavors (b, c, t) it also carries a large fraction of the parton momentumm, due to a hard fragmentation. n Ideally reconstruction of the b, c-meson n Alternatively muons (electrons) from semileptonic decays. n In case of light flavors, it carries a large fraction of the parton energy only due to the bias induced by the steeply falling production spectrum. b m. X

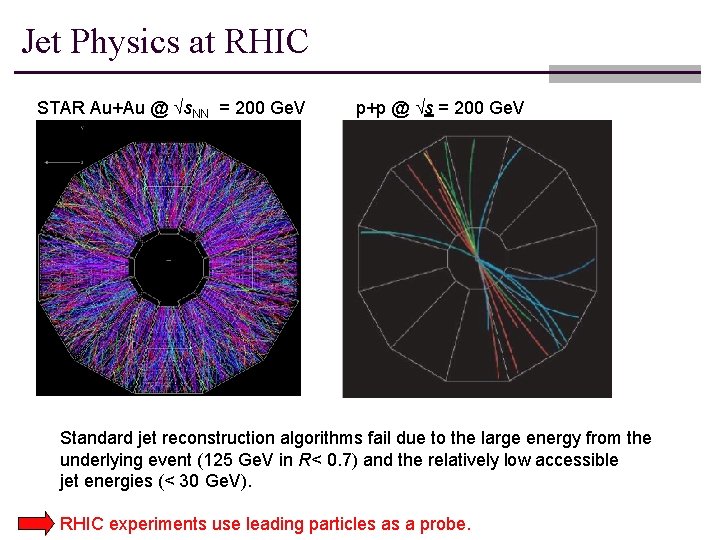
Jet Physics at RHIC STAR Au+Au @ s. NN = 200 Ge. V p+p @ s = 200 Ge. V Standard jet reconstruction algorithms fail due to the large energy from the underlying event (125 Ge. V in R< 0. 7) and the relatively low accessible jet energies (< 30 Ge. V). RHIC experiments use leading particles as a probe.

Quantities studied Hadron Suppression Similar RCP: Ratio central to peripheral p. T(assoc) “away side” Hadron Correlations: p. T(trig) – p. T(assoc) Df(trig, assoc) … “same side” p. T (trig)

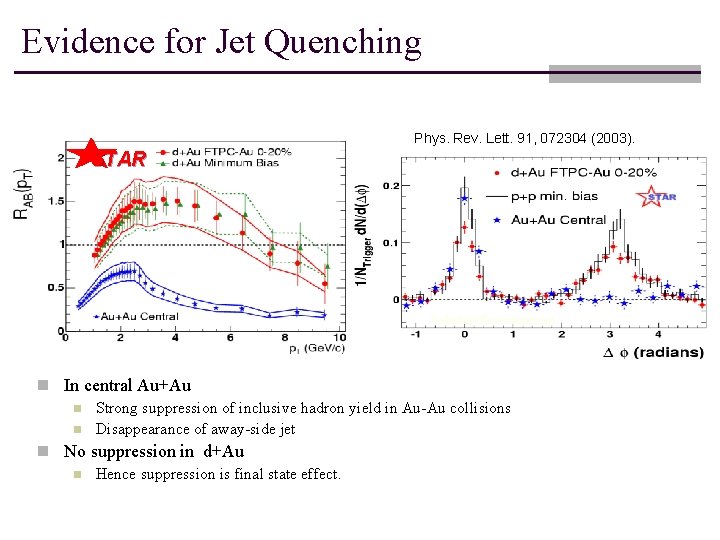
Evidence for Jet Quenching Phys. Rev. Lett. 91, 072304 (2003). STAR Pedestal&flow subtracted n In central Au+Au n Strong suppression of inclusive hadron yield in Au-Au collisions n Disappearance of away-side jet n No suppression in d+Au n Hence suppression is final state effect.

n Two good reasons for analyzing reconstructed jet instead of leading particles at high ET n n Bias on fragmentation function Efficiency

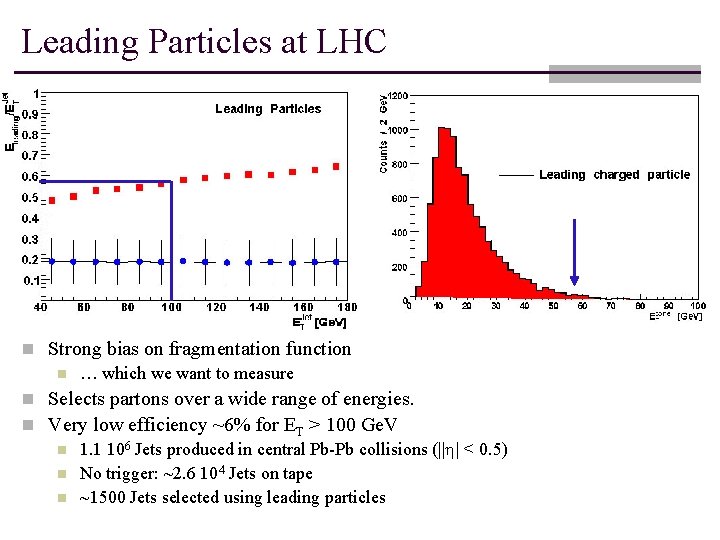
Leading Particles at LHC n Strong bias on fragmentation function n … which we want to measure n Selects partons over a wide range of energies. n Very low efficiency ~6% for ET > 100 Ge. V n 1. 1 106 Jets produced in central Pb-Pb collisions (||h| < 0. 5) n No trigger: ~2. 6 104 Jets on tape n ~1500 Jets selected using leading particles

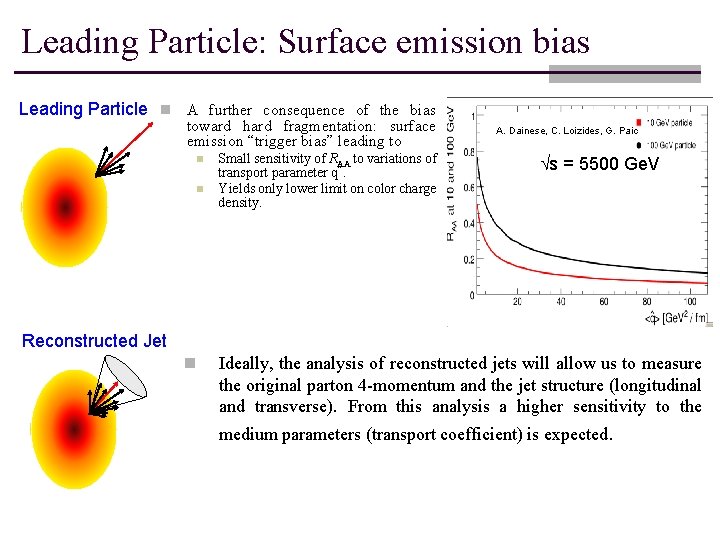
Leading Particle: Surface emission bias Leading Particle n A further consequence of the bias toward hard fragmentation: surface emission “trigger bias” leading to n n Small sensitivity of RAA to variations of transport parameter q^. Yields only lower limit on color charge density. A. Dainese, C. Loizides, G. Paic s = 5500 Ge. V Reconstructed Jet n Ideally, the analysis of reconstructed jets will allow us to measure the original parton 4 -momentum and the jet structure (longitudinal and transverse). From this analysis a higher sensitivity to the medium parameters (transport coefficient) is expected.

n What are the expected jet production rates at the LHC ? n Up to which energies do we have enough statistics for jet structure analysis ?

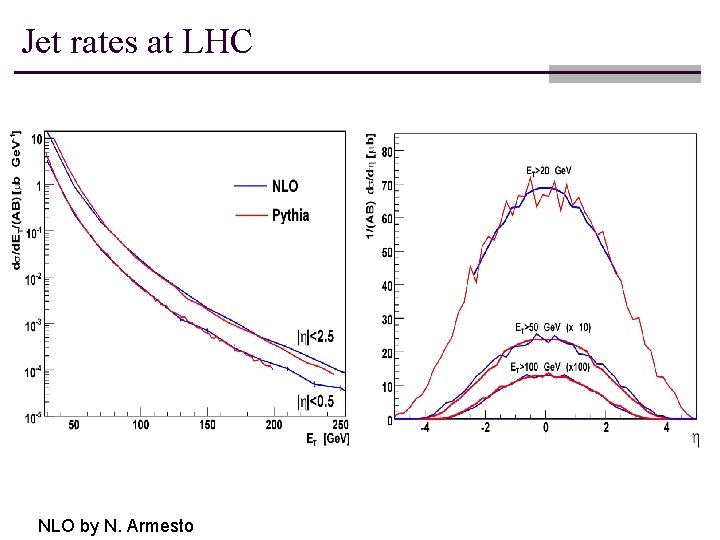
Jet rates at LHC NLO by N. Armesto

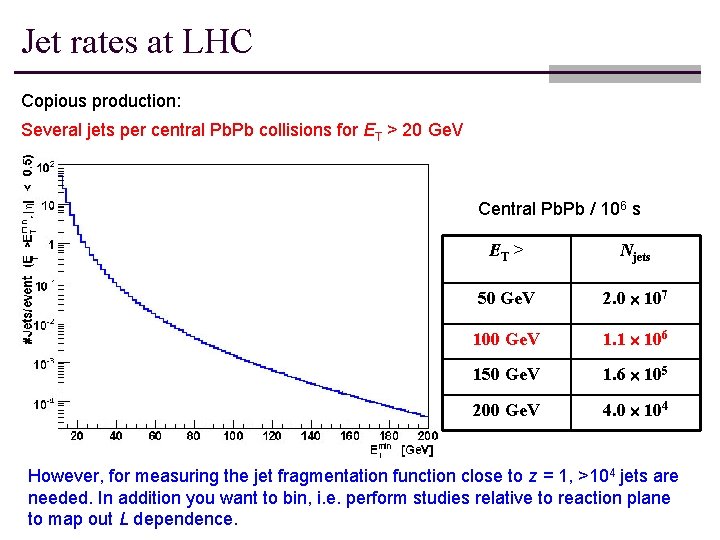
Jet rates at LHC Copious production: Several jets per central Pb. Pb collisions for ET > 20 Ge. V Central Pb. Pb / 106 s ET > Njets 50 Ge. V 2. 0 107 100 Ge. V 1. 1 106 150 Ge. V 1. 6 105 200 Ge. V 4. 0 104 However, for measuring the jet fragmentation function close to z = 1, >104 jets are needed. In addition you want to bin, i. e. perform studies relative to reaction plane to map out L dependence.

n How does the background from the underlying event limit jet reconstruction ? n n Need for smaller cone sizes and transverse momentum cuts. Incomplete reconstruction.

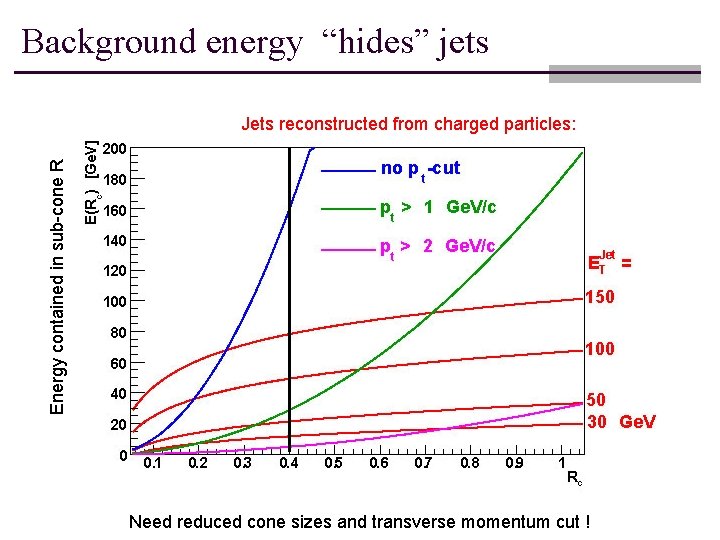
Jet identification n It has been shown (by embedding Pythia jets into HIJING) that even jets of moderate energies (ET > 50 Ge. V) can be identified over the huge background energy of the underlying HIJING event of central Pb. n Reasons: n n Collimation: Sizable fraction (~50%) of the jet energy is concentrated around jet axis (R< 0. 1). Background energy in cone of size R is ~ R 2 and background fluctuations ~ R. For d. Nch/dy = 5000: Energy in R = √(Dh 2+Df 2) < 0. 7: 1 Te. V !

Background energy “hides” jets Energy contained in sub-cone R Jets reconstructed from charged particles: Need reduced cone sizes and transverse momentum cut !

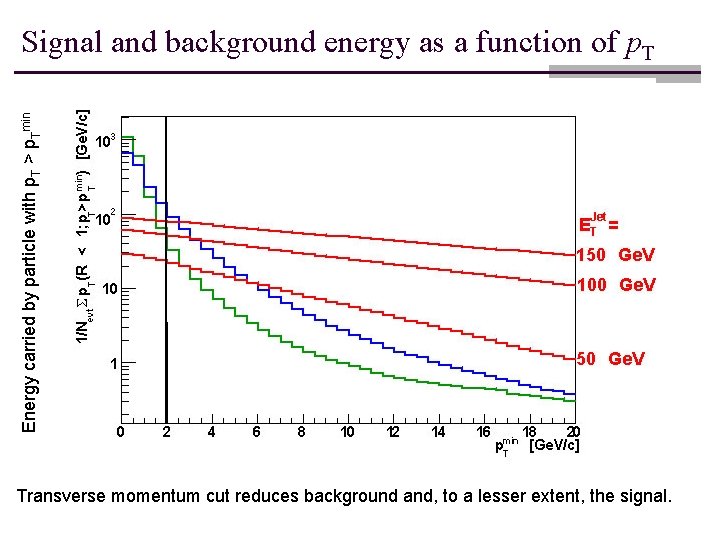
Energy carried by particle with p. T > p. Tmin Signal and background energy as a function of p. T Transverse momentum cut reduces background and, to a lesser extent, the signal.

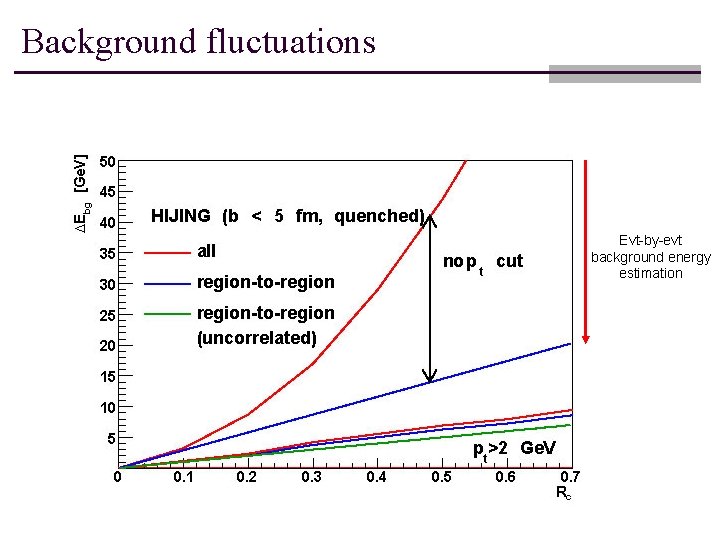
Background fluctuations limit resolution n Fluctuations caused by event-by-event variations of the impact parameter for a given centrality class. n n Strong correlation between different regions in h-f plane ~R 2 n Poissonian fluctuations of uncorrelated particles n n DE = N [<p. T>2 +sp. T 2] ~R n Correlated particles from common source (low-ET jets) n ~R

Background fluctuations Evt-by-evt background energy estimation

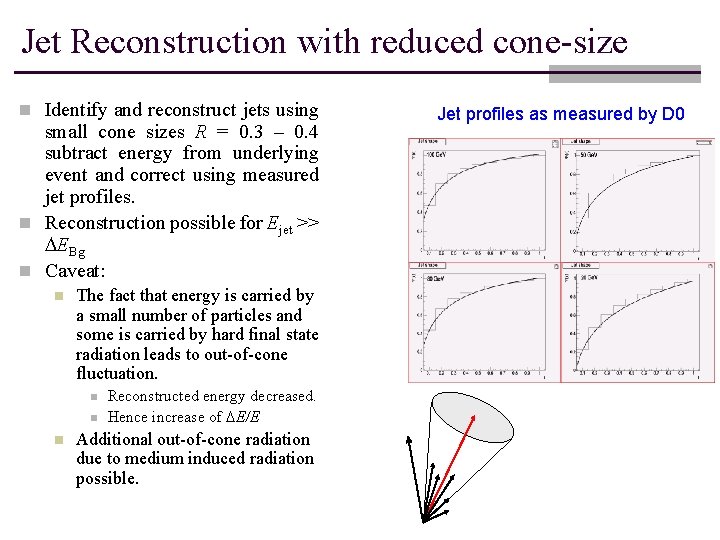
Jet Reconstruction with reduced cone-size n Identify and reconstruct jets using small cone sizes R = 0. 3 – 0. 4 subtract energy from underlying event and correct using measured jet profiles. n Reconstruction possible for Ejet >> DEBg n Caveat: n The fact that energy is carried by a small number of particles and some is carried by hard final state radiation leads to out-of-cone fluctuation. n n n Reconstructed energy decreased. Hence increase of DE/E Additional out-of-cone radiation due to medium induced radiation possible. Jet profiles as measured by D 0

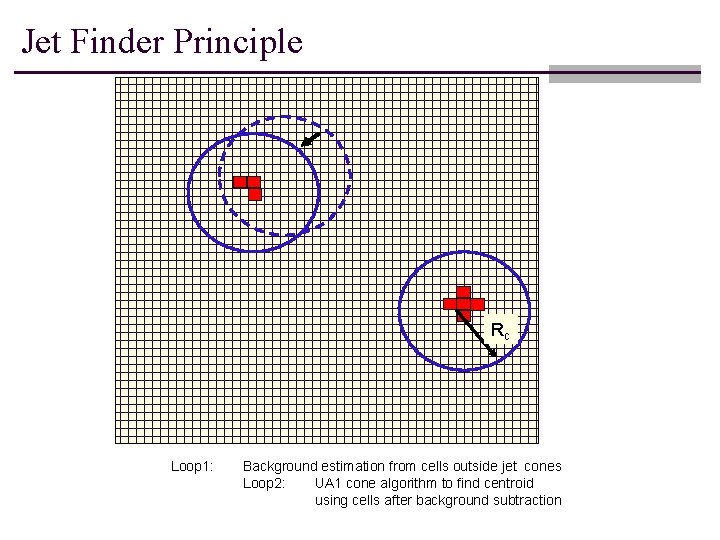
Jet Finder Principle Rc Loop 1: Background estimation from cells outside jet cones Loop 2: UA 1 cone algorithm to find centroid using cells after background subtraction

Jet Finder n Input: List of cells in an h-f grid sorted in decreasing cell energy Ei n Estimate the average background energy Ebg per cell from all cells. n For at least 2 iterations and until the change in Ebg between 2 successive iterations is smaller than a set threshold: n n n Clear the jet list Flag cells outside a jet. Execute the jet-finding loop for each cell, starting with the highest cell energy. If Ei – Ebg > Eseed and if the cell is not already flagged as being inside a jet: n n n Set the jet-cone centroid to be the center of the jet seed cell (hc, fc) = (hi, fi) Using all cells with (hi-h)2+(fi-f)2 < Rc of the initial centroid, calculate the new energy weighted centroid to be the new initial centroid. Repeat until difference between iterations shifts less than one cell. Store centroid as jet candidate. Recalculate background energy using information from cells outside jets.

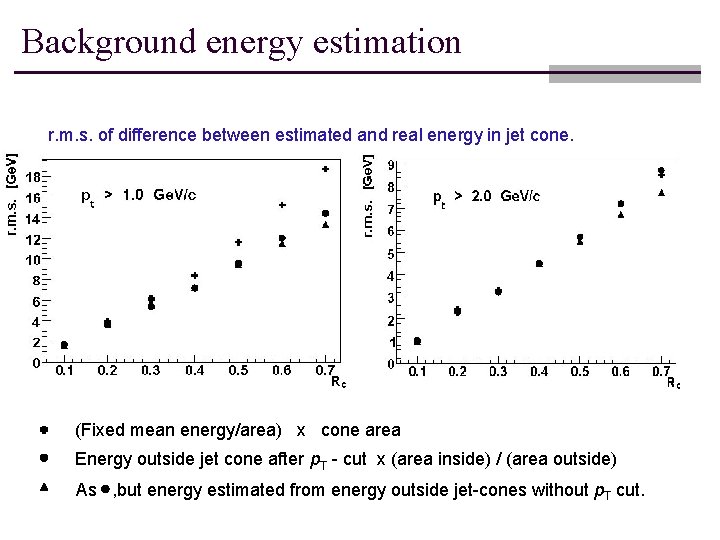
Background energy estimation r. m. s. of difference between estimated and real energy in jet cone. (Fixed mean energy/area) x cone area Energy outside jet cone after p. T - cut x (area inside) / (area outside) As , but energy estimated from energy outside jet-cones without p. T cut.

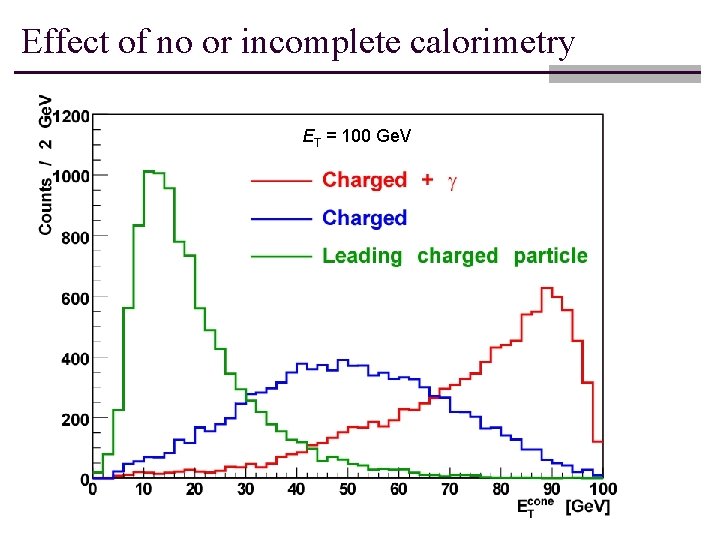
n Consequences of incomplete jet reconstruction: Signal fluctuations n n Charged jets: dominated by charged-to-neutral fluctuations Even with ideal calorimetry: out-of-cone fluctuations.

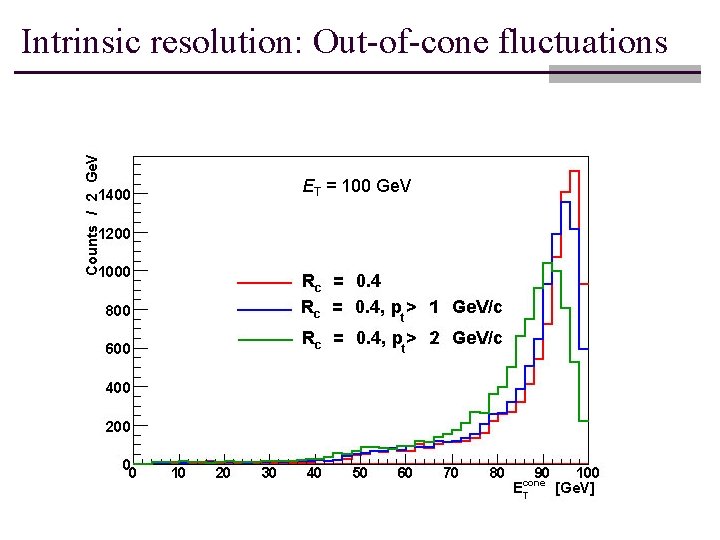
Intrinsic resolution: Out-of-cone fluctuations ET = 100 Ge. V

Effect of no or incomplete calorimetry ET = 100 Ge. V

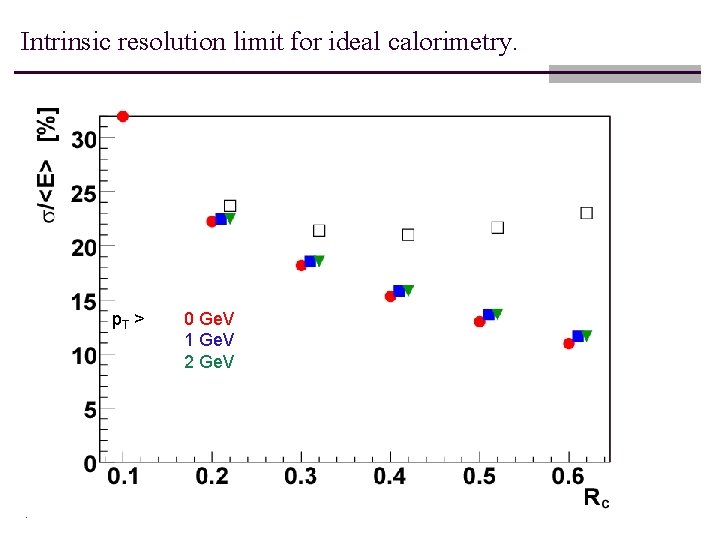
Intrinsic resolution limit for ideal calorimetry. p. T > 0 Ge. V 1 Ge. V 2 Ge. V

n So what do we gain with respect to leading particle analysis ? n n Reduced bias. Improved selectivity on parton energy.

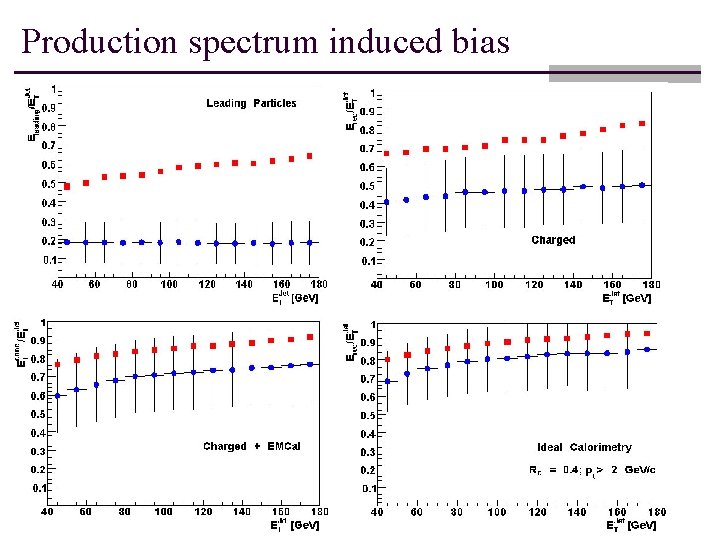
Production spectrum induced bias

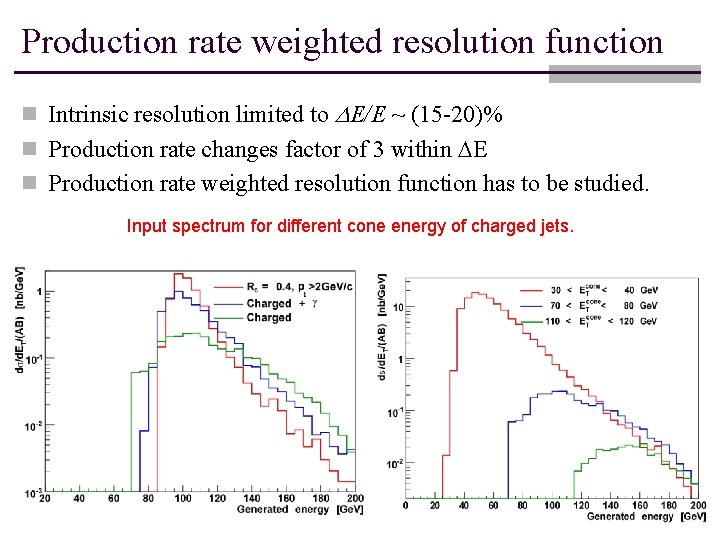
Production rate weighted resolution function n Intrinsic resolution limited to DE/E ~ (15 -20)% n Production rate changes factor of 3 within DE n Production rate weighted resolution function has to be studied. Input spectrum for different cone energy of charged jets.

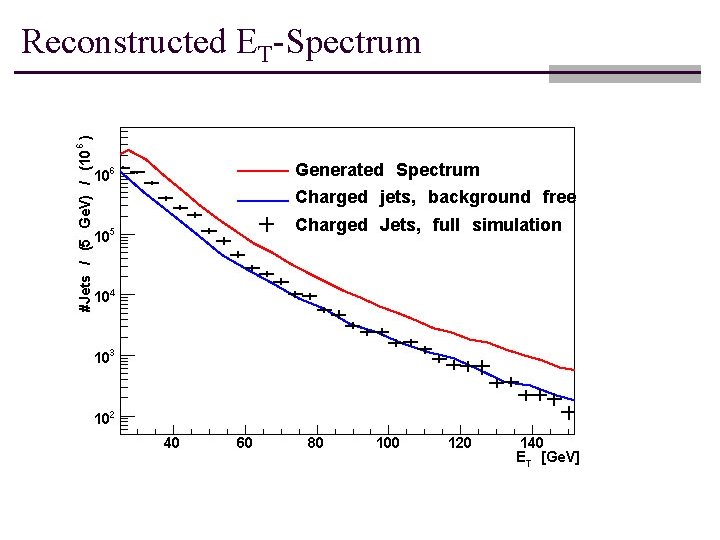
Reconstructed ET-Spectrum

Jet Structure Analysis

Transverse structure n Central question n Does the collimated structure of the jets survive so that they can be reconstructed event by event ? n n Study nuclear suppression factor RAAJet(ET, R) Total suppression (i. e. surface emission only) or do we reconstruct modified jets ? n Have the observed jets a modified transverse structure ? n n Measure jet shape d. E/d. R Measure momentum distribution perpendicular to the jet axis d. N/dj. T (“Transverse Heating”)

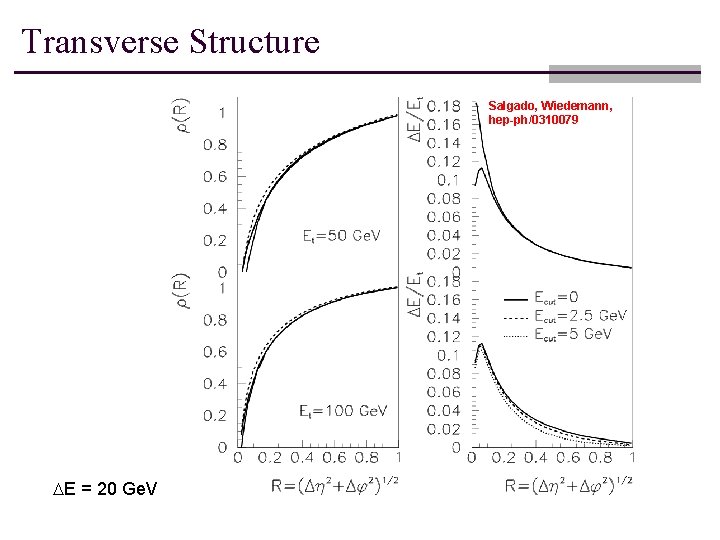
Transverse Structure Salgado, Wiedemann, hep-ph/0310079 DE = 20 Ge. V

Longitudinal structure n Measure parton energy as the energy of the reconstructed jet n Measure energy loss n Remnant of leading partons in the high-z part of the fragmentation function n Measure radiated energy n Additional low-z particles

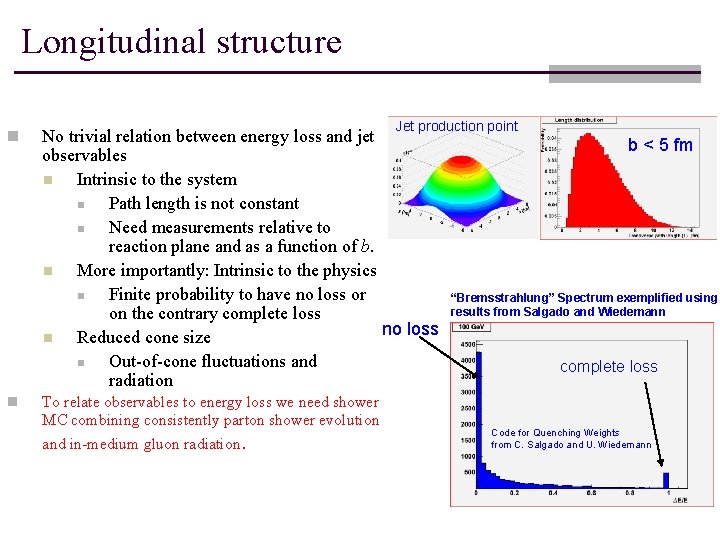
Longitudinal structure n n Jet production point No trivial relation between energy loss and jet observables n Intrinsic to the system n Path length is not constant n Need measurements relative to reaction plane and as a function of b. n More importantly: Intrinsic to the physics n Finite probability to have no loss or on the contrary complete loss no loss n Reduced cone size n Out-of-cone fluctuations and radiation To relate observables to energy loss we need shower MC combining consistently parton shower evolution and in-medium gluon radiation. b < 5 fm “Bremsstrahlung” Spectrum exemplified using results from Salgado and Wiedemann complete loss Code for Quenching Weights from C. Salgado and U. Wiedemann

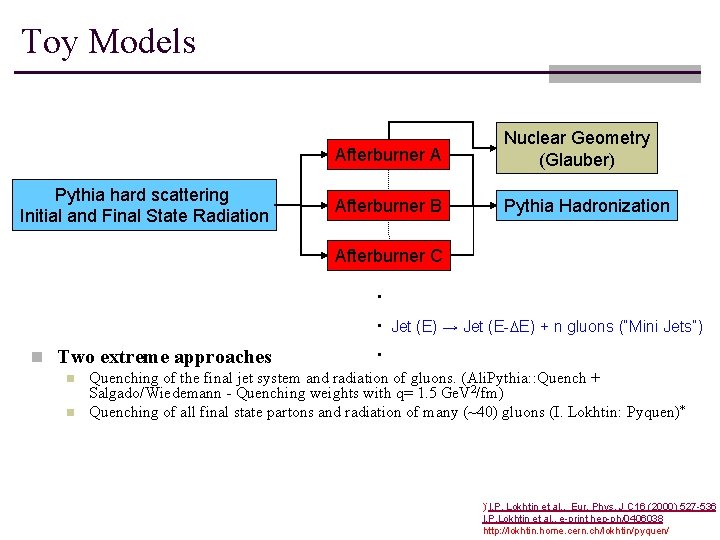
Toy Models Pythia hard scattering Initial and Final State Radiation Afterburner A Nuclear Geometry (Glauber) Afterburner B Pythia Hadronization Afterburner C n Two extreme approaches n n . . Jet (E) → Jet (E-DE) + n gluons (“Mini Jets”). Quenching of the final jet system and radiation of gluons. (Ali. Pythia: : Quench + Salgado/Wiedemann - Quenching weights with q= 1. 5 Ge. V 2/fm) Quenching of all final state partons and radiation of many (~40) gluons (I. Lokhtin: Pyquen)* )*I. P. Lokhtin et al. , Eur. Phys. J C 16 (2000) 527 -536 I. P. Lokhtin et al. , e-print hep-ph/0406038 http: //lokhtin. home. cern. ch/lokhtin/pyquen/

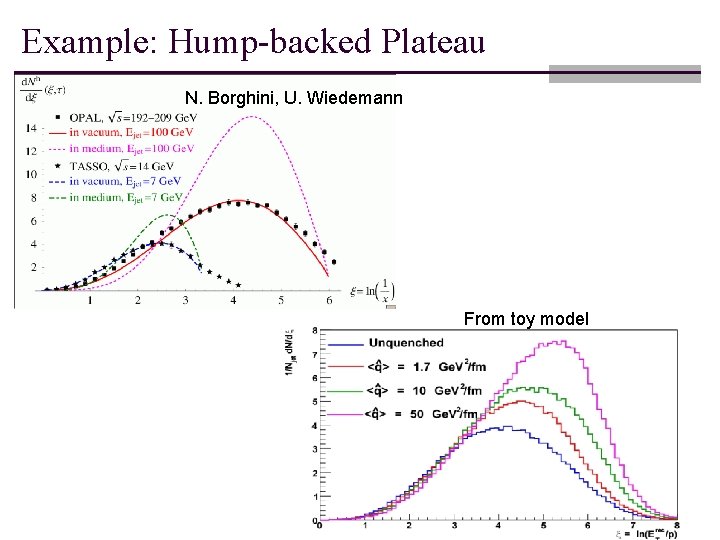
Example: Hump-backed Plateau N. Borghini, U. Wiedemann From toy model

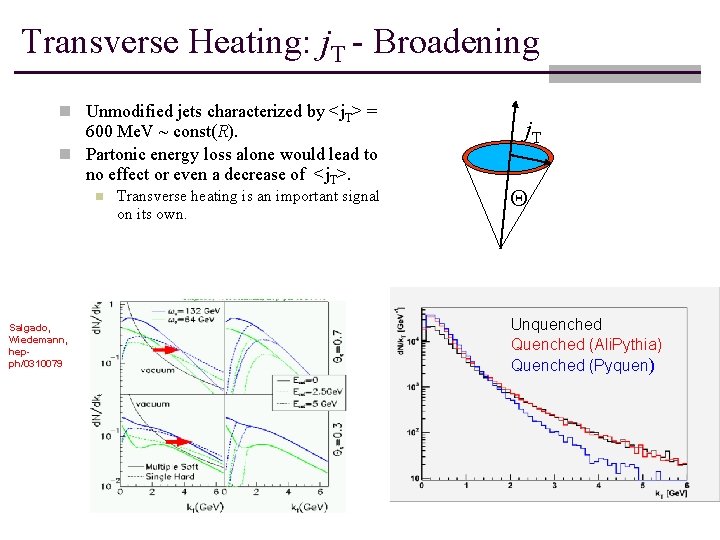
Transverse Heating: j. T - Broadening n Unmodified jets characterized by <j. T> = 600 Me. V ~ const(R). n Partonic energy loss alone would lead to no effect or even a decrease of <j. T>. n Salgado, Wiedemann, hepph/0310079 Transverse heating is an important signal on its own. j. T Q Unquenched Quenched (Ali. Pythia) Quenched (Pyquen)

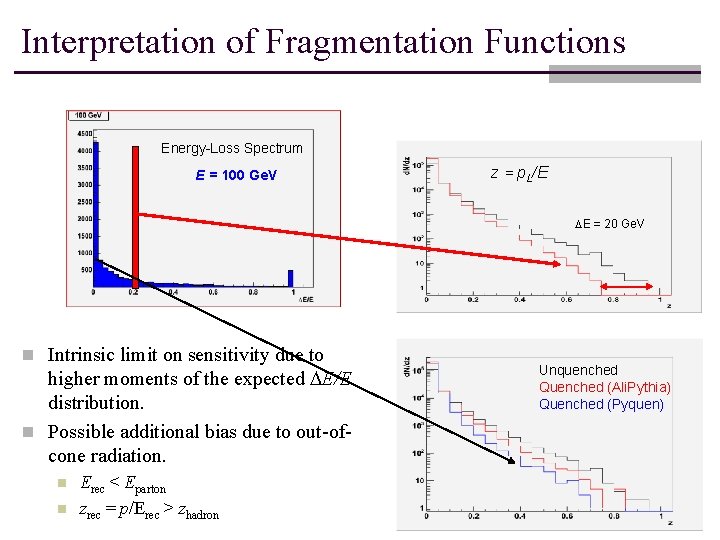
Interpretation of Fragmentation Functions Energy-Loss Spectrum E = 100 Ge. V z = p. L/E DE = 20 Ge. V n Intrinsic limit on sensitivity due to higher moments of the expected DE/E distribution. n Possible additional bias due to out-ofcone radiation. n n Erec < Eparton zrec = p/Erec > zhadron Unquenched Quenched (Ali. Pythia) Quenched (Pyquen)

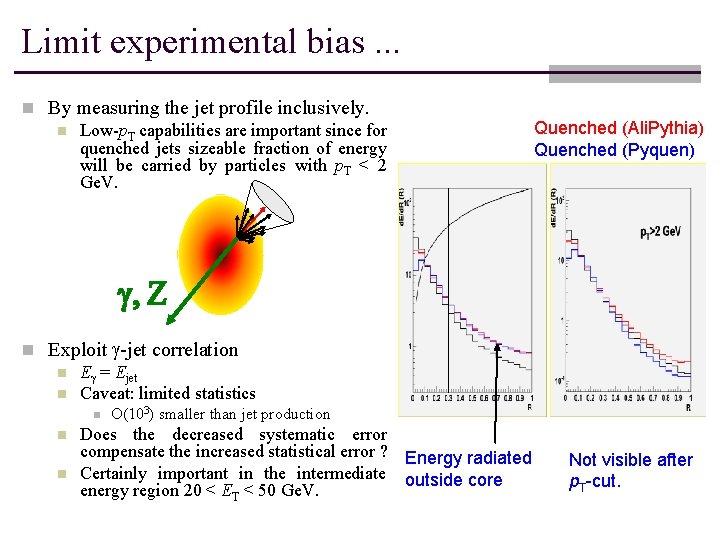
Limit experimental bias. . . n By measuring the jet profile inclusively. n Low-p. T capabilities are important since for quenched jets sizeable fraction of energy will be carried by particles with p. T < 2 Ge. V. Quenched (Ali. Pythia) Quenched (Pyquen) g, Z n Exploit g-jet correlation n Eg = Ejet n Caveat: limited statistics n n n O(103) smaller than jet production Does the decreased systematic error compensate the increased statistical error ? Energy radiated Certainly important in the intermediate outside core energy region 20 < ET < 50 Ge. V. Not visible after p. T-cut.

Role of background in jet structure analysis n Uncorrelated background particles n Bias due to incomplete reconstruction

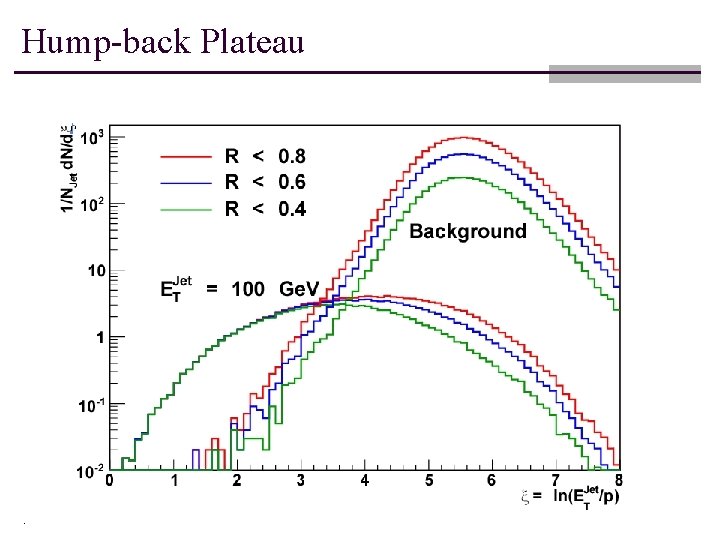
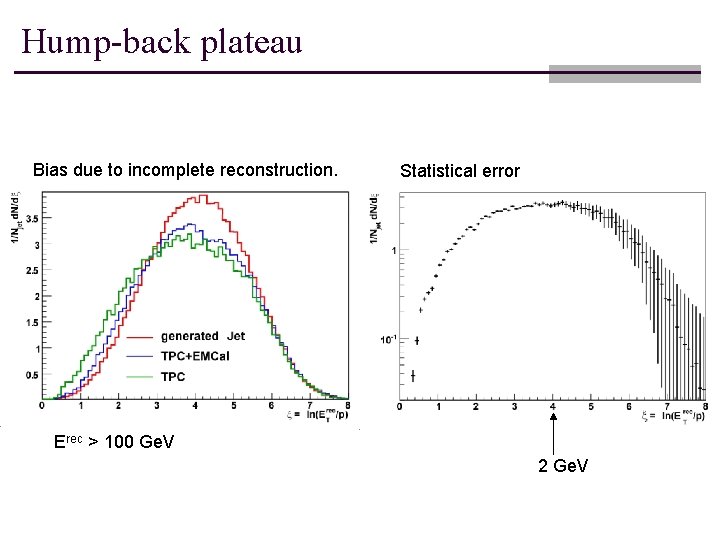
Hump-back Plateau

Hump-back plateau Bias due to incomplete reconstruction. Statistical error Erec > 100 Ge. V 2 Ge. V

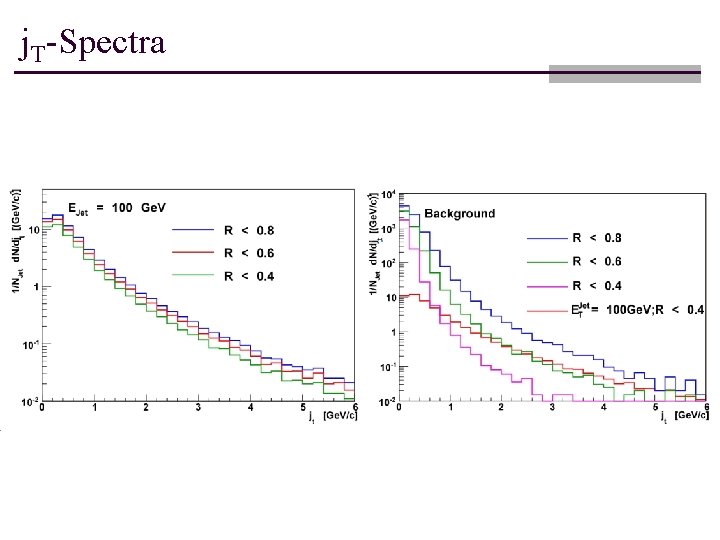
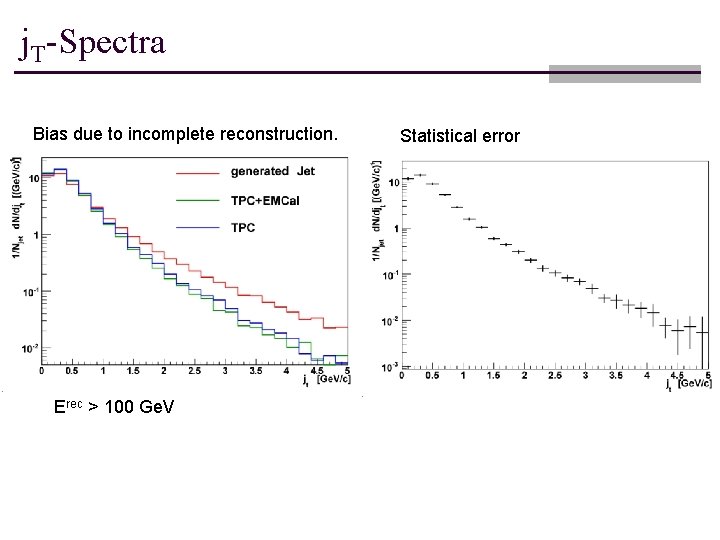
j. T-Spectra

j. T-Spectra Bias due to incomplete reconstruction. Erec > 100 Ge. V Statistical error

Conclusions n Copious production of jets in Pb. Pb collisions at the LHC n < 20 Ge. V many overlapping jets/event n Inclusive leading particle correlation n Background conditions require jet identification and reconstruction in reduced cone R < 0. 3 -0. 5 n At LHC we will measure jet structure observables (j. T, fragmentation function, jet-shape) for reconstructed jets. n High-p. T capabilities (calorimetry) needed to reconstruct parton energy n Good low-p. T capabilities are needed n n to measure particles from medium induced radiation. to reduce systematic bias from out-of-cone radiation n EMCal would add trigger capabilities and improve jet reconstruction n. . . and this would make it the ideal detector for jet physics at the LHC covering the needed low and high-p. T capabilities + particle ID.