JEHLAN Mgr Alena Tich Jehlan stecha stan tp




- Slides: 17

JEHLAN Mgr. Alena Tichá

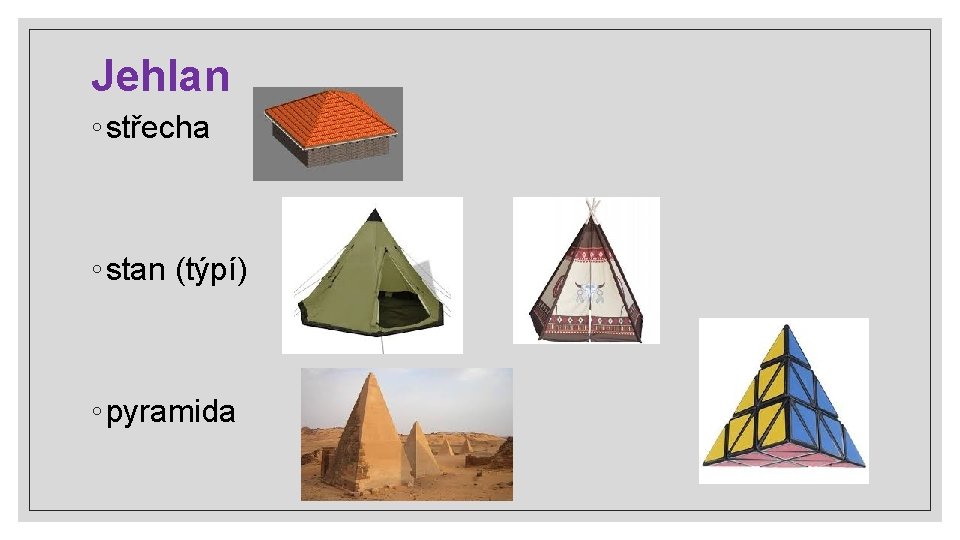
Jehlan ◦ střecha ◦ stan (týpí) ◦ pyramida

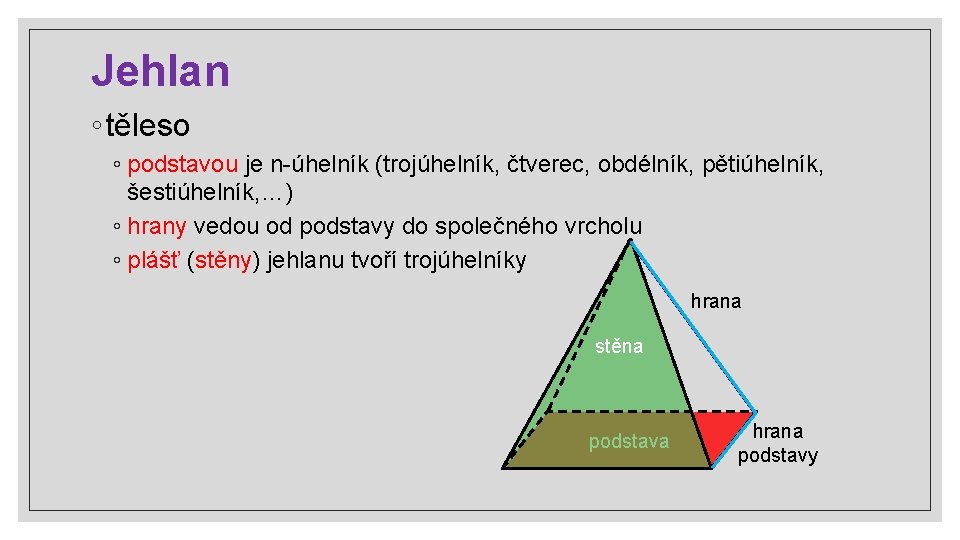
Jehlan ◦ těleso ◦ podstavou je n-úhelník (trojúhelník, čtverec, obdélník, pětiúhelník, šestiúhelník, …) ◦ hrany vedou od podstavy do společného vrcholu ◦ plášť (stěny) jehlanu tvoří trojúhelníky hrana stěna podstava hrana podstavy

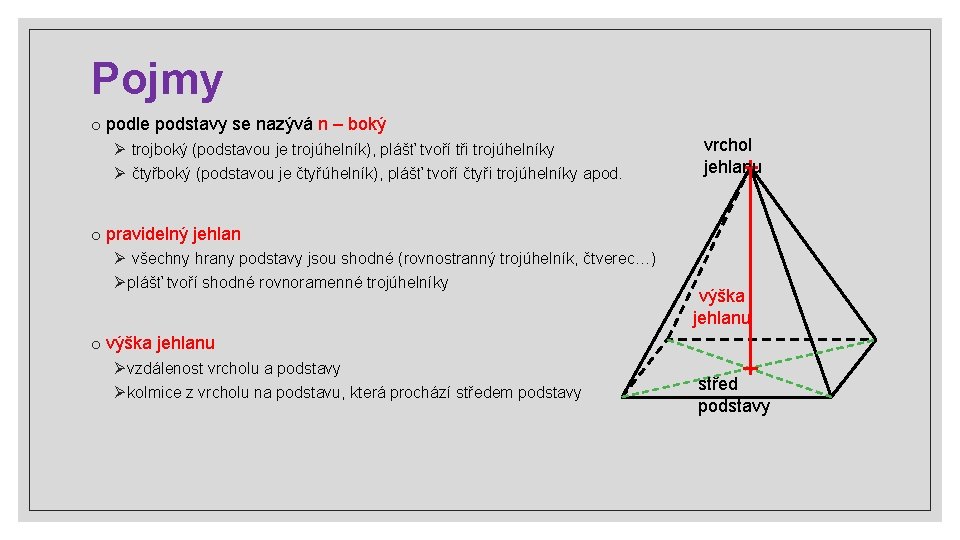
Pojmy o podle podstavy se nazývá n – boký Ø trojboký (podstavou je trojúhelník), plášť tvoří tři trojúhelníky Ø čtyřboký (podstavou je čtyřúhelník), plášť tvoří čtyři trojúhelníky apod. vrchol jehlanu o pravidelný jehlan Ø všechny hrany podstavy jsou shodné (rovnostranný trojúhelník, čtverec…) Ø plášť tvoří shodné rovnoramenné trojúhelníky výška jehlanu o výška jehlanu Ø vzdálenost vrcholu a podstavy Ø kolmice z vrcholu na podstavu, která prochází středem podstavy střed podstavy

Jak načrtnout jehlan? ◦ nejčastěji budeme pracovat se čtyřbokým jehlanem (podstavou je čtverec nebo obdélník) ◦ čárkovaně načrtneme podstavu – abychom docílili prostorového efektu, bude to kosočtverec nebo kosodélník ◦ pomocí úhlopříček si najdeme střed podstavy (také čárkovaně) ◦ ze středu svisle nahoru naznačíme výšku (a tedy i vrchol jehlanu) ◦ spojíme vrcholy podstavy a vrchol jehlanu ◦ plnými čarami obtáhneme viditelné hrany jehlanu ◦ je to náčrtek, takže nevadí, když to bude trochu křivé!!!

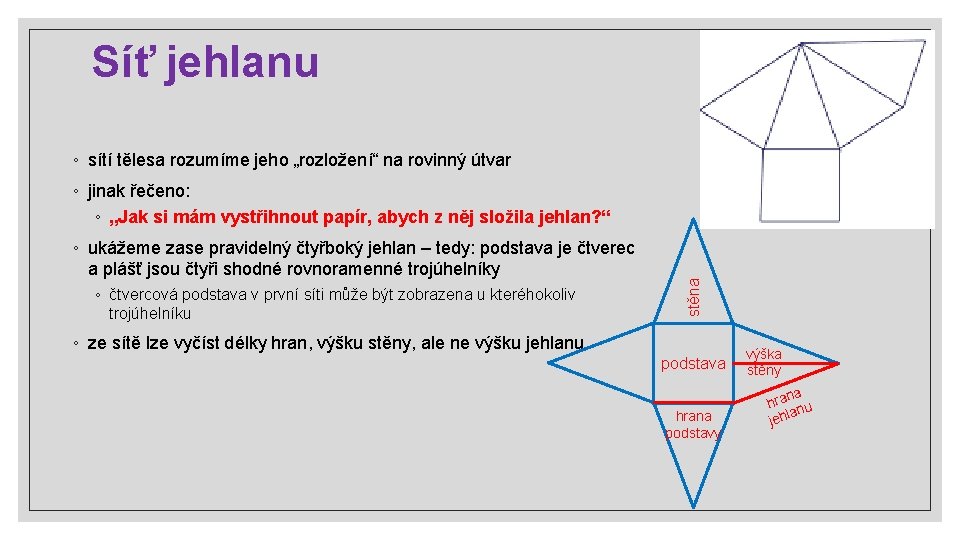
Síť jehlanu ◦ sítí tělesa rozumíme jeho „rozložení“ na rovinný útvar ◦ ukážeme zase pravidelný čtyřboký jehlan – tedy: podstava je čtverec a plášť jsou čtyři shodné rovnoramenné trojúhelníky ◦ čtvercová podstava v první síti může být zobrazena u kteréhokoliv trojúhelníku stěna ◦ jinak řečeno: ◦ „Jak si mám vystřihnout papír, abych z něj složila jehlan? “ ◦ ze sítě lze vyčíst délky hran, výšku stěny, ale ne výšku jehlanu podstava hrana podstavy výška stěny na a r h anu jehl

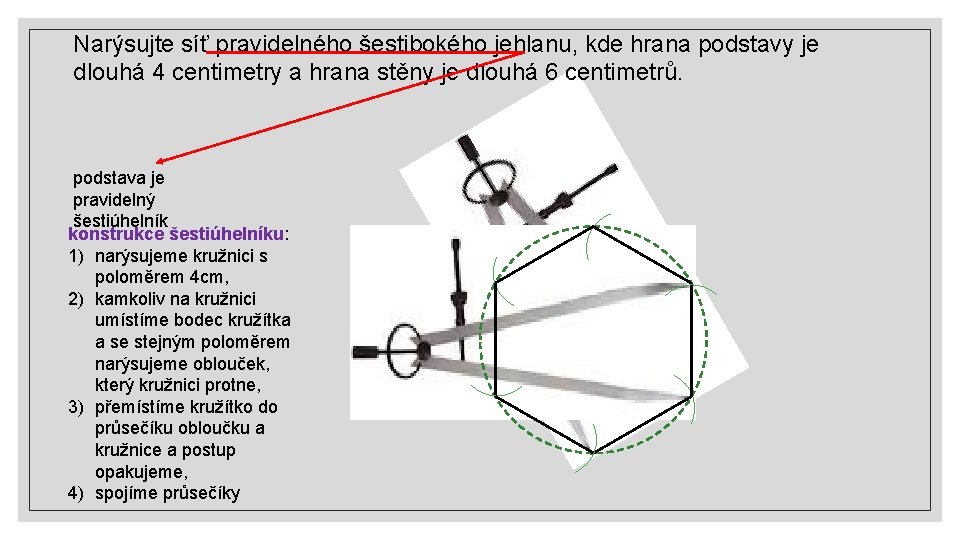
Narýsujte síť pravidelného šestibokého jehlanu, kde hrana podstavy je dlouhá 4 centimetry a hrana stěny je dlouhá 6 centimetrů. podstava je pravidelný šestiúhelník konstrukce šestiúhelníku: 1) narýsujeme kružnici s poloměrem 4 cm, 2) kamkoliv na kružnici umístíme bodec kružítka a se stejným poloměrem narýsujeme oblouček, který kružnici protne, 3) přemístíme kružítko do průsečíku obloučku a kružnice a postup opakujeme, 4) spojíme průsečíky

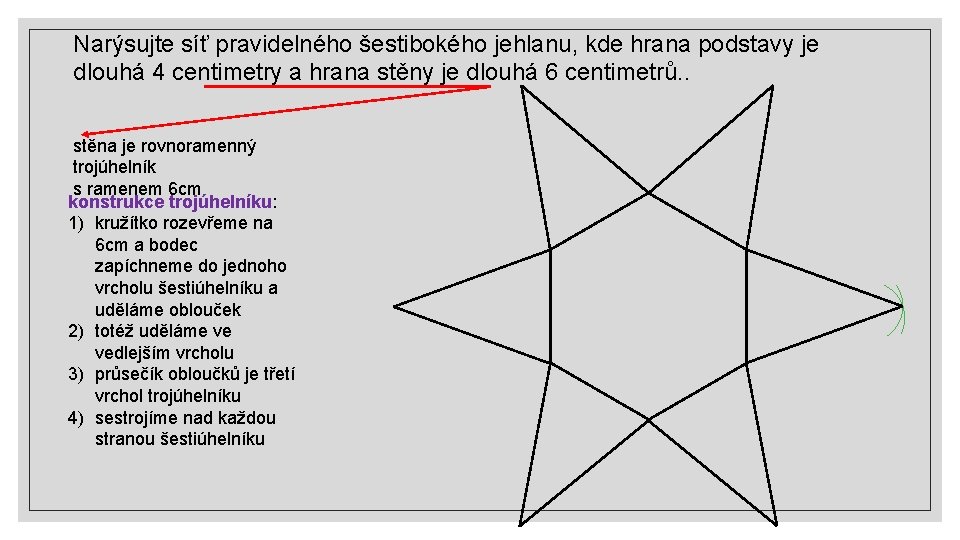
Narýsujte síť pravidelného šestibokého jehlanu, kde hrana podstavy je dlouhá 4 centimetry a hrana stěny je dlouhá 6 centimetrů. . stěna je rovnoramenný trojúhelník s ramenem 6 cm konstrukce trojúhelníku: 1) kružítko rozevřeme na 6 cm a bodec zapíchneme do jednoho vrcholu šestiúhelníku a uděláme oblouček 2) totéž uděláme ve vedlejším vrcholu 3) průsečík obloučků je třetí vrchol trojúhelníku 4) sestrojíme nad každou stranou šestiúhelníku

Objem a povrch tělesa ◦ objem tělesa udává množství „materiálu“, který by se vešel do tělesa ◦ značí se písmenem V a měří se v krychlových jednotkách nebo litrech ◦ m 3 – metr krychlový ◦ dm 3 – decimetr krychlový ◦ ml – mililitr ◦ l – litr ◦ povrch tělesa si můžeme představit jako množství materiálu, které spotřebujeme na jeho výrobu (nalakování, potažení látkou apod. ) ◦ je to zároveň obsah sítě tohoto tělesa ◦ značí se písmenem S a měří se ve čtverečních jednotkách ◦ m 2 – metr čtvereční ◦ cm 2 – centimetr čtvereční

Objem a povrch jehlanu ◦

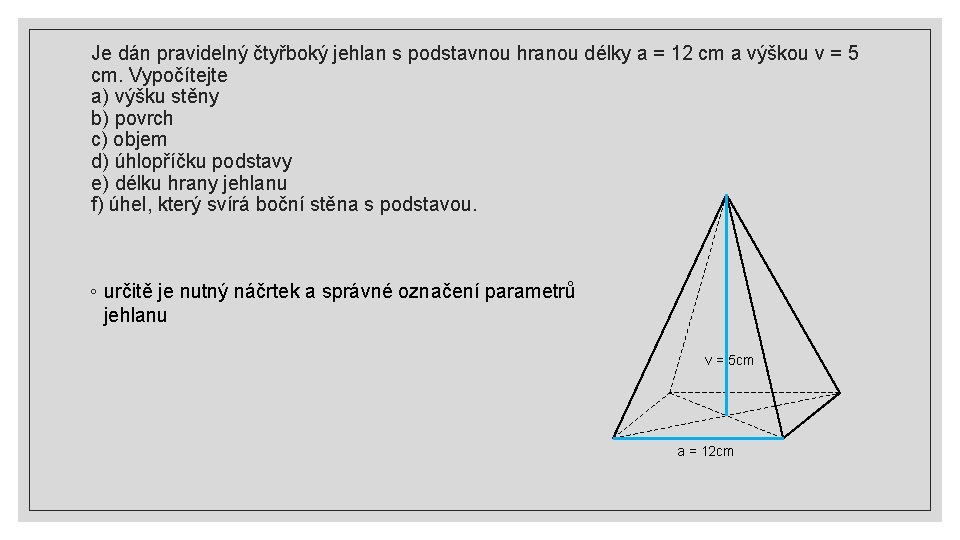
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte a) výšku stěny b) povrch c) objem d) úhlopříčku podstavy e) délku hrany jehlanu f) úhel, který svírá boční stěna s podstavou. ◦ určitě je nutný náčrtek a správné označení parametrů jehlanu v = 5 cm a = 12 cm

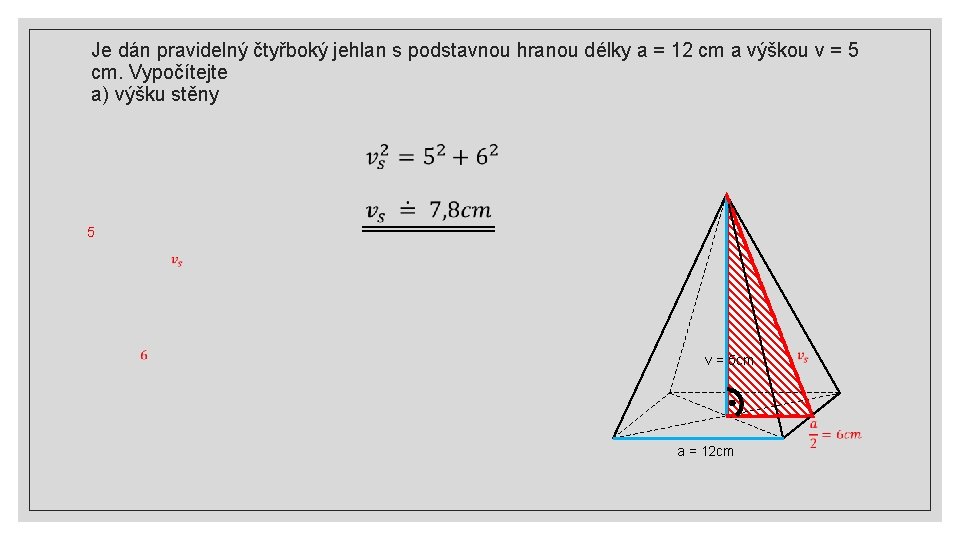
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte a) výšku stěny 5 v = 5 cm a = 12 cm

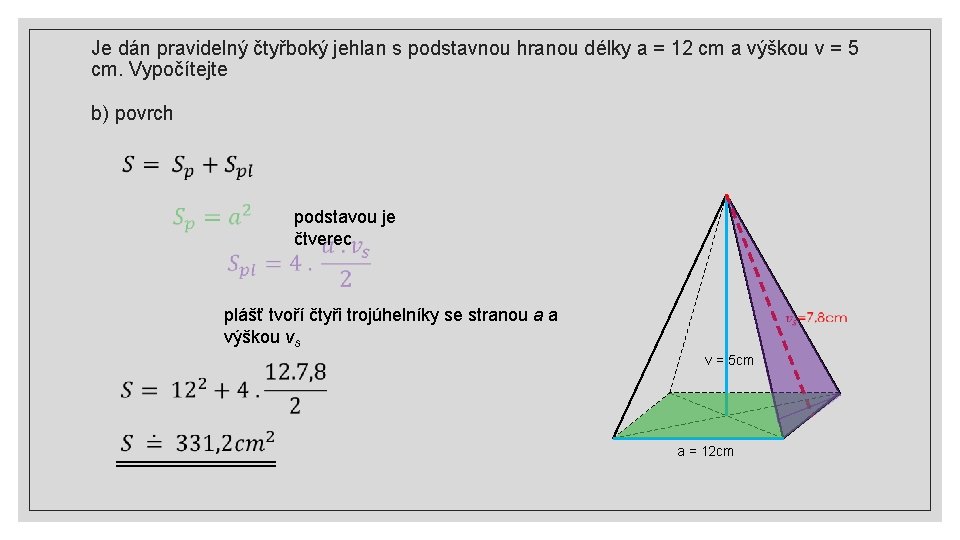
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte b) povrch podstavou je čtverec plášť tvoří čtyři trojúhelníky se stranou a a výškou vs v = 5 cm a = 12 cm

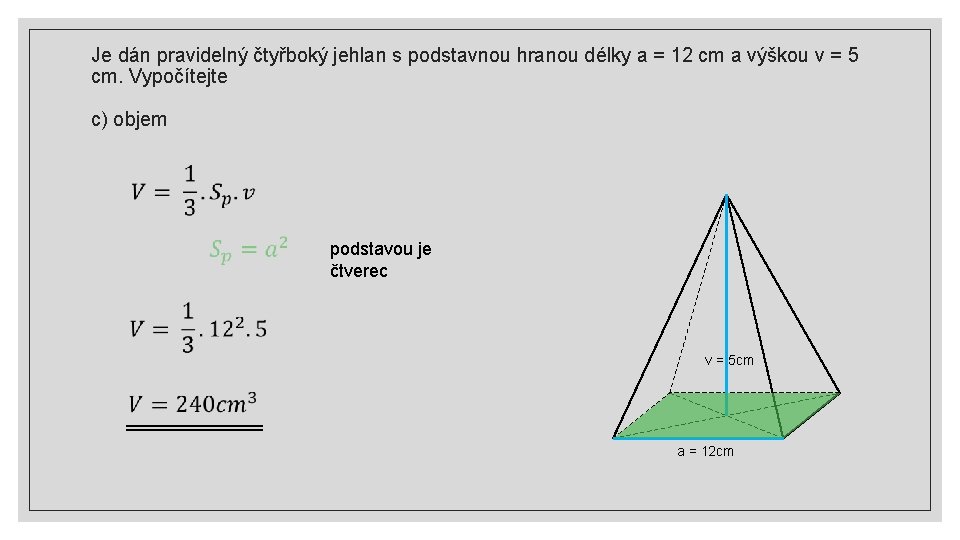
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte c) objem podstavou je čtverec v = 5 cm a = 12 cm

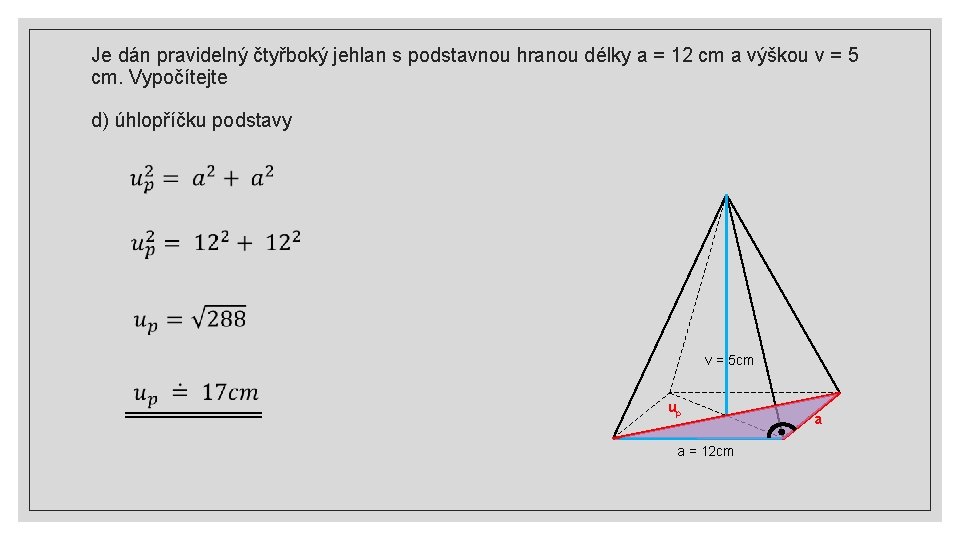
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte d) úhlopříčku podstavy v = 5 cm up a = 12 cm a

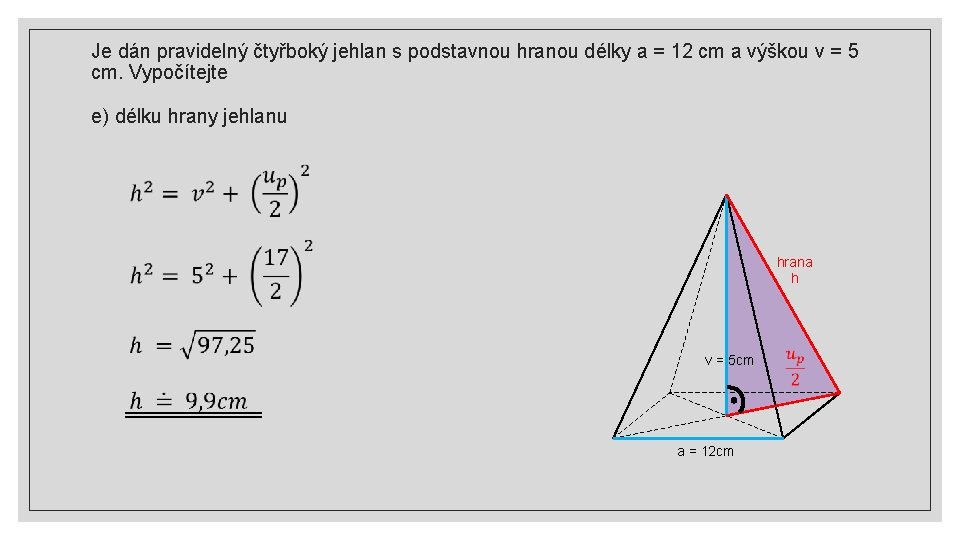
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte e) délku hrany jehlanu hrana h v = 5 cm a = 12 cm

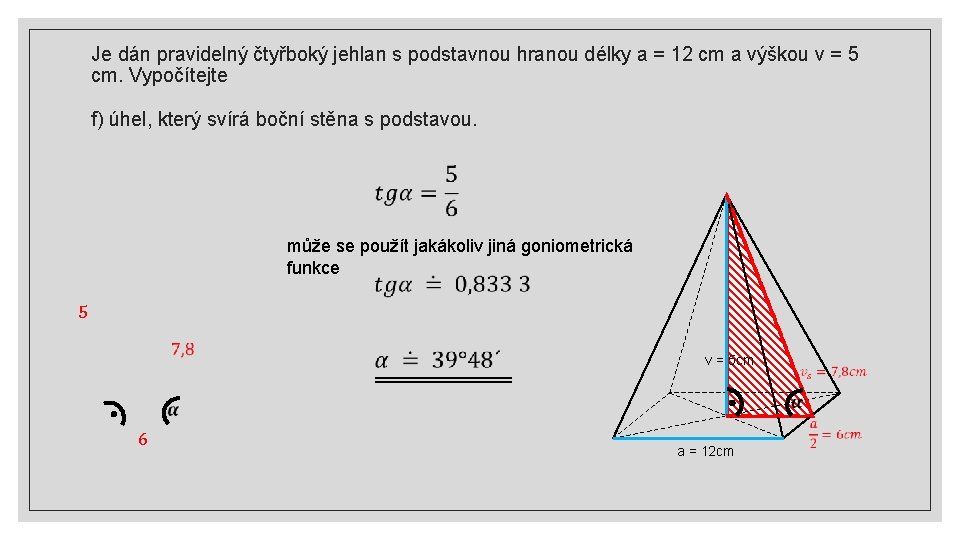
Je dán pravidelný čtyřboký jehlan s podstavnou hranou délky a = 12 cm a výškou v = 5 cm. Vypočítejte f) úhel, který svírá boční stěna s podstavou. může se použít jakákoliv jiná goniometrická funkce 5 v = 5 cm 6 a = 12 cm