Java Software Solutions Lewis and Loftus Recursion Introduction

Java Software Solutions Lewis and Loftus Recursion -- Introduction • Recursion is a fundamental programming technique that can provide an elegant solution certain kinds of problems • Chapter 12 focuses on: – – thinking in a recursive manner programming in a recursive manner the correct use of recursion examples 1

Java Software Solutions Lewis and Loftus Recursive Thinking • A recursive definition is one which uses the word or concept being defined in the definition itself • A recursive definition can be an appropriate way to express a concept • Before applying recursion to programming, it is best to practice thinking recursively 2

Java Software Solutions Lewis and Loftus Recursive Definitions • Consider the following list of numbers: 24, 88, 40, 37 • Such a list can be defined as A LIST is a: number or a: number comma LIST • That is, a LIST is defined to be a single number, or a number followed by a comma followed by a LIST • The concept of a LIST is used to define itself 3

Java Software Solutions Lewis and Loftus Recursive Definitions • The recursive part of the LIST definition is used several times, terminating with the non-recursive part: number comma LIST 24 , 88, 40, 37 number comma LIST 88 , 40, 37 number comma LIST 40 , 37 number 37 4

Java Software Solutions Lewis and Loftus Infinite Recursion • All recursive definitions have to have a nonrecursive part • If they didn't, there would be no way to terminate the recursive path • Such a definition would cause infinite recursion • This problem is similar to an infinite loop, but the non-terminating "loop" is part of the definition itself • The non-recursive part is often called the base case 5

Java Software Solutions Lewis and Loftus Recursive Definitions • N!, for any positive integer N, is defined to be the product of all integers between 1 and N inclusive • This definition can be expressed recursively as: 1! = 1 N! = N * (N-1)! • The concept of the factorial is defined in terms of another factorial • Eventually, the base case of 1! is reached 6

Java Software Solutions Lewis and Loftus Recursive Definitions 5! 120 5 * 4! 24 4 * 3! 6 3 * 2! 2 2 * 1! 1 7

Java Software Solutions Lewis and Loftus Recursive Programming • A method in Java can invoke itself; if set up that way, it is called a recursive method • The code of a recursive method must be structured to handle both the base case and the recursive case • Each call to the method sets up a new execution environment, with new parameters and local variables • As always, when the method completes, control returns to the method that invoked it (which may be an earlier invocation of itself) 8

Java Software Solutions Lewis and Loftus Recursive Programming • Consider the problem of computing the sum of all the numbers between 1 and any positive integer N • This problem can be recursively defined as: N N-1 = N i=1 = + N-2 = i=1 N + (N-1) + i=1 etc. • See Recursive_Sum. java 9

Java Software Solutions Lewis and Loftus Example: Recursive_Sum. java class Recursive_Sum { public static void main (String[] args) { System. out. println ("The sum of 1 to 3 is " + sum (3)); System. out. println ("The sum of 1 to 6 is " + sum (6)); System. out. println ("The sum of 1 to 10 is " + sum (10)); System. out. println ("The sum of 1 to 15 is " + sum (15)); } // method main public static int sum (int N) { int result; if (N == 1) result = 1; else result = N + sum (N-1); return result; } // method sum } // class Recursive_Sum Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 10

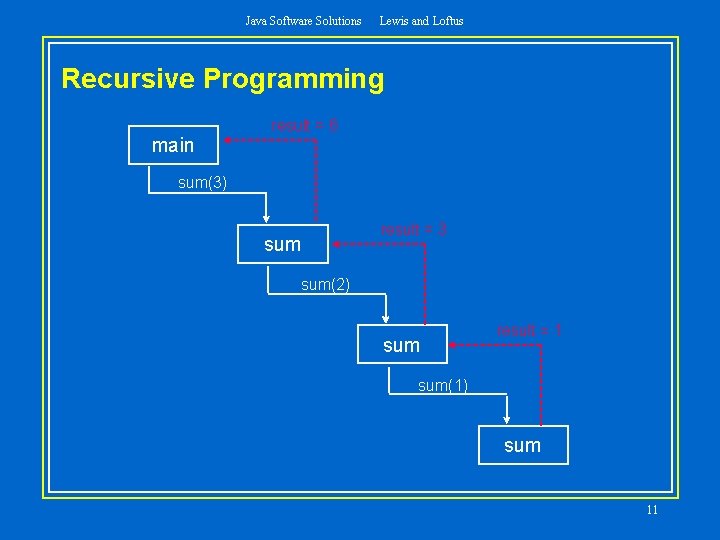
Java Software Solutions Lewis and Loftus Recursive Programming main result = 6 sum(3) sum result = 3 sum(2) sum result = 1 sum(1) sum 11

Java Software Solutions Lewis and Loftus Recursive Programming • Note that just because we can use recursion to solve a problem, doesn't mean we should • For instance, we usually would not use recursion to solve the sum of 1 to N problem, because the iterative version is easier to understand • However, for some problems, recursion provides an elegant solution, often cleaner than an iterative version • You must carefully decide whether recursion is the correct technique for any problem 12

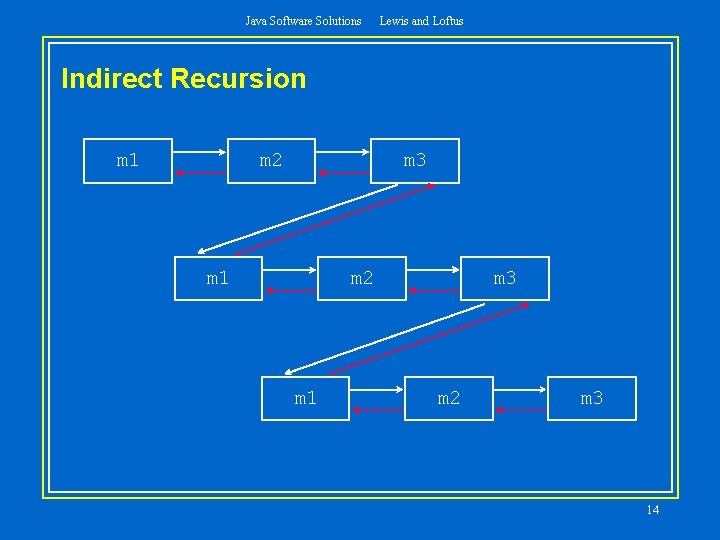
Java Software Solutions Lewis and Loftus Indirect Recursion • A method invoking itself is considered to be direct recursion • A method could invoke another method, which invokes another, etc. , until eventually the original method is invoked again • For example, method m 1 could invoke m 2, which invokes m 3, which in turn invokes m 1 again • This is called indirect recursion, and requires all the same care as direct recursion • It is often more difficult to trace and debug 13

Java Software Solutions Lewis and Loftus Indirect Recursion m 1 m 2 m 3 m 1 m 2 m 1 m 3 m 2 m 3 14

Java Software Solutions Lewis and Loftus Using Recursion • Recursion is best served when it is easy to define a smaller subset of the problem in terms of the original • Consider the task of repeatedly displaying a set of images in a mosaic that is reminiscent of looking in two mirrors reflecting each other • The base case is reached when the area for the images shrinks to a certain size • See Repeating_Pictures. java 15

Java Software Solutions Lewis and Loftus Example: Repeating_Pictures import java. applet. Applet; import java. awt. *; public class Repeating_Pictures extends Applet { private final int SIZE = 300; // Size of applet private final int STOP = 20; // Smallest picture size private final int OFFSET = 2; // Picture offset from lines private Image world; private Image everest; private Image goat; public void init() { world = get. Image (get. Document. Base(), "world. gif"); everest = get. Image (get. Document. Base(), "everest. gif"); goat = get. Image (get. Document. Base(), "goat. gif"); set. Size (SIZE, SIZE); } 12// method init Chapter Copyright 1997 by John Lewis and William Loftus. All rights reserved. 16

Java Software Solutions Lewis and Loftus // Draws the entire picture recursively. public void draw_pictures (int size, Graphics page) { // Draw lines to create four quadrants page. draw. Line (size/2, 0, size/2, size); // vertical page. draw. Line (0, size/2, size/2); // horizontal // Draw three images in different quadrants page. draw. Image (world, 0+OFFSET, size/2 -(OFFSET*2), this); page. draw. Image (everest, size/2+OFFSET, 0+OFFSET, size/2 -(OFFSET*2), this); page. draw. Image (goat, size/2+OFFSET, size/2 -(OFFSET*2), this); // Draw the entire picture again in the first quadrant if (size > STOP) draw_pictures (size/2, page); } // method draw_pictures // Performs the initial call to the draw_pictures method. public void paint (Graphics page) { draw_pictures (get. Size(). width, page); } // method paint } // class Repeating_Pictures Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 17

Java Software Solutions Lewis and Loftus Using Recursion • A palindrome is a string of characters that reads the same forward and backward: – radar – able was I ere I saw elba • To determine whether a string is a palindrome, you can examine the two outer characters, and work your way in toward the middle of the string • This solution is easily defined recursively • See Palindromes. java 18

Java Software Solutions Lewis and Loftus Example: Palindromes. java public class Palindromes { // Creates a Palindrome_Tester object, and tests several strings. public static void main (String[] args) { Palindrome_Tester tester = new Palindrome_Tester(); System. out. println ("radar is a palindrome? " + tester. ptest ("radar")); System. out. println ("abcddcba is a palindrome? " + tester. ptest ("abcddcba")); System. out. println ("able was I ere I saw elba is a palindrome? " + tester. ptest ("able was I ere I saw elba")); System. out. println ("hello is a palindrome? " + tester. ptest ("hello")); System. out. println ("abcxycba is a palindrome? " + tester. ptest ("abcxycba")); } // method main } // class Palindromes Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 19

Java Software Solutions Lewis and Loftus Example: Palindromes class Palindrome_Tester { // Uses recursion to perform the palindrome test. public boolean ptest (String str) { boolean result = false; if (str. length() <= 1) result = true; else if (str. char. At (0) == str. char. At (str. length()-1)) result = ptest (str. substring (1, str. length()-1)); return result; } // method ptest } // class Palindrome_Tester Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 20

Java Software Solutions Lewis and Loftus Using Recursion • A maze is solved by trial and error -- choosing a direction, following a path, returning to a previous point if the wrong move is made • As such, it is another good candidate for a recursive solution • The base case is an invalid move or one which reaches the final destination • See Maze_Search. java 21

Java Software Solutions Lewis and Loftus Example: Maze_Search. java public class Maze_Search { // Creates a new maze, prints its original form, attempts // to solve it, and prints out its final form. public static void main (String[] args) { Maze labyrinth = new Maze(); labyrinth. print_maze(); if (labyrinth. solve(0, 0)) System. out. println ("Maze solved!"); else System. out. println ("No solution. "); labyrinth. print_maze(); } // method main } // class Maze_Search Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 22

Java Software Solutions Lewis and Loftus class Maze { int[][] grid = {{1, 1, 1, 0, 0, 0, 1, 1}, {1, 0, 1, 1, 0, 0, 1}, {0, 0, 1, 0, 0}, {1, 1, 1, 0, 1, 1, 1}, {1, 0, 0, 1, 1, 1, 0, 0, 1}, {1, 0, 1, 1, 1, 0, 1, 1}, {1, 0, 0, 0, 0}, {1, 1, 1, 1}}; // Prints the maze grid. public void print_maze () { System. out. println(); for (int row=0; row < grid. length; row++) { for (int column=0; column < grid[row]. length; column++) System. out. print (grid[row][column]); System. out. println(); } // method print_maze 23 Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved.

Java Software Solutions Lewis and Loftus // Attempts to recursively traverse the maze. . public boolean solve (int row, int column) { boolean done = false; if (valid (row, column)) { grid[row][column] = 3; // cell has been tried if (row == grid. length-1 && column == grid[0]. length-1) done = true; // maze is solved else { done = solve (row+1, column); // down if (!done) done = solve (row, column+1); // right if (!done) done = solve (row-1, column); // up if (!done) done = solve (row, column-1); // left } if (done) // part of the final path grid[row][column] = 7; } return done; } // method solve Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 24

Java Software Solutions Lewis and Loftus // Determines if a specific location is valid. private boolean valid (int row, int column) { boolean result = false; // check if cell is in the bounds of the matrix if (row >= 0 && row < grid. length && column >= 0 && column < grid[0]. length) // check if cell is not blocked and not previously tried if (grid[row][column] == 1) result = true; return result; } // method valid } // class Maze Chapter 12 Copyright 1997 by John Lewis and William Loftus. All rights reserved. 25