Java Programming Guided Learning with Early Objects Chapter

Java Programming: Guided Learning with Early Objects Chapter 11 Recursion

Objectives • Learn about recursive definitions • Determine the base case and general case of a recursive definition • Learn about recursive algorithms Java Programming: Guided Learning with Early Objects 2

Objectives (continued) • Learn about recursive methods • Become familiar with direct and indirect recursion • Learn how to use recursive methods to implement recursive algorithms Java Programming: Guided Learning with Early Objects 3

Recursive Definitions • Recursion: reducing a problem to successively smaller versions of itself – Powerful way to solve problems for which the solution is otherwise complicated Java Programming: Guided Learning with Early Objects 4

Recursive Definitions (continued) • Factorial: – 0! = 1 – n! = n ( n – 1)! if n > 0 equation 11 -1 equation 11 -2 • Equation 11 -1 is the base case • Equation 11 -2 is the general (recursive) case Java Programming: Guided Learning with Early Objects 5

Recursive Definitions (continued) • Recursion definition: defined in terms of a smaller version of itself • Every recursive definition must have at least one base case Java Programming: Guided Learning with Early Objects 6

Recursive Definitions (continued) • General case eventually must be reduced to a base case • Base case stops the recursion • Recursive algorithm: finds solution by reducing problems to smaller versions of itself Java Programming: Guided Learning with Early Objects 7

Recursive Definitions (continued) • Recursive method: method that calls itself – Body contains a statement that calls same method before completing the current call – Must have one or more base cases – General solution eventually must reduce to base case • Recursive algorithms implemented with recursive methods Java Programming: Guided Learning with Early Objects 8

Recursive Definitions (continued) • Factorial definition: public static int fact(int num) { if (num == 0) return 1; else return num * fact(num -1); } Java Programming: Guided Learning with Early Objects 9

Figure 11 -1 Execution of fact(4) Java Programming: Guided Learning with Early Objects 10

Recursive Definitions (continued) • Think of a recursive method as having unlimited copies of itself • Every recursive call has its own code, parameters, and local variables Java Programming: Guided Learning with Early Objects 11

Recursive Definitions (continued) • After completing a recursive call, control goes back to previous call • Current call must execute completely • Execution in previous call begins from point immediately following recursive call Java Programming: Guided Learning with Early Objects 12

Direct and Indirect Recursion • Directly recursive method calls itself • Indirectly recursive method calls another method – Eventually original method is called – Involves several methods – Can be elusive; take extra care in design Java Programming: Guided Learning with Early Objects 13

Infinite Recursion • If every recursive call results in another recursive call, method is infinitely recursive – Base case never executes • Every recursive call allocates memory – System saves information to transfer control back to caller Java Programming: Guided Learning with Early Objects 14

Infinite Recursion (continued) • Computer memory is finite • Infinitely recursive method continues until system runs out of memory Java Programming: Guided Learning with Early Objects 15

Designing Recursive Algorithms and Methods • Determine limiting conditions • Identify base cases – Provide direct solution to each base case • Identify general cases – Provide solution to each general case in terms of smaller version of itself Java Programming: Guided Learning with Early Objects 16

Problem Solving Using Recursion • Largest element in an array – list is name of array containing list elements – If list has length 1, single element is the largest – Find largest element by: max(list[a], largest(list[a+1]…list[b])) Java Programming: Guided Learning with Early Objects 17
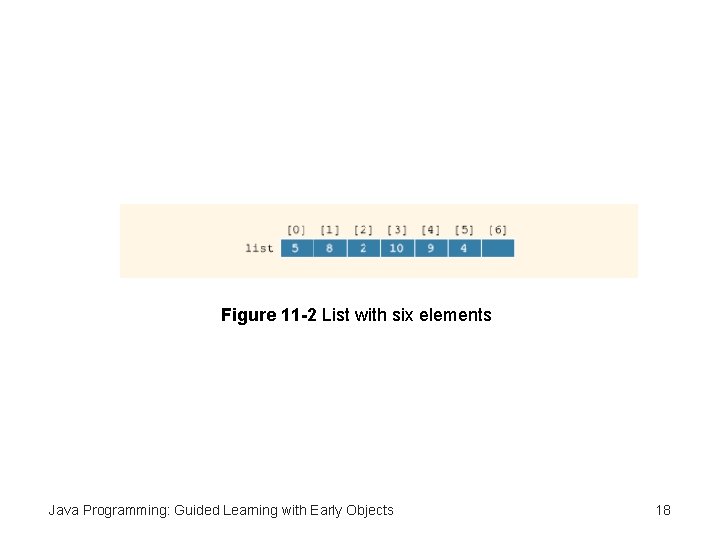
Figure 11 -2 List with six elements Java Programming: Guided Learning with Early Objects 18

Figure 11 -3 List with four elements Java Programming: Guided Learning with Early Objects 19
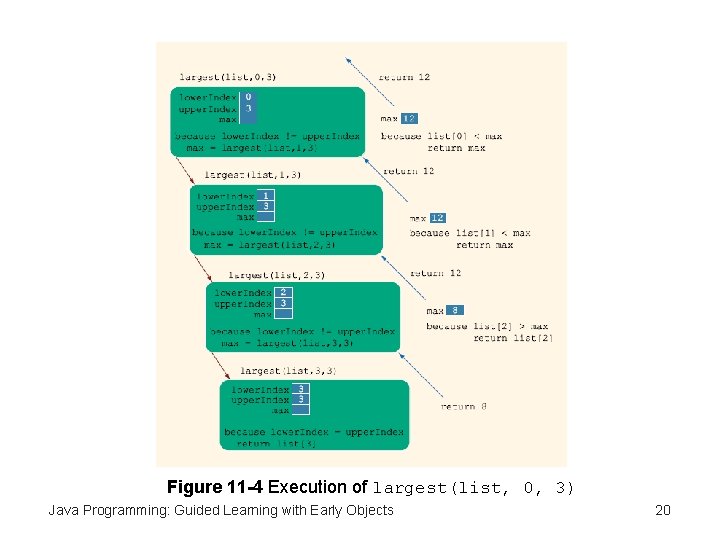
Figure 11 -4 Execution of largest(list, 0, 3) Java Programming: Guided Learning with Early Objects 20

Fibonacci Numbers • Recall Chapter 5 designed a program to determine a Fibonacci number – Each Fibonacci number is the sum of the previous two Java Programming: Guided Learning with Early Objects 21

Fibonacci Numbers (continued) Java Programming: Guided Learning with Early Objects 22

Fibonacci Numbers (continued) public static int Fib(int a, int b, int n){ if (n==1) return a; else if (n == 2) return b else return Fib(a, b, n-1) + Fib(a, b, n-2) } Java Programming: Guided Learning with Early Objects 23

Figure 11 -5 Execution of r. Fib. Num(2, 3, 5) Java Programming: Guided Learning with Early Objects 24

Towers of Hanoi • At creation of universe, priests in the temple of Brahma given three diamond needles • One needle contained 64 golden disks • Each disk slightly smaller than disks below it • Task: move all 64 disks from first needle to third Java Programming: Guided Learning with Early Objects 25

Towers of Hanoi (continued) • Rules: – Only one disk moved at a time – Removed disk must be placed on one of the other two needles – Larger disk cannot be placed on smaller disk • Once all disks moved from first needle to third, universe comes to an end Java Programming: Guided Learning with Early Objects 26
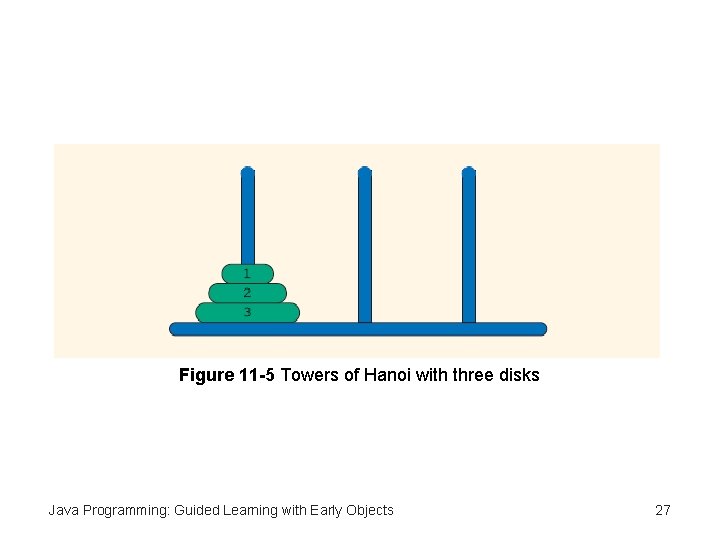
Figure 11 -5 Towers of Hanoi with three disks Java Programming: Guided Learning with Early Objects 27

Towers of Hanoi (continued) • One disk: – Base case – Move disk from needle one to needle three Java Programming: Guided Learning with Early Objects 28

Towers of Hanoi (continued) • Two disks: – First disk moves to second needle – Second disk moves to third needle – First disk moves to third needle Java Programming: Guided Learning with Early Objects 29

Towers of Hanoi (continued) • Three disks: – Two problems of moving two disks • 64 disks: – Two problems of moving 63 disks • n disks: – Two problems of moving n-1 disks Java Programming: Guided Learning with Early Objects 30
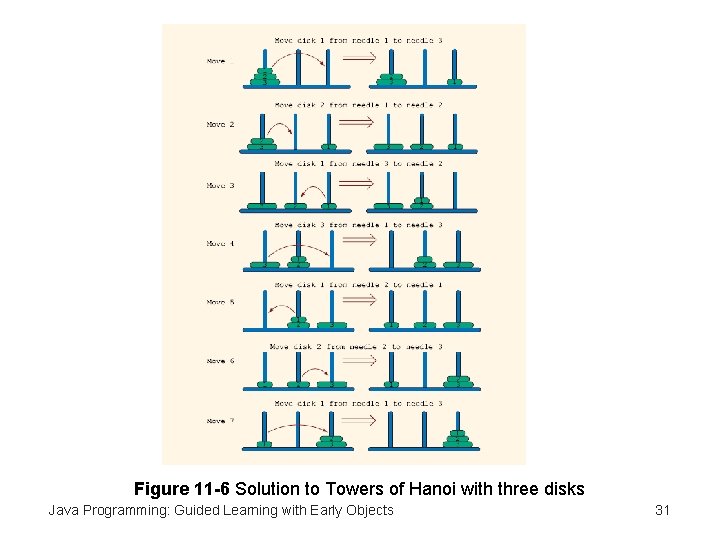
Figure 11 -6 Solution to Towers of Hanoi with three disks Java Programming: Guided Learning with Early Objects 31

Towers of Hanoi (continued) public static void move. Disks(int count, int needle 1, int needle 3, int needle 2) { if (count > 0) { move. Disks (count-1, needle 2, needle 3); move. Disks (count-1, needle 2, needle 3, needle 1); } } Java Programming: Guided Learning with Early Objects 32

Towers of Hanoi: Analysis • Needle 1 contains 64 disks – Number of moves to needle 3: 264 -1 ≈ 1. 6 x 1019 • Number of seconds in one year: 3. 2 x 107 Java Programming: Guided Learning with Early Objects 33

Towers of Hanoi: Analysis (continued) • Priests move one disk per second without resting: 5 x 1011 years • Estimated age of universe: 1. 5 x 1010 years • Computer: 1 billion moves per second, finishes in 500 years Java Programming: Guided Learning with Early Objects 34

Recursive Binary Search • • Recall binary search from Chapter 9 Find middle element Compare sought element with middle Repeat on half of list – Use method call Java Programming: Guided Learning with Early Objects 35
![Recursive Binary Search (continued) public static int r. Bin(int[] list, int first, int last, Recursive Binary Search (continued) public static int r. Bin(int[] list, int first, int last,](http://slidetodoc.com/presentation_image_h2/6ff439ebda25a9b1647ce578f3145d61/image-36.jpg)
Recursive Binary Search (continued) public static int r. Bin(int[] list, int first, int last, int srch. Itm ) { int mid; int location = 0; if (first <= last) { mid = (first + last)/2; if (list[mid] == srch. Itm) location = mid; Java Programming: Guided Learning with Early Objects 36
![Recursive Binary Search (continued) else if (list[mid] > srch. Itm) location = r. Bin(list, Recursive Binary Search (continued) else if (list[mid] > srch. Itm) location = r. Bin(list,](http://slidetodoc.com/presentation_image_h2/6ff439ebda25a9b1647ce578f3145d61/image-37.jpg)
Recursive Binary Search (continued) else if (list[mid] > srch. Itm) location = r. Bin(list, first, mid – 1, srch. Itm); else location = r. Bin(list, mid + 1, last, srch. Itm); }// end if first <= last if (first > location || last < location) location = -1; return location; }//end r. Bin Java Programming: Guided Learning with Early Objects 37
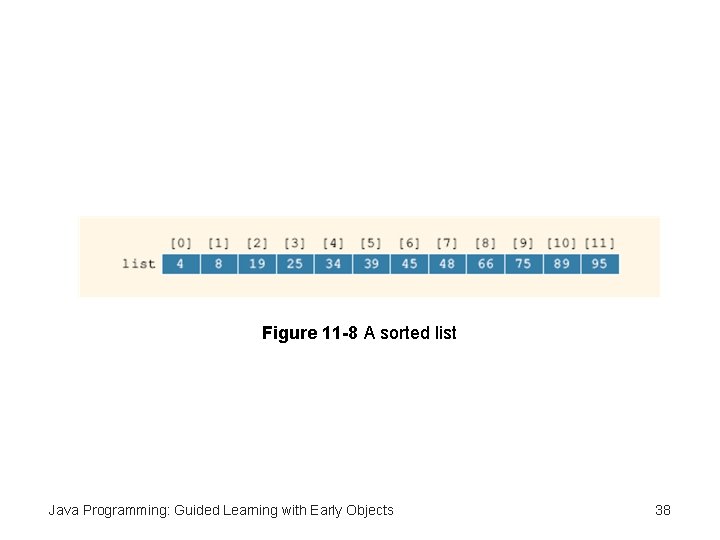
Figure 11 -8 A sorted list Java Programming: Guided Learning with Early Objects 38
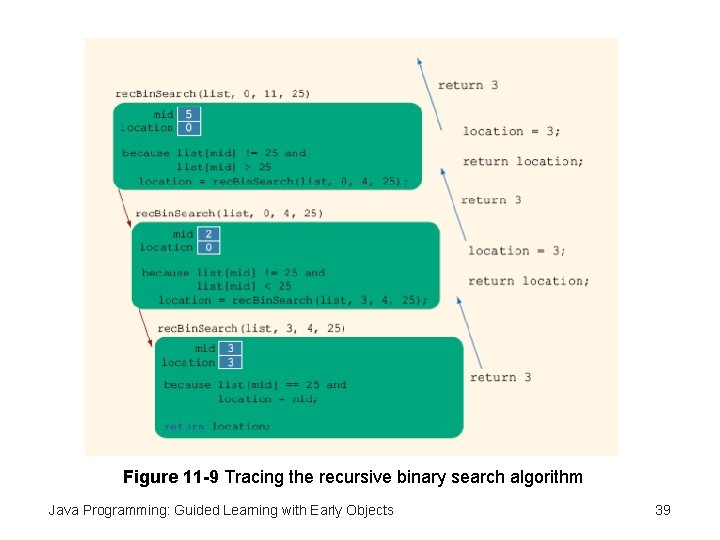
Figure 11 -9 Tracing the recursive binary search algorithm Java Programming: Guided Learning with Early Objects 39

Recursion or Iteration? • Often two ways to solve a problem: – Recursion – Iteration • Iterative algorithm often seems simpler • Iterative control structure: uses a looping structure to repeat a set of statements Java Programming: Guided Learning with Early Objects 40

Recursion or Iteration? (continued) • No general answer to which is better • Guidelines: – Nature of the solution – Efficiency of solution Java Programming: Guided Learning with Early Objects 41

Recursion or Iteration? (continued) • Every recursive call has its own parameters and local variables – Requires system to allocate space when method is called – Memory deallocated when method terminates • Recursive calls have overhead in memory and execution time Java Programming: Guided Learning with Early Objects 42

Recursion or Iteration? (continued) • Efficiency of programmer’s time also important consideration – Balance with execution efficiency • Choice may be a matter of personal preference • Any program that can be written recursively can be written iteratively • If iterative solution is at least as obvious and easy as recursive solution, choose iterative Java Programming: Guided Learning with Early Objects 43

Summary • Recursion: solving a problem by reducing it to smaller versions of itself • Recursive definition defines problem in terms of smaller versions of itself • Every recursive definition has one or more base cases • Recursive algorithm solves a problem by reducing it to smaller versions of itself Java Programming: Guided Learning with Early Objects 44

Summary (continued) • Solution to a problem in a base case obtained directly • Recursive method calls itself • Recursive algorithms implemented as recursive methods • Recursive method must have one or more base cases Java Programming: Guided Learning with Early Objects 45

Summary (continued) • General solution breaks problem into smaller versions of itself • General case eventually reduced to a base case • Base case stops the recursion Java Programming: Guided Learning with Early Objects 46

Summary (continued) • Tracing a recursive method: – Think of recursive method as having unlimited copies of itself – Every call to recursive method executes the code with its own set of parameters and variables Java Programming: Guided Learning with Early Objects 47

Summary (continued) • Tracing a recursive method (continued): – After completing recursive call, control goes back to calling environment – Current call executes completely before control returns – Execution in previous call continues from point following recursive call Java Programming: Guided Learning with Early Objects 48

Summary (continued) • Method is directly recursive if it calls itself • Method is indirectly recursive if it: – Calls another method – Eventually results in call to itself Java Programming: Guided Learning with Early Objects 49

Summary (continued) • Design a recursive method: – Understand problem requirements – Determine limiting conditions – Identify base cases • Provide direct solution to base cases – Identify general cases • Provide recursive solution to each general case Java Programming: Guided Learning with Early Objects 50
- Slides: 50