Java Object Oriented Programming Recursion Objectives Learn how

Java Object Oriented Programming Recursion

Objectives: • Learn how to use recursion to solve problems that are defined in terms of smaller problems. Lab 11 -2

Recursion • A recursive solution describes a procedure for a particular task in terms of applying the same procedure to a similar but smaller task. • A recursive solution must have a base case when the task is so simple that no recursion is needed. • Recursive calls must eventually converge to a base case. Lab 11 -3
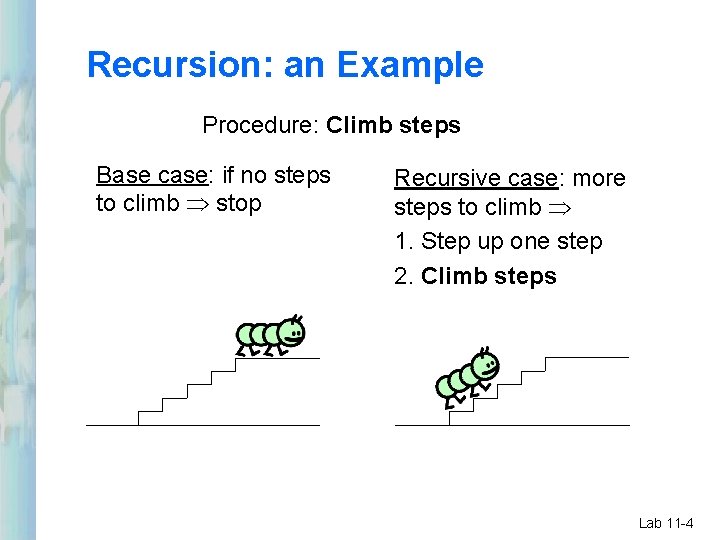
Recursion: an Example Procedure: Climb steps Base case: if no steps to climb stop Recursive case: more steps to climb 1. Step up one step 2. Climb steps Lab 11 -4
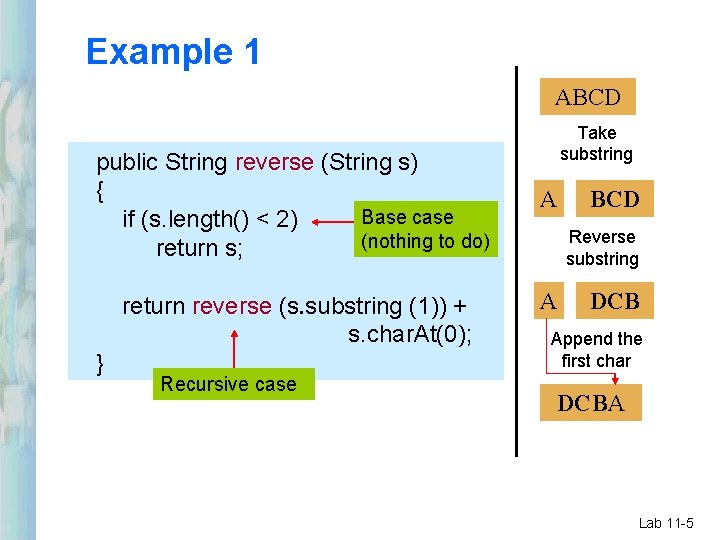
Example 1 ABCD public String reverse (String s) { Base case if (s. length() < 2) (nothing to do) return s; return reverse (s. substring (1)) + s. char. At(0); } Recursive case Take substring A BCD Reverse substring A DCB Append the first char DCBA Lab 11 -5
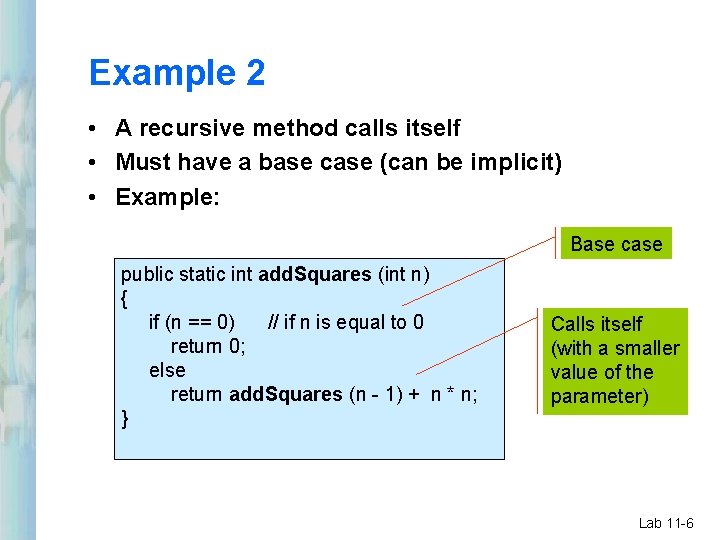
Example 2 • A recursive method calls itself • Must have a base case (can be implicit) • Example: Base case public static int add. Squares (int n) { if (n == 0) // if n is equal to 0 return 0; else return add. Squares (n - 1) + n * n; } Calls itself (with a smaller value of the parameter) Lab 11 -6
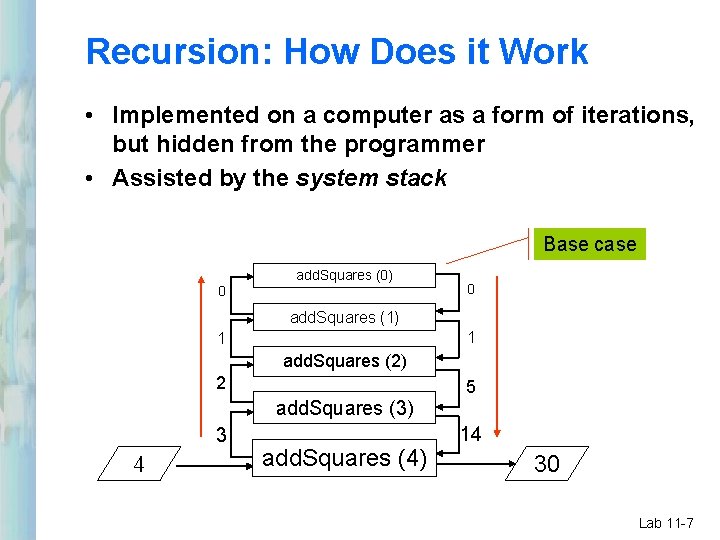
Recursion: How Does it Work • Implemented on a computer as a form of iterations, but hidden from the programmer • Assisted by the system stack Base case 0 add. Squares (0) 0 add. Squares (1) 1 1 add. Squares (2) 2 add. Squares (3) 3 4 add. Squares (4) 5 14 30 Lab 11 -7

Top-Down Programming Lab 11 -8

Top-Down Programming (cont’d) • Write a program that reads a series of numbers from the keyboard and identifies which are prime numbers and which are not. • We will use a recursive method is. Prime that receives an integer argument and returns true if the argument is a prime number, false otherwise. Lab 11 -9

Top-Down Programming (cont’d) • A prime number (or a prime) is a natural number that has exactly two distinct natural number divisors: 1 and itself. • A solution can be found by recursively dividing the number by every areanumber from 2 to ½ the original number. • For every number starting with 2, if the divisor is greater than the number / 2 then the number is a prime number. (A base case) • If the number is evenly divisible by the divisor then the number is not a prime number. • If neither of these conditions is true call is prime with the next largest divisor. Lab 11 -10

Top-Down Programming (cont’d) • Start JCreator. • Open the file called “Prime. Numbers. java”. • “Prime. Numbers. java” is in your Lab 11 folder. Lab 11 -11

Top-Down Programming (cont’d) import java. util. Scanner; public class Prime. Numbers { private int number; public static void main(String[ ] args) { for (int i = 0; i < 5; i++) { Prime. Numbers lab = new Prime. Numbers( ); lab. input(); // Read data from the keyboard lab. output( ); // Display output } } } Lab 11 -12

Top-Down Programming (cont’d) input Lab 11 -13

Top-Down Programming (cont’d) private void input() { Scanner kybd = new Scanner(System. in); System. out. print("Enter an integer: "); number = kybd. next. Int(); } Lab 11 -14

Top-Down Programming (cont’d) output Lab 11 -15

Top-Down Programming (cont’d) private void output() { if ( is. Prime(number, 2) ) System. out. println(number + " is a prime number!"); else System. out. println(number + " is not a prime number!"); System. out. println(); } Lab 11 -16

Top-Down Programming (cont’d) is. Prime Lab 11 -17

Top-Down Programming (cont’d) private static boolean is. Prime(int n, int q) { } Lab 11 -18

Top-Down Programming (cont’d) private static boolean is. Prime(int n, int q) { if (q > n / 2) return true; } Lab 11 -19

Top-Down Programming (cont’d) private static boolean is. Prime(int n, int q) { if (q > n / 2) return true; else if (n % q == 0) return false; } Lab 11 -20

Top-Down Programming (cont’d) private static boolean is. Prime(int n, int q) { if (q > n / 2) return true; else if (n % q == 0) return false; return is. Prime(n, q + 1); } Lab 11 -21

Top-Down Programming (cont’d) Run The Program: Enter five integers: 31 82 45 73 121 31 is a prime number! 82 is not a prime number! 45 is not a prime number! 73 is a prime number! 121 is not a prime number! Lab 11 -22

Java Object Oriented Programming Solving The Line Segment Problem 16 cm

Start with a segment 16 cm in length. At each end draw a segment half as long, perpendicular to the original segment and intersecting at the new segment’s midpoing. If this process is continued infinitely, a fractal is created. Counting the original segment as stage 1, find the length of each segment at any given stage. Lab 11 -24

Top-Down Programming (cont’d) • Start JCreator. • Open the file called “Line. Segment. java”. • “Line. Segment. java” is in your Lab 11 folder. Lab 11 -25

A Recursive Solution To Determine The Length Of A Segment given the stage as an argument. public double segment(int n) { } Lab 11 -26

Where the stage is represented by the variable n: When n = 1, how long is the segment? 16 cm Lab 11 -27

Where the stage is represented by the variable n: When n = 1, how long is the segment? 16 cm What is the base case? Lab 11 -28
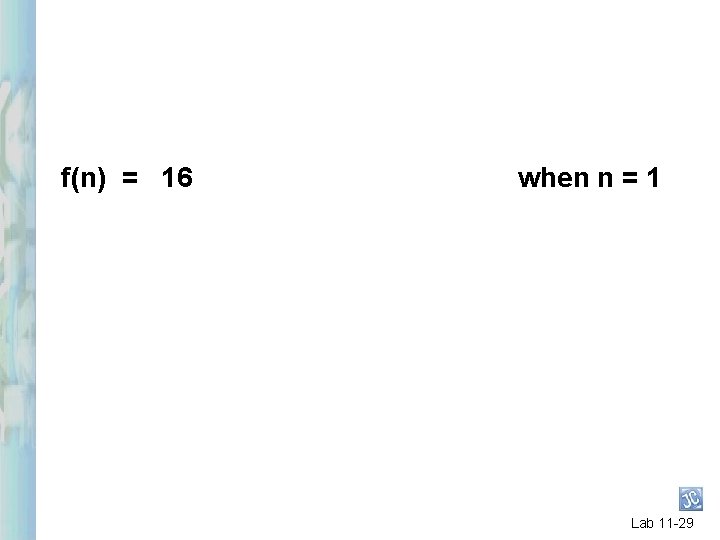
f(n) = 16 when n = 1 Lab 11 -29

A Recursive Solution To Determine The Length Of A Segment given the stage as an argument. public static double segment(int n) { if (n == 1) return 16; } Lab 11 -30
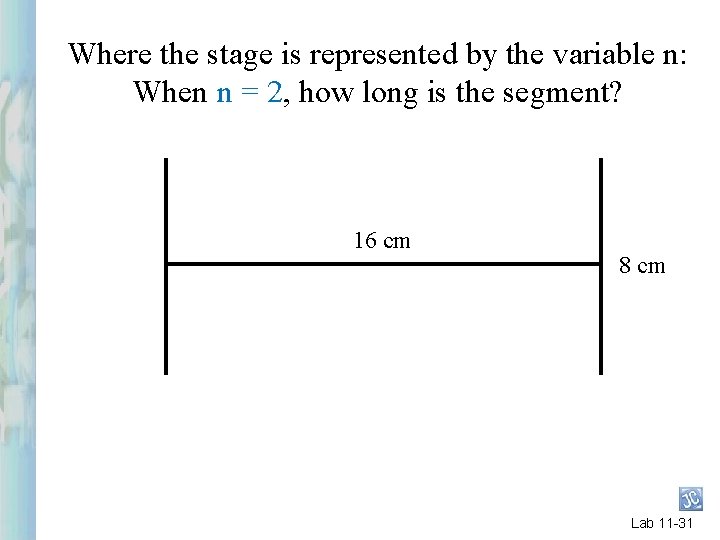
Where the stage is represented by the variable n: When n = 2, how long is the segment? 16 cm 8 cm Lab 11 -31
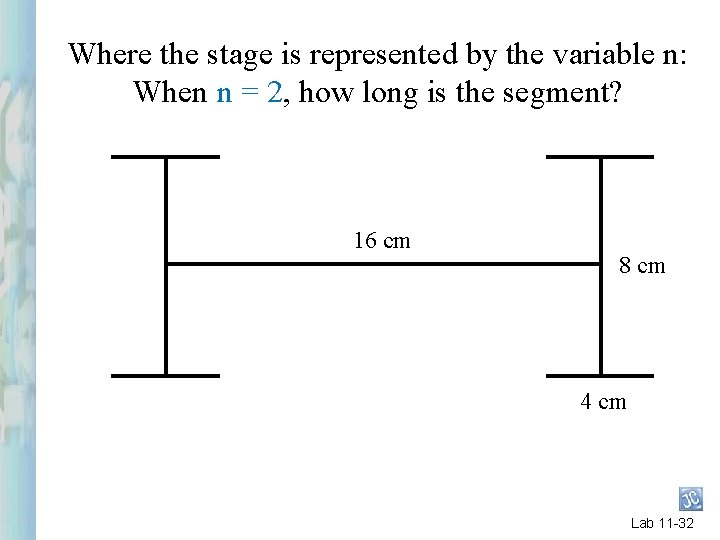
Where the stage is represented by the variable n: When n = 2, how long is the segment? 16 cm 8 cm 4 cm Lab 11 -32
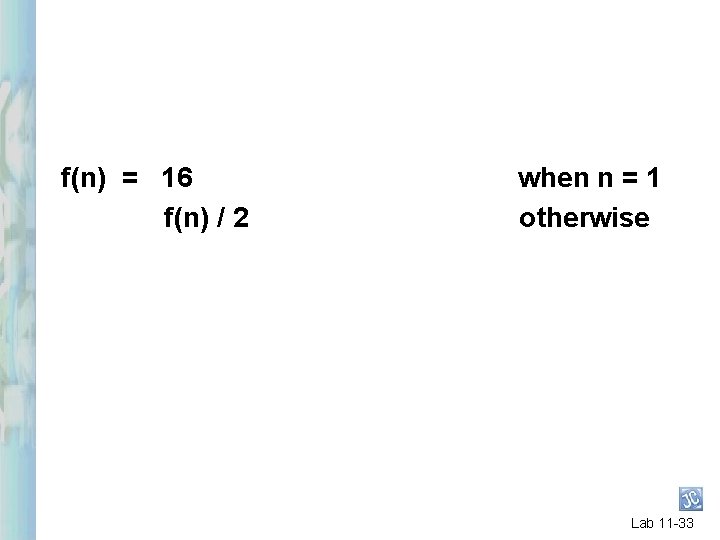
f(n) = 16 f(n) / 2 when n = 1 otherwise Lab 11 -33

A Recursive Solution To Determine The Length Of A Segment given the stage as an argument. public static double segment(int n) { if (n == 1) return 16; // Each segment is half as long as the // peceeding segment. return segment(n – 1) / 2. 0; } Lab 11 -34

Java Object Oriented Programming Solving The Triangle Problem

Consider the following recursive algorithm: Given an equilateral triangle, connect the midpoints of the sides. Paint the triangle formed. Repeat the process 4 more times with all the remaining unpainted triangles. How many triangles will be painted? Lab 11 -36

Top-Down Programming (cont’d) • Start JCreator. • Open the file called “Triangles. java”. • “Triangles. java” is in your Lab 11 folder. Lab 11 -37
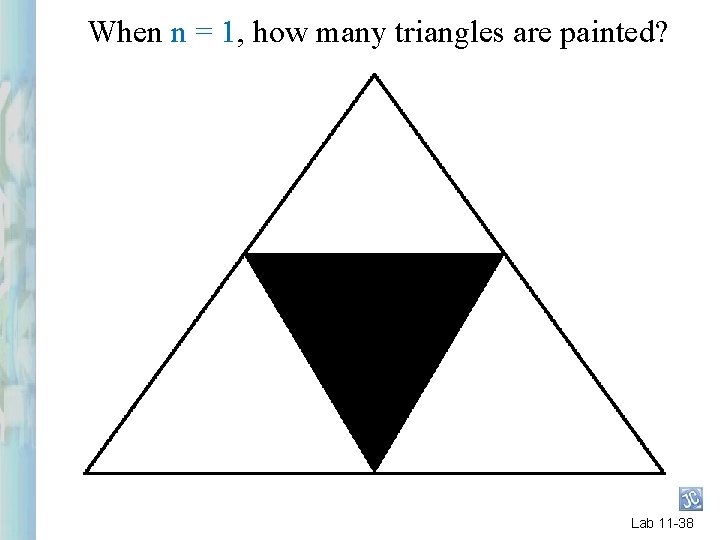
When n = 1, how many triangles are painted? Lab 11 -38

1 Lab 11 -39

What is the base case? Lab 11 -40
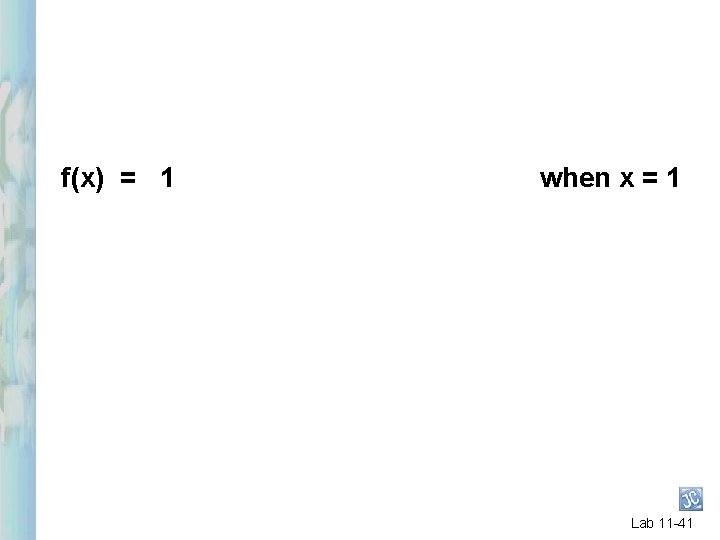
f(x) = 1 when x = 1 Lab 11 -41

public static int triangles(int n) { if (n == 1) return 1; } Lab 11 -42
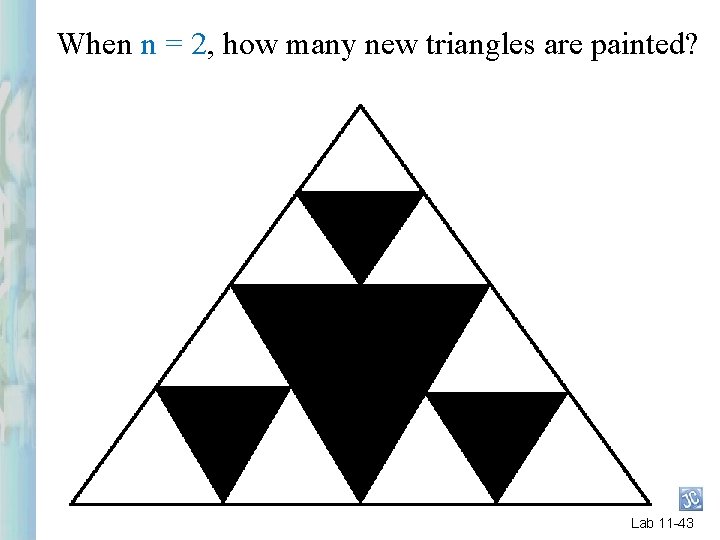
When n = 2, how many new triangles are painted? Lab 11 -43

3 Lab 11 -44
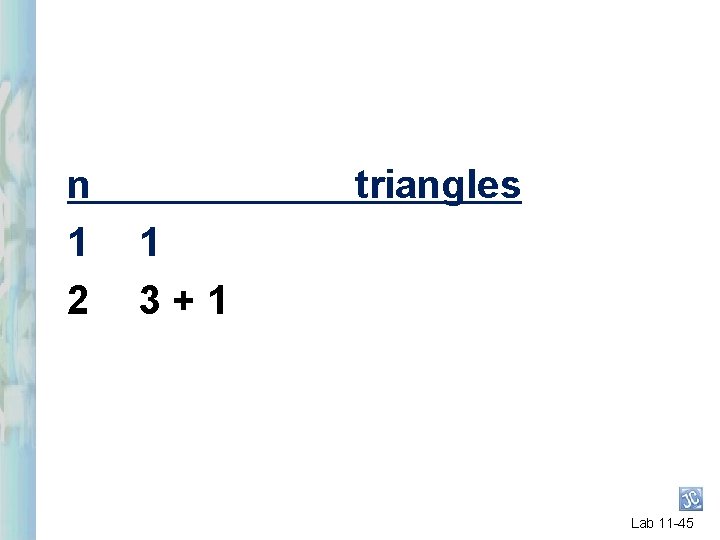
n 1 2 triangles 1 3+1 Lab 11 -45
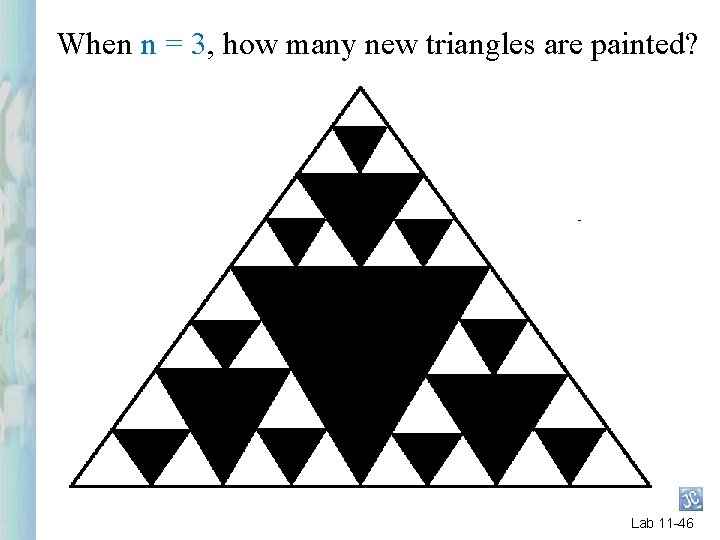
When n = 3, how many new triangles are painted? Lab 11 -46

9 Lab 11 -47
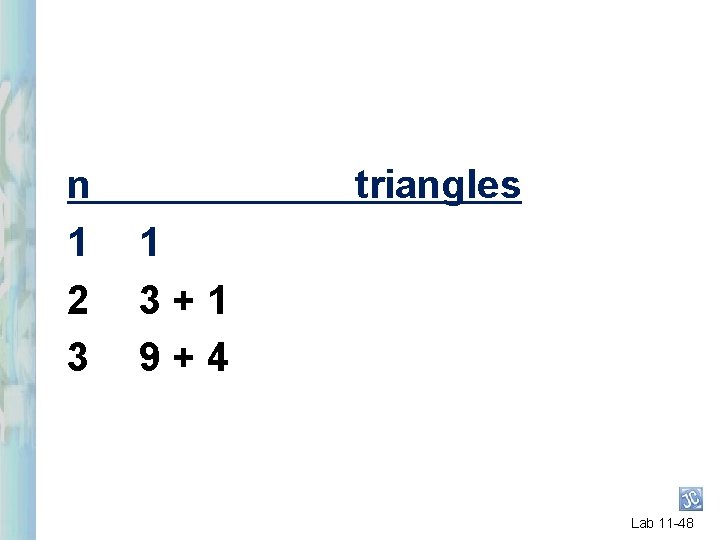
n 1 2 3 triangles 1 3+1 9+4 Lab 11 -48
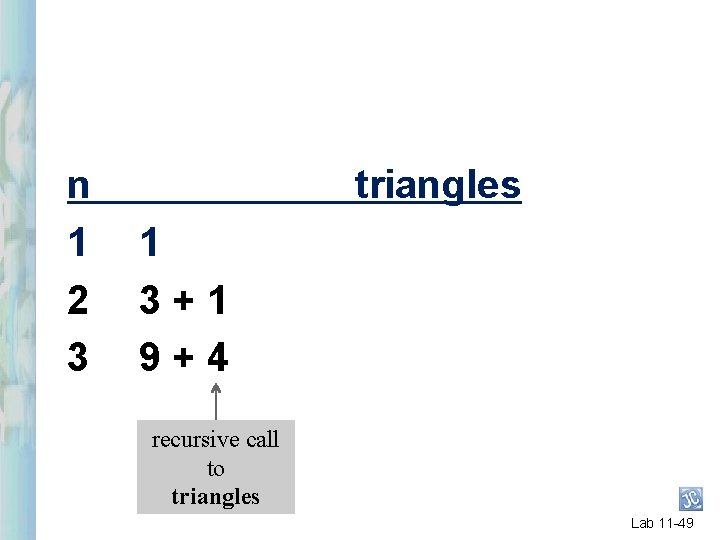
n 1 2 3 triangles 1 3+1 9+4 recursive call to triangles Lab 11 -49
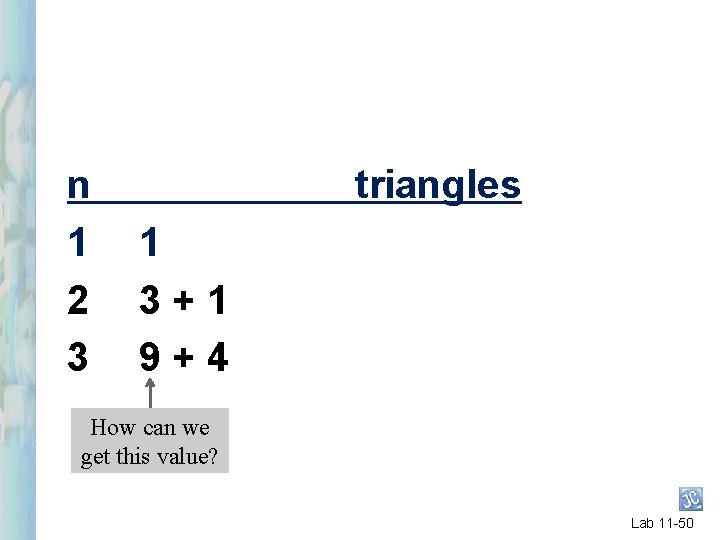
n 1 2 3 triangles 1 3+1 9+4 How can we get this value? Lab 11 -50

Math. pow(3, n – 1) Lab 11 -51
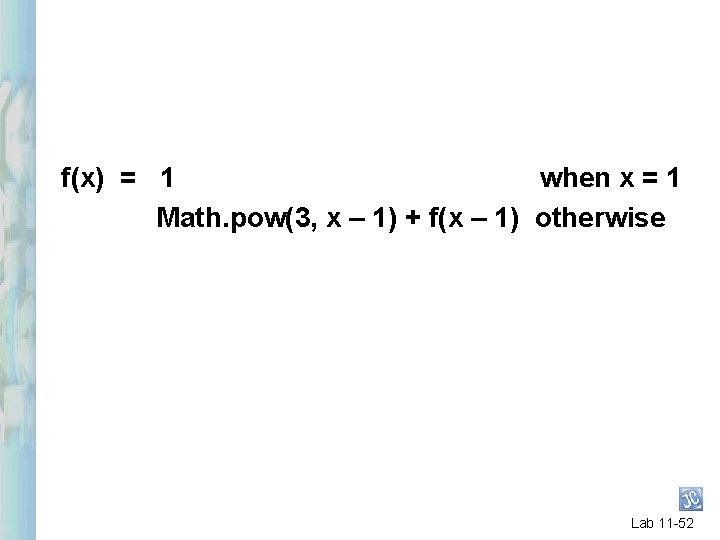
f(x) = 1 when x = 1 Math. pow(3, x – 1) + f(x – 1) otherwise Lab 11 -52

public static int triangles(int n) { if (n == 1) return 1; return (int) Math. pow(3, n – 1) + triangles(n – 1); } Lab 11 -53

Questions? Lab 11 -54

Java Object Oriented Programming Begin Lab 11
- Slides: 55