Jamming Andrea J Liu Department of Physics Astronomy

Jamming Andrea J. Liu Department of Physics & Astronomy University of Pennsylvania Corey S. O’Hern Leo E. Silbert Jen M. Schwarz Lincoln Chayes Sidney R. Nagel Mechanical Engineering, Yale Univ. Physics, Southern Ill. Univ. Physics, Syracuse Univ. Mathematics, UCLA James Franck Inst. , U Chicago Brought to you by NSF-DMR-0087349, DOE DE-FG 02 -03 ER 46087

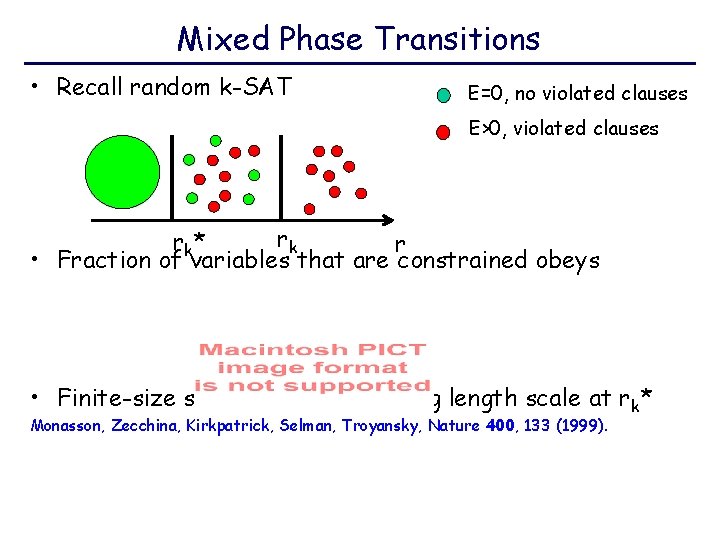
Mixed Phase Transitions • Recall random k-SAT E=0, no violated clauses E>0, violated clauses rk r k* r • Fraction of variables that are constrained obeys • Finite-size scaling shows diverging length scale at rk* Monasson, Zecchina, Kirkpatrick, Selman, Troyansky, Nature 400, 133 (1999).

Mixed Phase Transitions • “infinite-dimensional” models – p-spin interaction spin glass Kirkpatrick, Thirumalai, PRL 58, 2091 (1987). – k-core (bootstrap) Chalupa, Leath, Reich, J. Phys. C (1979); Pittel, Spencer, Wormald, J. Comb. Th. Ser. B 67, 111 (1996). – Random k-SAT Monasson, Zecchina, Kirkpatrick, Selman, Troyansky, Nature 400, 133 (1999). - etc. • But physicists really only care about finite dimensions – Jamming transition of spheres O’Hern, Langer, Liu, Nagel, PRL 88, 075507 (2002). – Knights models Toninelli, Biroli, Fisher, PRL 96, 035702 (2006). – k-core + “force-balance” models Schwarz, Liu, Chayes, Europhys. Lett. 73, 560 (2006).

Stress Relaxation Time • Behavior of glassforming liquids depends on how long you wait – At short time scales, silly putty behaves like a solid – At long time scales, silly putty behaves like a liquid Stress relaxation time t: how long you need to wait for system to behave like liquid

Glass Transition When liquid cools, stress relaxation time increases • When liquid crystallizes – Particles order – Stress relaxation time suddenly jumps • When liquid is cooled through glass transition – Particles remain disordered – Stress relaxation time increases continuously “Picture Book of Sir John Mandeville’s Travels, ” ca. 1410.

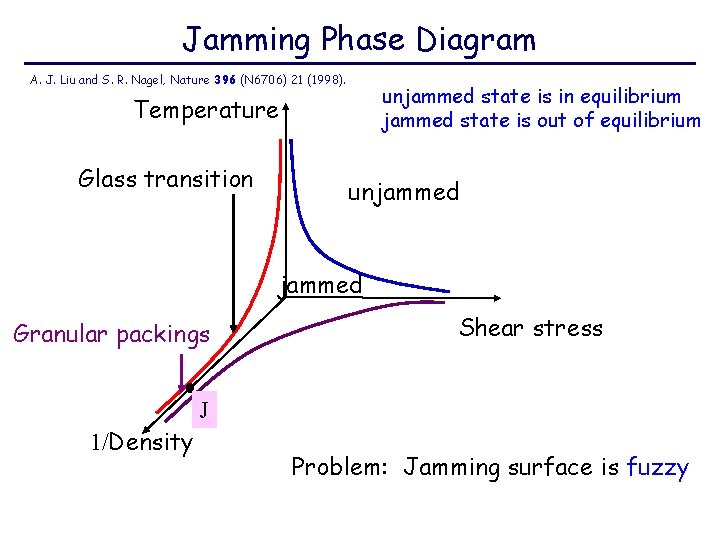
Jamming Phase Diagram A. J. Liu and S. R. Nagel, Nature 396 (N 6706) 21 (1998). unjammed state is in equilibrium jammed state is out of equilibrium Temperature Glass transition unjammed Granular packings Shear stress J 1/Density Problem: Jamming surface is fuzzy

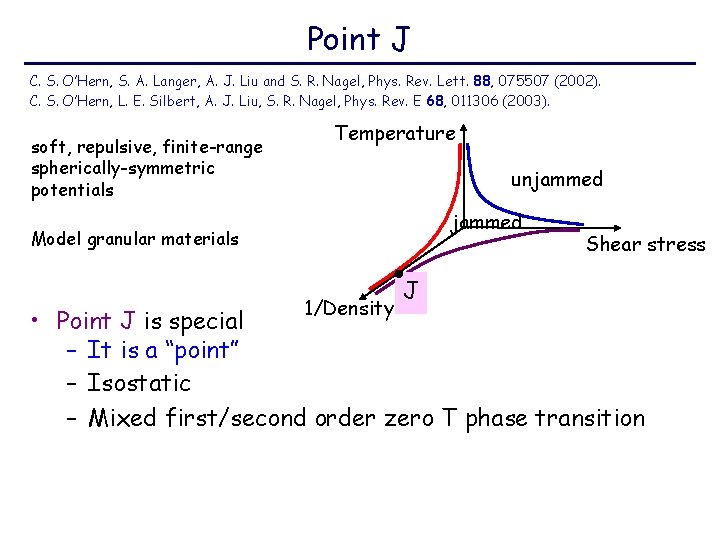
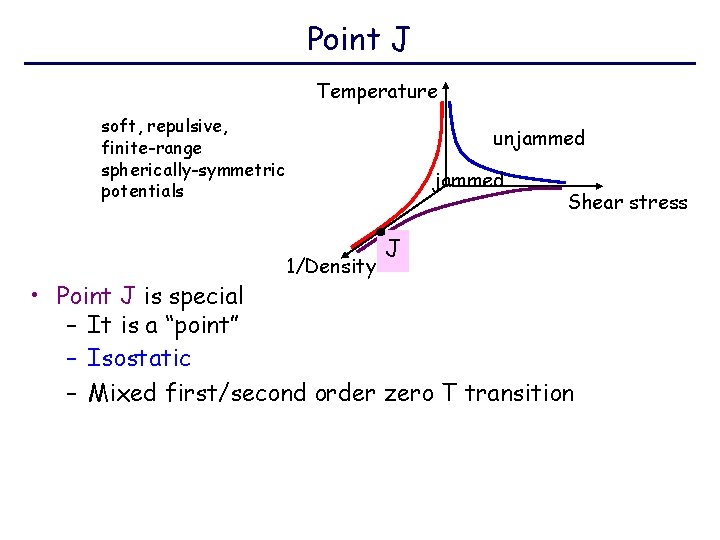
Point J C. S. O’Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Phys. Rev. Lett. 88, 075507 (2002). C. S. O’Hern, L. E. Silbert, A. J. Liu, S. R. Nagel, Phys. Rev. E 68, 011306 (2003). soft, repulsive, finite-range spherically-symmetric potentials Temperature unjammed Model granular materials 1/Density J Shear stress • Point J is special – It is a “point” – Isostatic – Mixed first/second order zero T phase transition

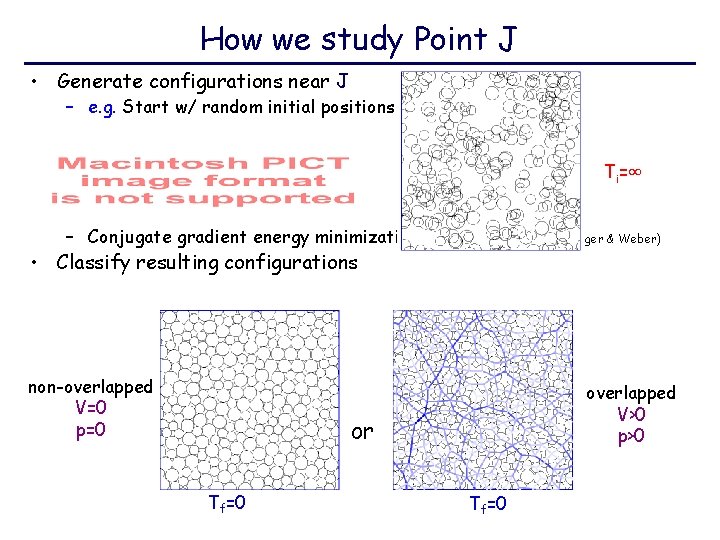
How we study Point J • Generate configurations near J – e. g. Start w/ random initial positions Ti=∞ – Conjugate gradient energy minimization (Inherent structures, Stillinger & Weber) • Classify resulting configurations non-overlapped V=0 p=0 overlapped V>0 p>0 or Tf=0

- Onset of Jamming is Onset of Overlap D=2 D=3 - • Pressures for different states collapse on a single curve - • Shear modulus and pressure vanish at the same c -4 -3 -2 c) rather than individual configs (c. f. Torquato) • We focus log( on ensemble • Good ensemble is fixed - c, or fixed pressure

How Much Does c Vary Among States? • Distribution of c values narrows as system size grows 0 w • Distribution approaches delta-function as N • Essentially all configurations jam at one packing density Of course, there is a tail up to close-packed crystal • J is a “POINT”

0 log( *- 0) Point J is at Random Close-Packing w • Where do virtually all states jam in infinite system limit? 2 d (bidisperse) 3 d (monodisperse) These are values associated with random close-packing!

Point J Temperature soft, repulsive, finite-range spherically-symmetric potentials unjammed 1/Density Shear stress J • Point J is special – It is a “point” – Isostatic – Mixed first/second order zero T transition

Number of Overlaps/Particle Z Just below c, no particles overlap Just above c there are Zc overlapping neighbors per particle (2 D) (3 D) - - - log( - c) -

Isostaticity • What is the minimum number of interparticle contacts needed for mechanical equilibrium? • No friction, spherical particles, D dimensions – Match unknowns (number of interparticle normal forces) to equations (force balance for mechanical stability) – Number of unknowns per particle=Z/2 – Number of equations per particle = D • Point J is purely geometrical!

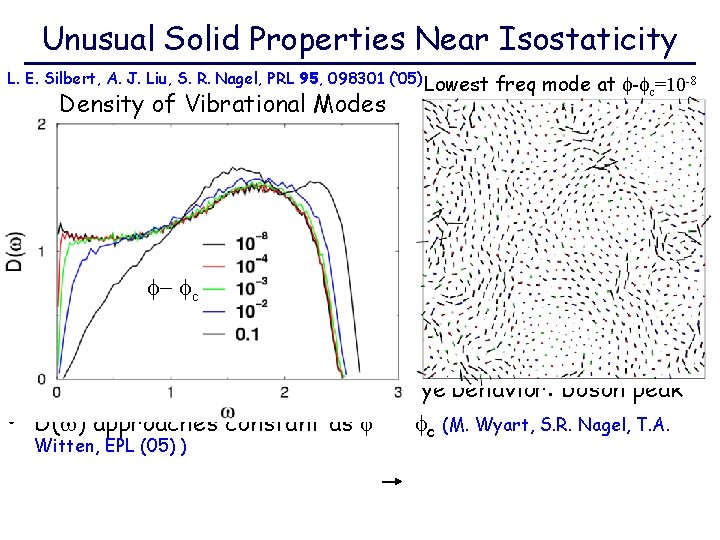
Unusual Solid Properties Near Isostaticity L. E. Silbert, A. J. Liu, S. R. Nagel, PRL 95, 098301 (‘ 05) Lowest Density of Vibrational Modes freq mode at - c=10 -8 - c • Excess low-w modes swamp w 2 Debye behavior: boson peak • D(w) approaches constant as c (M. Wyart, S. R. Nagel, T. A. Witten, EPL (05) )

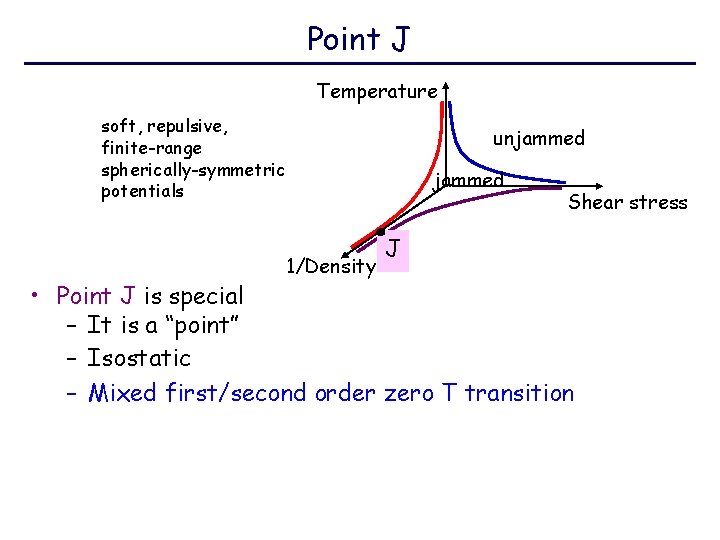
Point J Temperature soft, repulsive, finite-range spherically-symmetric potentials unjammed 1/Density Shear stress J • Point J is special – It is a “point” – Isostatic – Mixed first/second order zero T transition

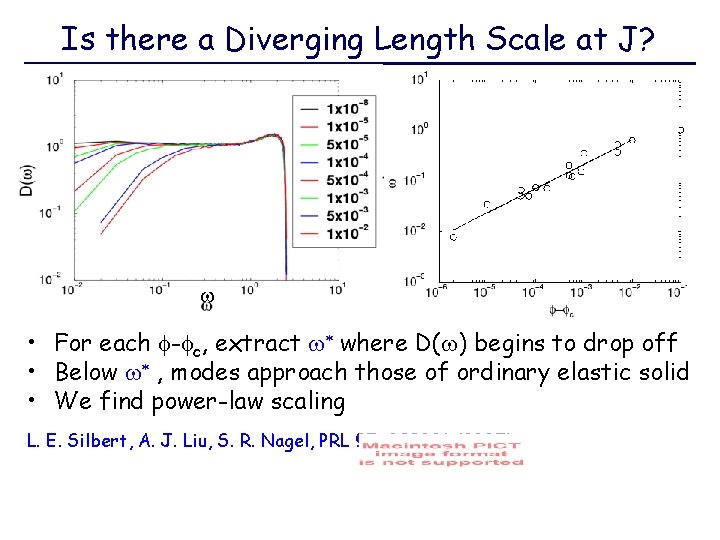
Is there a Diverging Length Scale at J? w • For each - c, extract w* where D(w) begins to drop off • Below w* , modes approach those of ordinary elastic solid • We find power-law scaling L. E. Silbert, A. J. Liu, S. R. Nagel, PRL 95, 098301 (2005)

Frequency Scale implies Length Scale • The frequency w* has a corresponding eigenmode • • Decompose eigenmode in plane waves Dominant wavevector contribution is at peak of f. T(k, w*) extract k*: We also expect with

Summary of Jamming Transition • Mixed first-order/second-order transition • Number of overlapping neighbors per particle • Static shear modulus • Diverging length scale • And perhaps also

Jamming vs K-Core (Bootstrap) Percolation • Jammed configs at T=0 are mechanically stable • For particle to be locally stable, it must have at least d+1 overlapping neighbors in d dimensions • Each of its overlapping nbrs must have at least d+1 overlapping nbrs, etc. • At > c all particles in load-bearing network have at least d+1 neighbors • Consider lattice with coord. # Zmax with sites indpendently occupied with probability p • For site to be part of “kcore”, it must be occupied and have at least k=d+1 occupied neighbors • Each of its occ. nbrs must have at least k occ. nbrs, etc. • Look for percolation of the k-core

K-core Percolation on the Bethe Lattice • K-core percolation is exactly solvable on Bethe lattice • This is mean-field solution • Let K=probability of infinite kconnected cluster • For k>2 we find • Recall simulation results Chalupa, Leath, Reich, J. Phys. C (1979) Pittel, et al. , J. Comb. Th. Ser. B 67, 111 (1996) J. M. Schwarz, A. J. Liu, L. Chayes, EPL (06)

K-Core Percolation in Finite Dimensions • There appear to be at least 3 different types of k-core percolation transitions in finite dimensions 1. Continuous percolation (Charybdis) 2. No percolation until p=1 (Scylla) 3. Discontinuous percolation? 1. Yes, for k-core variants Knights models (Toninelli, Biroli, Fisher) k-core with pseudo force-balance (Schwarz, Liu, Chayes)

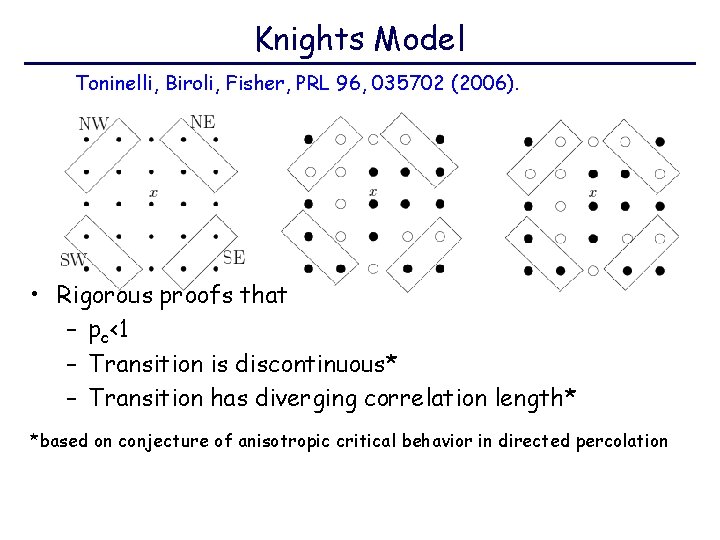
Knights Model Toninelli, Biroli, Fisher, PRL 96, 035702 (2006). • Rigorous proofs that – pc<1 – Transition is discontinuous* – Transition has diverging correlation length* *based on conjecture of anisotropic critical behavior in directed percolation

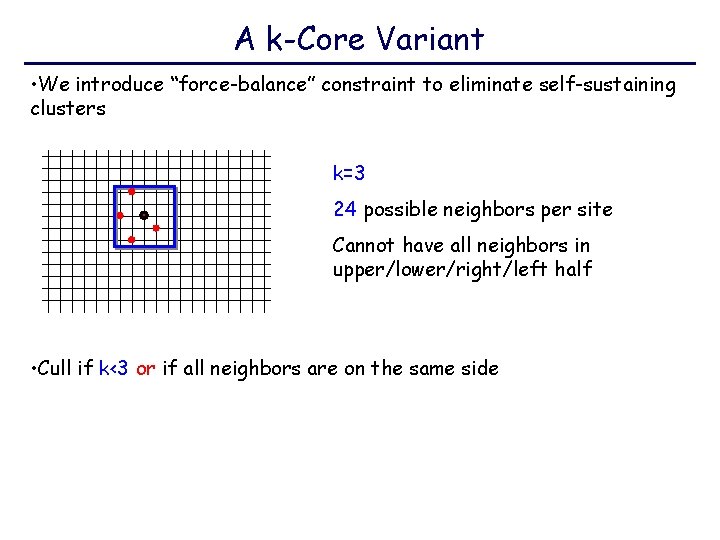
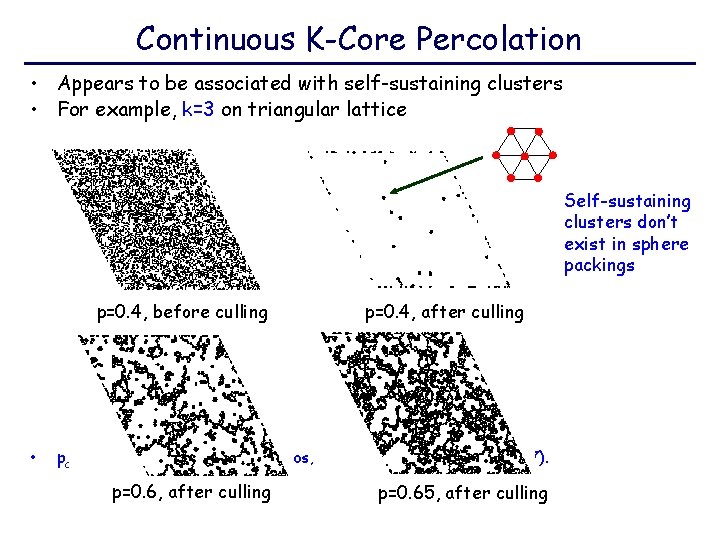
A k-Core Variant • We introduce “force-balance” constraint to eliminate self-sustaining clusters k=3 24 possible neighbors per site Cannot have all neighbors in upper/lower/right/left half • Cull if k<3 or if all neighbors are on the same side

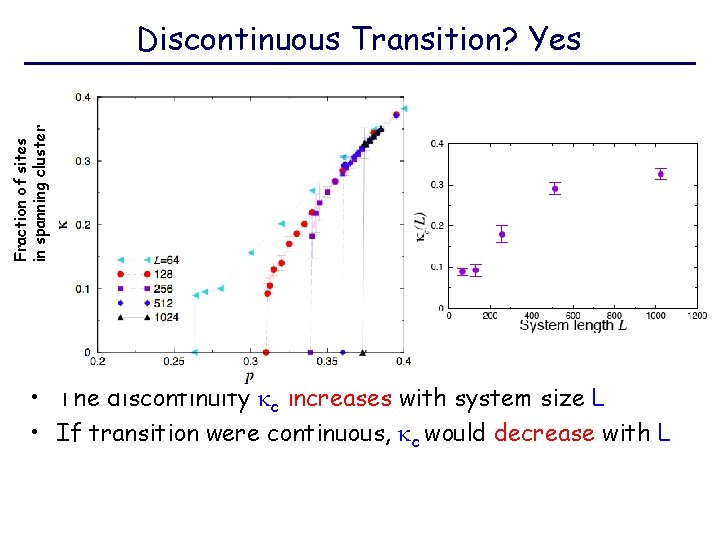
Fraction of sites in spanning cluster Discontinuous Transition? Yes • The discontinuity c increases with system size L • If transition were continuous, c would decrease with L

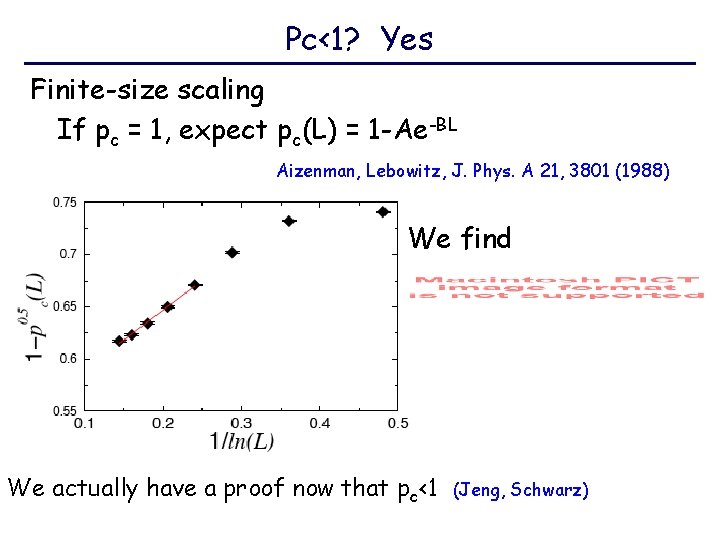
Pc<1? Yes Finite-size scaling If pc = 1, expect pc(L) = 1 -Ae-BL Aizenman, Lebowitz, J. Phys. A 21, 3801 (1988) We find We actually have a proof now that pc<1 (Jeng, Schwarz)

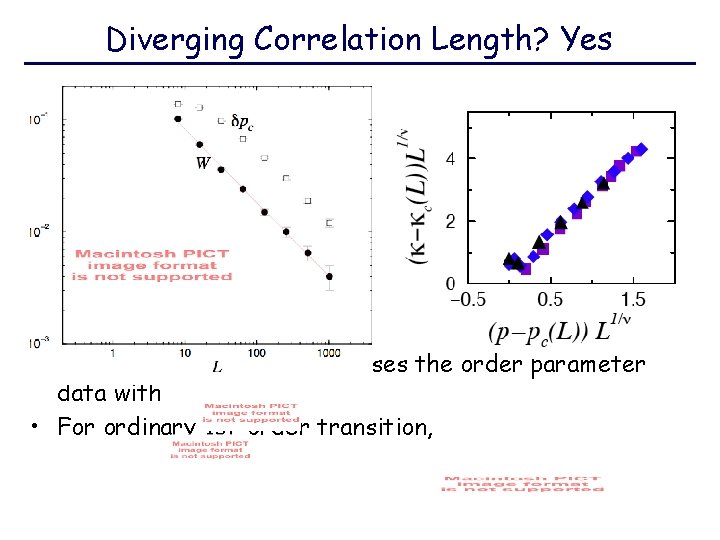
Diverging Correlation Length? Yes • This value of collapses the order parameter data with • For ordinary 1 st-order transition,

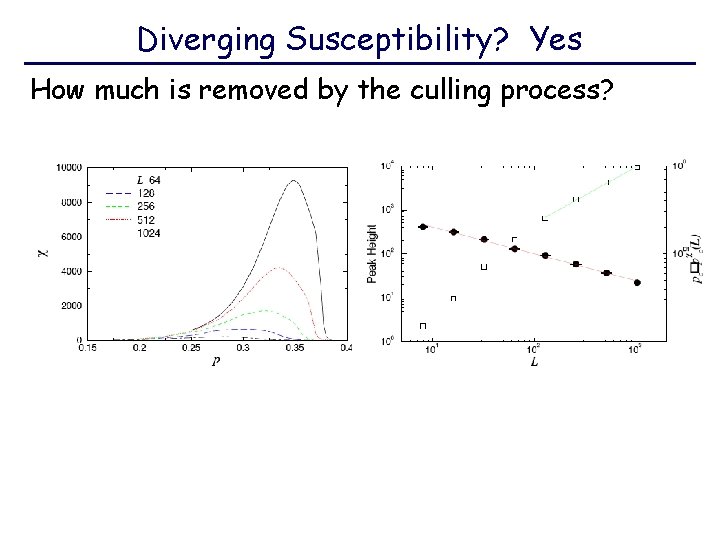
Diverging Susceptibility? Yes How much is removed by the culling process?

BUT • Exponents for k-core variants in d=2 are different from those in mean-field! Mean field d=2 Why does Point J show mean-field behavior? • Point J may have critical dimension of dc=2 due to isostaticity (Wyart, Nagel, Witten) • Isostaticity is a global condition not captured by local kcore requirement of k neighbors Henkes, Chakraborty, PRL 95, 198002 (2005).

Similarity to Other Models • The discontinuity & exponents we observe are rare but have been found in a few models – Mean-field p-spin interaction spin glass (Kirkpatrick, Thirumalai, Wolynes) – Mean-field dimer model (Chakraborty, et al. ) – Mean-field kinetically-constrained models (Fredrickson, Andersen) – Mode-coupling approximation of glasses (Biroli, Bouchaud) • These models all exhibit glassy dynamics!! First hint of UNIVERSALITY in jamming

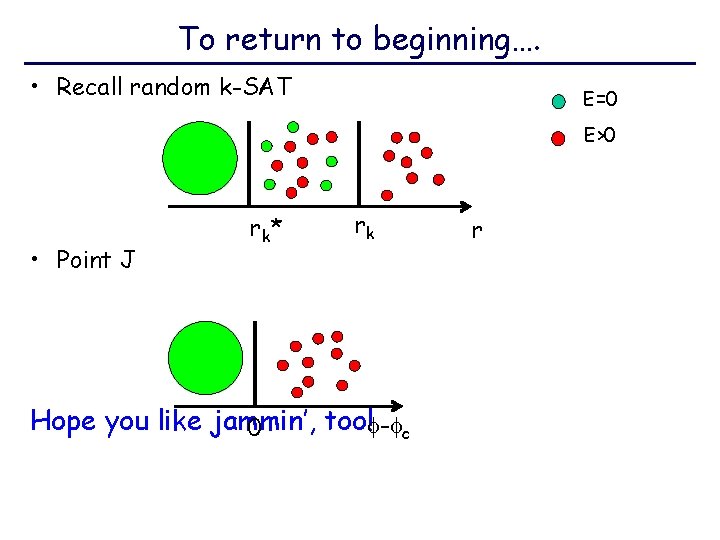
To return to beginning…. • Recall random k-SAT E=0 E>0 • Point J r k* rk Hope you like jammin’, too! - c 0 r

Conclusions • Point J is a special point T • Common exponents in different jamming models in mean field! • But different in finite dimensions 1/r sxy J Hope you like jammin’, too! • Thanks to NSF-DMR-0087349 DOE DE-FG 02 -03 ER 46087

Continuous K-Core Percolation • Appears to be associated with self-sustaining clusters • For example, k=3 on triangular lattice Self-sustaining clusters don’t exist in sphere packings p=0. 4, before culling • p=0. 4, after culling pc=0. 6921± 0. 0005, M. C. Madeiros, C. M. Chaves, Physica A (1997). p=0. 6, after culling p=0. 65, after culling

No Transition Until p=1 • E. g. k=3 on square lattice There is a positive probability that there is a large empty square whose boundary is not completely occupied Voids unstable to shrinkage, not growth in sphere packings After culling process, the whole lattice will be empty Straley, van Enter J. Stat. Phys. 48, 943 (1987). M. Aizenmann, J. L. Lebowitz, J. Phys. A 21, 3801 (1988). R. H. Schonmann, Ann. Prob. 20, 174 (1992). C. Toninelli, G. Biroli, D. S. Fisher, Phys. Rev. Lett. 92, 185504 (2004).

Point J and the Glass Transition • Point J only exists for repulsive, finite-range potentials • Real liquids have attractions U Repulsion vanishes at finite distance r • Attractions serve to hold system at high enough density that repulsions come into play (WCA)