Its All About Acceleration Using Velocity Vectors on

It’s All About Acceleration

Using Velocity Vectors on Motion Diagrams (Quick Review) © 2015 Pearson Education, Inc.

Using Vectors on Motion Diagrams • In two dimensions, an object’s displacement is a vector: • The velocity vector is simply the displacement vector multiplied by the scalar 1/Δt. • Consequently the velocity vector points in the direction of the displacement. © 2015 Pearson Education, Inc. Slide 3 -3

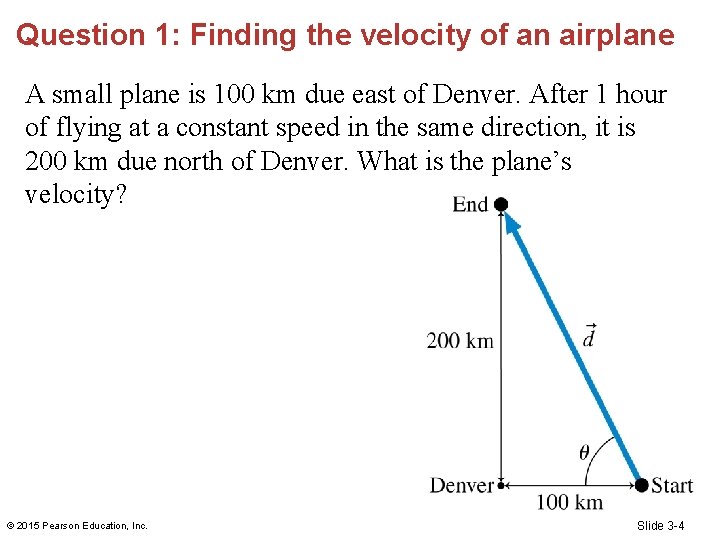
Question 1: Finding the velocity of an airplane A small plane is 100 km due east of Denver. After 1 hour of flying at a constant speed in the same direction, it is 200 km due north of Denver. What is the plane’s velocity? © 2015 Pearson Education, Inc. Slide 3 -4

Accelerated Motion

Acceleration • You can feel a difference between uniform (constant) and nonuniform (accelerated) motion. • When you move in a nonuniform motion, you feel pushed or pulled. • In contrast, when you are in uniform motion and your eyes are closed, you feel as though you are not moving at all.

Acceleration • So far, we’ve talked about “how far” and “how fast”…now we want to study “how fast an object is getting faster” • The rate at which an object’s velocity changes is called acceleration. • Acceleration is measured in m/s/s or m/s 2. • What is meant by “per”

Acceleration • Acceleration: is the rate at which velocity changes over time. • An object accelerates if its speed, direction, or both change. • Acceleration has direction and magnitude. • Thus, acceleration is a vector quantity.

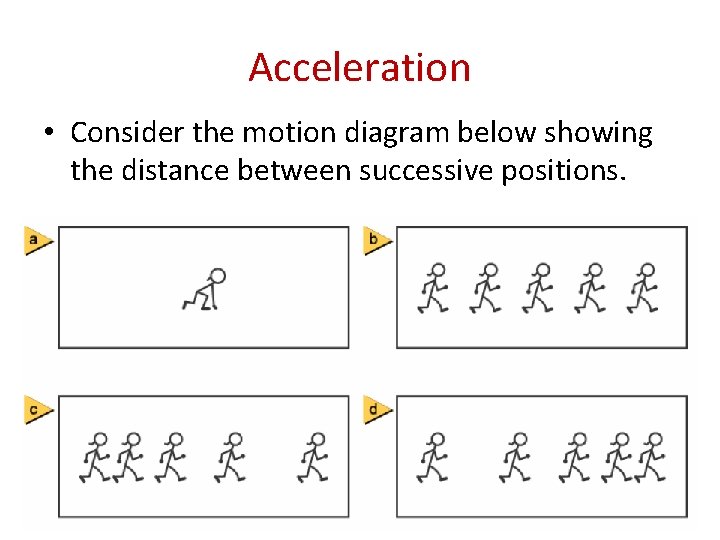
Acceleration • Consider the motion diagram below showing the distance between successive positions.

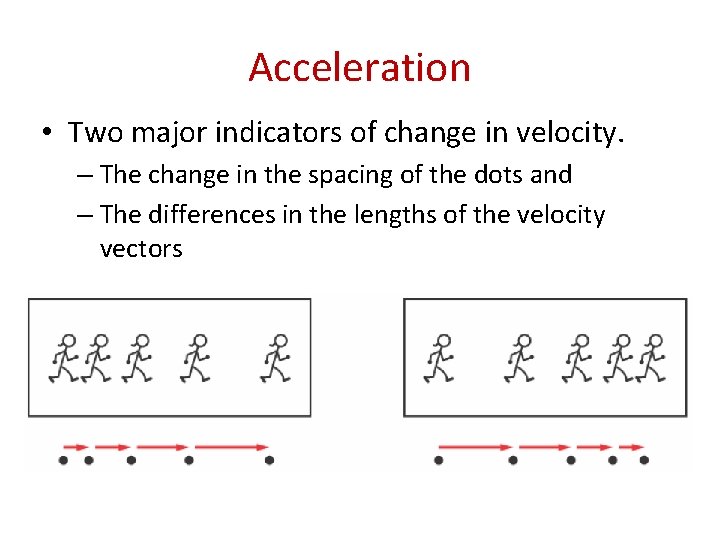
Acceleration • Two major indicators of change in velocity. – The change in the spacing of the dots and – The differences in the lengths of the velocity vectors

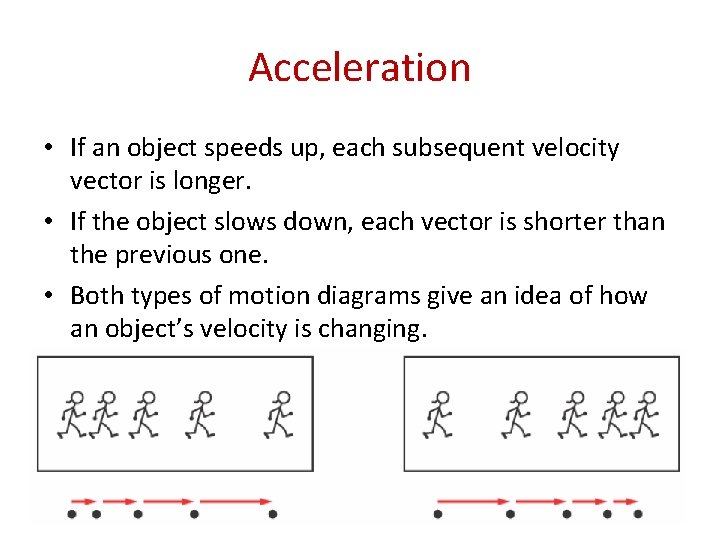
Acceleration • If an object speeds up, each subsequent velocity vector is longer. • If the object slows down, each vector is shorter than the previous one. • Both types of motion diagrams give an idea of how an object’s velocity is changing.

Displaying Acceleration on a Motion Diagram • To determine the length and direction of an average acceleration vector, • subtract two consecutive velocity vectors, as shown below. Slide 3 -12

Displaying Acceleration on a Motion Diagram • Direction: You will have: ∆v = vf - vi = vf + (-vi) Acceleration Vector Always the same as ∆ • Magnitude: Then divide by the time interval, ∆t. • Remember: Slide 3 -13

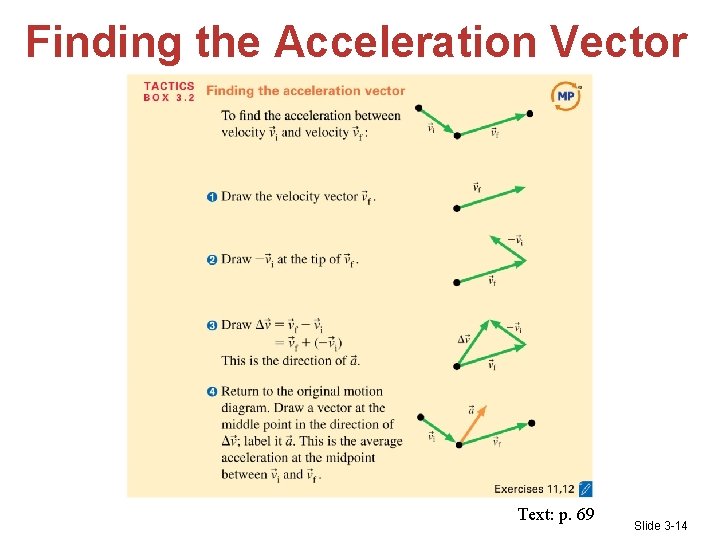
Finding the Acceleration Vector Text: p. 69 Slide 3 -14

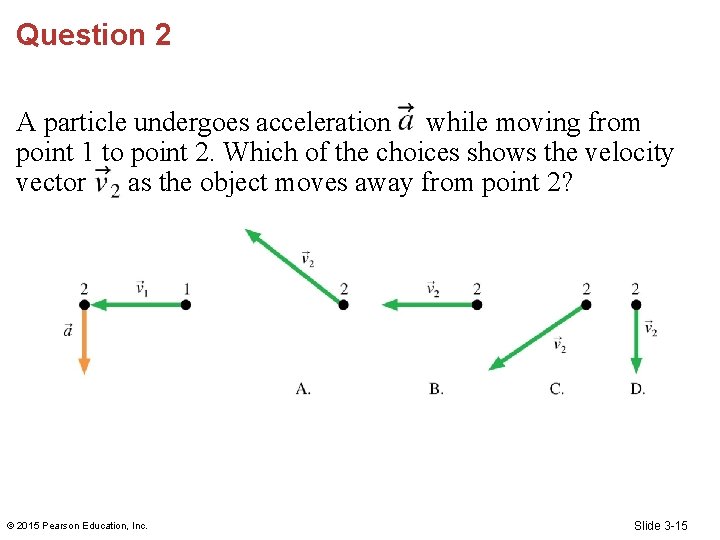
Question 2 A particle undergoes acceleration while moving from point 1 to point 2. Which of the choices shows the velocity vector as the object moves away from point 2? © 2015 Pearson Education, Inc. Slide 3 -15

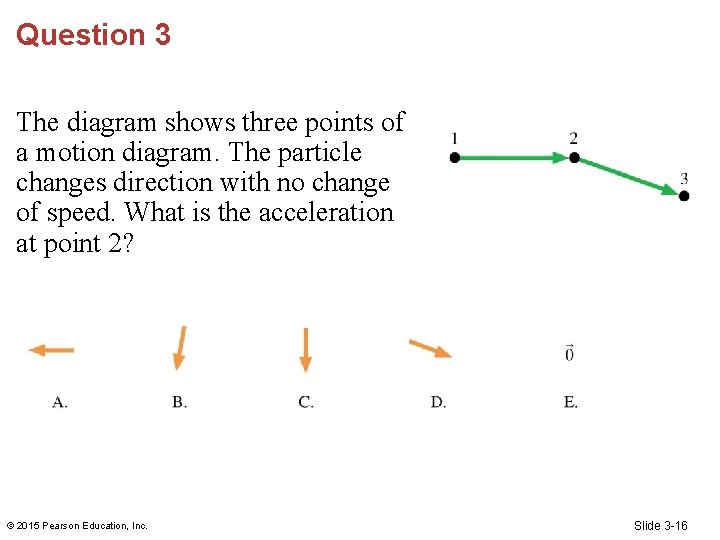
Question 3 The diagram shows three points of a motion diagram. The particle changes

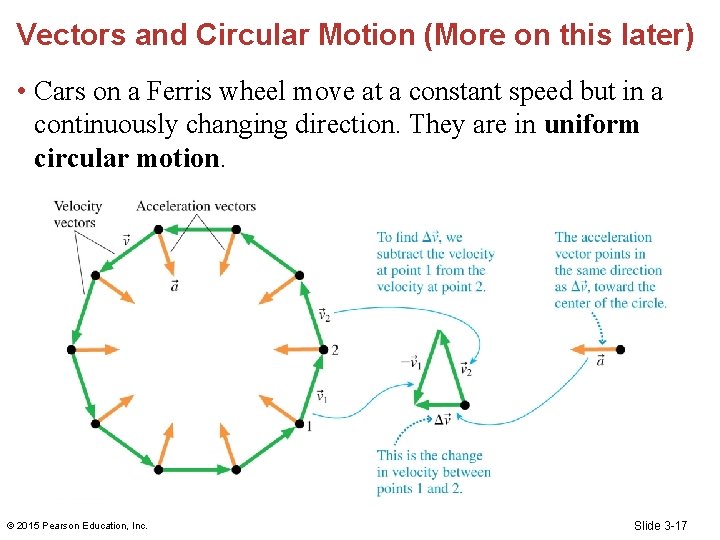
Vectors and Circular Motion (More on this later) • Cars on a Ferris wheel move at a constant speed but in a continuously changing direction. They are in uniform circular motion. © 2015 Pearson Education, Inc. Slide 3 -17

Position, Velocity, Acceleration Note: Constant Velocity =No Change in velocity ACCELERATION = 0

Positive and Negative Acceleration • When the object’s acceleration is in the same direction as its velocity, – the object’s velocity increases. • When they are in opposite directions, – the velocity decreases. • So……. . …

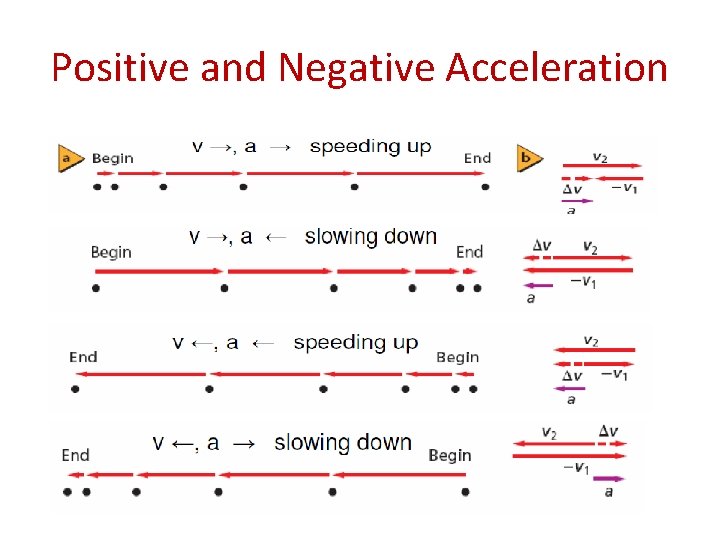
Positive and Negative Acceleration