ITI 1120 Lab 8 Contributors Diana Inkpen Daniel

ITI 1120 Lab #8 Contributors: Diana Inkpen, Daniel Amyot, Sylvia Boyd, Amy Felty, Romelia Plesa, Alan Williams

Lab 8 Agenda • Recursion – Examples of recursive algorithms – Recursive Java methods

Recursion Practice problem #1 • Write a recursive algorithm for counting the number of digits in a non-negative integer, N

Practice problem #1 - solution GIVENS: N INTERMEDIATE: Rest. Of. Digits RESULT: Count (the number of digits in N) HEADER: Count Number. Of. Digits(N)
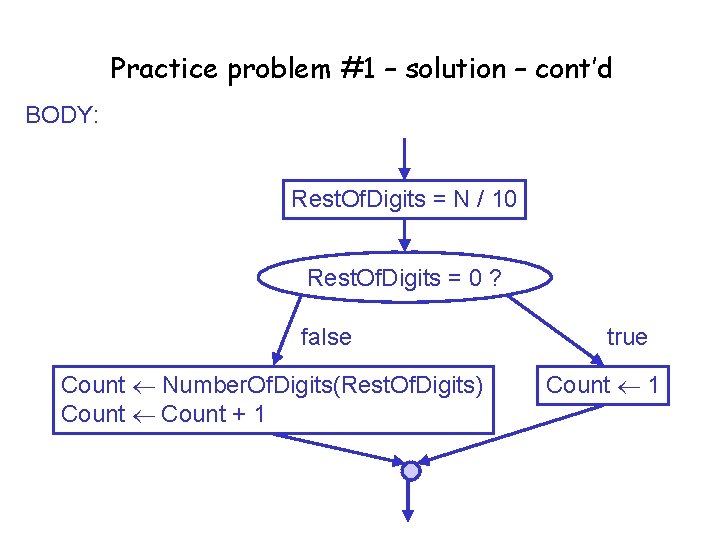
Practice problem #1 – solution – cont’d BODY: Rest. Of. Digits = N / 10 Rest. Of. Digits = 0 ? false Count Number. Of. Digits(Rest. Of. Digits) Count + 1 true Count 1

Trace for N = 254 Line Initial values (1) Rest. Of. Digits = N / 10 (2) Rest. Of. Digits = 0 ? false (3) CALL Count Number. Of. Digits(Rest. Of. Digits) (4) Count + 1 N Rest. Of. Digits Count 254 ? ? 25

Trace, page 2 Count Number. Of. Digits(Rest. Of. Digits) 25 Count Number. Of. Digits(N) Line N Rest. Of. Digits Count Initial values 25 ? ? (1) Rest. Of. Digits = N / 10 (2) Rest. Of. Digits = 0 ? false (3) CALL Count Number. Of. Digits(Rest. Of. Digits) (4) Count + 1 2

Trace , page 3 Count Number. Of. Digits(Rest. Of. Digits) 1 2 Count Number. Of. Digits(N) Line Initial values (1) Rest. Of. Digits = N / 10 N 2 Rest. Of. Digits ? 0 Count ? (2) Rest. Of. Digits = 0 ? true (5) Count 1 1
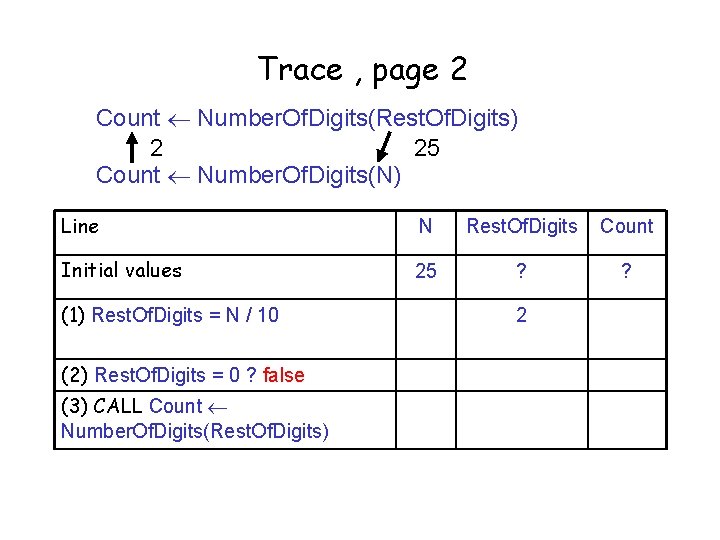
Trace , page 2 Count Number. Of. Digits(Rest. Of. Digits) 2 25 Count Number. Of. Digits(N) Line N Rest. Of. Digits Count Initial values 25 ? ? (1) Rest. Of. Digits = N / 10 2 (2) Rest. Of. Digits = 0 ? false (3) CALL Count Number. Of. Digits(Rest. Of. Digits) 1 (4) Count + 1 2
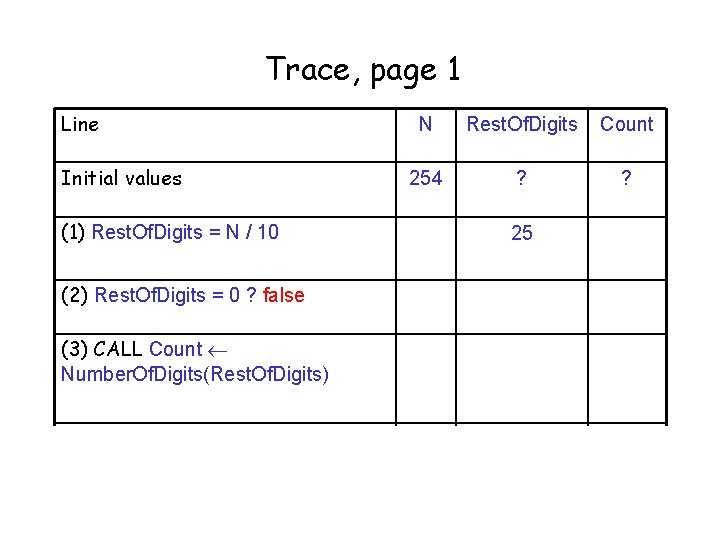
Trace, page 1 Line Initial values (1) Rest. Of. Digits = N / 10 N Rest. Of. Digits Count 254 ? ? 25 (2) Rest. Of. Digits = 0 ? false (3) CALL Count Number. Of. Digits(Rest. Of. Digits) 2 (4) Count + 1 3

Implement this algorithm in Java

Let’s see how the code runs • In your recursive method: • Put System. out. println() statements at the following locations (print the actual value of n): – Immediately after local variable declarations 1: Entering method with n = 254 – Just before recursive method call: 2: Recursive call from n = 254 – Just after recursive method call: 3: Returned from recursion with n = 254 – Just before return statement 4: Returning from method with n = 254, count = 3 – In the base case 5: Base case with n = 2

Practice problem #2 • Write a recursive algorithm to test if all the characters in positions 0. . . N-1 of an array, A, of characters are digits.

Practice problem #2 - solution GIVENS: A N RESULT: All. Digits (an array of characters) (test up to this position in array) (Boolean, true if all characters in position 0. . N are digits) HEADER: All. Digits Check. Digits(A, N)
![Practice problem #2 – solution – cont’d BODY: false A[N-1] ≥ ′ 0′ AND Practice problem #2 – solution – cont’d BODY: false A[N-1] ≥ ′ 0′ AND](http://slidetodoc.com/presentation_image_h2/6b777ded3dc69d008a2aec8fd60301b8/image-15.jpg)
Practice problem #2 – solution – cont’d BODY: false A[N-1] ≥ ′ 0′ AND A[N-1] ′ 9′ ? All. Digits False false true N=1? All. Digits Check. Digits(A, N-1) true All. Digits True

Practice problem #2 –– cont’d • Translate the algorithm into a Java method

Practice problem #2 – solution – cont’d

Practice problem #3 • Write a recursive algorithm to test if a given array is in sorted order.

Practice problem #3 - solution GIVENS: A N RESULT: Sorted (an array of integers) (the size of the array) (Boolean: true if the array is sorted) HEADER: Sorted Check. Sorted(A, N)
![Practice problem #3 – solution – cont’d BODY: false A[N– 2] < A[N– 1] Practice problem #3 – solution – cont’d BODY: false A[N– 2] < A[N– 1]](http://slidetodoc.com/presentation_image_h2/6b777ded3dc69d008a2aec8fd60301b8/image-20.jpg)
Practice problem #3 – solution – cont’d BODY: false A[N– 2] < A[N– 1] ? Sorted False N=1? true Sorted True Sorted Check. Sorted(A, N-1)

Practice problem #4 • Write a recursive algorithm to create an array containing the values 0 to N-1 • Hint: – Sometimes you need 2 algorithms: • The first is a “starter” algorithm that does some setup actions, and then starts off the recursion by calling the second algorithm • The second is a recursive algorithm that does most of the work.

Practice problem #4 - solution GIVENS: N (the size of the array) RESULT: A (the array) HEADER: A Create. Array(N) BODY: A Make. New. Array(N) Fill. Array(A, N – 1) Fill. Array is the recursive algorithm

Practice problem #4 – solution – cont’d Algorithm Fill. Array GIVENS: A (an array) N (the largest position in the array to fill) MODIFIEDS: A RESULT: (none) HEADER: Fill. Array(A, N)
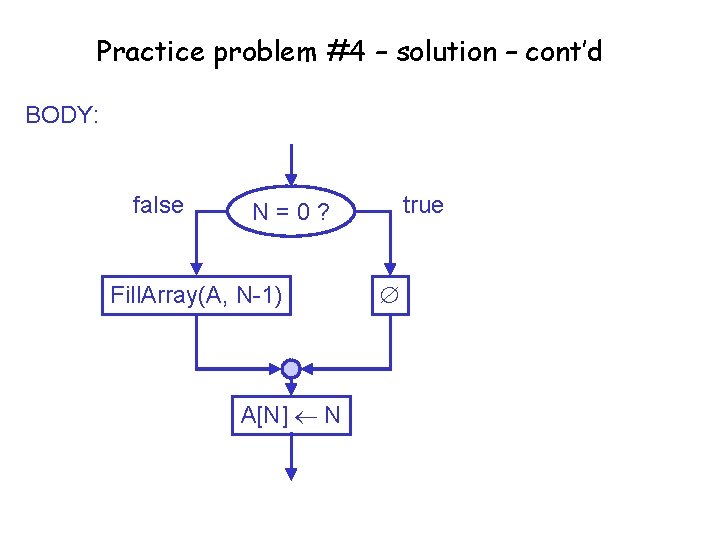
Practice problem #4 – solution – cont’d BODY: false true N=0? Fill. Array(A, N-1) A[N] N

Practice Problem #5: Euclid’s algorithm • The greatest common divisor (GCD) of two positive integers is the largest integer that divides both values with remainders of 0. • Euclid’s algorithm for finding the greatest common divisor is as follows: gcd(a, b) is … • b if a ≥ b and a mod b is 0 • gcd(b, a) if a < b • gcd(b, a mod b) otherwise • Write a recursive algorithm that takes two integers A and B and returns their greatest common divisor. You may assume that A and B are integers greater than or equal to 1.

What is the base case? Find. GCD(A, B) is … • B • Find. GCD(B, A) • Find. GCD(B, A MOD B) if A ≥ B and A MOD B is 0 if A < B otherwise • Question: will this algorithm always reach the base case? – Note that A MOD B is at most B – 1.

Euclid’s Algorithm GIVENS: A, B (Two integers > 0) RESULT: GCD (greatest common divisor of A and B) HEADER: GCD Find. GCD(A, B)
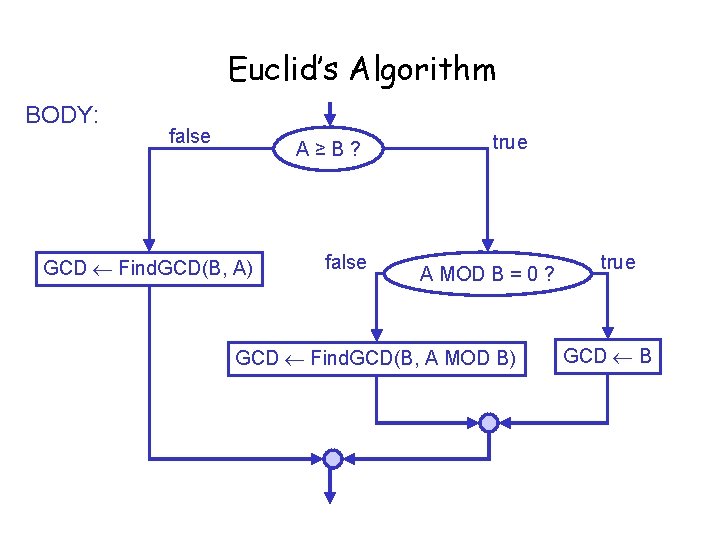
Euclid’s Algorithm BODY: false A≥B? GCD Find. GCD(B, A) false true A MOD B = 0 ? GCD Find. GCD(B, A MOD B) true GCD B

Euclid’s Algorithm in Java

Test this method • Create a class Euclid that includes the method find. GCD, and also a main( ) method that will ask the user to enter two values and print their GCD. • Try the following: a = 1234, b = 4321 a = 8192, b = 192
- Slides: 30