Iterators Revisited Proof Rules and Implementation Bart Jacobs

Iterators Revisited: Proof Rules and Implementation Bart Jacobs, Erik Meijer, Frank Piessens, Wolfram Schulte

Outline • Iterators in C# • How to specify and verify iterators and foreach loops? • How to prevent interference between iterators and foreach loops? • What are nested iterators? • How to implement nested iterators efficiently?

The Iterator pattern in C# 2. 0 public interface IEnumerator<T> { T Current { get; } bool Move. Next(); } public interface IEnumerable<T> { IEnumerator<T> Get. Enumerator(); }

Foreach Loops foreach (T x in C) S is implemented as IEnumerable<T> c = C; IEnumerator<T> e = c. Get. Enumerator(); while (e. Move. Next()) { T x = e. Current; S }

C# 2. 0 Iterator Methods IEnumerable<int> From. To(int a, int b) { for (int x = a; x < b; x++) yield return x; } is implemented as IEnumerable<int> From. To(int a, int b) { return new From. To_Enumerable(a, b); } Compiler-generated class

C# 2. 0 Iterator Methods class From. To_Enumerator : IEnumerator<int> { int a; int b; int pc; int x; int current; public From. To_Enumerator(int _a, int _b) { a = _a; b = _b; } public int Current { get { return current; } } public bool Move. Next() { switch (pc) { case 0: x = a; goto case 1; case 1: if (!(x < b)) goto case 4; case 2: current = x; pc = 3; return true; case 3: x++; goto case 1; case 4: pc = 4; return false; }}}

How to specify and verify iterators? static IEnumerable<int> From. To(int a, int b) requires a <= b; invariant forall{int i in (0; b – a); values[i] == a + i}; invariant values. Count <= b – a; ensures values. Count == b – a; { Enumeration invariant must be proved at start of iterator method… for (int x = a; x < b; x++) invariant values. Count == x – a; { yield return x; } … and after each yield return statement. } Ensures clause must be proved at end of method (and at yield break statements)

How to specify and verify foreach loops? int sum = 0; Seq<int> values = new Seq<int>(); while (*)(int x in From. To(1, 3)) foreach invariant sum == Math. Sum(values); free invariant forall{int i in (0: values. Count); values[i]==1+i}; free invariant values. Count <= 3 – 1; { int x; havoc x; values. Add(x); assume forall{int i in (0: values. Count); values[i]==1+i}; assume values. Count <= 3 – 1; sum += x; } assume values. Count == 3 – 1; assert sum == 6;
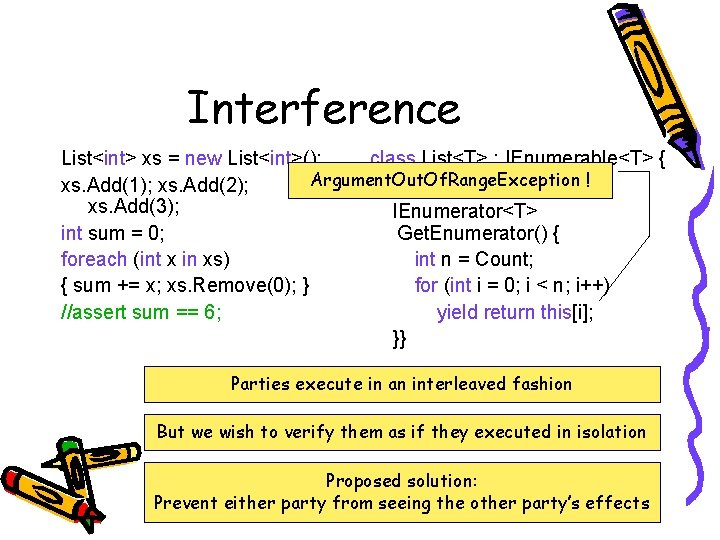
Interference List<int> xs = new List<int>(); class List<T> : IEnumerable<T> { Argument. Out. Of. Range. Exception ! xs. Add(1); xs. Add(2); … xs. Add(3); IEnumerator<T> int sum = 0; Get. Enumerator() { foreach (int x in xs) int n = Count; { sum += x; xs. Remove(0); } for (int i = 0; i < n; i++) //assert sum == 6; yield return this[i]; }} Parties execute in an interleaved fashion But we wish to verify them as if they executed in isolation Proposed solution: Prevent either party from seeing the other party’s effects
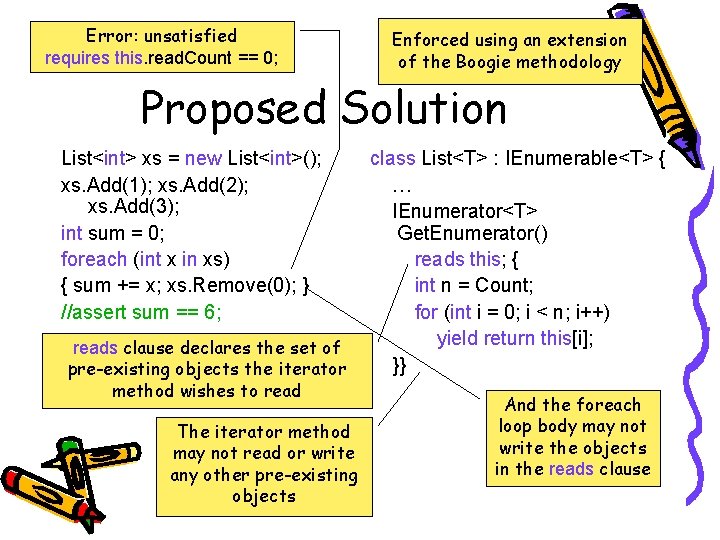
Error: unsatisfied requires this. read. Count == 0; Enforced using an extension of the Boogie methodology Proposed Solution List<int> xs = new List<int>(); xs. Add(1); xs. Add(2); xs. Add(3); int sum = 0; foreach (int x in xs) { sum += x; xs. Remove(0); } //assert sum == 6; reads clause declares the set of pre-existing objects the iterator method wishes to read The iterator method may not read or write any other pre-existing objects class List<T> : IEnumerable<T> { … IEnumerator<T> Get. Enumerator() reads this; { int n = Count; for (int i = 0; i < n; i++) yield return this[i]; }} And the foreach loop body may not write the objects in the reads clause

The Boogie methodology • Enforces object invariants • Uses a dynamic ownership system • Each object gets two extra fields: – bool inv; – bool writable; • o. f : = x; requires o. writable && !o. inv • unpack o; requires o. writable && o. inv – Sets o. inv : = false; – Makes owned objects writable • pack o; reverses the effect of unpack o;

Adding read-only objects to the Boogie methodology • Each object gets three special fields: – bool inv; – bool writable; – int read. Count; // never negative • o. f = x; requires o. writable && o. read. Count == 0 && !o. inv • x = o. f; requires o. writable || 0 < o. read. Count
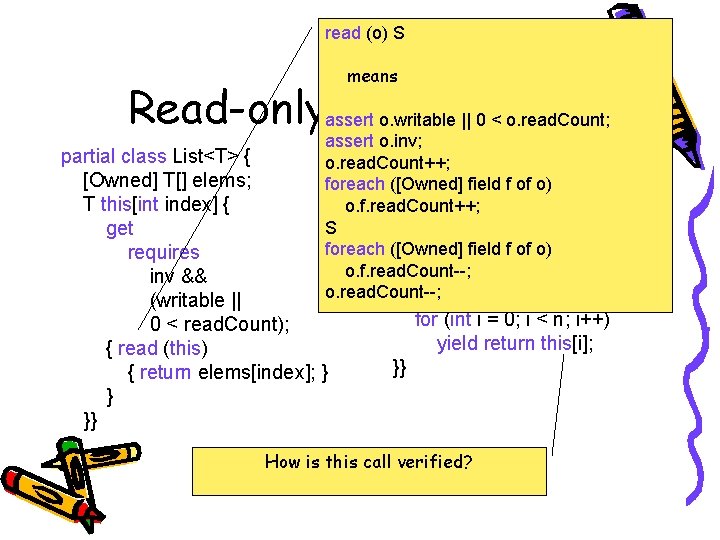
read (o) S means Read-onlyassert Methods o. writable || 0 < o. read. Count; assert o. inv; partial class List<T> : o. read. Count++; IEnumerable<T> foreach ([Owned] field f of o){ o. f. read. Count++; S IEnumerator<T> Get. Enumerator() foreach ([Owned] field f of o) o. f. read. Count--; reads this; { o. read. Count--; int n = Count; partial class List<T> { [Owned] T[] elems; T this[int index] { get requires inv && (writable || 0 < read. Count); { read (this) { return elems[index]; } } }} for (int i = 0; i < n; i++) yield return this[i]; }} How is this call verified?

General Approach to “Dependent Objects” • (Preliminary thoughts) • Each object has a set of dependee objects • Object may declare “dependent invariants” that dereference dependee objects • Dependent invariants become requires clauses, unless the dependent object is in Reader mode • Reader mode is statically nested within read blocks on dependee objects • Generic user of Iterator interface will require that Iterator object is in Reader mode

What are Nested Iterators? yield foreach E; means foreach (T x in E) yield return x; but is implemented with better time complexity if E evaluates to a nested iterator and with less garbage generation if E is a recursive call of the same iterator
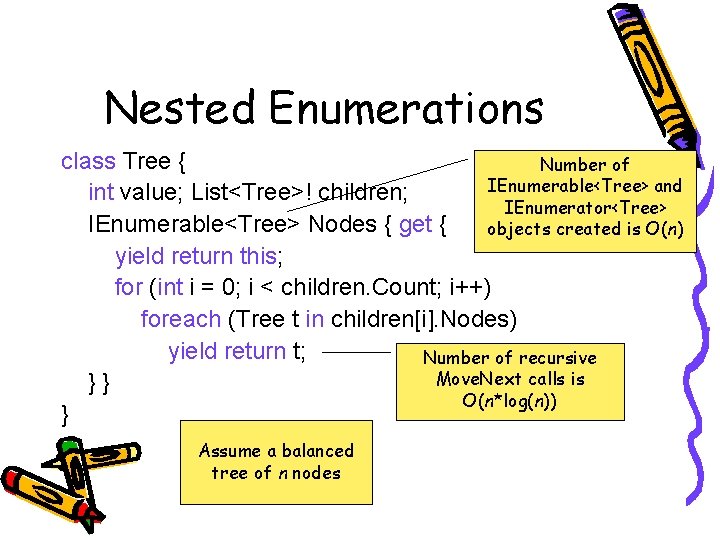
Nested Enumerations class Tree { Number of IEnumerable<Tree> and int value; List<Tree>! children; IEnumerator<Tree> IEnumerable<Tree> Nodes { get { objects created is O(n) yield return this; for (int i = 0; i < children. Count; i++) foreach (Tree t in children[i]. Nodes) yield return t; Number of recursive Move. Next calls is }} O(n*log(n)) } Assume a balanced tree of n nodes

Nested Iterators class Tree { int value; List<Tree>! children; IEnumerable<Tree> Nodes { get { yield return this; for (int i = 0; i < children. Count; i++) yield foreach children[i]. Nodes; }} }
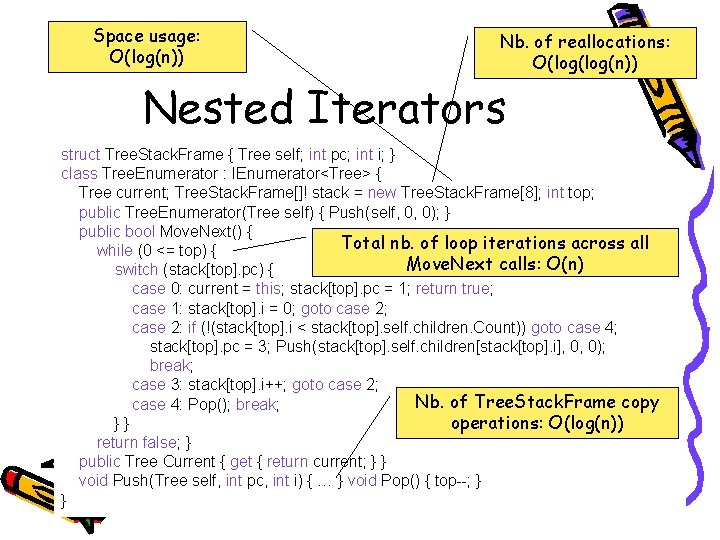
Space usage: O(log(n)) Nb. of reallocations: O(log(n)) Nested Iterators struct Tree. Stack. Frame { Tree self; int pc; int i; } class Tree. Enumerator : IEnumerator<Tree> { Tree current; Tree. Stack. Frame[]! stack = new Tree. Stack. Frame[8]; int top; public Tree. Enumerator(Tree self) { Push(self, 0, 0); } public bool Move. Next() { Total nb. of loop iterations across all while (0 <= top) { Move. Next calls: O(n) switch (stack[top]. pc) { case 0: current = this; stack[top]. pc = 1; return true; case 1: stack[top]. i = 0; goto case 2; case 2: if (!(stack[top]. i < stack[top]. self. children. Count)) goto case 4; stack[top]. pc = 3; Push(stack[top]. self. children[stack[top]. i], 0, 0); break; case 3: stack[top]. i++; goto case 2; Nb. of Tree. Stack. Frame copy case 4: Pop(); break; }} operations: O(log(n)) return false; } public Tree Current { get { return current; } } void Push(Tree self, int pc, int i) { … } void Pop() { top--; } }
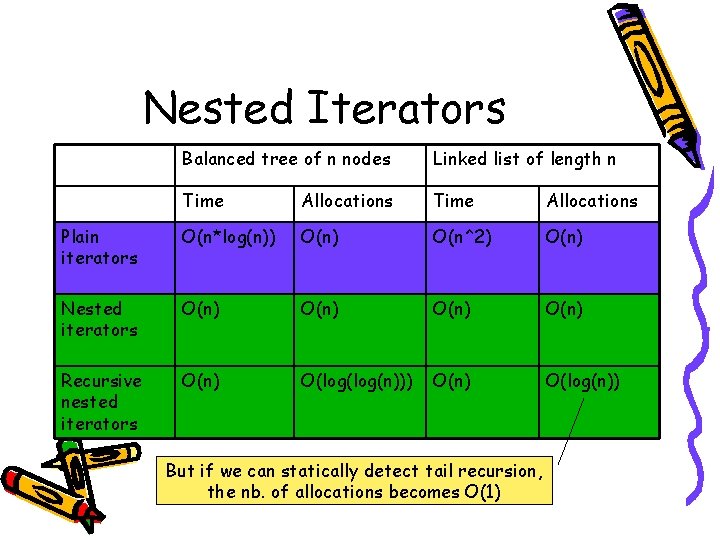
Nested Iterators Balanced tree of n nodes Linked list of length n Time Allocations Plain iterators O(n*log(n)) O(n^2) O(n) Nested iterators O(n) Recursive nested iterators O(n) O(log(n))) O(n) O(log(n)) But if we can statically detect tail recursion, the nb. of allocations becomes O(1)
- Slides: 19