Iterators Lists and Sequences Data Structures and Algorithms

Iterators, Lists, and Sequences Data Structures and Algorithms CS 244 Brent M. Dingle, Ph. D. Department of Mathematics, Statistics, and Computer Science University of Wisconsin – Stout Based on the book: Data Structures and Algorithms in C++ (Goodrich, Tamassia, Mount) Some content from Data Structures Using C++ (D. S. Malik)

Points of Note • Check assignment due dates • HW 08 due April 3 (today) • HW 09 due April 10

Last Time • Last class we talked about • Linked Lists • Dynamic Arrays • Book’s Vector ADT • The Vector ADT (§ 6. 1. 1) • Array-based implementation (§ 6. 1. 2) • Stacks • Queues • Dequeues

Today • Review: Iterators • Iterators (§ 6. 2. 5) mostly FYI • Lists and Sequences as ADTs • Position ADT (§ 6. 2. 1) mostly FYI • List ADT (§ 6. 2. 2) • Sequence ADT (§ 6. 3. 1) • Sorting

R ev ie w Iterators • Some functions supported by STL containers such as: – begin(), end() – return iterators to beginning or end of container – insert(I, e) – insert e just before the position indicated by iterator I – analogous to our linked list operation: insert. Before(p) – erase(I) – removes the element at the position indicated by I – analogous to our linked list operation: remove(p) • The functions can be used to insert/remove elements from arbitrary positions in the STL vector and list

Iterators Example • In the previous class there was an exercise that was based on the code: • Located at or near something like: • Content Unit 2 In. Class Examples Ex 225_Deque. With. Iters. cpp • Code example from this follows next slide

Iterator Example // typedef deque< char > my. Deque. Type; my. Deque. push_back( 'H' ); my. Deque. push_back( 'O' ); my. Deque. push_back( 'W' ); my. Deque. push_back( 'D' ); my. Deque. push_back( 'Y' ); //----------------------------------// Change them back but this time use iterators // instead of reference pointers. // Note how we dereference the iterators with * when setting them. my. Deque. Type: : iterator it_begin = my. Deque. begin(); my. Deque. Type: : iterator it_end = my. Deque. end(); *it_begin = 'H'; // Change the first element from h back to H --it_end; *it_end = 'Y'; // Change the last element from y to back to Y

Iterator Example 2 // typedef deque< char > my. Deque. Type; void print. Contents( my. Deque. Type deque ) { //----------------------------------// Using iterators, // which point to the beginning and ending of the vector, // loop through the vector and print out its contents my. Deque. Type: : iterator it_begin = deque. begin(); my. Deque. Type: : iterator it_end = deque. end(); cout << "Contents of my. Deque: "; } while (it_begin != it_end ) { cout << *it_begin << " " ; ++it_begin } cout << endl;

Group Class Activity • Create a program that instantiates a vector of integers using std: : vector • Then using a loop • Based on iterators begin() and end() • Pushes the Fibonacci numbers into the vector object • 1 1 2 3 5… • Starter Code can be found on D 2 L Circa: • Unit 2 In. Class Examples • GCA 210_Vector. Iterators. tar. gz • Submit the code to the correct D 2 L dropbox • 1 submission per “group” • Put all group member names in comments at top of main CPP file Forward and Backward

Lists and Sequences

FYI Background: Position ADT • The Position ADT models the notion of place within a data structure where a single object is stored – often in the sense of relative position • such as A is before B, or Z is after Y – also in the sense of first, second, third, … last • rather than just at index i • A special null position refers to no object. • Positions provide a unified view of diverse ways of storing data – a cell of an array – a node of a linked list • Member functions: – Object& element(): returns the element stored at this position – bool is. Null(): returns true if this is a null position

Book’s List ADT (§ 6. 2. 2) • The List ADT models a sequence of positions storing arbitrary objects – establishes a before/after relation between positions d e k n i l a is NOT his for insertion and • It. T allows removal in the “middle” t c a r t s b A a LIST s • Query It imethods: – is. First(p), is. Last(p) • Generic methods: – size(), is. Empty() • Accessor methods: – first(), last()ion t p i r c s e d list– before(p), after(p) e p y • DUpdate methods: T a t a – replace. Element(p, o), swap. Elements(p, q) – insert. Before(p, o), insert. After(p, o), – insert. First(o), insert. Last(o) – remove(p)

List ADT • Query methods: – is. First(p), is. Last(p) : • return boolean indicating if the given position is the first or last, respectively. • Accessor methods – first(), last(): • return the position of the first or last, resp. , element of S • an error occurs if S is empty S is the list – before(p), after(p): • return the position of the element of S preceding or following, respectively, the one at position p • an error occurs if S is empty, or p is the first or last, resp. , position

List ADT • Update Methods • replace. Element(p, o) • Replace the element at position p with e • swap. Elements(p, q) • Swap the elements stored at positions p & q • insert. Before(p, o), insert. After(p, o), • Insert a new element o into S before or after, resp. , position p • Output: position of the newly inserted element • insert. First(o), insert. Last(o) • Insert a new element o into S as the first or last, resp. , element • Output: position of the newly inserted element • remove(p) • Remove the element at position p from S S is the list

Class Exercises Follow • You are about to see 2 exercises • Mostly a compare and contrast exercise set • Think about run times too • This is a group discussion activity • Elect someone in your group to capture what is talked about in a MS-Word or text document • Randomly selected groups will present their findings at conclusion of each exercise

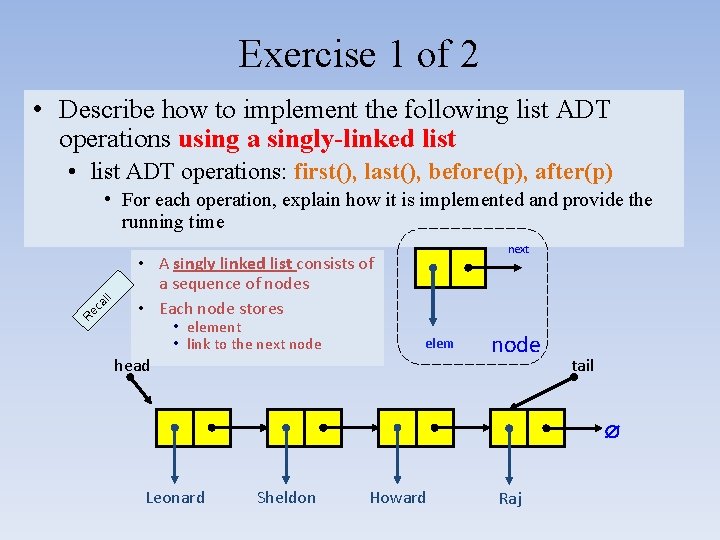
Exercise 1 of 2 • Describe how to implement the following list ADT operations using a singly-linked list • list ADT operations: first(), last(), before(p), after(p) R ec al l • For each operation, explain how it is implemented and provide the running time next • A singly linked list consists of a sequence of nodes • Each node stores • element • link to the next node elem head node tail Leonard Sheldon Howard Raj

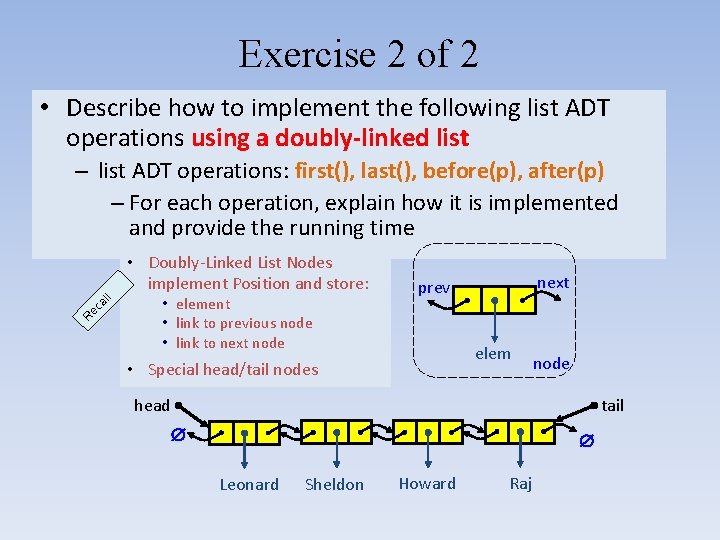
Exercise 2 of 2 • Describe how to implement the following list ADT operations using a doubly-linked list – list ADT operations: first(), last(), before(p), after(p) – For each operation, explain how it is implemented and provide the running time R ec al l • Doubly-Linked List Nodes implement Position and store: • element • link to previous node • link to next node next prev elem • Special head/tail nodes node tail head Leonard Sheldon Howard Raj

Enhanced Version Solution: Singly Linked List • In the implementation of the List ADT by means of a singly linked list • • The space used by a list with n elements is O(n) The space used by each position of the list is O(1) The before() operation runs in O(n) time All the other operations of the List ADT run in O(1) time

Enhanced Version Solution: Doubly Linked List • In the implementation of the List ADT by means of a doubly linked list • The space used by a list with n elements is O(n) • The space used by each position of the list is O(1) • All the operations of the List ADT run in O(1) time

Variances of Implementation • The details of implementing a list will vary • So STL implementation does not always match the book’s described ADT • This is common • So always check the interface description • wherever you may work

List Summary • List Operation Complexity for different implementations List Singly-Linked List Doubly- Linked first(), last(), after(p) insert. After(p, o), replace. Element(p, o), swap. Elements(p, q) O(1) before(p), insert. Before(p, o), remove(p) O(n) O(1) Size(), is. Empty() O(1)

Sequence ADT • The Sequence ADT is the union of • List-based methods: the Vector and List ADTs – first(), last(), before(p), • Elements accessed by after(p), – Rank, or replace. Element(p, o), – Position swap. Elements(p, q), • Generic methods: insert. Before(p, o), – size(), is. Empty() insert. After(p, o), • Vector-based methods: insert. First(o), – elem. At. Rank(r), replace. At. Rank(r, insert. Last(o), remove(p) o), insert. At. Rank(r, o), remove. At. Rank(r) • Bridge methods: – at. Rank(r), rank. Of(p)

Applications of Sequences • The Sequence ADT is a basic, general-purpose, data structure for storing an ordered collection of elements • Direct applications: • Generic replacement for stack, queue, vector, or list • small database (e. g. , address book) • Indirect applications: • Building block of more complex data structures

Sequence Implementations t! This is importan e differences th s e z ri a m m u s It and a List y a rr A n a n e e betw Operation size, is. Empty at. Rank, rank. Of, elem. At. Rank first, last, before, after replace. Element, swap. Elements replace. At. Rank insert. At. Rank, remove. At. Rank insert. First, insert. Last insert. After, insert. Before remove Array 1 1 1 List 1 n 1 1 1 n n 1 1 1

Outline and Reading • Where we are headed • Bubble Sort (§ 6. 4) • Merge Sort (§ 11. 1) • Summary of sorting algorithms

The End of This Part • Next • Bubble Sort and Merge Sort • Chapter 6 and 11. 1