Iterative Timing Recovery Aleksandar Kavi Division of Engineering

Iterative Timing Recovery Aleksandar Kavčić Division of Engineering and Applied Sciences Harvard University based on a tutorial by Barry, Kavčić, Mc. Laughlin, Nayak & Zeng And on research by Motwani and Kavčić DIMACS-04 Division of Engineering and Applied Sciences

Outline • • • Motivation Timing model Conventional timing recovery Simple iterative timing recovery Joint timing and intersymbol interference trellis Soft decision algorithm Performance results Conclusion Future challenge: capacity of channels with synchronization error slide 2 Division of Engineering and Applied Sciences

Motivation • In most communications (decoding) scenarios, we assume perfect timing recovery • This assumption breaks down, particularly at low signal-to-noise ratios (SNRs) • But, turbo-like codes work exactly at these SNRs • Need to take timing uncertainty into account slide 3 Division of Engineering and Applied Sciences

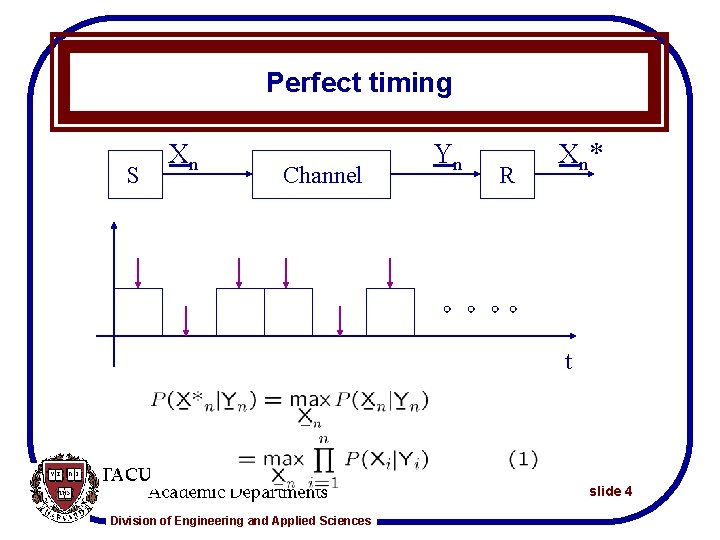
Perfect timing S Xn Channel Yn R Xn* t slide 4 Division of Engineering and Applied Sciences

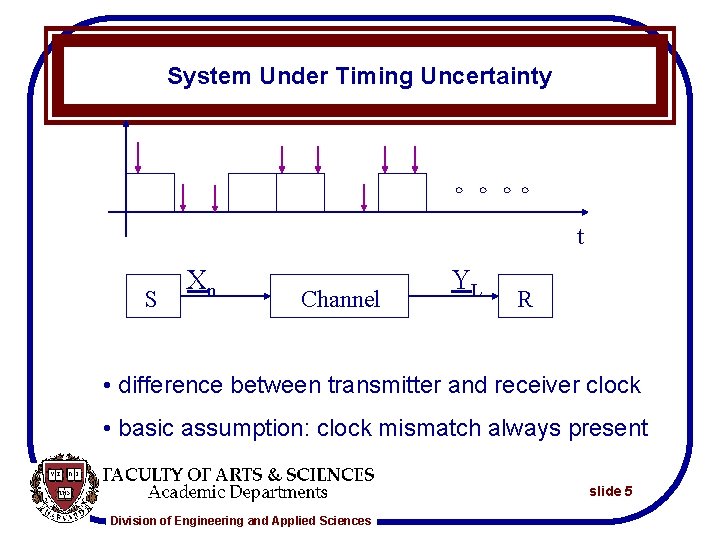
System Under Timing Uncertainty t S Xn Channel YL R • difference between transmitter and receiver clock • basic assumption: clock mismatch always present slide 5 Division of Engineering and Applied Sciences

A More Realistic Case 1 -T 0 T 2 T 3 T Sample instants: k. T+ k Division of Engineering and Applied Sciences t slide 6

Properties of the timing error t t • Brownian Motion Process (slow varying). • Discrete samples form a Markov chain. slide 7 Division of Engineering and Applied Sciences

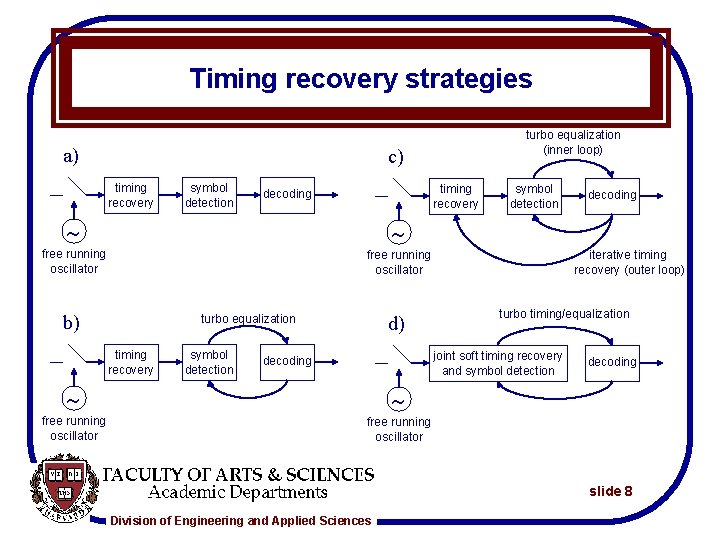
Timing recovery strategies a) turbo equalization (inner loop) c) timing recovery symbol detection timing recovery decoding free running oscillator b) d) turbo equalization timing recovery symbol detection iterative timing recovery (outer loop) turbo timing/equalization joint soft timing recovery and symbol detection decoding free running oscillator decoding slide 8 Division of Engineering and Applied Sciences

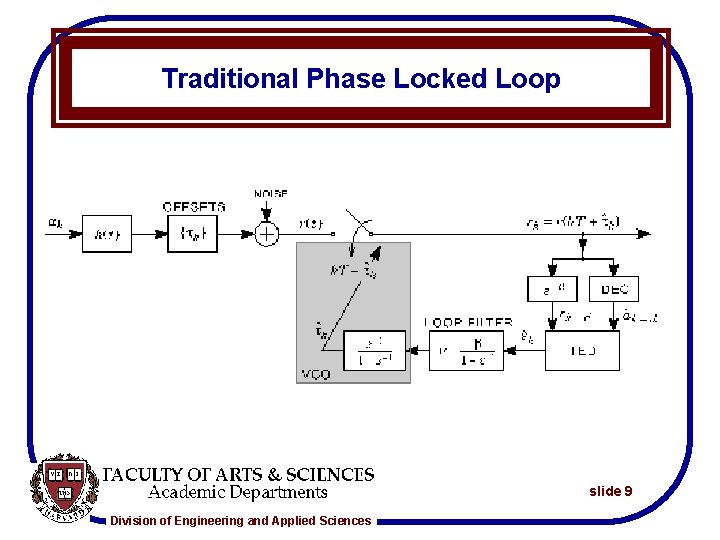
Traditional Phase Locked Loop slide 9 Division of Engineering and Applied Sciences

Simplest iterative timing reovery slide 10 Division of Engineering and Applied Sciences

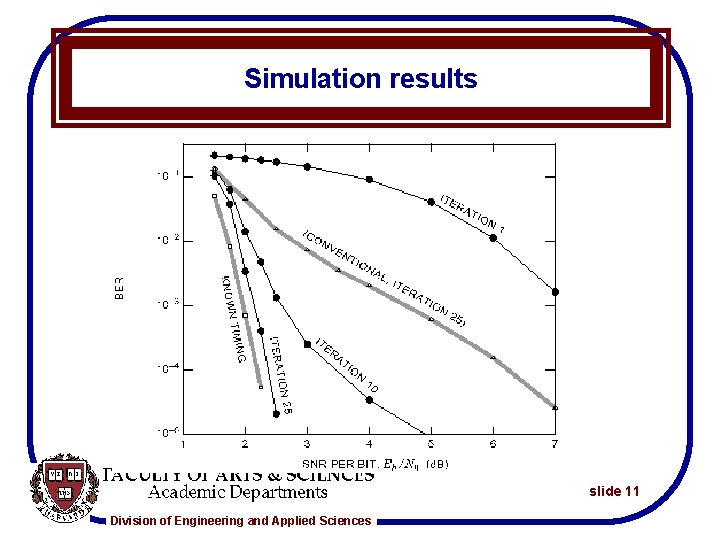
Simulation results slide 11 Division of Engineering and Applied Sciences

Convergence speed slide 12 Division of Engineering and Applied Sciences

Strategy to solve the problem 1. 2. 3. 4. Set up math model for timing error (Markov). Build separate stationary trellis to characterize the channel and source. Form a full trellis. Derive an algorithm to perform the Maximum a posteriori probability (MAP) estimation of the timing offset and the input bits slide 13 Division of Engineering and Applied Sciences

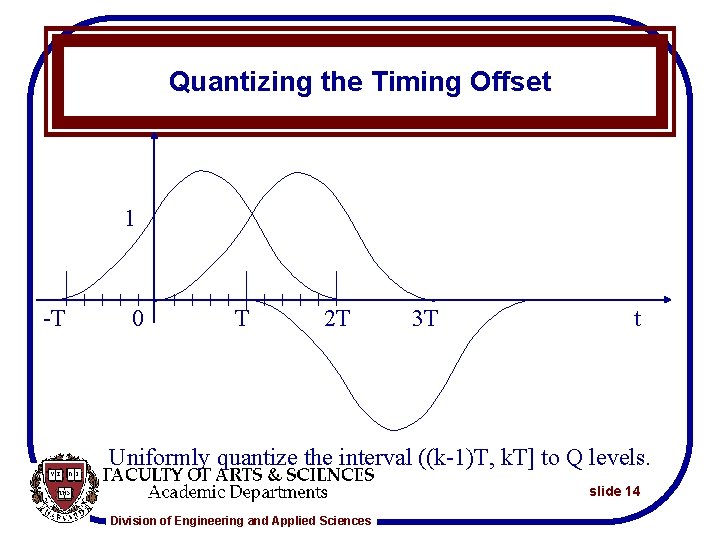
Quantizing the Timing Offset 1 -T 0 T 2 T 3 T t Uniformly quantize the interval ((k-1)T, k. T] to Q levels. slide 14 Division of Engineering and Applied Sciences

Math Model for Timing Error State Transition Diagram: δ -2θ -θ 0 θ 2θ δ State Transition Probability: slide 15 Division of Engineering and Applied Sciences

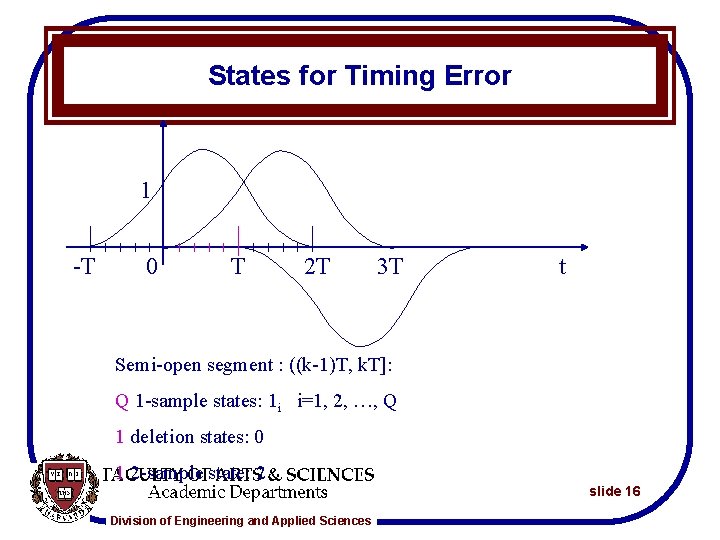
States for Timing Error 1 -T 0 T 2 T 3 T t Semi-open segment : ((k-1)T, k. T]: Q 1 -sample states: 1 i i=1, 2, …, Q 1 deletion states: 0 1 2 -sample state: 2 Division of Engineering and Applied Sciences slide 16

Example: timing error realization k Q=5 T/Q 0 -T/Q -2 T/Q -3 T/Q -4 T/Q -5 T/Q = -T 4 0 1 2 5 6 3 7 8 9 10 11 12 13 14 15 k slide 17 Division of Engineering and Applied Sciences

0 T 2 T 3 T 4 T 5 T 6 T 7 T 8 T 9 T 10 T 0 th 1 st 2 nd 3 rd 4 th 5 th 6 th 7 th 8 th 9 th 10 th interval interval interval 15 15 14 14 15 0 2 0 11 11 12 t 0 - 0 0 11 12 13 14 15 2 T- 1 2 T- 2 3 T- 3 4 T- 4 5 T- 5 6 T- 6 7 T- 7 8 T- 8 9 T- 9

Single trellis section 0 0 11 12 13 14 15 2 slide 19 Division of Engineering and Applied Sciences

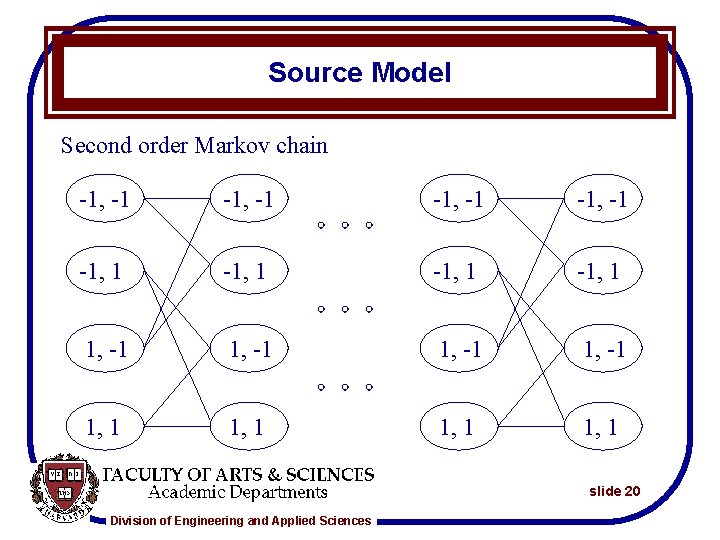
Source Model Second order Markov chain -1, -1 -1, 1 1, -1 1, 1 slide 20 Division of Engineering and Applied Sciences

Full Trellis Full states set: Total number of states at each time interval: Trellis length = n (block length). (note that each branch may have different number of outputs). slide 21 Division of Engineering and Applied Sciences

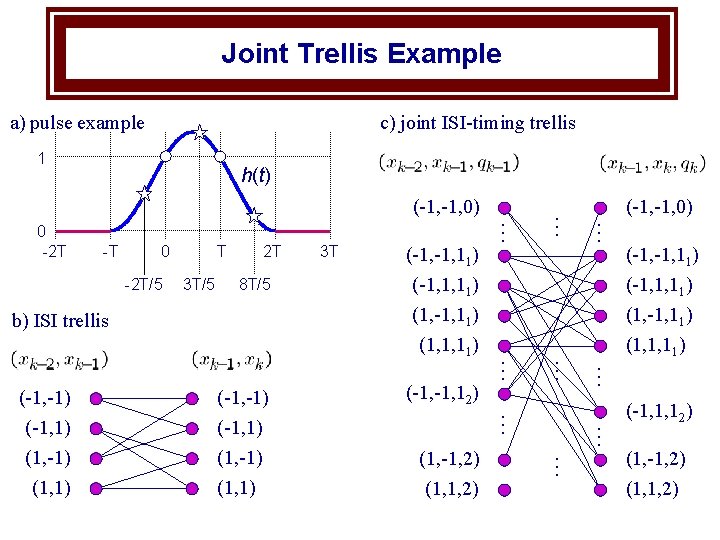
Joint Trellis Example a) pulse example c) joint ISI-timing trellis 1 h(t) 0 -2 T/5 T 3 T/5 2 T (-1, 11) (-1, 1, 12) … … (1, -1, 2) (1, 1, 2) … (-1, 12) … (-1, -1) (-1, 1) (1, -1) (1, 1) (-1, 11) (-1, 1, 11) (1, -1, 11) (1, 1, 11) … 8 T/5 b) ISI trellis (-1, -1) (-1, 1) (1, -1) (1, 1) 3 T (-1, 0) … -T … 0 -2 T … (-1, 0) (1, -1, 2) (1, 1, 2)

Soft-Output Detector slide 23 Division of Engineering and Applied Sciences

Definition of Some Functions Notation: Definition: slide 24 Division of Engineering and Applied Sciences

Calculation of the Soft-outputs slide 25 Division of Engineering and Applied Sciences

Recursion of α(t, m, i) slide 26 Division of Engineering and Applied Sciences

Recursion of β(t, m, i) slide 27 Division of Engineering and Applied Sciences

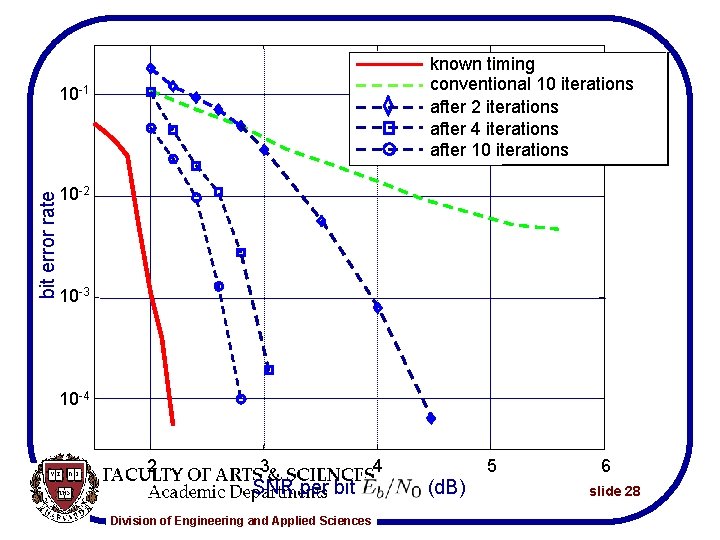
known timing conventional 10 iterations after 2 iterations after 4 iterations after 10 iterations bit error rate 10 -1 10 -2 10 -3 10 -4 2 3 SNR per bit Division of Engineering and Applied Sciences 4 5 (d. B) 6 slide 28

Cycle-slip correction results timing error T true timing error estimate after 1 iteration timing error estimate after 2 iterations timing error estimate after 3 iterations 0 -T -2 T 1000 2000 3000 4000 5000 time slide 29 Division of Engineering and Applied Sciences

Conclusion • Conventional timing recovery fails at low SNR because it ignores the error-correction code. • Iterative timing recovery exploits the power of the code. • Performance close to perfect timing recovery • Only marginal increase in complexity compared to system that uses conventional turbo equalization/decoding slide 30 Division of Engineering and Applied Sciences

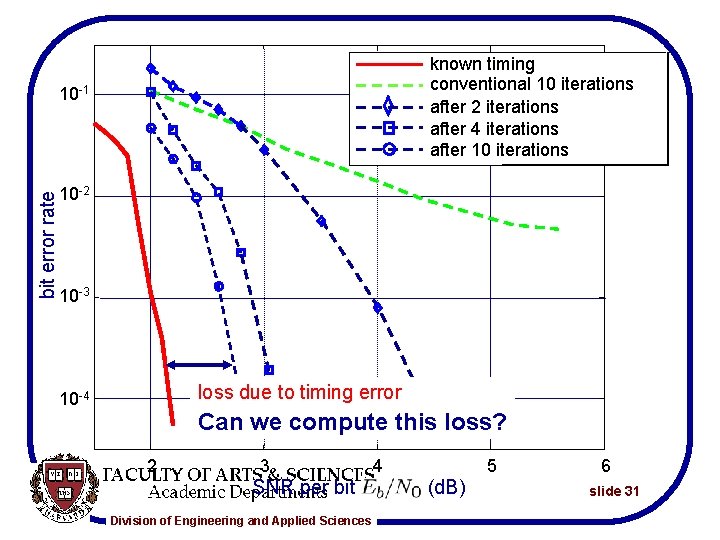
known timing conventional 10 iterations after 2 iterations after 4 iterations after 10 iterations bit error rate 10 -1 10 -2 10 -3 loss due to timing error 10 -4 Can we compute this loss? 2 3 SNR per bit Division of Engineering and Applied Sciences 4 5 (d. B) 6 slide 31

Open Problems • Information Theory for channels with synchronization error: – Capacity achieving distribution – Capacity achieving codes slide 32 Division of Engineering and Applied Sciences

Deletion channels • Transmitted sequence x 1, x 2, x 3, …. – Xk { 0, 1 } • Received sequence y 1, y 2, y 3, …. – Sequence y is a subsequence of sequence x • Symbol xk is deleted with probability slide 33 Division of Engineering and Applied Sciences

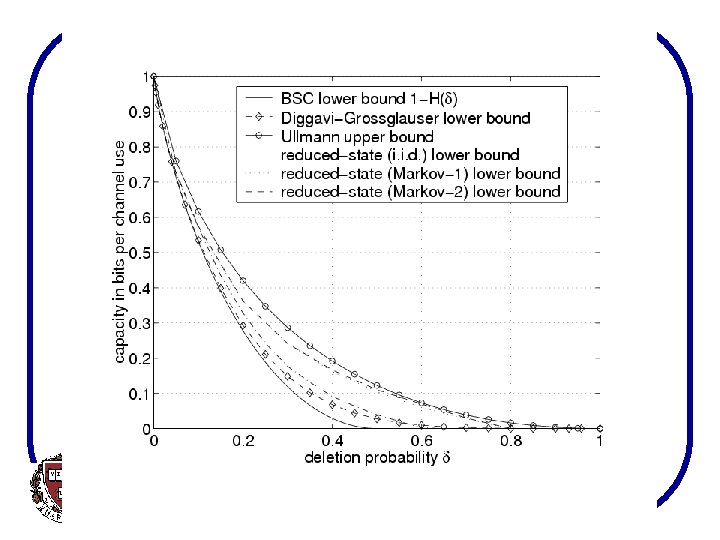
Deletion channels • Some results: – Ulmann 1968, upper bounds on the capacities of deletion channels – Diggavi&Grossglauser 2002, analytic lower bounds on capacities of deletion channels – Mitzenmacher 2004, tighter analytic lower bounds slide 34 Division of Engineering and Applied Sciences

slide 35 Division of Engineering and Applied Sciences

Numerical capacity computation methods slide 36 Division of Engineering and Applied Sciences

Received symbols per transmitted symbol Let K(m) denote the number of received symbols per m transmitted symbols K(m) is a random variable Asymptotically, we have A received symbols per transmitted symbol For the deletion channel, slide 37 Division of Engineering and Applied Sciences

Capacity per transmitted symbol compute upper bound slide 38 Division of Engineering and Applied Sciences

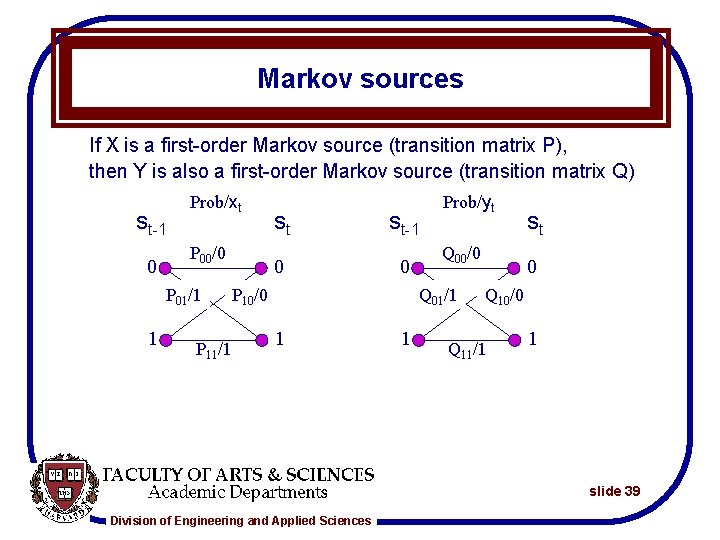
Markov sources If X is a first-order Markov source (transition matrix P), then Y is also a first-order Markov source (transition matrix Q) st-1 0 Prob/xt P 00/0 P 01/1 1 P 11/1 st 0 st-1 0 P 10/0 Prob/yt Q 00/0 Q 01/1 1 1 st 0 Q 10/0 Q 11/1 1 slide 39 Division of Engineering and Applied Sciences

Trellis for s 0 0 Prob/y 1 s 1 11 (1 - )/1 Prob/y 2 s 2 02 (1 - )/0 … (1 - ) /0 02 (1 - )/0 03 03 (1 - ) 2/1 (1 - ) 2/0 (1 - )/1 … 14 Run a reduced-state BCJR algorithm on tis trellis to upper-bound H(Y|X) … (1 - ) 3/1 (1 - ) /1 14 Y|X 15 … … … Division of Engineering and Applied Sciences slide 40

slide 41 Division of Engineering and Applied Sciences

Future research • Upper bounds for insertion/deletion channels? • Channels with non-integer timing error? • Codes? (long run-lengths are favored in deletion channels) slide 42 Division of Engineering and Applied Sciences