Iterative Hard Thresholding for SparseLowrank Linear Regression Prateek






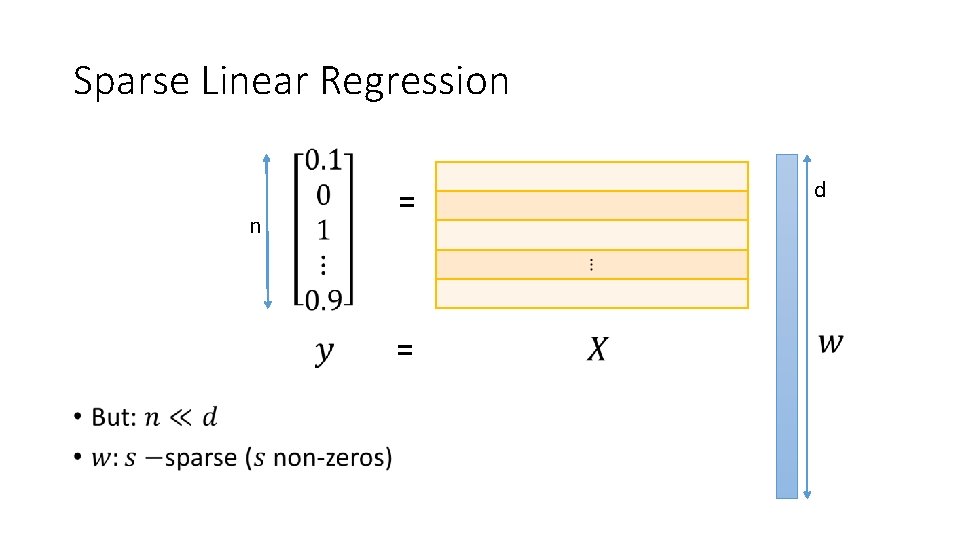


![Our Approach : Projected Gradient Descent • [Jain, Tewari, Kar’ 2014] Our Approach : Projected Gradient Descent • [Jain, Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-11.jpg)





![Statistical Guarantees • Same as Lasso [J. , Tewari, Kar’ 2014] Statistical Guarantees • Same as Lasso [J. , Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-20.jpg)
![General Result for Any Function • [J. , Tewari, Kar’ 2014] General Result for Any Function • [J. , Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-21.jpg)
![Extension to other Non-convex Procedures • IHT-Fully Corrective • HTP [Foucart’ 12] • Co. Extension to other Non-convex Procedures • IHT-Fully Corrective • HTP [Foucart’ 12] • Co.](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-22.jpg)


![Statistical Guarantees • [J. , Tewari, Kar’ 2014] Statistical Guarantees • [J. , Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-28.jpg)

![Guarantees • [J. , Netrapalli’ 2015] Guarantees • [J. , Netrapalli’ 2015]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-30.jpg)





- Slides: 35

Iterative Hard Thresholding for Sparse/Low-rank Linear Regression Prateek Jain Microsoft Research, India Ambuj Tewari Univ of Michigan Purushottam Kar MSR, India Praneeth Netrapalli MSR, NE

Microsoft Research India Our work • Foundations • Systems • Applications • Interplay of society and technology • Academic and government outreach Our vectors of impact • Research impact • Company impact • Societal impact

Machine Learning and Optimization @ MSRI • High-dimensional Learning & Optimization Manik Varma Prateek Jain Ravi Kannan Amit Deshpande Navin Goyal Sundarajan S. Vinod Nair Sreangsu Acharyya Kush Bhatia Aditya Nori Raghavendra Udupa Purushottam Kar • Extreme Classification • Online Learning / Multi-armed Bandits • Learning with Structured Losses We are Hiring! • • Interns • Distributed Machine Learning Post. Docs • Probabilistic Programming Applied Researchers • Privacy Preserving Machine Learning Full-time Researchers • SVMs & Kernel Learning • Ranking & Recommendation

Learning in High-dimensions 2 2 • • Non-convex • Complexity: NP-Hard

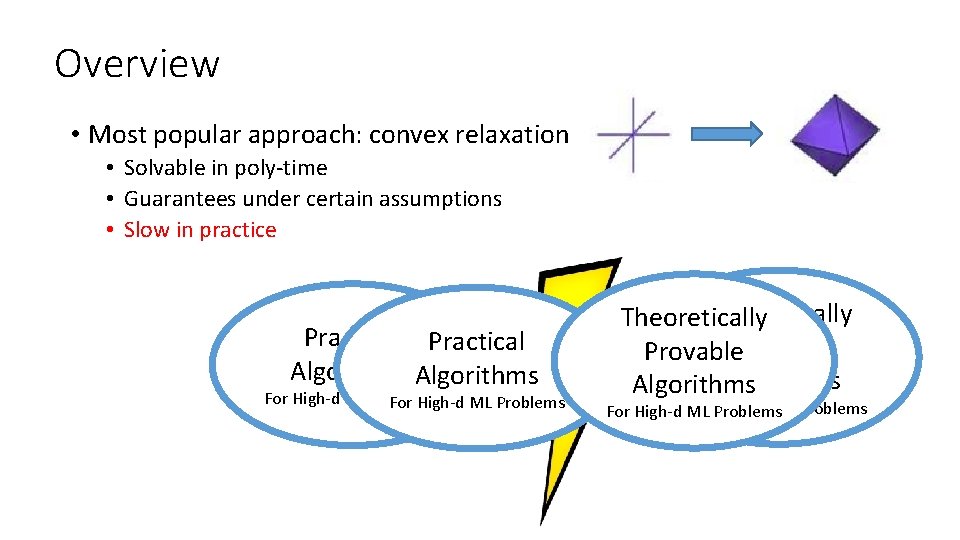
Overview • Most popular approach: convex relaxation • Solvable in poly-time • Guarantees under certain assumptions • Slow in practice Practical Algorithms For High-d ML Problems Theoretically Provable Algorithms For High-d ML Problems

Results • 6

Outline • Sparse Linear Regression • Lasso • Iterative Hard Thresholding • Our Results • Low-rank Matrix Regression • Low-rank Matrix Completion • Conclusions
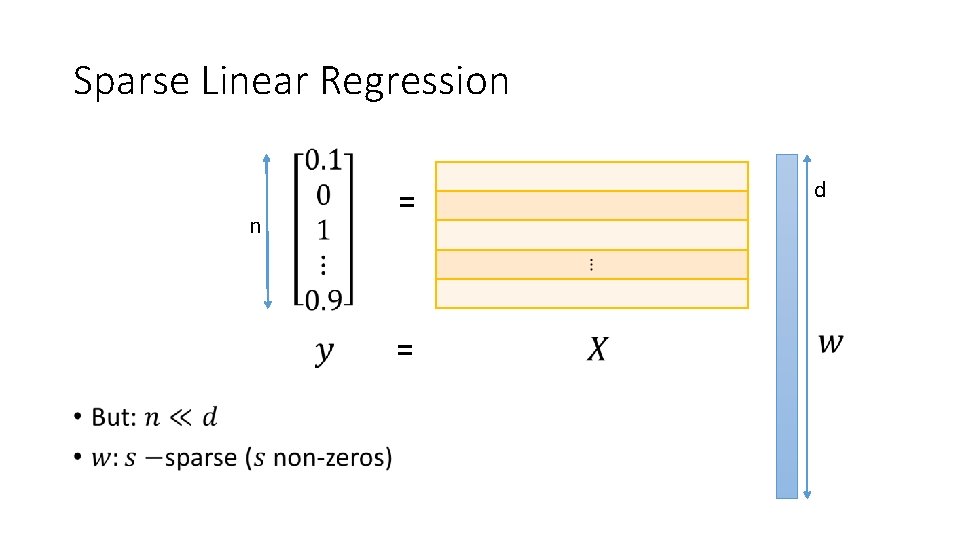
Sparse Linear Regression n d = =

Sparse Linear Regression •

Convex Relaxation • Non-differentiable Lasso Problem
![Our Approach Projected Gradient Descent Jain Tewari Kar 2014 Our Approach : Projected Gradient Descent • [Jain, Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-11.jpg)
Our Approach : Projected Gradient Descent • [Jain, Tewari, Kar’ 2014]

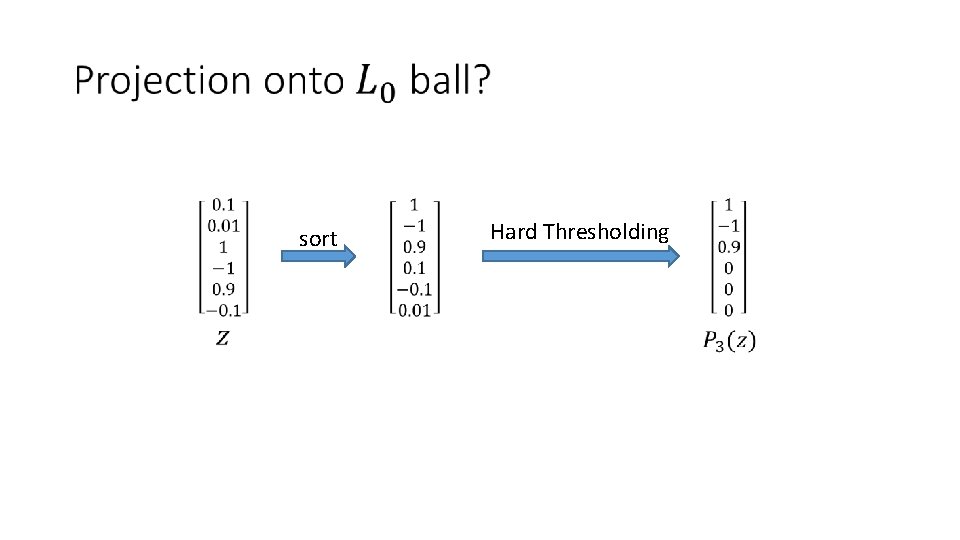
sort Hard Thresholding

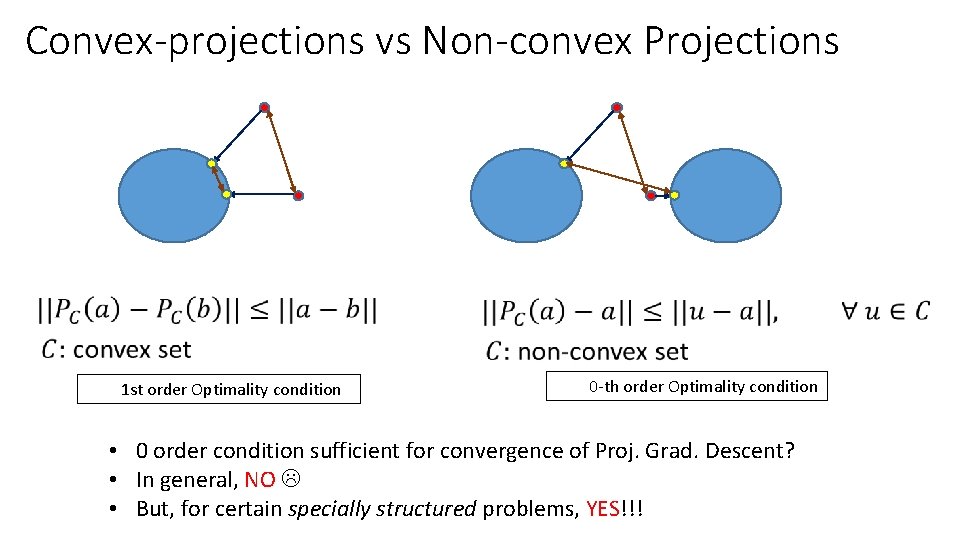
Convex-projections vs Non-convex Projections • 1 st order Optimality condition 0 -th order Optimality condition • 0 order condition sufficient for convergence of Proj. Grad. Descent? • In general, NO • But, for certain specially structured problems, YES!!!

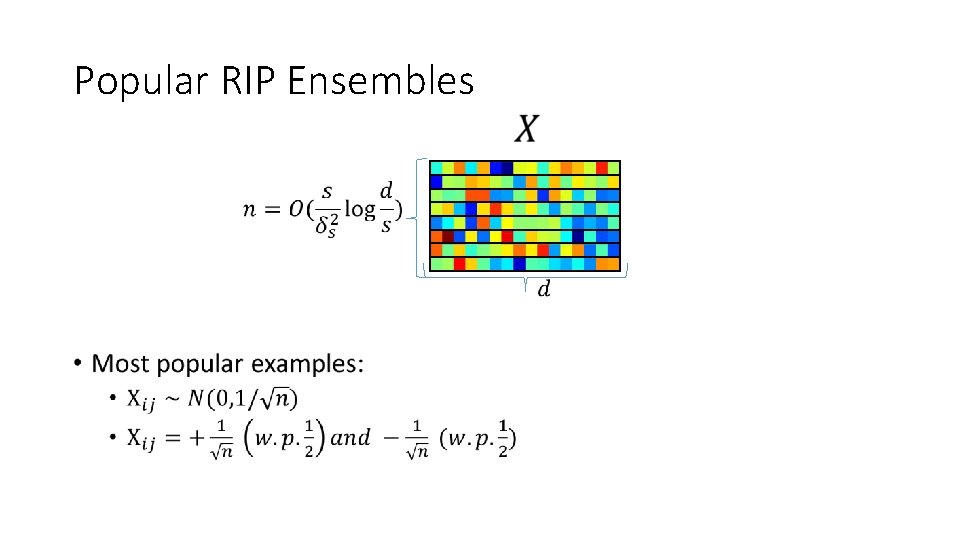
Restricted Isometry Property (RIP) •

Popular RIP Ensembles •

Proof under RIP • Hard Thresholding Triangle inequality RIP [Blumensath & Davies’ 09, Garg & Khandekar’ 09]

What if RIP is not possible? •

Iterative Hard Thresholding: Larger Sparsity •

Stronger Projection Guarantee •
![Statistical Guarantees Same as Lasso J Tewari Kar 2014 Statistical Guarantees • Same as Lasso [J. , Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-20.jpg)
Statistical Guarantees • Same as Lasso [J. , Tewari, Kar’ 2014]
![General Result for Any Function J Tewari Kar 2014 General Result for Any Function • [J. , Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-21.jpg)
General Result for Any Function • [J. , Tewari, Kar’ 2014]
![Extension to other Nonconvex Procedures IHTFully Corrective HTP Foucart 12 Co Extension to other Non-convex Procedures • IHT-Fully Corrective • HTP [Foucart’ 12] • Co.](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-22.jpg)
Extension to other Non-convex Procedures • IHT-Fully Corrective • HTP [Foucart’ 12] • Co. SAMP [Tropp & Neadell’ 2008] • Subspace Pursuit [Dai & Milenkovic’ 2008] • OMPR [J. , Tewari, Dhillon’ 2010] • Partial hard thresholding and two-stage family [J. , Tewari, Dhillon’ 2010]

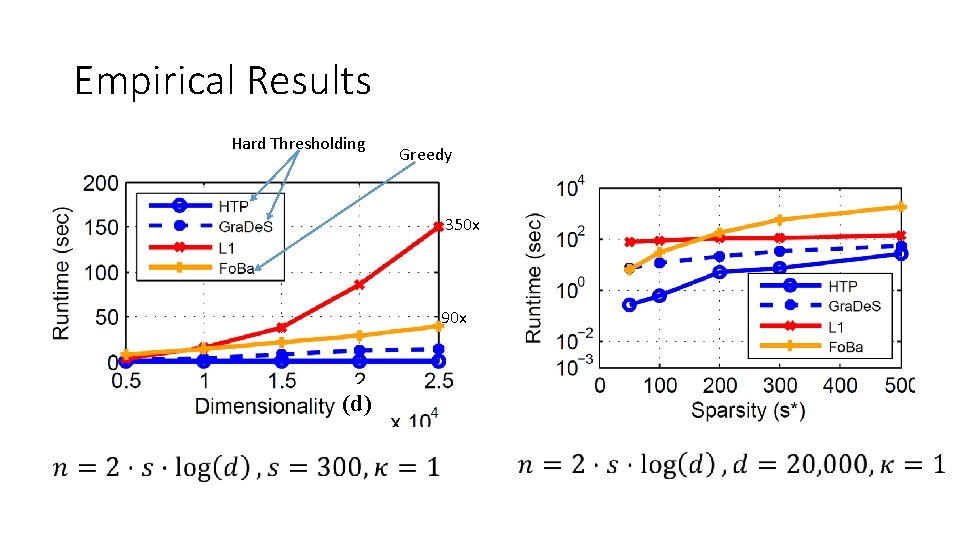
Empirical Results Hard Thresholding Greedy 350 x 90 x (d)

More Empirical Results

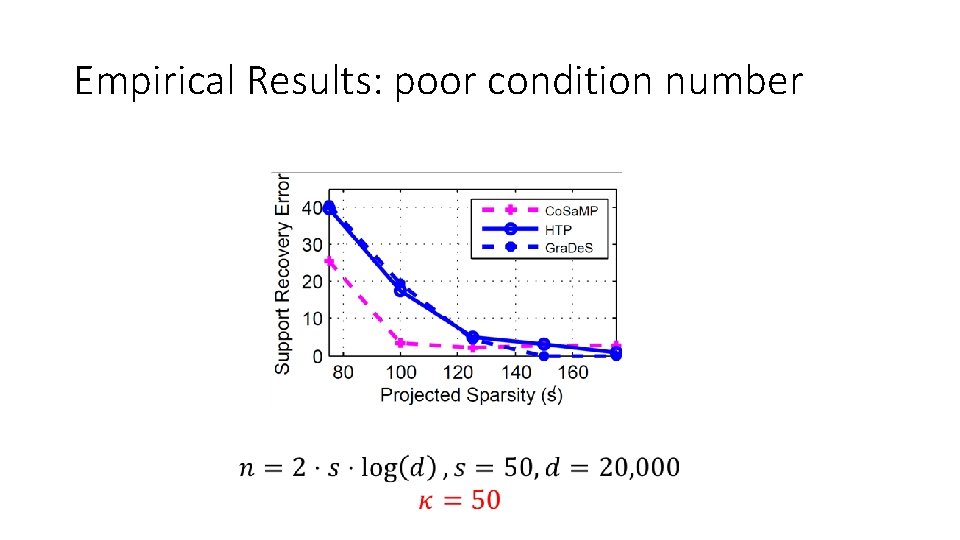
Empirical Results: poor condition number

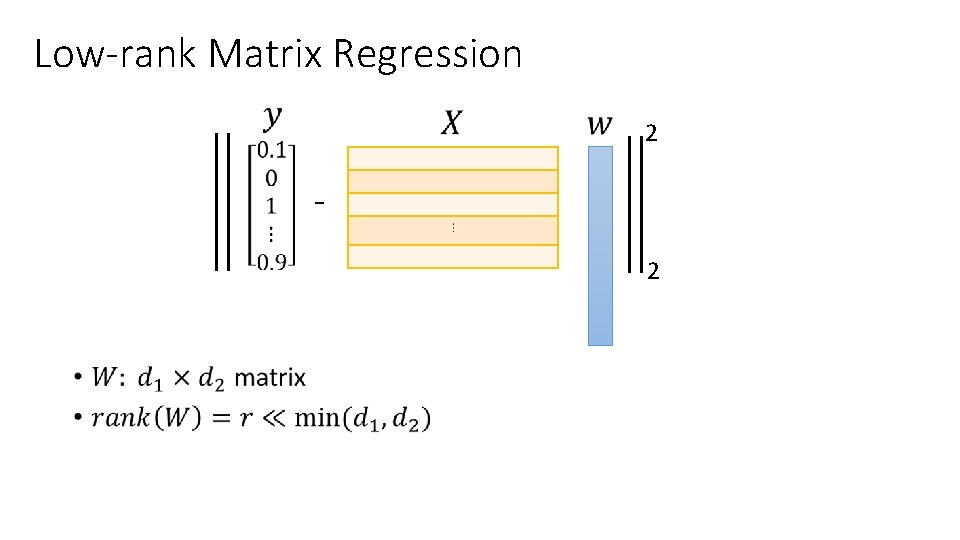
Low-rank Matrix Regression 2 2 •

Low-rank Matrix Regression •
![Statistical Guarantees J Tewari Kar 2014 Statistical Guarantees • [J. , Tewari, Kar’ 2014]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-28.jpg)
Statistical Guarantees • [J. , Tewari, Kar’ 2014]

Low-rank Matrix Completion • Special case of low-rank matrix regression • However, assumptions required by the regression analysis not satisfied
![Guarantees J Netrapalli 2015 Guarantees • [J. , Netrapalli’ 2015]](https://slidetodoc.com/presentation_image_h/2bd70e36b85c5c0a5db11eff7caae326/image-30.jpg)
Guarantees • [J. , Netrapalli’ 2015]

Tale of two Lemmas •

Empirical Results Matrix Regression Hard Thresholding Trace-norm Number of data points (n)

Summary •

Future Work • Generalized theory for such provable non-convex optimization • Performance analysis on different models • Empirical comparisons on “real-world” datasets

Questions?
 Linear regression vs multiple regression
Linear regression vs multiple regression Logistic regression vs linear regression
Logistic regression vs linear regression Logistic regression vs linear regression
Logistic regression vs linear regression Multiple regression formula
Multiple regression formula Prateek jain
Prateek jain Prateek bhopale
Prateek bhopale Prateek singh game
Prateek singh game Prateek mittal
Prateek mittal Prateek jain msr
Prateek jain msr Basic global thresholding
Basic global thresholding Dam construction in digital image processing
Dam construction in digital image processing Threshold image matlab
Threshold image matlab Thresholding in digital image processing
Thresholding in digital image processing Thresholding
Thresholding Optimum global thresholding using otsu's method
Optimum global thresholding using otsu's method Singular value thresholding
Singular value thresholding Gray level thresholding
Gray level thresholding What makes water hard
What makes water hard Work hard. have fun. make history
Work hard. have fun. make history Hard times hard drive
Hard times hard drive What is a regressor in linear regression
What is a regressor in linear regression Multiple linear regression variance
Multiple linear regression variance Anova
Anova Least square method
Least square method Aleksandar prokopec
Aleksandar prokopec Linear regression andrew ng
Linear regression andrew ng Y bar in regression
Y bar in regression Coefficient of determination interpretation
Coefficient of determination interpretation Chapter 7 linear regression
Chapter 7 linear regression Linear regression loss function
Linear regression loss function Linear regression formula
Linear regression formula Ap statistics linear regression
Ap statistics linear regression Linear least squares regression
Linear least squares regression Cost function machine learning
Cost function machine learning Disadvantages of linear regression
Disadvantages of linear regression Knn linear regression
Knn linear regression