Iterative Channel Estimation for Turbo Codes over Fading

Iterative Channel Estimation for Turbo Codes over Fading Channels Matthew C. Valenti Assistant Professor Dept. of Comp. Sci. & Elect. Eng. West Virginia University Morgantown, WV 26506 -6109 mvalenti@wvu. edu This work supported by ONR award N 00014 -00 -1 -0655

Overview n Turbo codes. n n Methods for detecting turbo codes over fading channels. n n n Practical problems over fading channels. DPSK-based Pilot-based Improved pilot-symbol techniques n Iterative channel estimation and decoding

Turbo Codes n Features: n Parallel Code Concatenation n Nonuniform interleaving Recursive systematic encoding n n n Can also use a serial concatenation Usually RSC convolutional codes are used. Can use block codes. Iterative decoding algorithm. n n Optimal approaches: BCJR/MAP, SISO, log-MAP Suboptimal approaches: max-log-MAP, SOVA
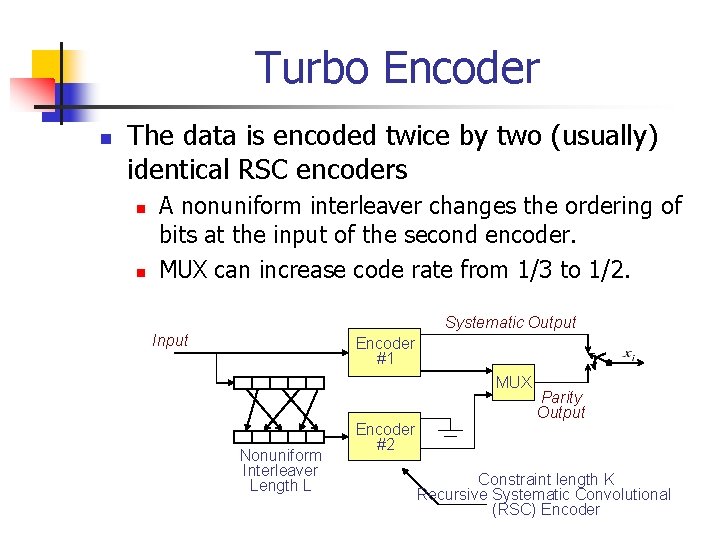
Turbo Encoder n The data is encoded twice by two (usually) identical RSC encoders n n A nonuniform interleaver changes the ordering of bits at the input of the second encoder. MUX can increase code rate from 1/3 to 1/2. Systematic Output Input Encoder #1 MUX Nonuniform Interleaver Length L Encoder #2 Parity Output Constraint length K Recursive Systematic Convolutional (RSC) Encoder
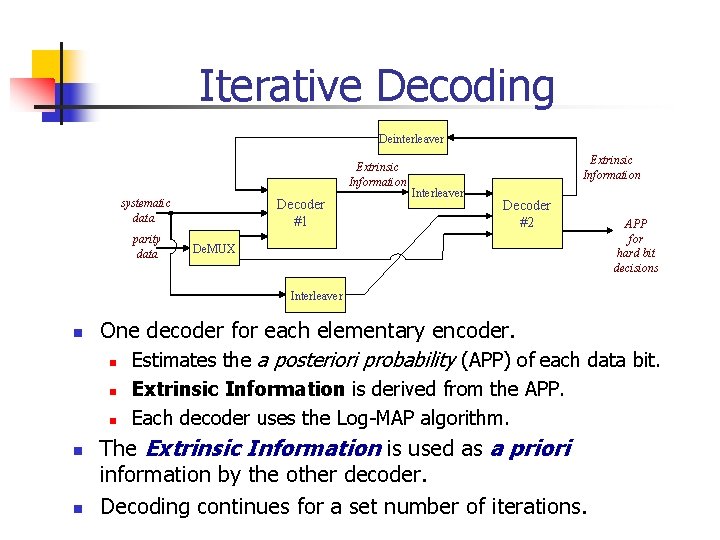
Iterative Decoding Deinterleaver Extrinsic Information systematic data parity data Decoder #1 Extrinsic Information Interleaver Decoder #2 De. MUX APP for hard bit decisions Interleaver n One decoder for each elementary encoder. n Estimates the a posteriori probability (APP) of each data bit. n n Extrinsic Information is derived from the APP. Each decoder uses the Log-MAP algorithm. The Extrinsic Information is used as a priori information by the other decoder. Decoding continues for a set number of iterations.

Turbo Codes for Fading Channels n Many channels of interest can be modeled as a frequency-flat fading channel. n n n Because of the time-varying nature of the channel, it is necessary to estimate and track the channel. n n Fading: channel is time-varying Flat: all frequencies experience same attenuation Channel estimation is difficult for turbo codes because they operate at low SNR. The goal of this study is to develop channel estimation techniques that take into account the iterative nature of the decoder.
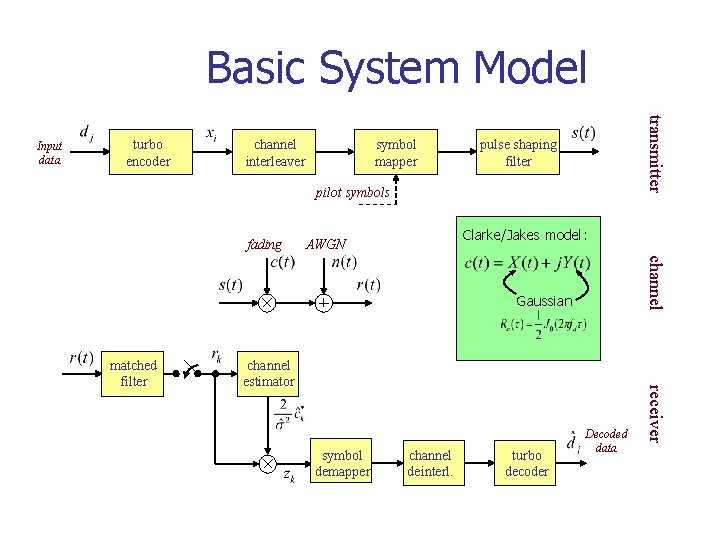
Basic System Model turbo encoder channel interleaver symbol mapper transmitter Input data pulse shaping filter pilot symbols fading Clarke/Jakes model: AWGN channel Gaussian channel estimator symbol demapper channel deinterl. turbo decoder Decoded data receiver matched filter

Channel Estimation for Turbo Codes n The turbo decoding algorithm requires accurate estimates of channel parameters. n Branch metric: n Noise variance: n n n Fading amplitude: Phase: (required for coherent detection) Because turbo codes operate at low SNR, conventional methods for channel estimation often fail. n Therefore channel estimation and tracking is a critical issue with turbo codes.

The Phase Ambiguity Problem n n If the receiver is operating at low SNR, accurate estimates of the phase k will not be available. A proactive solution to the phase ambiguity problem is required. n Use DPSK. n n n Differential detection Multiple-symbol differential detection. Use a pilot. n n Pilot tone. Pilot symbol.

DPSK for Turbo Codes n When differential detection is used with DSPK, a severe performance loss occurs. n n n ~ 4. 5 d. B loss for turbo codes in Rayleigh fading n Noncoherent combining loss. Not a viable option. However, multiple-symbol differential detection can be used to approach coherent performance. n P. Hoeher and J. Lodge n n “Turbo-DPSK” Serial code concatenation n n Convolutional outer code Accumulator inner code Per-survivor processing and linear prediction Globecom 98. & Trans. Comm. 99

Coherent Detection using Pilot Symbols n Coherent detection over Rayleigh fading channels requires a pilot. n Pilot tone n TTIB: Transparent Tone in Band n n Pilot symbols n PSAM: Pilot Symbol Assisted Modulation n n 1984: Mc. Geehan and Bateman 1987: Lodge and Moher; 1991: Cavers PSAM has been shown to be more power efficient than TTIB for turbo codes. n L. -D. Jeng, Y. -T. Su, and J. -T. Chiang, “Performance of turbo codes in multipath fading channels, ” VTC 98.
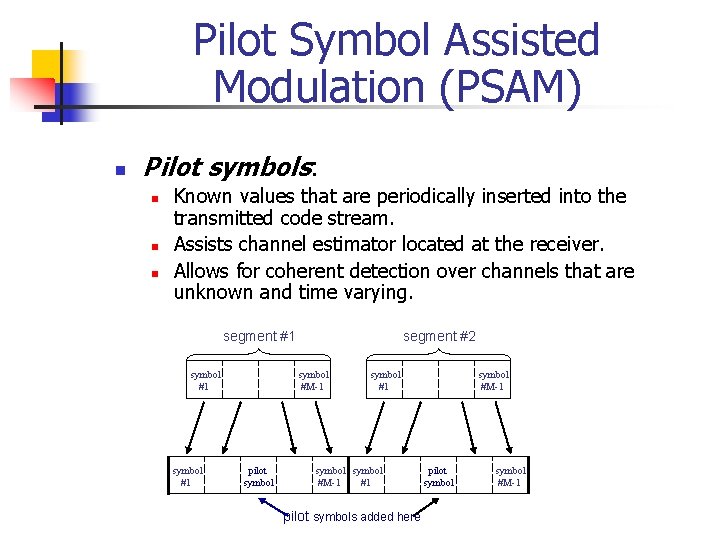
Pilot Symbol Assisted Modulation (PSAM) n Pilot symbols: n n n Known values that are periodically inserted into the transmitted code stream. Assists channel estimator located at the receiver. Allows for coherent detection over channels that are unknown and time varying. segment #1 symbol #1 segment #2 symbol #M-1 pilot symbol #1 symbol #M-1 #1 pilot symbols added here symbol #M-1 pilot symbol #M-1
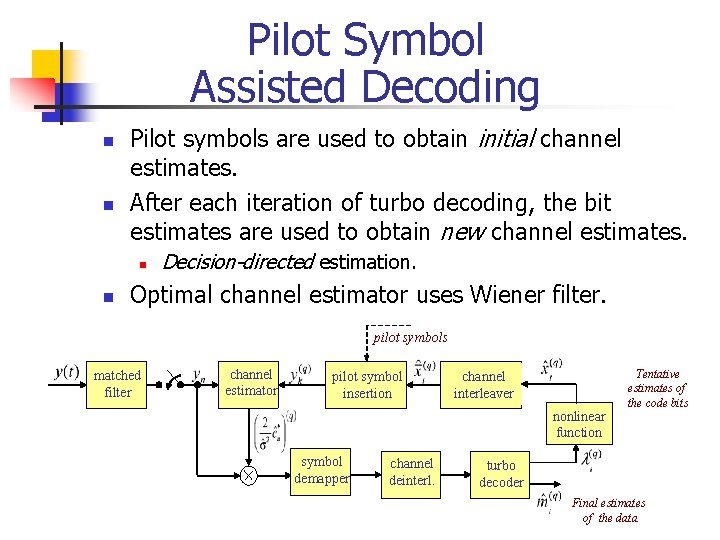
Pilot Symbol Assisted Decoding n n Pilot symbols are used to obtain initial channel estimates. After each iteration of turbo decoding, the bit estimates are used to obtain new channel estimates. n n Decision-directed estimation. Optimal channel estimator uses Wiener filter. pilot symbols matched filter channel estimator pilot symbol insertion channel interleaver nonlinear function symbol demapper channel deinterl. Tentative estimates of the code bits turbo decoder Final estimates of the data

Hard vs. Soft-Decision Feedback n Hard-decision feedback n Valenti & Woerner n n 1998 Electronics Letters, 1999 MILCOM Soft-decision feedback n Sandell, Luschi, Strauch, Yan n 1998 Globecom (for convolutional coding & equalization)
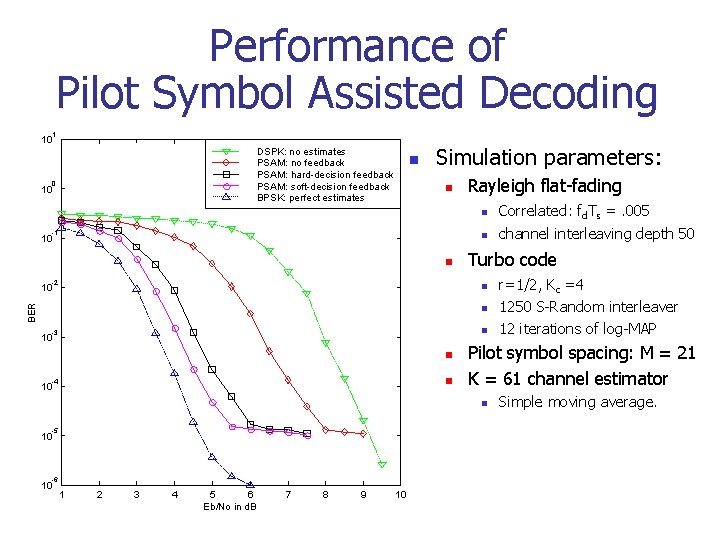
Performance of Pilot Symbol Assisted Decoding 1 10 DSPK: no estimates PSAM: no feedback PSAM: hard-decision feedback PSAM: soft-decision feedback BPSK: perfect estimates 0 10 n Simulation parameters: n -1 10 n -2 10 Rayleigh flat-fading n Correlated: fd. Ts =. 005 n channel interleaving depth 50 Turbo code BER n n n -3 10 n n -4 10 Pilot symbol spacing: M = 21 K = 61 channel estimator n -5 10 -6 10 1 2 3 4 5 6 Eb/No in d. B 7 8 9 10 r=1/2, Kc =4 1250 S-Random interleaver 12 iterations of log-MAP Simple moving average.
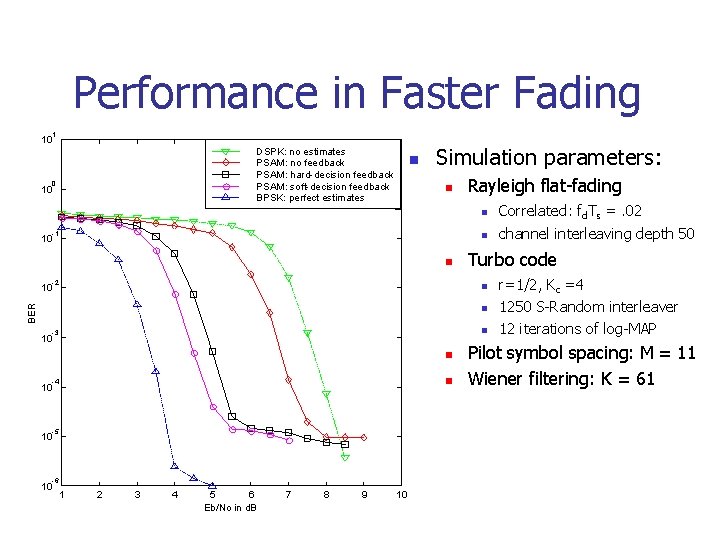
Performance in Faster Fading 1 10 DSPK: no estimates PSAM: no feedback PSAM: hard-decision feedback PSAM: soft-decision feedback BPSK: perfect estimates 0 10 n Simulation parameters: n -1 10 n -2 10 Rayleigh flat-fading n Correlated: fd. Ts =. 02 n channel interleaving depth 50 Turbo code BER n n n -3 10 n n -4 10 -5 10 -6 10 1 2 3 4 5 6 Eb/No in d. B 7 8 9 10 r=1/2, Kc =4 1250 S-Random interleaver 12 iterations of log-MAP Pilot symbol spacing: M = 11 Wiener filtering: K = 61

Performance Factors for Pilot Symbol Assisted Decoding n n Performance is more sensitive to errors in estimates of the fading process than estimates in noise variance. Pilot symbol spacing n n n Type of channel estimation filter n n n Want symbols close enough to track the channel. However, using pilot symbols reduces the energy available for the traffic bits. Wiener filter provides optimal solution. However, for small fd, a moving average is acceptable. Size of channel estimation filter n Window size of filter should contain about 4 pilot symbols.
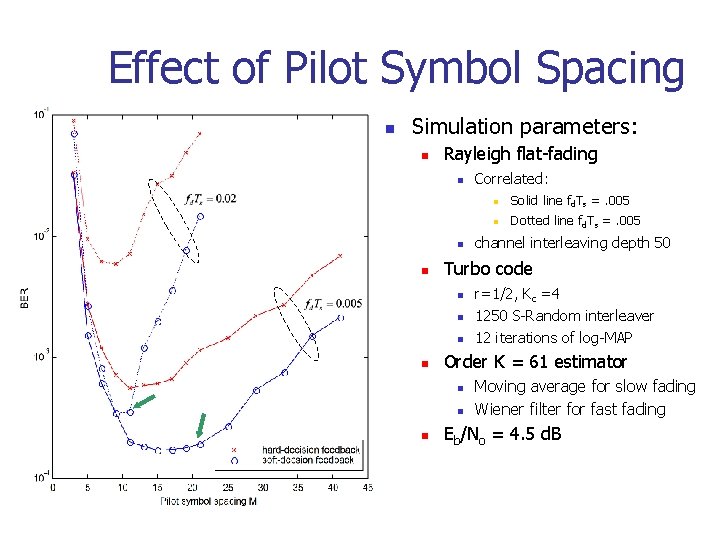
Effect of Pilot Symbol Spacing n Simulation parameters: n Rayleigh flat-fading n n n Solid line fd. Ts =. 005 n Dotted line fd. Ts =. 005 channel interleaving depth 50 r=1/2, Kc =4 1250 S-Random interleaver 12 iterations of log-MAP Order K = 61 estimator n n Turbo code n n Correlated: Moving average for slow fading Wiener filter for fast fading Eb/No = 4. 5 d. B

Future Work n Compare coherent PSAM technique with multiple-symbol DSPK technique. n n Incorporate adaptability n n In terms of performance and complexity. Adaptive estimation filters (Kalman). Adaptive pilot-symbol spacing. Extend the results to higher order modulation and trellis coded modulation. Extend the results to the problems of symboltiming estimation and frame synchronization.

Conclusions n Pilot symbol assisted decoding can be used to achieve nearly coherent detection/decoding of turbo codes. n n n Iterative estimation/decoding improves performance. Good performance even with just hard-decision feedback. Iterative estimation can also be used for other types of codes.
- Slides: 20