Iterative Algorithms Loop Invariants Steps in an Iterative
















































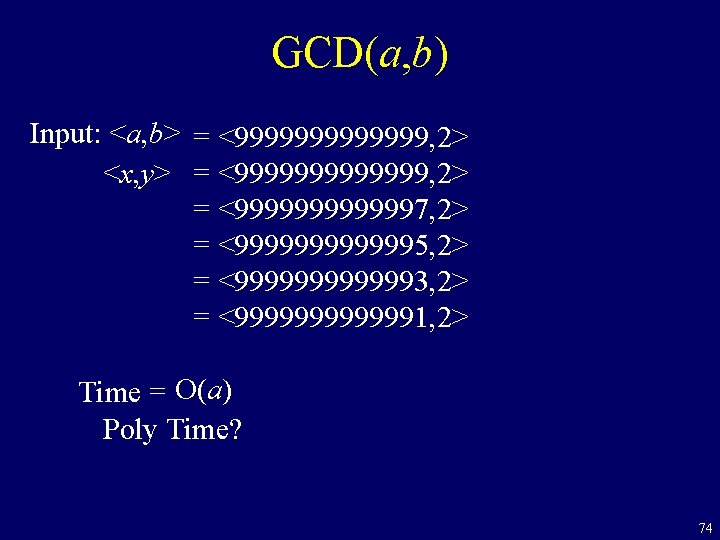








![Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work](https://slidetodoc.com/presentation_image_h2/d558855efd06a83e96e61a89715e5f4b/image-86.jpg)
![Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Time: • Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Time: •](https://slidetodoc.com/presentation_image_h2/d558855efd06a83e96e61a89715e5f4b/image-87.jpg)
![Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work](https://slidetodoc.com/presentation_image_h2/d558855efd06a83e96e61a89715e5f4b/image-88.jpg)







- Slides: 105

Iterative Algorithms & Loop Invariants Steps in an Iterative Algorithm Code from LI Fairy God Mother (Lake) More of Input (Insertion and DFA) More of Output (Selection & Blocks) Narrowing the search space Shrinking Instance (GCD) (Running Time) Jeff's result Lecture 1 Jeff Edmonds York University COSC 31011

A Sequencevs of Actions A Sequence of Assertions Max( a, b, c ) “pre. Cond: Input has 3 numbers. ” m=a “assert: m is max in {a}” if( b>m ) m=b endif “assert: m is max in {a, b}” if( c>m ) m=c endif “assert: m is max in {a, b, c}” return(m) “post. Cond: return max in {a, b, c}” It is helpful to have different ways of looking at it. 2

Purpose of Assertions Useful for – thinking about algorithms – developing – describing – proving correctness 3

Definition of Assertions An assertion is a statement about the current state of the data structure that is either true or false. eg. the amount in your bank account is not negative. 4

Definition of Assertions It is made at some particular point during the execution of an algorithm. It should be true independent of the path followed through the code and independent of the input. If it is false, then something has gone wrong in the logic of the algorithm. 5

Definition of Assertions An assertion is not a task for the algorithm to perform. It is only a comment that is added for the benefit of the reader. 6

Definition of Assertions • The current state of the computation – Everything that is true at a particular instant in time. – Imagine flying in from Mars, what do you need to know about the present to be able to continue. – It does not say anything about the past, i. e. how the computation got here. – Eg <x=8, y=3, current line of code = line 84> 7

Definition of Assertions • The current state of the computation • An assertion, A – is a function • that takes as input the current state • and that outputs True or False – Eg A = “x is odd” • A(<x=5, y=3, line 84> ) = True Computation is on the path • A(<x=8, y=3, line 84> ) = False Something has gone wrong! 8

Algorithm Termination You need to define some Measure of progress to prove that your algorithm eventually terminates. • An Measure of Progress, M – is a function • that takes as input the current state • and that outputs a real number – Eg Measure = “value of y” • M(<x=5, y=3, line 84> ) = 3 – We must prove that this number goes down (up) each iteration. 9

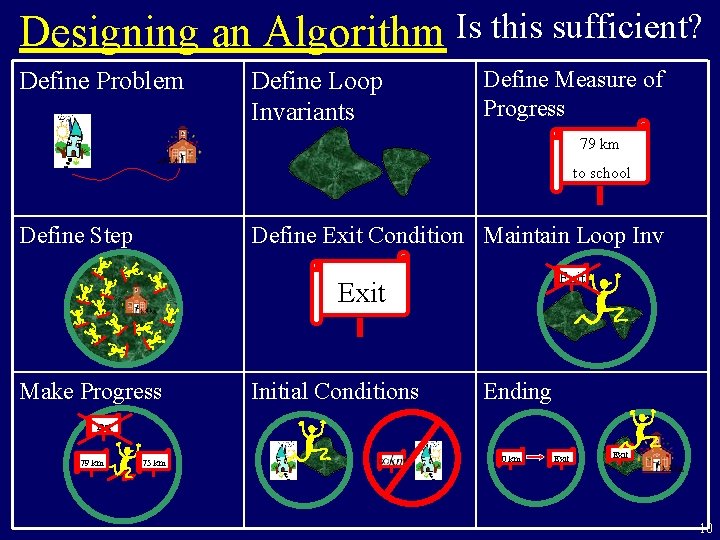
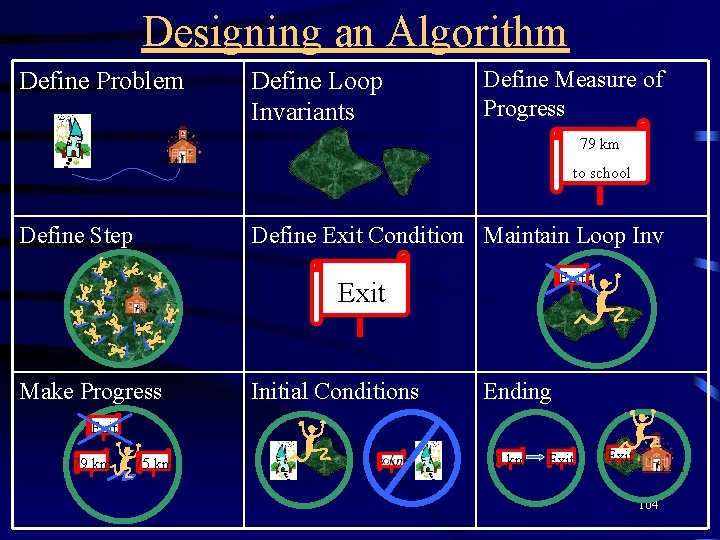
Designing an Algorithm Is this sufficient? Define Problem Define Loop Invariants Define Measure of Progress 79 km to school Define Step Define Exit Condition Maintain Loop Inv Exit Make Progress Initial Conditions Ending Exit 79 km 75 km 0 km Exit 10

Explaining Insertion Sort We maintain a subset of elements sorted within a list. The remaining elements are off to the side somewhere. Initially, think of the first element in the array as a sorted list of length one. One at a time, we take one of the elements that is off to the side and we insert it into the sorted list where it belongs. This gives a sorted list that is one element longer than it was before. When the last element has been inserted, the array is completely sorted. 88 52 14 31 25 98 30 23 62 79 14, 23, 25, 30, 31, 52, 62, 79, 88, 98 11

Partial Correctness Establishing Loop Invariant <pre. Cond> code. A <loop-invariant> Maintaining Loop Invariant Exit <loop-invariant> ¬<exit Cond> code. B <loop-invariant> Clean up loose ends <loop-invariant> <post. Cond> <exit Cond> Exit code. C Proves that IF the program terminates then it works <Pre. Cond> & <code> <Post. Cond> 12

Consider an Algorithm Exit 79 km 75 km 0 km Exit 13

Loop Invariant Maintained Exit 14

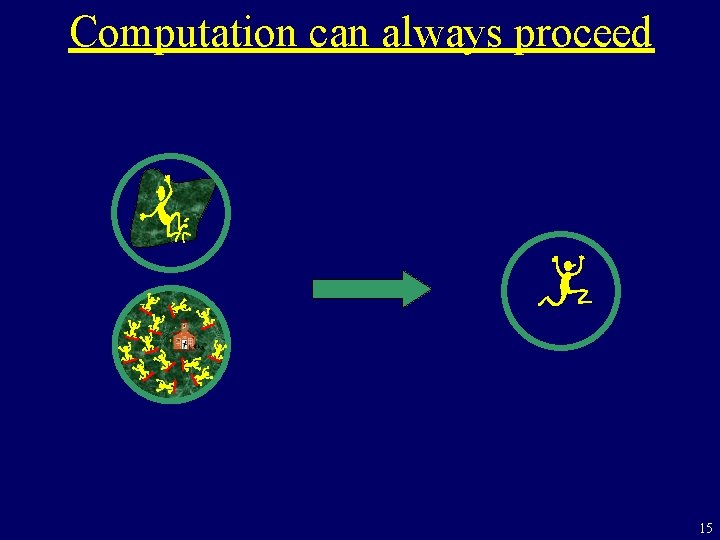
Computation can always proceed 15

Computation always makes progress 79 km 75 km Exit 79 km 75 km 16

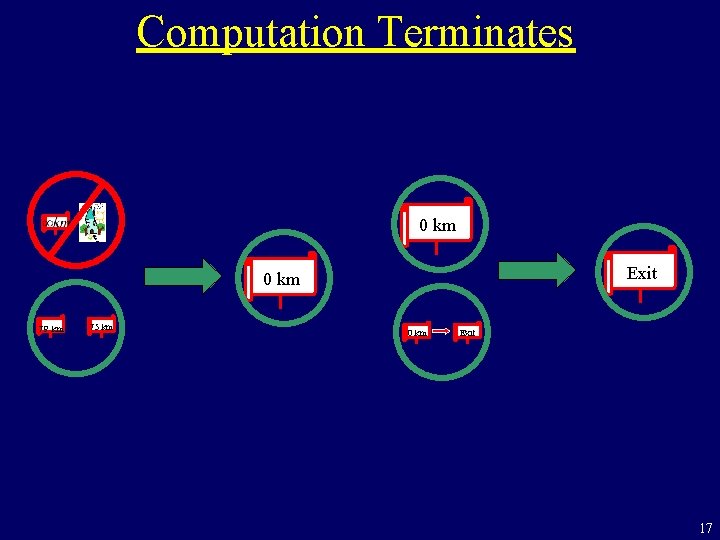
Computation Terminates 0 km Exit 0 km 79 km 75 km 0 km Exit 17

Computation Terminates Exit 18

Consider an Algorithm Exit 79 km 75 km 0 km Exit This is sufficient! 19

Designing an Algorithm Define Problem Define Loop Invariants Define Measure of Progress 79 km Define Step Define Exit Condition Maintain Loop Inv Exit Make Progress Initial Conditions Ending Exit 79 km 75 km 0 km Exit 20

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • What is the loop invariant? • Each iteration add in a new object. Action not picture If you fight me, I will fail you 21

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • What is the loop invariant? • What do you want to be true in the middle of the computation? • To have a partial sum: s = 12 + 22 + 32 + … + i 2 (and 1 ≤ i ≤ I) 22

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (0 ≤ i ≤ I) 79 km Exit 79 km 75 km Exit • Measure of Progress • i = # of objects added. • Step to make progress • i = i+1 • Exit Condition • i=I 23

Code from LI In order to make progress, we may head in one direction. Exit 79 km 75 km • Step to make progress • i = i+1 24

Code from LI In order to make progress, we may head in one direction. Exit 79 km 75 km • Step to make progress • i = i+1 25

Code from LI Exit In order to maintain the loop invariant, we must adjust to come back to the path. 26

Code from LI This may be how we determine the step in then next iteration. 27

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Partial Step: i = i+1 Maintaining Loop Invariant Exit <loop-invariantt> ¬<exit Cond> code. B <loop-invariantt+1> Let it and st be the values of i and s at the beginning of the iteration and let it+1 and st+1 be their after going around again. 28

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Partial Step: i = i+1 Use the fact that you <loop-invariantt> already have the LI true and take a small step. ¬<exit Cond> code. B: Make the loop Invariant true!!! Solve the entire algorithm!!! Panic!! next <loop-invariantt+1> 29

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Partial Step: i = i+1 (code. B in loop) st = 1 2 + 2 2 + 3 2 + … + i t 2 <loop-invariantt> it < I ¬<exit Cond> it+1 = it + 1 (math) code. B: st+1 Write down LHS/RHS of what we must prove =12 + 22 + 32 + … + it+12 <loop-invariantt+1> 30

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Partial Step: i = i+1 st = 1 2 + 2 2 + 3 2 + … + i t 2 <loop-invariantt> it < I ¬<exit Cond> it+1 = it + 1 code. B: st+1 = st + it+12 =[12 + 22 + 32 + … + it 2 ]+ it+12 =12 + 22 + 32 + … + it+12 <loop-invariantt+1> 31

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Partial Step: i = i+1 s = s + i 2 i=i+1 it+1 = it + 1 st+1 = st + it+12 i=i+1 s = s + i 2 32

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Step: i = i+1, s = s + i 2 Clean up loose ends Exit <loop-invariant> <exit Cond> code. C <post. Cond> 33

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Step: i = i+1, s = s + i 2 <loop-invariant> <exit Cond> code. C: s = 12 + 22 + 32 + … + i 2 2 I i=I S=s S =12 + 22 + 32 + … + I 2 <post. Cond> 34

Code from LI • Precondition: The input is an integer I. • Postcondition: The output is S = 12 + 22 + 32 + … + I 2 • Loop Invariant: s = 12 + 22 + 32 + … + i 2 (1 ≤ i ≤ I) • Step: i = i+1, s = s + i 2 Establishing Loop Invariant <pre. Cond> code. A i=0 s=0 i 0 1 2 3 <loop-invariant> s 0 1 1+4=5 1+4+9=14 35

Designing an Algorithm Define Problem Define Loop Invariants Define Measure of Progress 79 km Define Step Define Exit Condition Maintain Loop Inv Exit Make Progress Initial Conditions Ending Exit 79 km 75 km 0 km Exit 36

Typical Types of Loop Invariants • • • Fairy God Mother More of the input More of the output Narowing the search space Shrinking Input Instance Data Structure (System) Invariant 37

Typical Types of Loop Invariants • Fairy God Mother – I have arrived from Mars, some amount of progress has been made already and my Fairy God Mother has set the state of the computation to be just what I want so that I feel as comfortable as I could be given the amount of progress that has been made. • • • More of the input More of the output Narowing the search space Shrinking Input Instance Data Structure (System) Invariant 38

Fairy God Mother Loop Invariants I run infinitely faster than the monster. so my only goal is to get to shore without him there. The only problem is that he runs 4 times faster than I swim. Me: Radius 1, speed 1, time 1. Him: Half circ. , speed 4, time = 3. 14/4 < 1 He wins. 39

Fairy God Mother Loop Invariants He runs back and forth to catch me. And I change my direction to avoid him. Can I get away? 40

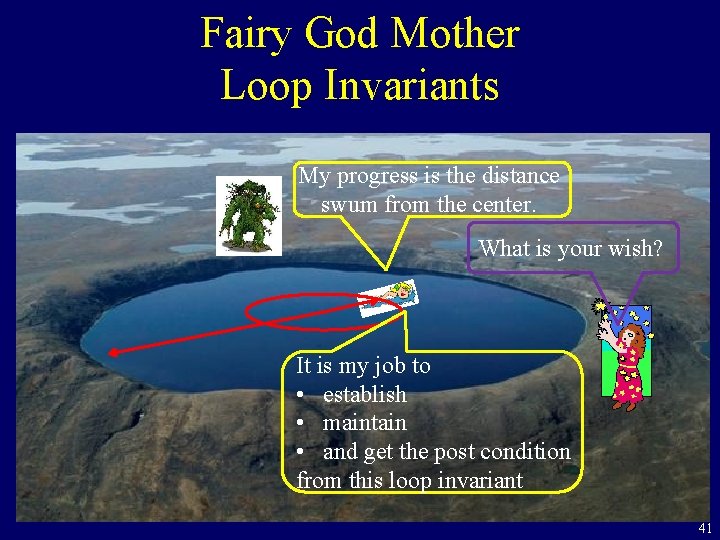
Fairy God Mother Loop Invariants My progress is the distance swum from the center. What is your wish? It is my job to • establish • maintain • and get the post condition from this loop invariant 41

Fairy God Mother Loop Invariants My goal now is not to excape or to make progress. My only goal is to extablish the loop invariant by. . ? Moving to the center. 42

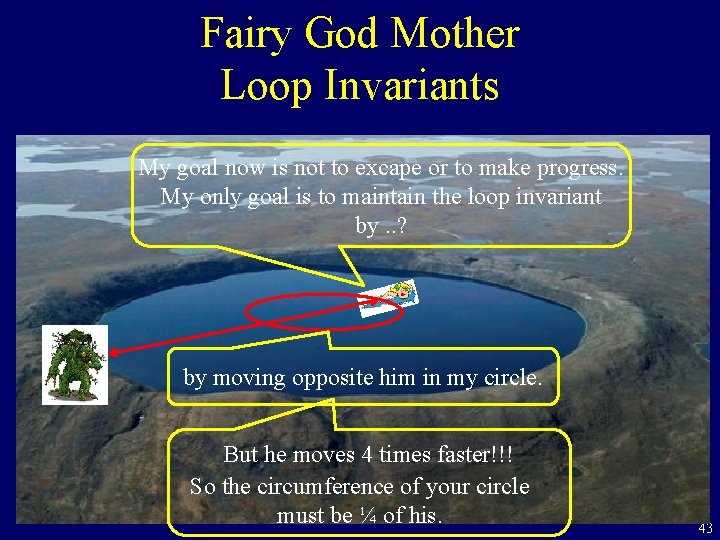
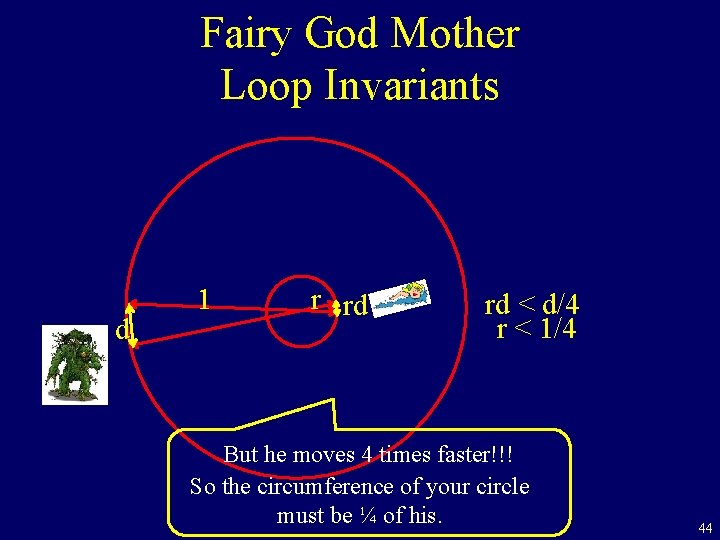
Fairy God Mother Loop Invariants My goal now is not to excape or to make progress. My only goal is to maintain the loop invariant by. . ? by moving opposite him in my circle. But he moves 4 times faster!!! So the circumference of your circle must be ¼ of his. 43

Fairy God Mother Loop Invariants d 1 r rd rd < d/4 r < 1/4 But he moves 4 times faster!!! So the circumference of your circle must be ¼ of his. 44

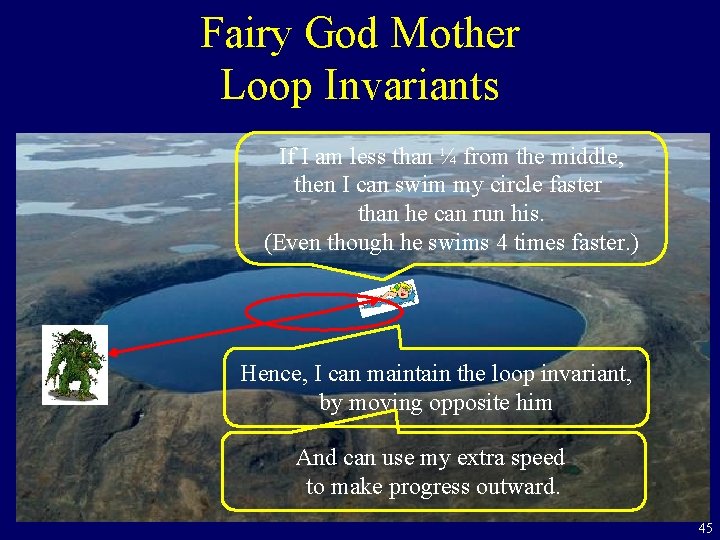
Fairy God Mother Loop Invariants If I am less than ¼ from the middle, then I can swim my circle faster than he can run his. (Even though he swims 4 times faster. ) Hence, I can maintain the loop invariant, by moving opposite him And can use my extra speed to make progress outward. 45

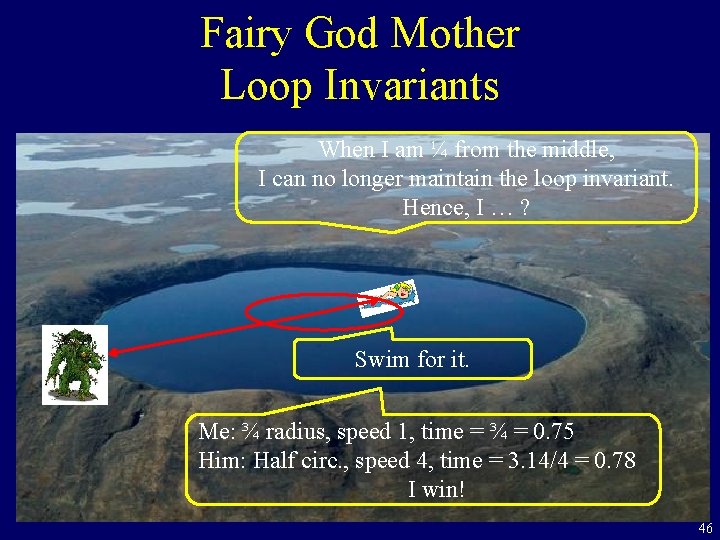
Fairy God Mother Loop Invariants When I am ¼ from the middle, I can no longer maintain the loop invariant. Hence, I … ? Swim for it. Me: ¾ radius, speed 1, time = ¾ = 0. 75 Him: Half circ. , speed 4, time = 3. 14/4 = 0. 78 I win! 46

Typical Types of Loop Invariants • • • Fairy God Mother More of the input More of the output Narowing the search space Shrinking Input Instance Data Structure (System) Invariant 47

More of the Input Loop Invariant The input consists of an array of objects Solution Extra We have read in the first i objects. We will pretend that this prefix is the entire input. We have a solution for this prefix plus some additional information 48

Loop Invariants and Deterministic Finite Automaton L = {a Î {0, 1}* | a has length at most three and the number of 1's is odd }. 49

More of the Input Loop Invariant The input consists of an array of objects Solution Extra We read in the i+1 st object. We will pretend that this larger prefix is the entire input. We extend the solution we have to one for this larger prefix. (plus some additional information) 50

More of the Input Loop Invariant The input consists of an array of objects Solution Exit 79 km 75 km Extra i to i+1 51

More of the Input Loop Invariant The input consists of an array of objects Solution Exit In the end, we have read in the entire input. The LI gives us that we have a solution for this entire input. 52

Insertion Sort The input consists of an array of integers 52, 23, 88, 31, 25, 30, 98, 62, 14, 79 23, 31, 52, 88 Solution We have read in the first i objects. We will pretend that this prefix is the entire input. We have a solution for this prefix 53

Insertion Sort The input consists of an array of integers 52, 23, 88, 31, 25, 30, 98, 62, 14, 79 23, 31, 52, 88 23, 25, 31, 52, 88 We read in the i+1 st object. We will pretend that this larger prefix is the entire input. We extend the solution we have to one for this larger prefix. 54

Typical Types of Loop Invariants • • • Fairy God Mother More of the input More of the output Narowing the search space Shrinking Input Instance Data Structure (System) Invariant 55

More of the Output Loop Invariant The output consists of an array of objects I have produced the first i objects. Produce the i+1 st output object. Exit 79 km 75 km i to i+1 Exit Done when output n objects. 56

Input: Selection Sort 52, 23, 88, 31, 25, 30, 98, 62, 14, 79 The output consists of an array of integers 14, 23, 25, 30, 31, 52, 62, 79, 88, 98 I have produced the first i objects. Produce the i+1 st output object. Exit Done when output n objects. 57

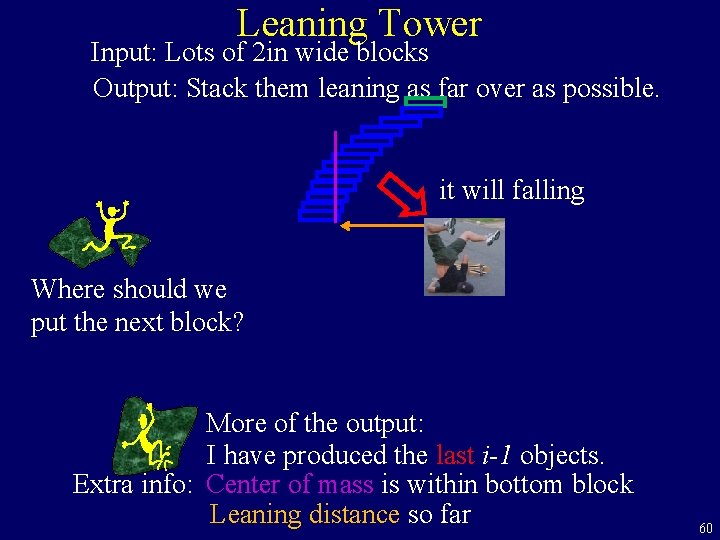
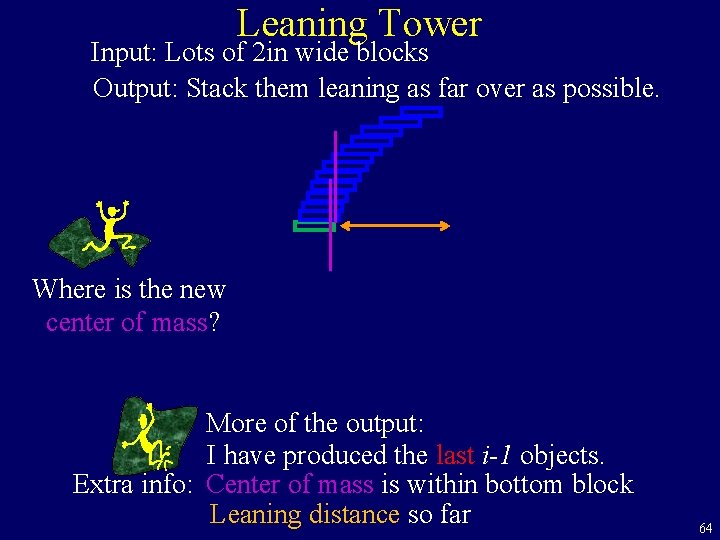
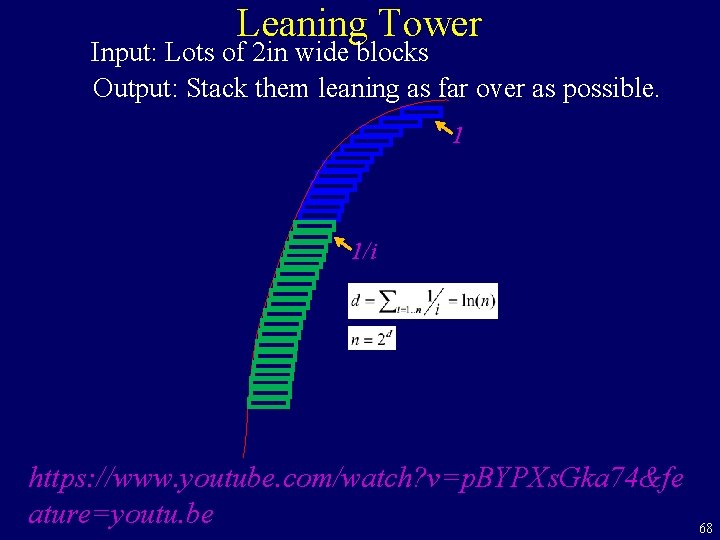
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. With out falling How far over can you shift it go over? More of the output? 58

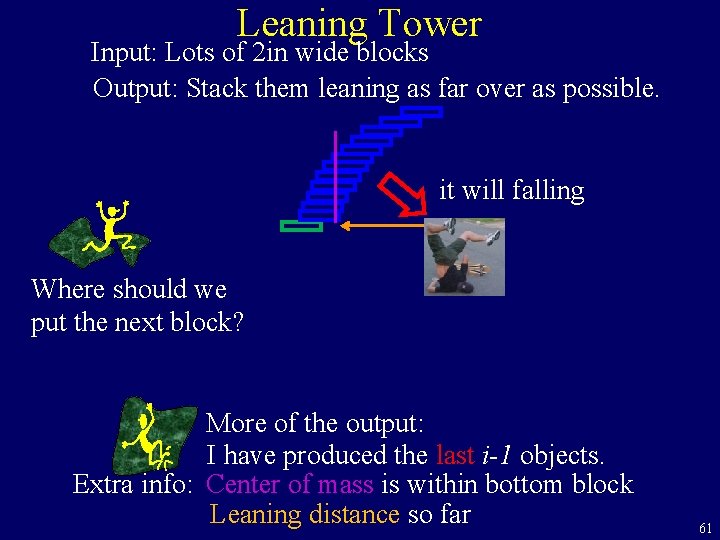
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. But if I keep adding blocks it will falling Is this a proof that it is not possible? Try again More of the output: I have produced the first i-1 objects. 59

Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. it will falling Where should we put the next block? More of the output: I have produced the last i-1 objects. Extra info: Center of mass is within bottom block Leaning distance so far 60

Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. it will falling Where should we put the next block? More of the output: I have produced the last i-1 objects. Extra info: Center of mass is within bottom block Leaning distance so far 61

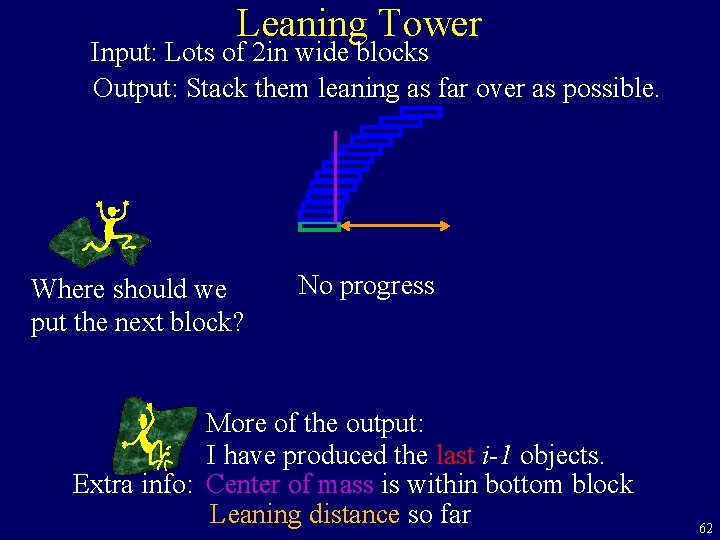
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. Where should we put the next block? No progress More of the output: I have produced the last i-1 objects. Extra info: Center of mass is within bottom block Leaning distance so far 62

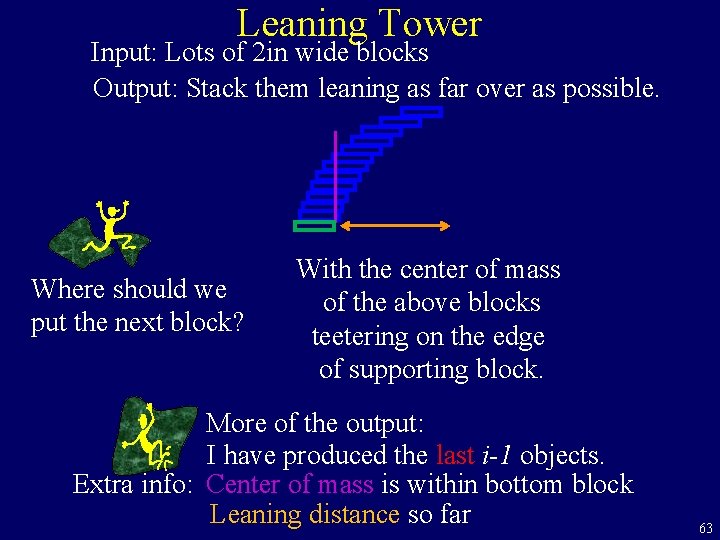
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. Where should we put the next block? With the center of mass of the above blocks teetering on the edge of supporting block. More of the output: I have produced the last i-1 objects. Extra info: Center of mass is within bottom block Leaning distance so far 63

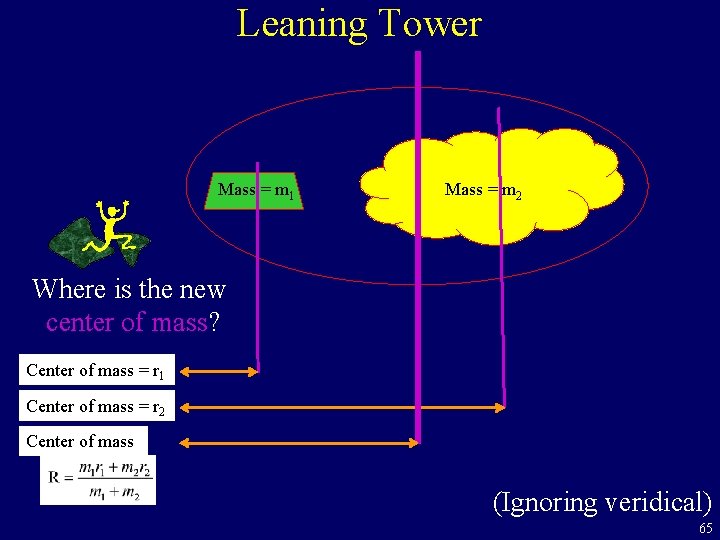
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. Where is the new center of mass? More of the output: I have produced the last i-1 objects. Extra info: Center of mass is within bottom block Leaning distance so far 64

Leaning Tower Mass = m 1 Mass = m 2 Where is the new center of mass? Center of mass = r 1 Center of mass = r 2 Center of mass (Ignoring veridical) 65

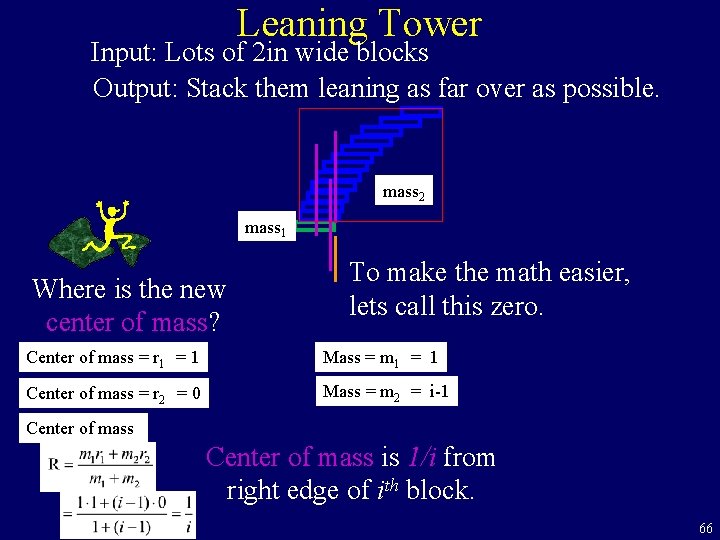
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. mass 2 mass 1 Where is the new center of mass? To make the math easier, lets call this zero. Center of mass = r 1 = 1 Mass = m 1 = 1 Center of mass = r 2 = 0 Mass = m 2 = i-1 Center of mass is 1/i from right edge of ith block. 66

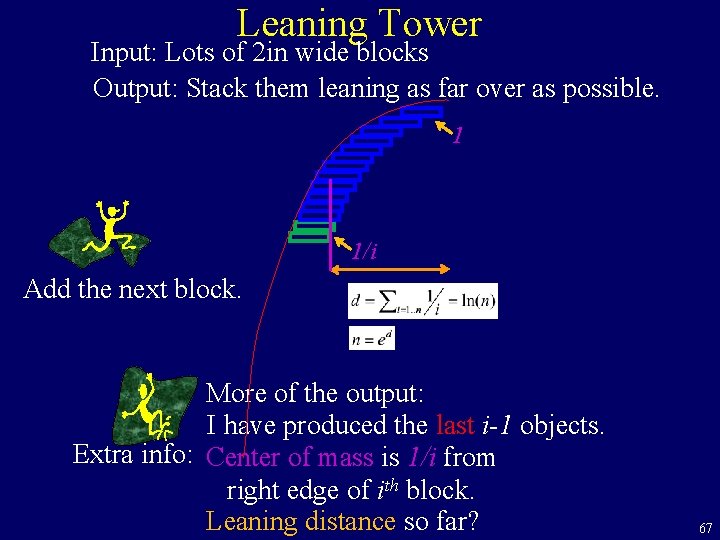
Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. 1 1/i Add the next block. More of the output: I have produced the last i-1 objects. Extra info: Center of mass is 1/i from right edge of ith block. Leaning distance so far? 67

Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. 1 1/i https: //www. youtube. com/watch? v=p. BYPXs. Gka 74&fe ature=youtu. be 68

Leaning Tower Input: Lots of 2 in wide blocks Output: Stack them leaning as far over as possible. https: //www. youtube. com/watch? v=p. BYPXs. Gka 74&fe ature=youtu. be 69

Typical Types of Loop Invariants • • • Fairy God Mother More of the input More of the output Narowing the search space Shrinking Input Instance Data Structure (System) Invariant 70

Define Loop Invariant • Maintain a sub-list. • If the key is contained in the original list, then the key is contained in the sub-list. key 25 3 5 6 13 18 21 21 25 36 43 49 51 53 60 72 74 83 88 91 95 71

Typical Types of Loop Invariants • • • Fairy God Mother More of the input More of the output Narowing the search space Shrinking Input Instance An instance has been produced that is smaller than the actual instance and these two instances require the same output. Hence, it is su�cient for me to forget about the actual instance and simply give the output for the new smaller one. • Data Structure (System) Invariant 72

GCD(a, b) = <21, 9> Input: <a, b> Output: GCD(a, b) = 3 Maintain values <x, y> such that GCD(a, b) = GCD(x, y) GCD(a, b) = GCD(a-b, b) GCD(21, 9) = GCD(12, 9) = 3 Replace <x, y> with <x-y, y> GCD(a, b) = GCD(x, y) = GCD(x-y, y) = GCD(x’, y’) Exit 79 km 75 km smaller Running Time? 73
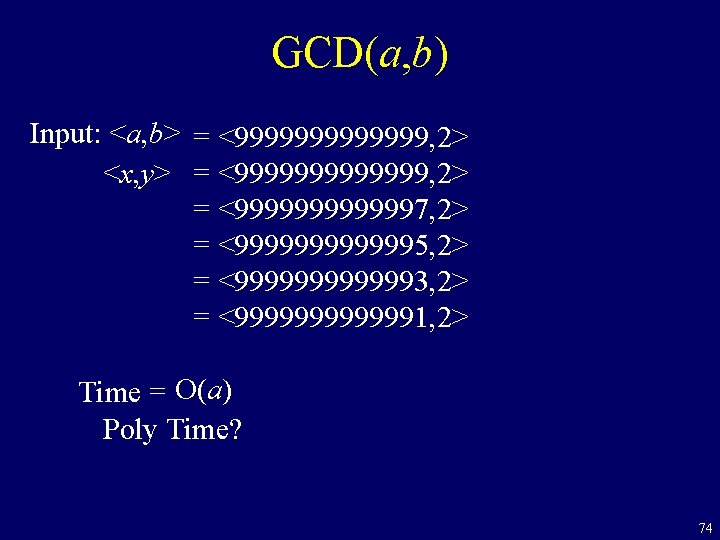
GCD(a, b) Input: <a, b> = <9999999, 2> <x, y> = <9999999, 2> = <9999997, 2> = <9999995, 2> = <9999993, 2> = <9999991, 2> Time = O(a) Poly Time? 74

Size of Input Instance 5 83920 1’’ 2’’ • • Size of paper # of bits # of digits Value - n = 2 in 2 - n = 17 bits - n = 5 digits - n = 83920 • • Intuitive Formal Reasonable Unreasonable # of bits = log 2(Value) Value = 2# of bits 75

GCD(a, b) Input: <a, b> = <9999999, 2> <x, y> = <9999999, 2> = <9999997, 2> = <9999995, 2> = <9999993, 2> = <9999991, 2> Time = O(a) = 2 O(n) Size = number of digits n = O(log(a)) 76

GCD(a, b) = <21, 9> Input: <a, b> Output: GCD(a, b) = 3 Maintain values <x, y> such that GCD(a, b) = GCD(x, y) GCD(a, b) GCD(21, 9) = GCD(a-b, b) = GCD(12, 9) = 3 = GCD(a mod b, b) = GCD(3, 9) Exit 79 km 75 km Much faster We want the first number the biggest 77

GCD(a, b) = <21, 9> Input: <a, b> Output: GCD(a, b) = 3 Maintain values <x, y> such that GCD(a, b) = GCD(x, y) GCD(a, b) GCD(21, 9) = GCD(a-b, b) = GCD(12, 9) = 3 = GCD(a mod b, b) = GCD(3, 9) = GCD(b, a mod b) = GCD(9, 3) 78

GCD(a, b) Input: <a, b> = <10000001, 9999999> <x, y> = <10000001, 9999999> = <9999999, 2> Little progress = <2, 1> Lots of progress = <1, 0> GCD(a, b) = GCD(x, y) = 1 Every two iterations: the value x decreases by at least a factor of 2. the size of x decreases by at least one bit Time = O(log(a)+log(b)) = O(n) Size = n = O(log(a)+log(b)) 79

GCD(a, b) 80

Two Graph Problems • Tournament • Euclidian Cycle 81

Mining for Empty Rectangles in Large Data Sets Jeff Edmonds Jarek Gryz Dongming Liang Renee Miller

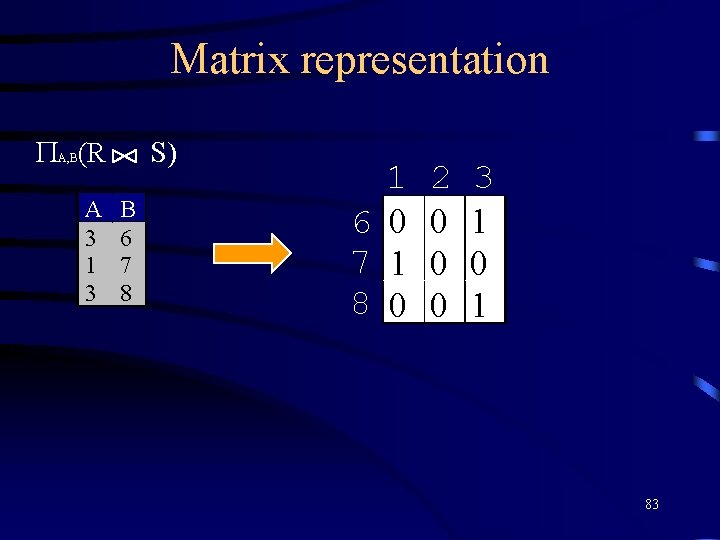
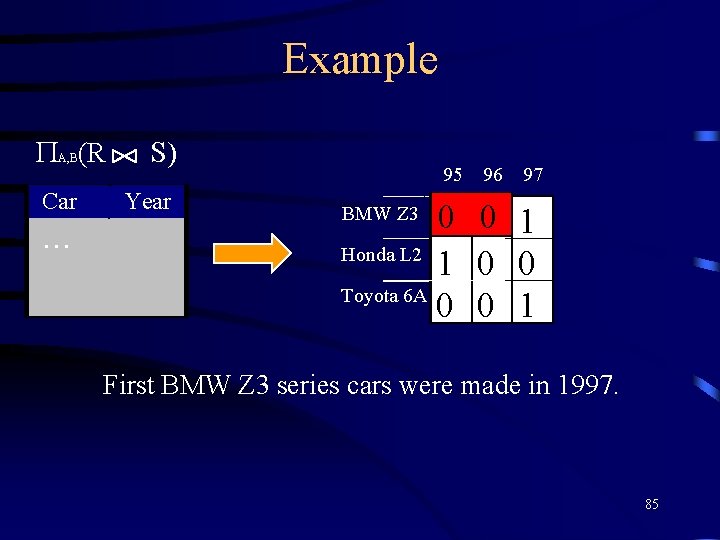
Matrix representation (R S) A, B A 3 1 3 B 6 7 8 1 6 0 7 1 8 0 2 0 0 0 3 1 0 1 83

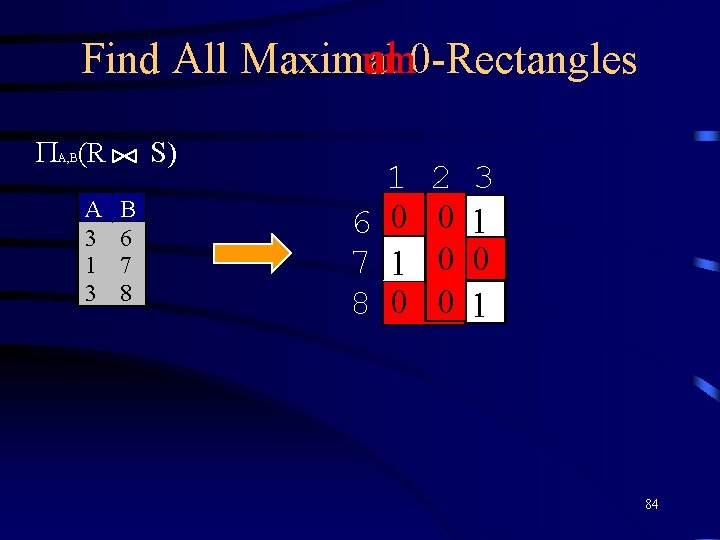
al 0 -Rectangles um Find All Maximal (R S) A, B A 3 1 3 B 6 7 8 1 6 0 7 1 8 0 2 00 00 00 3 1 0 1 84

Example (R A, B Car … S) Year 95 0 Honda L 2 1 Toyota 6 A 0 BMW Z 3 96 97 0 1 0 0 0 1 First BMW Z 3 series cars were made in 1997. 85
![Relation to Previous Work Namaad Hsu Lee Lui Ku Hsu Orlowski Our Work Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work](https://slidetodoc.com/presentation_image_h2/d558855efd06a83e96e61a89715e5f4b/image-86.jpg)
Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work Problem: Find all maximal empty rectangles • between points • within a 0 -1 matrix in real plane Purpose: • Machine Learning • Computational Geometry • Query Optimization # of maximal 0 -rectangles: • O( (# 1’s)2 ) • O( #0’s ) 86
![Relation to Previous Work Namaad Hsu Lee Lui Ku Hsu Orlowski Time Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Time: •](https://slidetodoc.com/presentation_image_h2/d558855efd06a83e96e61a89715e5f4b/image-87.jpg)
Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Time: • O( # 1’s log(#1’s) + # rectangles ) = O(|X||Y|) Space: • O(|X||Y|) Our Work • O( #0’s ) = O(|X||Y|) • O(min(|X|, |Y|)) • only two rows of matrix kept in memory 87
![Relation to Previous Work Namaad Hsu Lee Lui Ku Hsu Orlowski Our Work Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work](https://slidetodoc.com/presentation_image_h2/d558855efd06a83e96e61a89715e5f4b/image-88.jpg)
Relation to Previous Work [Namaad, Hsu, Lee] [Lui, Ku, Hsu] & [Orlowski] Our Work Practical Implementation: • Intensive random Requires a single scan memory access of the sorted data Scalable: • Scales Badly Practical? • Scales well wrt • # of tuples in join • # of maximal rectangles • # of values |X| & |Y| • IBM paid us $25, 000 88 to patent it!

Structure of Algorithm loop y = 1. . |Y| loop x = 1. . |X| • Output all maximal 0 -rectangles with <x, y> as bottom-right corner • Maintain the loop invariant 1 YX 1 1 0 • 0 1 <x, y> * 1 1 Timing O(1) amortized time per <x, y> 89

Designing an Algorithm Define Problem Define Loop Invariants Define Measure of Progress 79 km to school Define Step Define Exit Condition Maintain Loop Inv Exit Make Progress Initial Conditions Ending Exit 79 km 75 km 0 km Exit 90

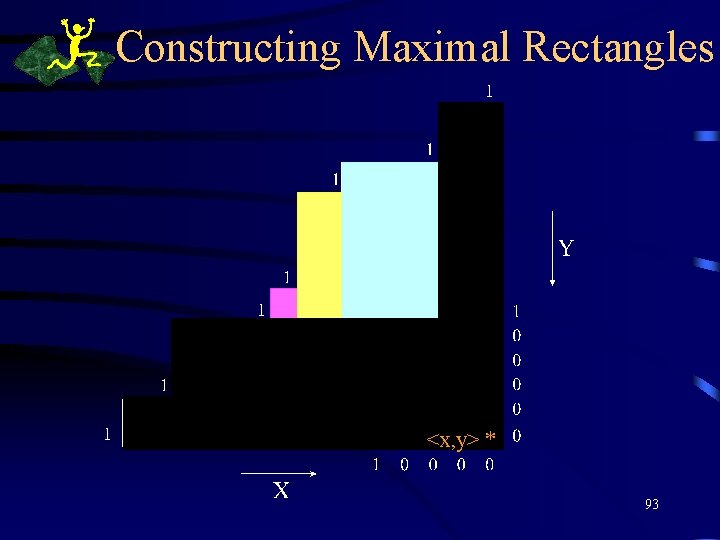
Define the Loop Invariant • We have read the matrix up to <x, y> and cannot reread the matrix. • We must output all maximal 0 -rectangles with <x, y> as bottom-right corner • What must we remember? 1 YX 1 1 0 • 0 1 <x, y> * 1 1 91

1 ( xr , yr ) 1 ( x 5 , y 5) Stack of steps ( x 4 , y 4) 1 step ( x 3 , y 3) ( x 2 , y 2) ( x 1 , y 1) 1 Y 0 1 y 1 1 <x, y> * 1 X x* 0 0 0 1 * 0 0 0 92

Constructing Maximal Rectangles <x, y> * 93

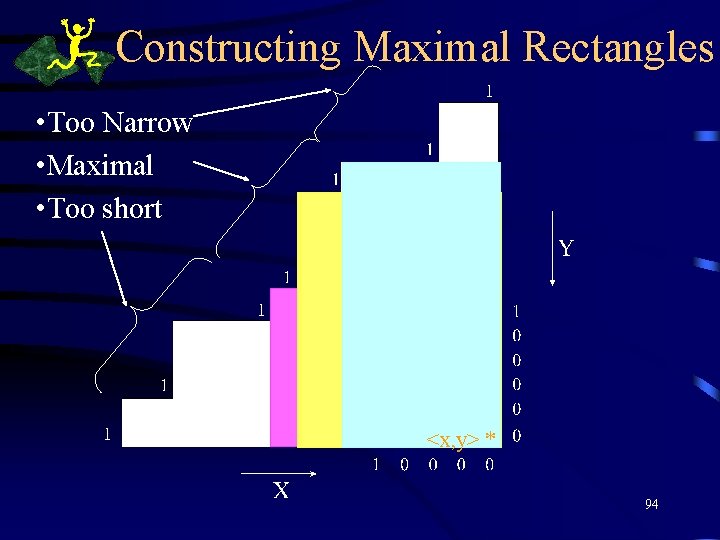
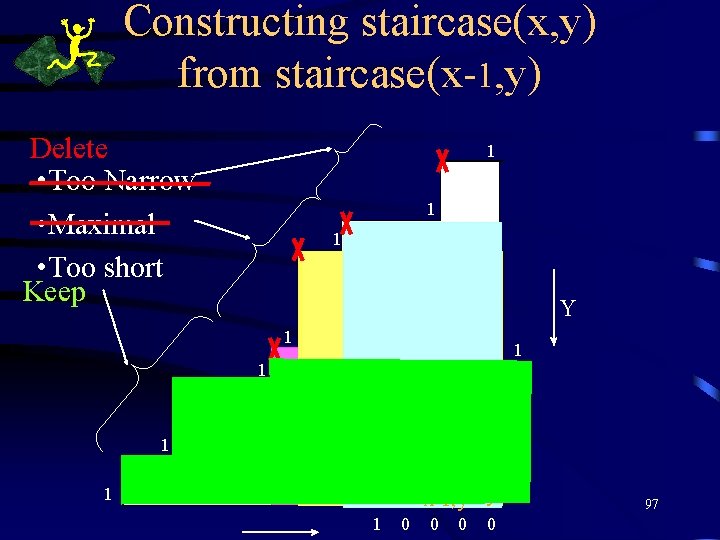
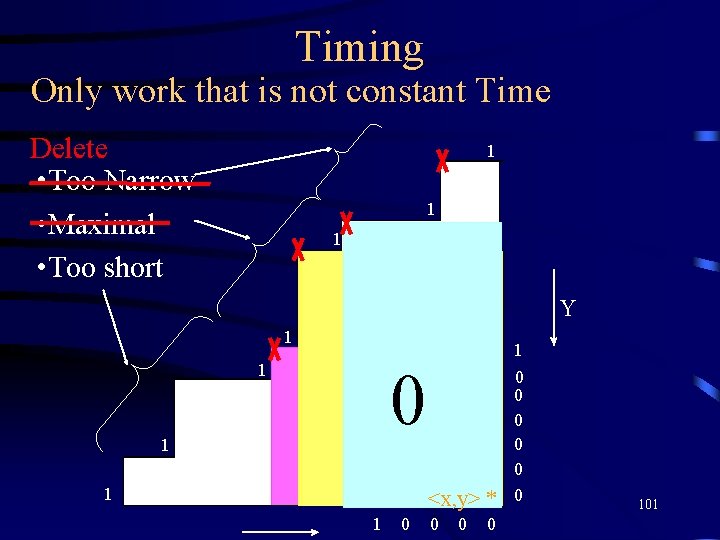
Constructing Maximal Rectangles • Too Narrow • Maximal • Too short <x, y> * 94

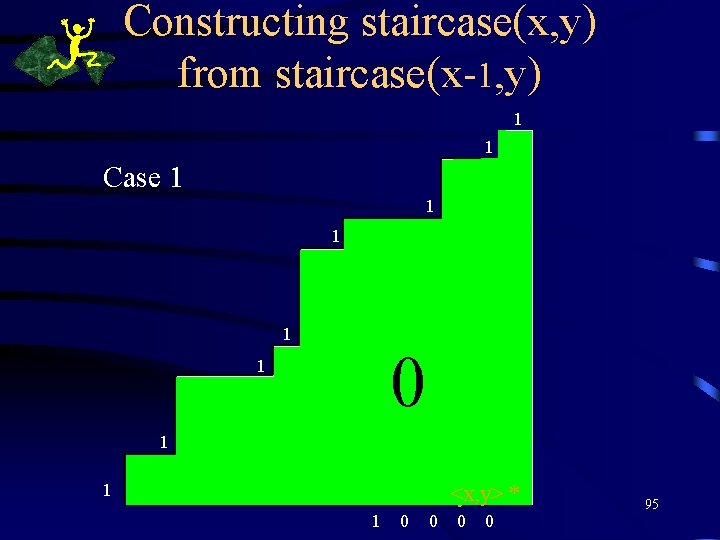
Constructing staircase(x, y) from staircase(x-1, y) 1 1 Case 1 1 0 1 1 1 <x-1<x, y> * 1 0 0 0 0 0 *0 95

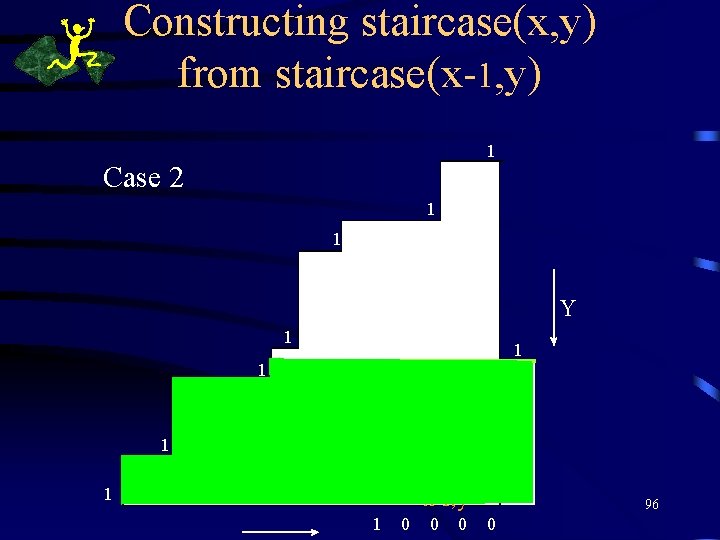
Constructing staircase(x, y) from staircase(x-1, y) 1 Case 2 ( xr , yr ) 1 1 Y 1 1 0 1 ( x 1 , y 1) 1 ( x, y ) <x-1, y> * 1 0 0 0 0 0 96

Constructing staircase(x, y) from staircase(x-1, y) Delete • Too Narrow • Maximal • Too short Keep 1 ( xr , yr ) 1 1 Y 1 00 1 1 0 0 0 ( x, y ) 0 <x, y> <x-1, y> * * 1 ( x 1 , y 1) 1 1 0 0 0 97

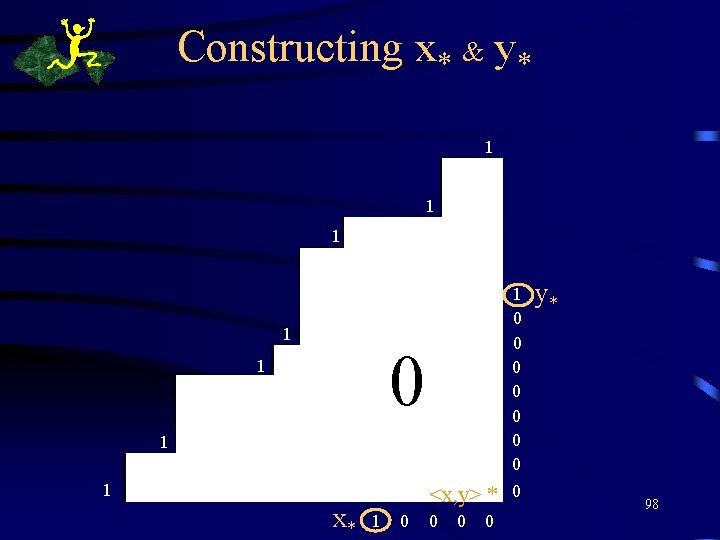
Constructing x* & y* 1 ( xr , yr ) 1 1 1 0 1 ( x 1 , y 1) 1 x* ( x, y ) <x, y> * 1 0 0 0 y* 98

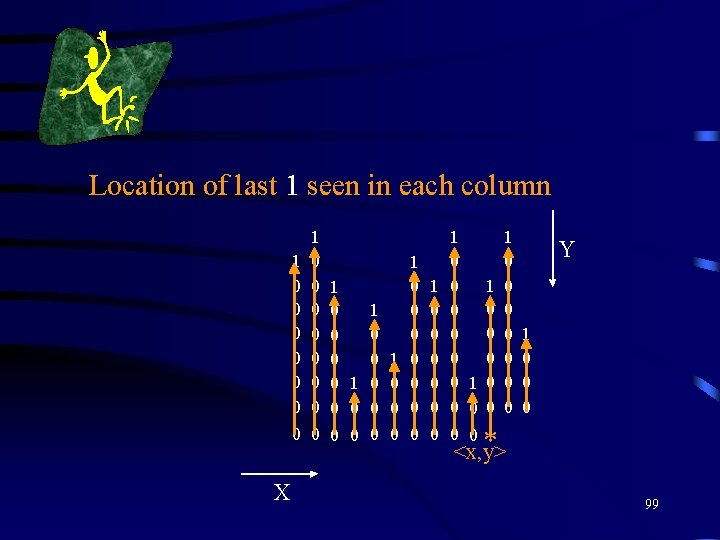
Location of last 1 seen in each column 1 0 0 0 0 X 1 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 Y 1 0 0 0 * <x, y> 99

Structure of Algorithm loop y = 1. . |Y| loop x = 1. . |X| • Construct staircase(x, y) • Output all maximal 0 -rectangles with <x, y> as bottom-right corner 1 YX Third 1 1 0 • 0 1 <x, y> * 1 1 <x. y> Timing O(1) amortized time per <x, y> 100

Timing Only work that is not constant Time Delete • Too Narrow • Maximal • Too short 1 ( xr , yr ) 1 1 Y 1 00 1 1 ( x 1 , y 1) 1 1 0 ( x, y ) <x, y> * 1 0 0 0 0 0 101

Timing Amortized # of steps deleted (per <x, y>) = # of steps created (per <x, y>) £ 1 1 1 0 1 1 1 <x-1, y> * 1 0 0 0 0 0 102

Number of Maximal Rectangles £ # of maximal 0 -rectangles: £ • O( (# 1’s)2 ) [Namaad, Hsu, Lee] • Running time of alg = O( #0’s ) 103

Designing an Algorithm Define Problem Define Loop Invariants Define Measure of Progress 79 km to school Define Step Define Exit Condition Maintain Loop Inv Exit Make Progress Initial Conditions Ending Exit 79 km 75 km 0 km Exit 104

End Iterative Algorithms Math Review Recursive Algorithms 105